Win ratio –An intuitive and easy-to-interpret composite outcome in medical studies

Hongyue WANG, Jing PENG, Juila Z. ZHENG, Bokai WANG, Xiang LU, Chongshu CHEN, Xin M. TU,Changyong FENG,2,*

•Biostatistics in psychiatry (37)•

Win ratio –An intuitive and easy-to-interpret composite outcome in medical studies

Hongyue WANG1, Jing PENG1, Juila Z. ZHENG3, Bokai WANG1, Xiang LU1, Chongshu CHEN1, Xin M. TU4,Changyong FENG1,2,*

time-to-event data; survival functions; proportional hazards model

1. Introduction

Multiple outcomes are quite common in clinical and observational studies as it is difficult to use a single outcome to characterize treatment (exposure) effects.Another reason is that the complexity of a disease may be not adequately characterized by a single outcome.For example, in the study of depression in psychiatric studies, the outcomes may include (i) depression severity such as the Hamilton Depression Rating Scale[1]; (ii) instrumental role functioning such as the Social Adjustment Rating Scale[2]; (iii) social functioning such as the Short Form 36-Item Health Survey[3]and(iv) depression remission status based on clinical assessment. In heart research[4], outcomes of primary interest may include the time to the first heart failure(from study baseline), to death due to heart disease,and to death due to other reasons.

Most research studies attempt to collect as much information as possible in order to study the disease of interest from multiple aspects to find the optimal treatment. Thus, multiple outcomes are usually considered to study treatment effects. However,multiple outcomes impose challenges in data analysis as well as interpretations of study results:

(i) the multiple outcomes in the same study may have different scales. For example, in psychiatric studies, depression status is categorical, while depression severity and social functioning may be continuous (or treated as such if the scale has a wide range). It is difficult to use a multivariate distribution for this kind of mixed outcomes; and

(ii) directions of treatment effects may be different for different outcomes. For example, treatment for depression may reduce depression severity and improve daily living, but may also reduce sexual desires for depressed patients.

A composite outcome is a single outcome based on combinations of multiple study outcomes and is widely used to summarize information from the multiple outcomes. The Intelligence Quotient (IQ) test is an example of a composite outcome, as the test result is a weighted score from four subscales: verbal compression, perceptual reasoning, working memory,and processing speed.[5-6]Composite outcome is also widely used in clinical and observational studies.Overweight or obese people are generally at higher risks for many diseases such as diabetes, hypertension,and heart disease. One widely used measure for obesity is the Body Mass Index (BMI)[7]which is defined as

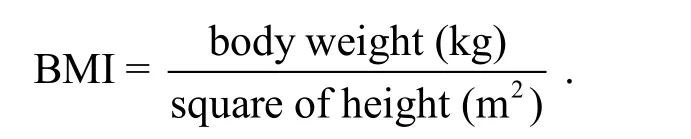
The validity of this index has been widely discussed in literature.[8]

In heart research, patients may experience both heart failures and death, which are two different types of events.[4,9]A treatment may decrease the risks of both types of events or may decrease the risk of one, and increase the risk of the other. How to measure treatment effect is a challenging problem for both physicians and statisticians. One popular practice in heart research is to define a composite outcome, for example,[4]the time to heart failure or death, whichever occurs first. Some well-established methods, such as the Kaplan-Meir estimator[10]and the Cox proportional hazards model[11],can be readily used to analyze such composite outcomes.

The advantages and the disadvantages of composite outcomes have been discussed extensively in the medical literature.[12-41]Heddle and Cook[41]summarize the advantages and disadvantages of using composite outcomes in clinical studies. They also give some guidelines on how to select composite outcomes.The decision to use composite outcome may be debated forever.

In this report note, we review a relatively new method – win ratio- to analyze some types of multiple outcomes in clinical studies. In Section 2 we give a brief introduction to win ratio and statistical properties. Section 3 focuses on the interpretation of this parameter, the population win ratio. Section 4 reports simulation results of estimating win ratio if both the marginal survival functions of the fatal event and the conditional survival functions of the nonfatal event satisfies being in the Lehmman family,[42]followed by conclusion and discussion in Section 5.

2. A brief introduction to win ratio method

Finkelstein and Schoenfeld[43]first develop a nonparametric test, which will be referred to as the FS rank test below, to combine time-to-event and longitudinal outcomes in clinical studies. In this method, each pair chosen from the treatment and control group are compared based on these two types of outcomes. First, subjects are compared based on the time-to-event outcome. If the individual in the treatment group has a longer (shorter) time to event,the treatment group is said to win (lose) in this pair.If for some reason (for example, censoring), their times to event cannot be compared, the longitudinal outcomes will be compared and the win or loss will be determined similarly. The FS rank test is the difference between the numbers of wins and losses in the treatment group. The FR rank test is a generalization of the Wilcoxon rank sum test.

The idea of FS rank test was later expanded by Pocock and colleagues[44]in a clinical trial with two types of events: fatal event (cardiovascular death) and non-fatal event (heart failure hospitalization). Fatal event is assumed to have a higher priority than the non-fatal event when evaluating treatment effects. For each pair of patients, we first determine which patient lives longer than the other. If this is unknown, we then determine who has a better non-fatal event. This is the same idea as the FS rank test. The ratio of the wins over losses in the treatment group is called the win ratio. The treatment is beneficial compared to the control if the win ratio is greater than 1.

Pocock and colleagues[44]offered two approaches to calculating the sample win ratio:

(1) Match pair approach: This is a three-step method to calculating the win ratio statistic.

i. Use a risk score or risk stratification to select matched pairs of patients from treatment and control group.

ii. For each matched pair, one first compares the priority event (e.g., fatal event). If the comparison cannot be made (e.g., which patient dies first),then check the second priority event (e.g., time to hospitalization). There are 5 possible results based on these two comparisons:

(a) patient in the treatment group dies first;

(b) patient in the control group dies first;

(c) if not (a) or (b), patient in the treatment group is hospitalized first;

(d) if not (a) or (b), patient in the control group is hospitalized first;

(e) none of the above.

iii. The comparison results are summarized by Na, Nb,

Nc, Nd, and Ne, corresponding to the numbers of matched pairs in (a), (b), (c), (d), and (e).

The numbers of known wins and losses in the treatment group are Nw=Nb+ Ndand Nl=Na+ Nc. The sample win ratio is

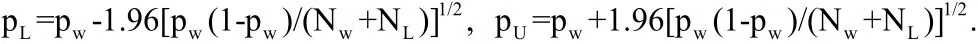
(2) Unmatched pair approach: Analogous to the matched pairs approach, the unmatched pairs approach classifies the comparison results into five categories. The difference is that we compare every subject in the treatment group with every subject in the control group. Let Nnand Nsbe the number of patients in the treatment and control group, we need to make Nn×Nscomparisons.

In the unmatched pair approach, calculating the 95% CI and p-value for Rware quite complex.Finkelstein & Schoenfeld[43]described the general idea of significance test. Two-sample U- statistic theory provides expressions for the asymptotic variance of the win-ratio statistic for unmatched pairs. Luo and colleagues[45]derive an alternative standard error estimate using counting process methods.

3. The mathematical meaning of win ratio

Recently, Oakes[46]extended the win ratio statistic to define the probability win ratio, the ratio of the win and loss probabilities, for general survival models when follow-up of all patients is over a specified time interval[0, c]. This extension not only avoids the complex subjecting matching process (or comparisons of all subjects between the treatment and control group), but also gives rise to nice statistical properties.

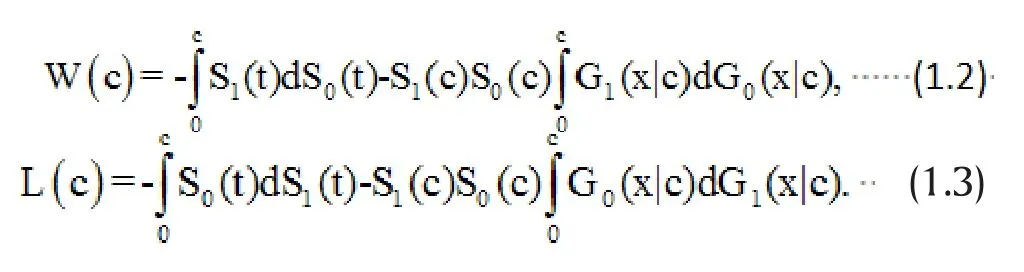
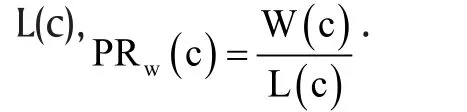
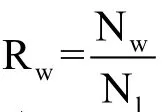
It is clear that the win ratio defined above depends on the specified observation window [0, c]. This means that for the same study, if we stop the study at different follow-up times, we will be estimating different win ratio parameters,PRw(c ). In the extreme case, if c is sufficiently large, deaths censored by the observation window will be negligibly small and the second priority event may become irrelevant. In general,P Rw(c)is a function of c. However, as shown in Oakes,[46]the win ratio will be independent of the observation time c if the marginal survival function and conditional survival function are both in the Lehmann family sharing the same parameters. Moreover, this shared parameter has the interpretation of both the hazard ratio and loss ratio (the reciprocal of the win ratio). This is quite a nice statistical property as the hazard ratio is widely used to measure treatment effects under the popular Cox proportional hazards model.

4. A small simulation study

We now discuss how to estimate the probability win ratio under the assumption that both the marginal and conditional survival functions are in the Lehmann family with the same parameters. We also show how to use the Wei-Lin-Weissfeld[47]method to obtain a more efficient estimator by combining the estimators obtained from fatal and non-fatal events separately.

In the control group, we assume the joint survival function of (T, X) is

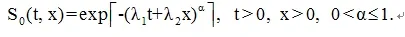
For the treatment group we assume the joint survival function of (T, X) is

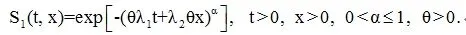
The correlation of T and X is described by α; T and X become highly if α is close to 0 and independent when α=1. Under the above specifications, the win ratio parameter in the absence of censoring is PRw=1/θα. We also assume that both the fatal and non-fatal events are subject to independent censoring with the censoring time C exponentially distributed with a rate q.

We first used the Cox proportional hazards model to estimate the win ratio based on (1) the non-fatal event, where the non-fatal event time may be censored by either the censoring time C or the fatal event time;(2) fatal event, where the time may be censored by the censoring time C. The Wei-Lin-Weissfeld[47]method was used to combine these two estimators.

Table 1 reports the results after 1,000 Monte Carlo simulations based on sample size n=2,000(λ1=0.1,λ2=0.6, θ=0.5, and q=0.5). With such a large sample size, both estimates from fatal events and non-fatal events should be close to the true win ratio parameter.The estimates obtained from the Wei-Lin-Weissfeld[48]combination method is always more efficient than the other two methods, especially when the correlation between the fatal and non-fatal event is weak (large α).

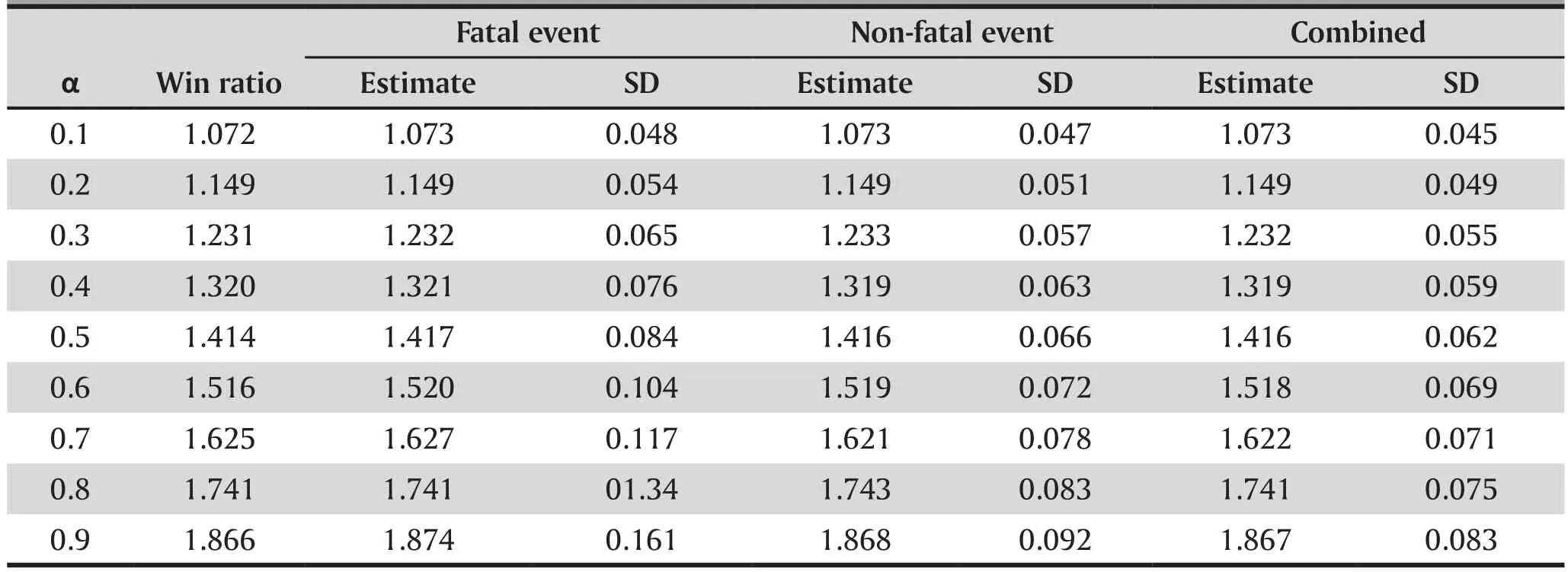
Table 1. Estimate of win ratio

5. Conclusion and Future work

In medical studies with multiple outcomes, it is often difficult to construct appropriate composite outcomes to evaluate treatment effects that reflect the multifaceted nature of interventions. In this paper we review the concept of win ratio and associated methods to facilitate such a difficult process. The win ratio is an intuitive and easy-to-interpret composite outcome and is readily implemented within the context of survival analysis, especially with the probability win ratio.

Since win ratio is new, more work is needed to study its properties and applications. We propose two future research areas in win ratio analysis:

(1) In most clinical or observational studies, we want to estimate the treatment effects after adjusting the confounding effects of other covariates. How to incorporate the estimation of win ratio in semiparametric regression analysis is a new area to be explored.

(2) Power analysis based on win ratio. In the clinical study design, the sample size calculation is usually based on the proposed treatment effects. How to calculate the sample size given the proposed win ratio is another research topic.

Funding

Not available.

Conflict of interest statement

The authors report no conflict of interest

Authors’ contribution

Hongyue Wang, Xin M. Tu, and Changyong Feng:manuscript drafting.

Julia Z. Zheng and Bokai Wang: literature review

Jing Peng, Xiang Lu, and Chongshu Chen: simulation studies

1. Hamilton M. A rating scale for depression. J Neurol Neurosurg Psychiatry. 1960; 23: 56-62

2. Holmes TH, Rahe RH. The Social Readjustment Rating Scale.J Psychosom Res. 1967; 11(2): 213–218

3. Ware JE, Sherbourne CD. The MOS 36-Item Short-Form Health Survey (SF-36): I. Conceptual framework and item selection. Med Care. 1992; 30: 473-483.

4. Moss AJ, Hall WJ, Cannom DS, Klein H, Brown MW,Daubert JP, et al. Cardiac-resynchronization therapy for the prevention of heart-failure events. N Engl J Med.2009; 361(14):1329-1338. doi: http://dx.doi.org/10.1056/NEJMoa0906431

5. Gozali J, Meyen EL. The influence of the teacher expectancy phenomenon on the academic performances of educable mentally retarded pupils in special classes. J Spec Educ. 1970; 4: 417-424. doi: https://doi.org/10.1177/002246697000400406

6. Hauser-Cram P, Sirin SR, Stipek D. When teachers’ and parents’ values differ: Teachers’ ratings of academic competence in children from low-income families. J Educ Psychol. 2003; 95(4): 813-820. doi: http://dx.doi.org/10.1037/0022-0663.95.4.813

7. Keys A, Fidanza F, Karvonen MJ, Kimura N, Taylor HL. Indices of relative weight and obesity. J Chronic Dis. 1972; 25(6):329-343

8. Campos P, Saguy A, Ernsberger P, Oliver E, Gaesser G. The epidemiology of overweight and obesity: Public health crisis or moral panic? Int J Epidemiol. 2006; 35(1): 55-60. doi:http://dx.doi.org/10.1093/ije/dyi254

9. Lim E, Brown A, Helmy A, Mussa S, Altman DG. Composite outcomes in cardiovascular research: a survey of randomized trials. Ann Intern Med. 2008; 149(9): 612-617

10. Kaplan EL, Meier P. Nonparametric estimation from incomplete observations. J Amer Statist Assn. 1958; 53(282):457–481

11. Cox DR. Regression Models and Life-Tables (with discussion).J R Stat Soc Series B. 1972; 34(2): 187–220

12. Freemantle N, Calvert M, Wood J, Eastaugh J, Griffin C.Composite outcomes in randomized trials: greater precision but with greater uncertainty? JAMA. 2003; 289(19): 2554-2559. doi: http://dx.doi.org/10.1001/jama.289.19.2554

13. Neaton JD, Gray G, Zuckerman BD, Konstam MA. Key issues in end point selection for heart failure trials: Composite end points. J Card Fail. 2005; 11(8): 567-575. doi: http://dx.doi.org/10.1016/j.cardfail.2005.08.350

14. Montori VM, Permanyer-Miralda G, Ferreira-González I,Busse JW, Pacheco-Huergo V, Bryant D, et al. Validity of composite end points in clinical trials. BMJ. 2005; 330(7491):594-596. doi: http://dx.doi.org/10.1136/bmj.330.7491.594

15. Freemantle N, Calvert M. Weighing the pros and cons for composite outcomes in clinical trials. J Clin Epidemiol.2007; 60(7): 658-659. doi: http://dx.doi.org/10.1016/j.jclinepi.2006.10.024

16. Ferreira-González I, Permanyer-Miralda G, Busse JW,Bryant DM, Montori VM, Alonso-Coello P, et al. Composite endpoints in clinical trials: the trees and the forest. J Clin Epidemiol. 2007; 60(7): 660-661. doi: http://dx.doi.org/10.1016/j.jclinepi.2006.10.021

17. Freemantle N, Calvert M. Composite outcomes - final comment for now. J Clin Epidemiol. 2007; 60(7): 662 - 662.doi: http://dx.doi.org/10.1016/j.jclinepi.2006.12.005

18. Lim E, Brown A, Helmy A, Mussa S, Altman DG. Composite outcomes in cardiovascular research: a survey of randomized trials. Ann Intern Med. 2008; 149(9): 612-617

19. Mell LK, Jeong JH. Pitfalls of using composite primary end points in the presence of competing risks. J Clin Oncol.2010; 28(28): 4297-4299. doi: http://dx.doi.org/10.1200/JCO.2010.30.2802

20. Ferreira-González I, Busse JW, Heels-Ansdell D, Montori VM,Akl EA, Bryant DM, et al. Problems with use of composite end points in cardiovascular trials: systematic review of randomised controlled trials. BMJ. 2007; 334: 786. doi:http://dx.doi.org/10.1136/bmj.39136.682083.AE

21. Cannon CP. Clinical perspectives on the use of composite endpoints. Control Clin Trials. 1997; 18(6): 517-529. doi:http://dx.doi.org/10.1016/S0197-2456(97)00005-6

22. Buzney EA, Kimball AB. A critical assessment of composite and coprimary endpoints: A complex problem. J Am Acad Dermatol. 2008; 59(5): 890-896. doi: http://dx.doi.org/10.1016/j.jaad.2008.05.021

23. Bethel MA, Holman R, Haffner SM, Califf RM, Huntsman-Labed A, Hua TA, et al. Determining the most appropriate components for a composite clinical trial outcome.Am Heart J. 2008; 156(4): 633-640. doi: http://dx.doi.org/10.1016/j.ahj.2008.05.018

24. Pogue J, Devereaux PJ, Thabane L, Yusuf S. Designing and analyzing clinical trials with composite outcomes:consideration of possible treatment differences between the individual outcomes. PLoS One. 2012; 7(4): e34785. doi:http://dx.doi.org/10.1371/journal.pone.0034785

25. Eurich DT, Majumdar SR, McAlister FA, Tsuyuki RT,Yasui Y, Johnson JA. Analyzing composite outcomes in cardiovascular studies: traditional Cox proportional hazards versus quality-of-life–adjusted survival approaches. Open Med. 2010; 4(1): e40–e48

26. Teixeira-Pinto A, Siddique J, Gibbons R, Normand SL.Statistical approaches to modeling multiple outcomes in psychiatric studies. Psychiatr Ann. 2009; 39(7): 729–735. doi:http://dx.doi.org/10.3928/00485713-20090625-08

27. Rauch, G, Rauch B, Schüler S, Kieser M. Opportunities and challenges of clinical trials in cardiology using composite primary endpoints. World J Cardiol. 2015; 7(1): 1–5. doi:http://dx.doi.org/10.4330/wjc.v7.i1.1

28. Subherwal S, Anstrom KJ, Jones WS, Felker MG, Misra S, Conte MS, et al. Use of alternative methodologies for evaluation of composite end points in trials of therapies for critical limb ischemia. Am Heart J. 2012; 164(3): 277-284.doi: http://dx.doi.org/10.1016/j.ahj.2012.07.002

29. Lavine KJ, Mann DL. Rethinking phase II clinical trial design in heart failure. Clin Investig (Lond). 2013; 3(1):57-68. doi:http://dx.doi.org/10.4155/cli.12.133

30. Mentz RJ, Felker GM, Ahmad T, Peacock WF, Pitt B, Fiuzat M,et al. Learning from recent trials and shaping the future of acute heart failure trials. Am Heart J. 2013; 166(4): 629-635.doi: http://dx.doi.org/10.1016/j.ahj.2013.08.001

31. Rogers JK, Pocock SJ, McMurray JJ, Granger CB, Michelson EL, Östergren J, et al. Analysing recurrent hospitalizations in heart failure: a review of statistical methodology, with application to CHARM-Preserved. Eur J Heart Fail. 2014;16(1): 33-40. doi: http://dx.doi.org/10.1002/ejhf.29

32. Goldberg R, Gore JM, Barton B, Gurwitz J. Individual and composite study endpoints: separating the wheat from the chaff. Am J Med. 2014; 127(5): 379-384. doi: http://dx.doi.org/10.1016/j.amjmed.2014.01.011

33. Prakash R, Horsfall M, Markwick A, Pumar M, Lee L,Sinhal A, et al. Prognostic impact of moderate or severe mitral regurgitation (MR) irrespective of concomitant comorbidities: A retrospective matched cohort study. BMJ Open. 2014; 4(7): e004984. doi: http://dx.doi.org/10.1136/bmjopen-2014-004984

34. Khawaja MZ, Wang D, Pocock S, Redwood SR, Thomas MR.The percutaneous coronary intervention prior to transcatheter aortic valve implantation (ACTIVATION) trial:study protocol for a randomized controlled trial. Trials 2014;15: 300. doi: http://dx.doi.org/10.1186/1745-6215-15-300

35. Ensor JE. Biomarker validation: common data analysis concerns. Oncologist. 2014; 19(8): 886-891. doi: http://dx.doi.org/10.1634/theoncologist.2014-0061

36. Senni M, Paulus WJ, Gavazzi A, Fraser AG, Díez J, Solomon SD, et al. New strategies for heart failure with preserved ejection fraction: the importance of targeted therapies for heart failure phenotypes. Eur Heart J. 2014; 35(40): 2797-2815. doi: http://dx.doi.org/10.1093/eurheartj/ehu204

37. Claggett B, Tian L, Castagno D, Wei LJ. Treatment selections using risk-benefit profiles based on data from comparative randomized clinical trials with multiple endpoints.Biostatistics. 2015; 16(1): 60-72. doi: http://dx.doi.org/10.1093/biostatistics/kxu037

38. Lachin JM, Bebu I. Application of the Wei-Lachin multivariate one-directional test to multiple event-time outcomes. Clin Trials. 2015; 12(6): 627-633. doi: http://dx.doi.org/10.1177/1740774515601027

39. Bebu I, Lachin JM. Large sample inference for a win ratio analysis of a composite outcome based on prioritized components. Biostatistics. 2016; 17(1): 178-187. doi: http://dx.doi.org/10.1093/biostatistics/kxv032

40. Evans SR, Pennello G, Pantoja-Galicia N, Jiang H, Hujer AM,Hujer KM, et al.Benefit-risk Evaluation for Diagnostics: A Framework (BED-FRAME). Clin Infect Dis. 2016; 63(6): 812-817. doi: http://dx.doi.org/10.1093/cid/ciw329

41. Heddle NM, Cook RJ. Composite outcomes in clinical trials:what are they and when should they be used? Transfusion.2011; 51: 11-13. doi: http://dx.doi.org/10.1111/j.1537-2995.2010.02930.x

42. Lehmann EL. Ordered families of distributions. Ann Math Stat. 1955; 26(3): 399-419. doi: http://dx.doi.org/10.1214/aoms/1177728487

43. Finkelstein DM, Schoenfeld DA. Combining mortality and longitudinal measures in clinical trials. Stat Med. 1999;18(11): 1341-1354

44. Pocock SJ, Ariti CA, Collier TJ, Wang D. The win ratio: a new approach to the analysis of composite endpoints in clinical trials based on clinical priorities. Eur Heart J. 2012; 33(2):176-182. doi: http://dx.doi.org/10.1093/eurheartj/ehr352

45. Luo X, Tian H, Mohanty S, Tsai WY. An alternative approach to confidence interval estimation for the win ratio statistic. Biometrics. 2015; 71(1): 139-145. doi: http://dx.doi.org/10.1111/biom.12225

46. Oakes D. On the win-ratio statistic in clinical trials with multiple types of event. Biometrika. 2016; 103(3): 742-745.doi: http://dx.doi.org/10.1093/biomet/asw026

47. Wei LJ, Lin DY, Weissfeld L. Regression analysis of multivariate incomplete failure time data by modeling marginal distributions. J Am Stat Assoc. 1989; 84: 1065-1073

赢率-医学研究中一个直观而易于解释的综合结果

Wang H, Peng J, Zheng J Z, Wang B, Lu X, Chen C, Tu XM, Feng C

时间-事件数据；生存函数；比例风险模型

Summary:In medical studies with multiple outcomes, researchers always need to make choices as to whether to use a composite outcome (after combining multiple outcomes) as their primary outcome. In this paper we review a new measurement of the treatment effect – win ratio, which can be easily used in studies with prioritized multiple outcomes. We also propose some research topics to be done in this area.

[Shanghai Arch Psychiatry. 2017; 29(1): 55-60.

http://dx.doi.org/10.11919/j.issn.1002-0829.217011]

1Department of Biostatistics and Computational Biology, University of Rochester, Rochester, NY, USA

2Department of Anesthesiology, University of Rochester, Rochester, NY, USA

3Department of Microbiology and Immunology, McGill University, Montreal, QC, Canada

4Department of Family Medicine and Public Health, UC San Diego School of Medicine, La Jolla, CA, USA

*correspondence: Dr. Changyong Feng. Mailing address: Department of Biostatistics and Computational Biology, University of Rochester, 601 Elmwood Avenue, Rochester, NY, USA. Postcode: NY. 14642. E-Mail: Changyong_feng@urmc.rochester.edu

概述：对于医学研究中的多个结果，研究人员总是需要选择是否使用一个综合性结果（综合多个结果后所得的）作为主要结果。在本文中，我们回顾了治疗效果的一个新测量方式-赢率，它可以很容易地用于具有多个优先级结果的研究中。并且，我们在这块领域也提出了一些研究课题。

Dr. Hongyue Wang obtained her BS in Scientific English from the University of Science and Technology of China (USTC) in 1995, and PhD in Statistics from the University of Rochester in 2007. She is a Research Associate Professor in the Department of Biostatistics and Computational Biology at the University of Rochester Medical Center. Her research interests include longitudinal data analysis, missing data, survival data analysis, and design and analysis of clinical trials. She has extensive and successful collaboration with investigators from various areas, including Infectious Disease, Nephrology, Neonatology, Cardiology,Neurodevelopmental and Behavioral Science, Radiation Oncology, Pediatric Surgery, and Dentistry. She has published more than 70 statistical methodology and collaborative research papers in peer-reviewed journals.