以滞量为参数的广义Lienard方程的数值逼近

初颖，吕堂红

（长春理工大学 理学院，长春 130022）

以滞量为参数的广义Lienard方程的数值逼近

初颖，吕堂红

（长春理工大学 理学院，长春 130022）

利用欧拉方法研究了对以滞量为参数的具有Hopf分支的广义Lienard方程的数值逼近问题。首先，利用欧拉方法将得到的时滞差分方程表示为映射，然后以时滞r为分支参数，利用离散动力系统的分支理论，在广义Lienard方程具有Hopf分支的条件下，给出了差分方程Hopf分支存在的条件，及连续系统与其数值逼近间的关系，证明了当该系统在r=r0产生Hopf分支时，其数值逼近也在相应的参数rh处具有Hopf分支，并且rh=r0+o(h)，最后给出了一个数值仿真的例子，仿真结果表明Euler离散后的系统依旧保持了原系统的动力学性质，从而验证了理论结果的正确性.

广义Lienard方程；欧拉方法；Hopf分支；数值逼近

近年来，广义Lienard方程解的型态受到许多学者的关注。而滞量是引起时滞微分方程和常微分方程差异的关键，因而，以滞量为参数研究Hopf分支问题是很有意义的。

关于系统（1）的Hopf分支问题，已经有很多学者做了深入研究［1-3］。例如，1998年，文献［1］以时滞r为参数研究了系统（1）的Hopf分支问题，证明了Hopf分支的存在性，同时给出了计算Hopf分支的公式；文献［2］利用指数多项式的τ-D划分法讨论了系统（1）的以k为分支参数的Hopf分支问题；而文献［3］则以参数b讨论了系统（1）的Hopf分支情况，并给出了在r-b参数平面上的Hopf分支图。

本文将利用欧拉方法，以滞量r为分支参数继续讨论系统（1）的Hopf分支的数值逼近问题。文献［4-7］率先开始了对时滞Logistic方程Hopf分支的数值逼近问题的研究，并得到了一系列令人满意的结果。所谓“数值逼近”，就是研究当用数值方法对系统进行离散化时，考察其数值解能否保持该系统的动态特性的问题。

1 广义Lienard方程的Hopf分支的存在性

对于系统（1），假设时滞r＞0为常数，f,g∈C2,并且g(x)满足g(0)=0，xg(x)＞0。

记f(0)=a，g′(0)=b,并且a＞0,b＞0。

系统（1）等价于下面的二阶时滞系统：

记̇=y，再作时间变换t=rs，并将x(rs),y(rs)仍记为x(t),y(t)，则（2）化为其等价系统：

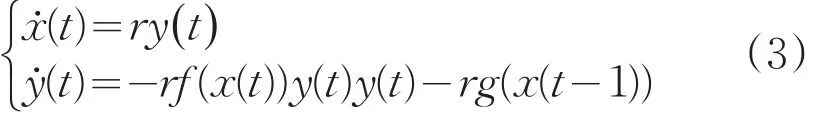
其中，线性部分为：

（4）的特征方程为：

引理1 设r为参数，则当r=r0时，方程（3）有Hoof分支，其中r0满足以下条件：

（i）方程（5）有一对共轭复根λ1,2=α(r)±iβ(r)，此处α,β是实数，且α(r0)=0，β(r0)=ω0＞0；

（ii）方程（5）在r=r0时的根，除λ(r0),λˉ(r0)外其余根都具有严格负实部；

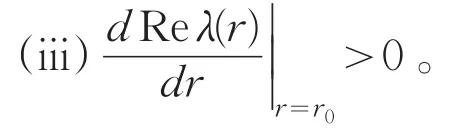
2 广义Lienard方程的Hopf分支的数值逼近

引入新向量Xn=(xn,yn,xn-1,yn-1,…,xn-m,yn-m)T，将（7）表示为

其中，F(x)=(F0,F1,…,Fm)T是一个2(m+1)维的向量值函数，即：

将（8）式在（0，0）处展开，

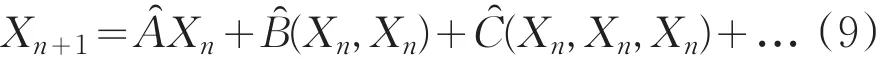
其线性部分为：

其中，

I为二阶单位阵，

的特征方程为：

为了方便讨论方程（3）的数值解的分支问题，引入下面方程：

类似于文献［8］中的引理4.1，有引理2。

引理2 若特征方程（5）满足条件（6），则D(μ,r,h)=0满足：

（i）D(μ,r,h)=0 有一对共轭复根μ1,2=σ(r)±iω(r)；

（ii）存在rh满足rh=r0+o(h)，σ(rh)=0,ω(rh)≠0 ；

证 明 ：（i-iii） 由 于D(μ,r,0)=d(μ,r) ，故D(iω0,r,0)=d(iω0,r). 在 (iω0,r0,0) 处

故dμ(iω0,r0)≠0.由隐函数存在定理，在 (r0,0)邻域内存在唯一函数σ(r,h),ω(r,h)使得μ1,2=

（iv）令 {μm},rm,hm使 得D(μm,rm,hm)=0,(rm,hm)∈N(r0,0),那么 |μm|一致有界。从而存在mj，使得μmj→μ0，rmj→r0，hmj→0。由D(μ0,r0,0)=0的连续性，有μ0=iω0,rh=r0。故：

从而引理3得证。

定理1 若微分方程（3）在r=r0处有Hopf分支，则当步长h充分小时，差分方程（8）在rh=r0+o(h)处也产生Hopf分支。

3 数值模拟

本小节对系统（1）给出了一个数值仿真的例子。仿真结果表明Euler离散后的系统依旧保持了原系统的动力学性质，从而验证了理论结果的正确性。

令f′(0)=a1=0.8，g′(0)=b=1.则系统（1）变为：

此时系统（13）存在唯一平衡点E*=(0,0).由文献［3］的定理4.1易计算：r0≈0.378 316 029 857 13,于是，系统（13）在r=r0处产生Hopf分支。

图1 当r=0.2＜r0时，系统（13）的相图和波图

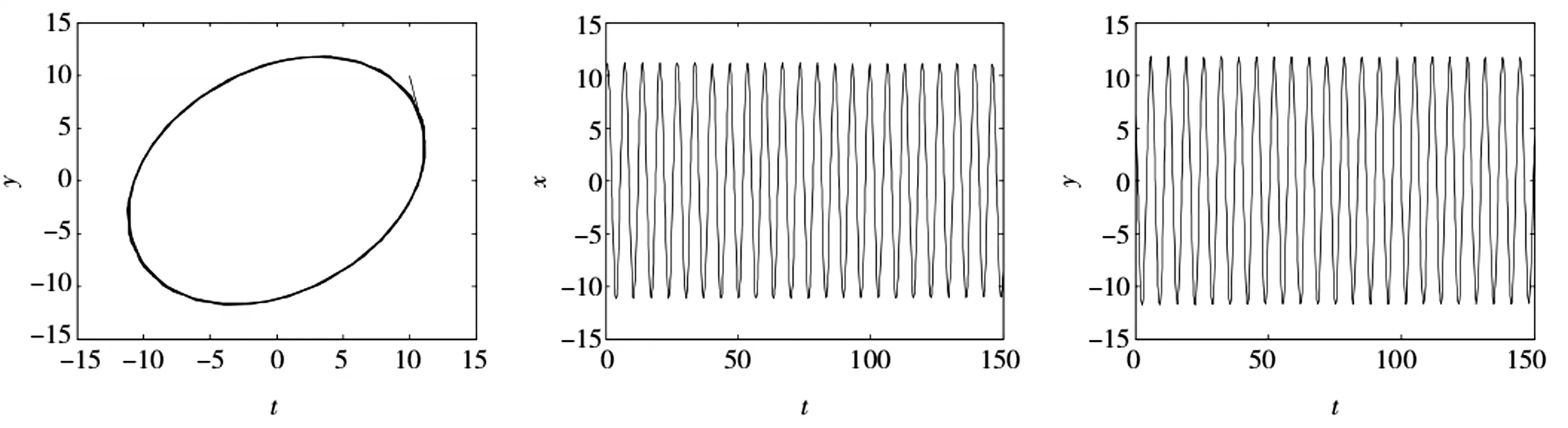
图2 当r=r0时，系统（13）的相图和波图

图3 当r=0.55＞r0时，系统（13）的相图和波图

图4 当r=0.2＜r0,h=0.02时，离散系统（8）的相图和波图

图5 当r=r0,h=0.02时，离散系统（8）的相图和波图

图6 当r=0.55＞r0,h=0.02时，系统（8）的相图和波图

图1-3分别表示未离散前解的系统（13）的波形图及轨线图。图4-6分别表示用Euler法离散后的系统（8）的波形图及轨线图。从图1中可以看出，当r＜r0时系统零解是渐进稳定的，从图2可以看出r=r0时系统在原点处经历Hopf分支，并在平衡点附近有稳定的分支周期解产生，从图3可以看出当r＞r0时系统零解不稳定。由图4-6可知，当r＜r0时，系统（8）零解是渐进稳定的，在r=r0附近时，有稳定周期解产生，当r＞r0时，系统（8）零解不稳定，说明Euler离散后的系统（8）依旧保持了原系统（1）的动力学性质。

［1］唐风军，黄振勋，阮炯.以滞量为参数的广义Lienard方程的Hopf分支［J］.数学年刊，1998，19A：（4）：469-476.

［2］马苏奇，陆启韶.一类具有时滞的Lienard方程的Hopf分支［J］.中国农业大学学报，2003，8（4）：1-4.

［3］唐明.具有限时滞的广义Lienard方程的Hopf分［D］.长春：东北师范大学，2002.

［4］Lambert J D.Numerical method for ordinary differential equations［M］.Chichester：John Wiley，1991.

［5］Kazarino N，Wan Y H，Van den Driessche P.Hopf bifurcation and stability of periodic solutions of differential-difference and integro-differential equations［J］.Journal of the Institute of Mathematical Appliations，1978（21）：461-467.

［6］Halej，Lunel S V.Introduction to functional differential equations［M］.New York：Spring-Verlag，1993.

［7］Guckenheimer J，Holmes P J.No linear oscillations，dynamical systems and bifurcation of vector fields［M］.New York：Spring-Verlag，1983.

［8］Neville Ford，Volker Wulf.Numerical Hopf bifurcation for a class of delay differential equations［J］.JCAM，2000（115）：601-616.

Numerical Approximation of Generalized Lienard Equation with Delay As a Parameter

CHU Ying，LV Tanghong
（School of Science，Changchun University of Science and Technology，Changchun 130022）

The numerical approximation of the generalized Lienard equation which has Hopf bifurcations and with delay as parameter is considerd by using Euler method.Firstly，the delay deference equation obtained by using Euler method is written as a mapping.Then，under the condition that the generalized Lienard equation has Hopf bifurcation，by taking time delay ras the bifurcation parameter and using the bifurcation theory of discrete dynamical systems，we give the conditions for the existence of Hopf bifurcation of difference equations and the relationship between continuous system and numerical approximation of the continuous system，furthermore，we proved that the numerical approximation also has Hopf bifurcations at corresponding parametersrhand rh=r0+o(h)when the system has Hopf bifurcations atr=r0.Finally，an example of numerical simulation is given，the simulation results show that the system which is discretized by Euler till keeps the dynamical property of the original system，which verifies the correctness of the theoretical results.

the generalized Lienard equation；Euler method；Hopf bifurcation；numerical approximation

O175

A

1672-9870（2017）05-0128-04

2017-09-29

国家自然科学基金（10726062）

初颖（1984-），女，博士，讲师，E-mail：chuying_12345@sina.com

吕堂红（1979-），女，副教授，E-mail：lvtanghong@163.com