基于聚类布尔矩阵的Apriori算法的研究

田磊，崔广才，何旭，陈建新

（长春理工大学 计算机科学技术学院，长春 130022）

基于聚类布尔矩阵的Apriori算法的研究

田磊，崔广才，何旭，陈建新

（长春理工大学 计算机科学技术学院，长春 130022）

针对聚类布尔矩阵的Apriori算法—CBM_Apriori算法的不足之处，提出了一种基于聚类布尔矩阵的Eclat算法—CBM_Eclat算法。该算法首先对布尔矩阵使用K-medoids算法，获得权值和聚类后的布尔矩阵；然后将聚类后的布尔矩阵转换成Tidset，并采用逻辑“交操作”运算，进而有效地减少了聚类布尔矩阵存储和候选项集的生成，提高了该算法的执行效率。通过实例应用和算法执行结果都能够证明CBM_Eclat算法具有可行性和有效性。

CBM_Apriori算法；CBM_Eclat算法；布尔矩阵；K-medoids算法；Tidset

关联规则最常见的算法是Apriori算法［1］和FP-Growth算法［2］，它们都是水平数据表示法［3］挖掘频繁项集，但是这两种算法都有着自己的缺陷，Apriori算法的缺陷是反复扫描事务数据库和产生大量的候选项集，而FP-Growth算法的缺陷是占用大量的内存空间。于是，研究者们对它们的缺陷进行了大量的研究，提出了许多改进的方法，从而提高了算法的运行效率以及减少了存储空间。

本文是针对聚类布尔矩阵的Apriori算法—CBM_Apriori算法［4］，该算法只需要扫描事务数据库一次，但是，还会产生大量的候选项集。于是，本文对该缺点进行改进，对事务数据库使用垂直数据表示方法［5-6］，提出了一种基于聚类布尔矩阵的Eclat算法—CBM_Eclat算法，该算法也仅需要扫描事务数据库一次即可，减少了候选项集的生成，从而提高了算法的执行效率。

1 基本概念

1.1 布尔矩阵

布尔矩阵［7］具有矩阵所有的运算性质，如与/交操作运算。其基本思想为：首先对事务数据库D进行扫描并转换成布尔矩阵形式，即为Dmn=(dij)mn，其中：

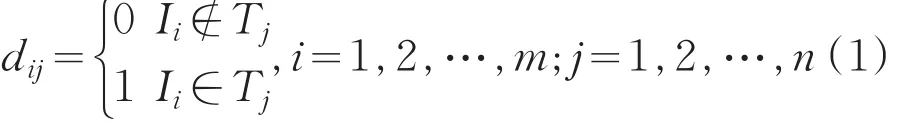
事务数据库D中的项和事务分别用行向量和列向量表示，即行向量表示成项，列向量表示事务。如果第j个事务中有第i个项，则矩阵对应第i行和第j列的数值为1，否则数值为0。

1.2 水平和垂直数据表示

经典的Apriori算法和FP-Growth算法都是采用水平数据表示方法，其中事务由事务标识符［8］（TID）和项目［9］（Item）两部分组成。每个事务交易仅有唯一一个TID，而一个TID对应一个项集（Itemsets）由一个项目或者多个项目组成。水平数据表示如表1所示。

Eclat算法［5-6］就是采用垂直数据表示方法，该方法是由事务数据库中的Item和事务交易中每个项目按唯一的TID的数字集合表示记为Tidset组成。垂直数据表示如表2所示。

1.3 支持度计数（sup_count）

关联规则挖掘频繁项集过程中，计算每个项的sup_count是必不可少的，但是，计算sup_count有两种方法［10-11］：一种是计数法，该方法应用水平数据表示的算法中，如Apriori算法。而一种是交集操作法，该方法由于垂直数据表示的算法中，如Eclat算法。即支持度阈值support（sup）如公式（2）所示，而“交操作”运算sup_count如公式（3）所示。

其中，X和Y是Item，T(X)和T(Y)是对应项的Tidset。

1.4 实例应用

某事务数据库中有10个事务，D={T1,T2,…,T10}，对应的项目集I={I1,I2,I3,I4,I5}，如表1所示。假设最小支持度min_sup=30%，则最小支持度计数值min_sup_count=min_sup×|D|=30%×10=3。

2 CBM_Apriori算法

2.1 CBM_Apriori算法基本思想

首先扫描事务数据库D，构造成布尔矩阵Dmn，且每列的权值都为1，然后建立AE权值数组来存放每列的权值，即AE[k]。然后采k-medoids聚类算法，将布尔矩阵中含有相同项目的事务数进行聚类，则该列的权值数加1，即权值含有相同项目的事务数，从而压缩了矩阵，获得新的聚类布尔矩阵Dmn。

扫描聚类布尔矩阵，并且计算所有项目的支持度计数（sup_count），将每行矩阵中列向量数值与对应的AE[k]数组的数值进行相乘，再相加得到每行事务的sup_count。即项目Ii的支持度计数公式为：

如果事务的sup_count小于最小支持度计数值（min_sup_count），则该项无法生成频繁2-项集，即删除该项目对应的行向量，得到频繁1-项集矩阵L1。

对频繁1-项集矩阵L1各行按位采用与操作运算，得到候选1-项集矩阵C1。然后将候选1-项集矩阵C1采用（2）中的公式，获得各行的sup_count，如果sup_count大于或者等于min_sup_count，则存储该行向量，否则删除该行向量，即为频繁2-项集矩阵L2。

分别对频繁2-项集矩阵中的各列求和，再将各列之和与对应权值AE[k]相乘，获得列向量数值column（Ti）与 min_sup_count进行比较，如果大于或者等于min_sup_count，则保留该列向量，否则删除该列向量。即列向量数值公式为：

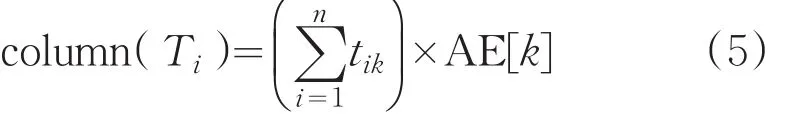
通过列向量数值公式对频繁2-项集矩阵L2进行了压缩，即为压缩频繁2-项集矩阵。

表1 水平数据表示

表2 垂直数据表示

对压缩频繁2-项集矩阵各行按位采用与操作运算，重复进行CBM_Apriori算法的基本思想步骤（3）和（4），生成各频繁K-项集矩阵Lk，即K大于等于3。直到矩阵行数少于或者等于1行时，则算法结束，即所有的频繁项集为L=L1+L2+…+Lk。

2.2 CBM_Apriori算法描述如下：

CBM_Apriori算法的代码如下：

2.3 CBM_Apriori算法的实例应用

事务数据库就是表1。该算法解决步骤如下：

布尔矩阵Dmn进行k-medoids聚类算法生成聚类布尔矩阵D如表3所示。

表3 聚类后的布尔矩阵D

因为事务T1和T10含有相同的项目，则第1列权值为2，其余的权值均为1，I1={100110111}，AE={2，1，1，1，1，1，1，1，1}，sup_count（I1）=1×2+0×1+0×1+1×1+1×1+0×1+1×1+1×1+1×1=7，项目{I1}的sup_count大于或者等于min_sup_count，同理，得到频繁1-项集L1={I1：7，I2：6，I3：7，I4：3，I5：4}。

对频繁1-项集L1，对各行按位采用与操作运算，得到候选1-项集C1，如表4所示。

表4 候选1-项集C1

每行矩阵的列向量的数值乘以对应的权值AE[k]的数值，如I1ΛI2=000110011，AE={2，1，1，1，1，1，1，1，1}，sup_count{I1ΛI2}=0×2+0×1+0×1+1×1+1×1+0×1+0×1+1×1+1×1=4，根据CBM_Apriori算法的基本思想步骤3），项集{I1ΛI2}的sup_count_row大于或者等于min_sup_count，同理，保留各行向量，即得到频繁2-项集L2={I1ΛI2：4，I1ΛI3：5，I1ΛI5：3，I2ΛI3：5，I3ΛI5：4}，如表5所示。

表5 频繁2-项集L2

根据CBM_Apriori算法的基本思想步骤（4），如第一列向量为{01101}，column（T1）=（0+1+1+0+1）×2=6，删除第2、3、5、6、7列以及对应的权值2、3、5、6、7列，获得压缩频繁2-项集矩阵，如表6所示。

对压缩频繁2-项集矩阵，重复进行CBM_Apriori算法的基本思想步骤（5），获得频繁3-项集矩阵L3={I1ΛI2ΛI3：3，I1ΛI3ΛI5：3}，压缩频繁3-项集矩阵，频繁4-项集矩阵L4，如表7所示。

表7 频繁3-项集L3、压缩频繁3-项集矩阵、频繁4-项集L4

（6）直到生成的矩阵的行向量小于或者等于1，结束该算法过程。最后输出矩阵中所有的行向量，即为所有的频繁项集L=L1+L2+L3={I1,I2,I3,I4,I5，I1ΛI2，I1ΛI3，I1ΛI5，I2ΛI3，I3ΛI5，I1ΛI2ΛI3，I1ΛI3ΛI5}。

3 CBM_Apriori算法的改进

为了减少候选项集的生成和存储空间等问题，对CBM_Apriori算法进行改进。本文提出了一种基于聚类布尔矩阵的Eclat算法—CBM_Eclat算法。

3.1 CBM_Eclat算法基本思想

（1）首先扫描事务数据库，构造布尔矩阵D；然后采用k-medoids聚类算法，将布尔矩阵中含有相同项目的事务数进行聚类，从而压缩了布尔矩阵，产生了新的布尔矩阵D1和权值AE[k]；再对新的布尔矩阵D1增加 Tidset，即为T(N)（N=1，2，…，m）。最终得到标记聚类布尔矩阵D2。

（2）对标记聚类布尔矩阵D2进行扫描，寻找该矩阵中每个项目1所对应的T(N)和AE[k]并同时保存；然后计算T(N[Ii])对应的权值AE[k]进行相加为该项的sup_count，如果sup_count大于或者等于min_sup_count，则存储T(N)以及所对应的项和权值AE[k]，否则删除，即获得频繁1-项集L1。

（3）频繁1-项集中每项所对应的T(N)两两采用交操作运算，得到候选项集C1以及对应的T(N)权值AE[k]；然后重复步骤（2），即获得频繁2-项集

L2。

（4）重复步骤（3），直到T(N)不能两两采用交操作运算，则算法结束，即获得所有的频繁项集L。

3.2 CBM_Eclat算法描述

R语言编写CBM_Eclat算法的主要代码如下：

输入：Tidset数据库D，最小支持度计数值min_sup_count；

输出：所有的频繁项集Lk；

（1）对事务数据库进行聚类

①D＜-read.csv（“data.csv”，header=TRUE）

#导入数据集；

②set.seed（0）

#设置随机种子；

③pamx＜-pam（Data，k）

#构造k-medoid聚类模型；

④AE＜-pamx$clusinfo

#获得聚类后权值AE；

⑤D＜-pamx$medoids

#获得聚类后布尔矩阵D；

（2）生成频繁1-项集L1

①扫描标记聚类布尔矩阵D；

②Eclat（D，AE[k]）

③ for each项集i∈I{

④ for each标记符T(N)∈D

⑤i.sup_count=AE［1］+...+AE［n］，

其中，n=1，2，...，N；

#计算项集支持度计数；

⑥ }

⑦L1=（i∈项集 I|i.sup_count＞=min_sup_count）

#大于或者等于支持度计数的候选项集为频繁项集L1；

（3）生成候选项集Ck和频繁项集Lk

3.3 CBM_Eclat算法的实例应用

事务数据库如表1所示。该算法解决步骤如下：

（1）扫描布尔矩阵D，然后对布尔矩阵D进行k-medoids聚类算法生成聚类布尔矩阵 D1和AE[k]，对聚类布尔矩阵D1使用标记T(N)，于是由AE[k]、标记T(N)和聚类布尔矩阵D1构成标记聚类布尔矩阵D2，如表8所示。

表8 标记聚类布尔矩阵D2

（2）根据CBM_Eclat算法，得出Tidset垂直数据库，如表9所示。

计算每个项的T(N)个数为sup_count，如T(N[I1])={1，4，5，7，8，9}，则sup_count（I1）=2+1+1+1+1+1=7，保存大于或者等于min_sup_count的项以及对应的T(N)。故得到频繁1-项集L1={I1:7,I2:6,I3:7,I4:3,I5:4}。

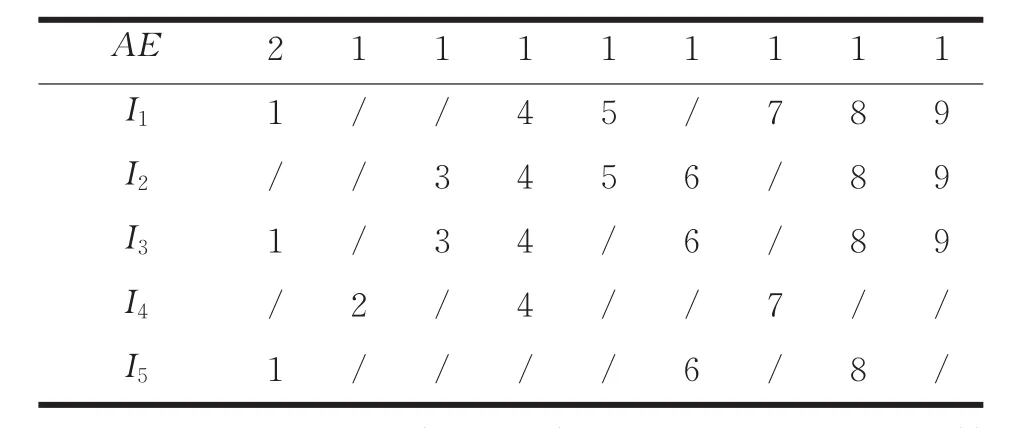
表9 Tidset垂直数据库

（3）对Tidset垂直数据库两两采用交操作运算以及对应AE[k]，获得候选项集C1，如图1所示。

与步骤（2）计算sup_count相同，保存大于或者等于min_sup_count的项以及对应的T(N)，删除{I1I4,I2I4,I2I5,I3I4,I4I5}。故得到频繁2-项集L2={I1I2:4,I1I3:5,I1I5:3,I2I3:5,I3I5:4}和频繁3-项集L3={I1I2I3:3,I1I2I3:3}。

（4）最终输出所有的频繁项集L=L1+L2+L3={I1,I2,I3,I4,I5,I1I2,I1I3,I2I3,I3I5,I1I2I3,I1I3I5}。

4 算法性能分析与实验

通过实验分析Apriori算法、Eclat算法、CBM_Apriori算法和CBM_Eclat算法的性能，它们都在相同的环境下进行比较。实验环境为：CPU为i7-4790、3.60GHz、内存4GB和Windows7系统，使用R语言编辑的程序。首先从R语言中自带的Groceries数据库中提取样本数据分别为1000、2000、3000、4000和5000；然后对Groceries数据库进行处理并使用K-medoids聚类算法，获得不同的样本布尔矩阵；最后使用CBM_Apriori算法和CBM_Eclat算法运行样本布尔矩阵，找到所有满足条件的频繁项集。当最小支持度相同时，则通过上述四种算法运行时间与样本数据之间的变化关系，如图2所示。当最小支持度不同时，则比较上述四种算法的性能，如图3所示。

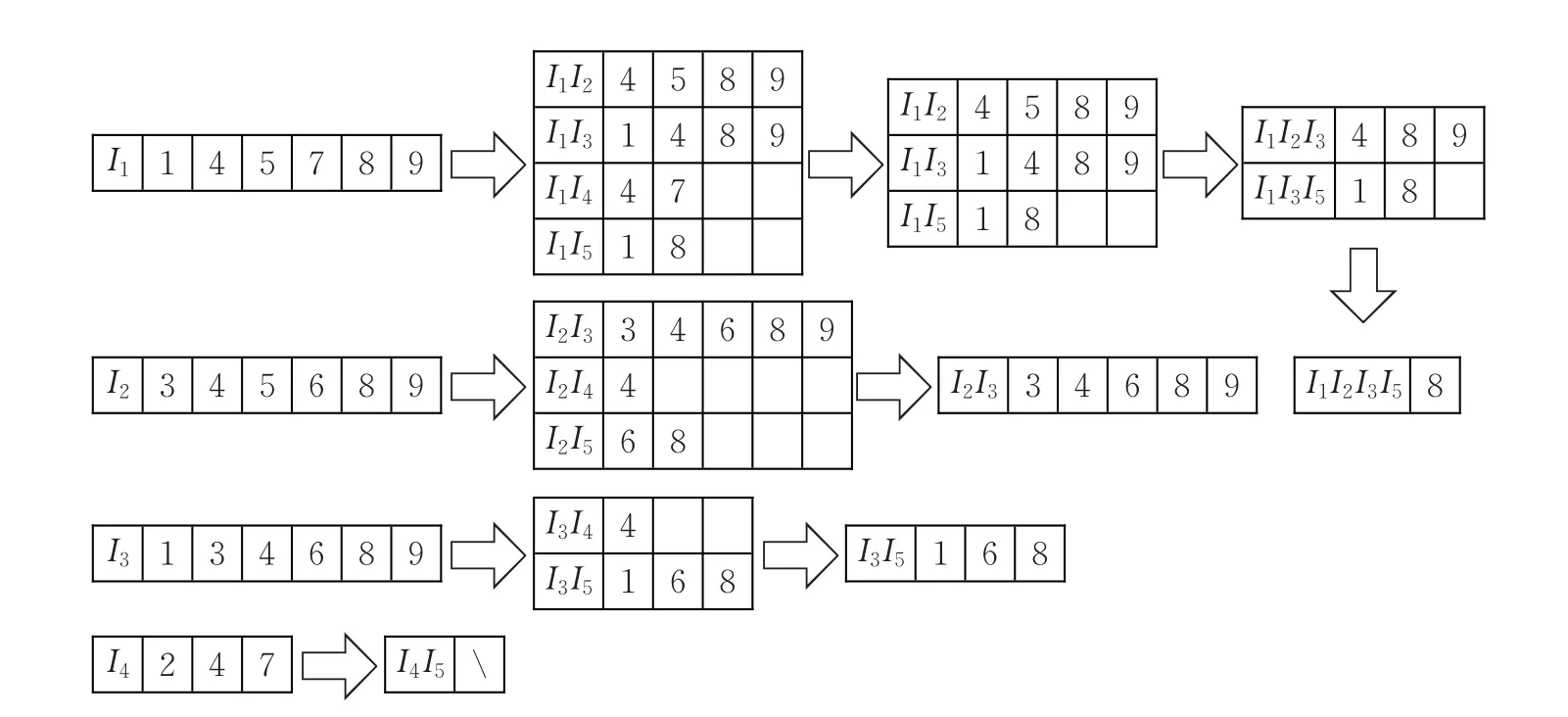
图1 候选项集和频繁项集

图2 四种算法运行时间与样本数据的变化关系

如图2所示，四条曲线变化趋势明显看出：经典Apriori算法随着样本数据的增加，其运行时间在快速的增加；Eclat算法、CBM_Apriori算法和CBM_Eclat算法随着样本数据的增加，其运行时间也在缓慢的增加；CBM_Apriori算法运行的速度也比经典的Eclat算法要快；本文改进的CBM_Eclat算法运行的速度比其他三个算法都要快，其中随着样本数的增加，时间变化更明显。

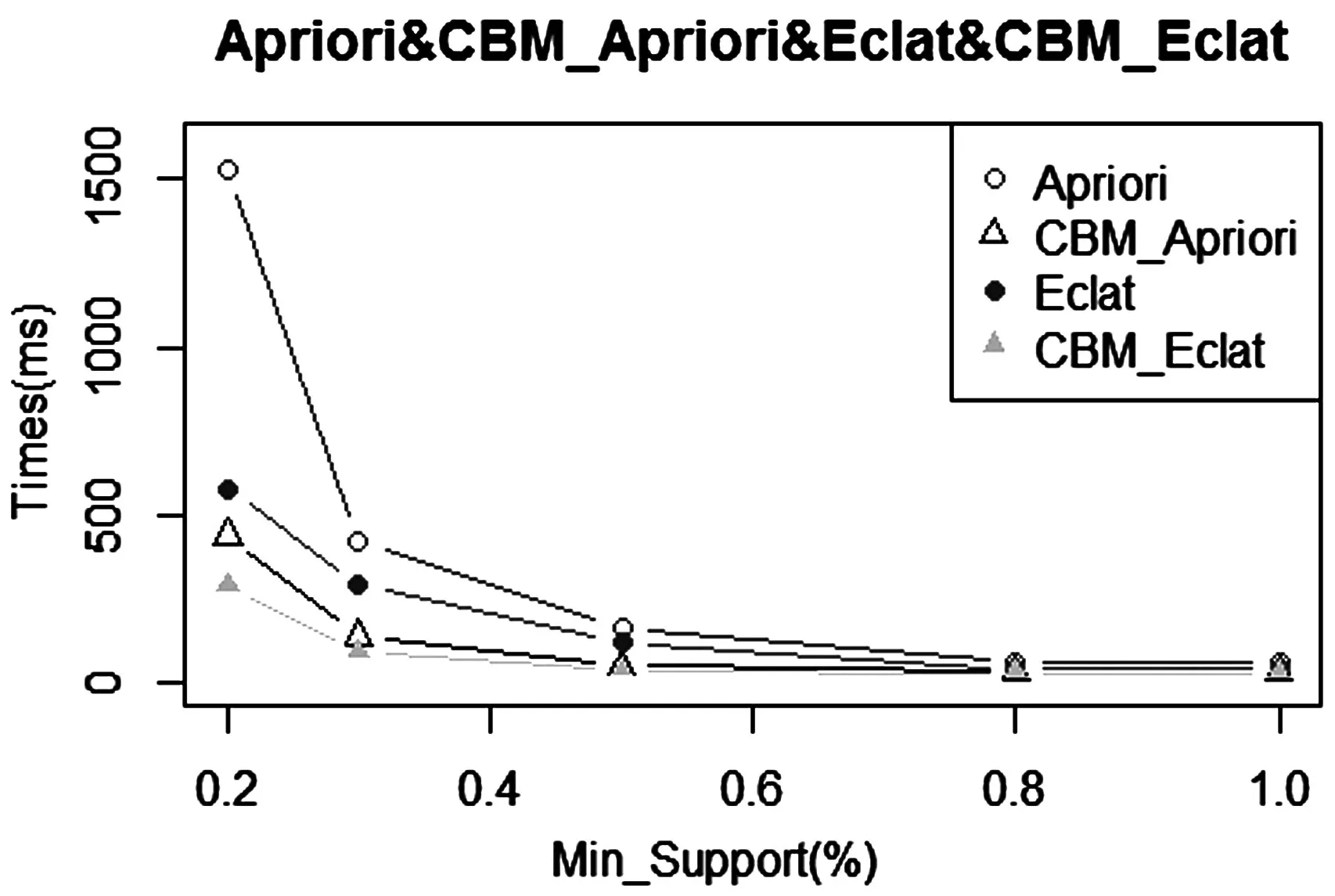
图3 最小支持度不同时四种算法的性能比较

如图3所示，当最小支持度越来越小时，经典Apriori算法要比其他三个算法运行的时间明显要多；而当最小支持度越来越大时，四个算法运行的时间也越来越少且基本上相等。

5 结论

随着数据挖掘技术的广泛应用，关联规则挖掘作为数据挖掘领域的主要研究课题之一，为了提高关联规则挖掘算法的运算效率，针对CBM_Apriori算法产生大量的候选项集和占用大量的存储空间等缺点进行改进。于是，提出了一种基于聚类布尔矩阵的Eclat算法—CBM_Eclat算法。该算法也只需要扫描事务数据库一次且采用逻辑“交”操作运算，减少候选项集的生成和存储空间，所以提高了该算法的执行效率。

［1］Agrawal R，Imielinaki T，Swami A.Mining association rules between sets of items in large databases［C］.InProc.1993ACM—SIGMOD Int.Conf.Management of Date，Washington，D.C.，1993：207-216.

［2］Jiawei Han，Jian Pei，Yiwen Yin.Mining frequent patterns without candidate generation［C］.In Proc.2000 ACM—SIGMOD Int.Conf.Management of Data，Dallas，Texas，USA，2000：1-12.

［3］Vu L，Alaghband G.A fast algorithm combining FP-tree and TID-list for frequent pattern mining［C］.In Proceedings of IEEE Conference on Information and Knowledge Engineering，2011：472-477.

［4］付沙，宋丹.基于矩阵的Apriori改进算法研究［J］.微电子学与计算机，2012，5（5）：156-161.

［5］Mohammed J Zaki.Scalable algorithms for association mining［J］.Knowledge and Data Engineering，2000，12（3）：372-390.

［6］Zaki M.J.Fast vertical mining using diffsets［R］.Technical Report 0-1，Rensselaer Polytechnic Institute，Troy，New York，2001.

［7］方炜炜，杨炳儒，宋威，等.基于布尔矩阵的关联规则算法研究［J］.计算机应用，2008，25（7）：1964-1967.

［8］李敏，李春平.频繁模式挖掘算法分析和比较［J］.计算机应用，2005，25（1）：166-171.

［9］宋长新，马克.改进的Eclat数据挖掘算法的研究［J］.微计算机信息，2008，24（8）：92-94.

［10］景永霞，王治和，杜跃.一种新的Apriori改进算法［J］，长春理工大学，2007，30（2）：67-69.

［11］谈恒贵，王文杰，李克双.频繁项集挖掘算法综述［J］，计算机仿真，2005，22（11）：1-4.

The Research of Apriori Algorithm Based on Cluster Boolean Matrix

TIAN Lei，CUI Guangcai，HE Xu，CHEN Jianxin
（School of Computer Science and Technology，Changchun University of Science and Technology，Changchun 130022）

For the inadequacy of Apriori algorithm of cluster Boolean matrix —CBM_Apriori algorithm，this paper presents a methods of Eclat algorithm based on cluster Boolean matrix —CBM_Eclat algorithm. To begin with，using K-medoids algorithm deal with Boolean matrix to obtain the weight and new Boolean matrix. Then，new Boolean matrix is transformed into the Tidset that use logical “and” operating，so the cluster Boolean matrix storage and candidate itemsets are reduced effectively. Thus，the efficiency of the algorithm is improved. Meanwhile，the application of example and result of algorithm performance both can prove the feasibility and effectiveness of the CBM_Eclat algorithm.

CBM_Apriori algorithm；CBM_Eclat algorithm；Boolean matrix；K-medoids algorithm；Tidset

TP311

A

1672-9870（2017）05-0109-06

2017-09-18

田磊（1989-），男，硕士研究生，E-mail：tl091138@163.com

崔广才（1964-），男，博士，教授，E-mail：gccui@cust.edu.cn