锥体导管架海洋平台冰激振动的DEM-FEM耦合分析及高性能算法

王帅霖,季顺迎*

锥体导管架海洋平台冰激振动的DEM-FEM耦合分析及高性能算法

王帅霖1,季顺迎1*

(1.大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连116023)

在寒区海域,冰荷载是影响海洋平台安全运行的主要环境荷载之一,由其引起的冰激振动给平台结构及其上部设备带来了严重危害。为分析不同冰况下平台的振动响应,本文建立了导管架海洋平台冰激振动的离散元(DEM)-有限元(FEM)耦合模型。采用具有黏接-破碎性能的等粒径球体离散单元对海冰的破碎特性进行模拟,通过由梁单元构建的海洋平台有限元模型获得结构的振动响应。在离散元与有限元的接触区域中实现了两个模型间计算参数的传递。为提高该耦合模型的计算效率和规模,发展了基于动力子结构方法的DEM-FEM耦合模型。为验证该耦合模型的有效性和可行性,将不同冰况下得到的冰荷载与ISO19906和JTS 144-1-2010标准进行了对比。结果表明,计算得到的冰荷载与标准相近,且冰厚与冰荷载呈二次非线性关系。同时,从冰速和冰厚两方面对比了渤海四桩腿JZ20-2 MUQ锥体导管架平台冰激振动加速度的数值结果和现场实测数据,发现冰速与振动加速度呈线性关系,冰厚与振动加速度呈二次非线性关系,并且振动加速度与冰速和冰厚平方的乘积呈线性关系。

冰荷载;冰激振动;锥体导管架平台;DEM-FEM耦合模型;动力子结构

1 引言

对于长期服役在寒区的海洋结构,海冰激励下的强烈振动是影响平台结构安全的重要因素之一。在渤海一般采用安装破冰锥改变海冰破碎形式减弱冰荷载的影响[1]。但通过现场监测,依然存在明显的冰激振动现象[2-3]。因此,需要对加锥平台的冰激振动开展分析。

对于冰激结构振动问题,由于室内试验和现场监测操作比较困难且花费较高。因此,数值模拟方法得到了快速发展[4-7]。季顺迎等[8]分别采用Duha mel积分方法以及基于海冰现场监检测统计的方法对渤海海洋平台的冰激振动响应进行分析;Kär nä和Tur unen[9]假设冰荷载为海冰与结构相对速度的函数,计算得到了平台的冰激振动响应;柳春光等[10]基于精细积分法的思想,给出了冰荷载的构造方法,并通过试验反演验证了结果的精度。但由于海冰大多以离散碎块的形式漂浮于海面,具有很强的非连续性,物理性质复杂[11],且当海冰相互碰撞或与海洋平台结构相互作用时,会进一步发生破碎。采用基于连续介质的理论描述海冰的力学行为有着其本身的局限性。

对于海冰的这种非连续分布特性及其破碎现象,可采用离散元方法(DEM)进行数值分析。近年来,海冰离散单元模型发展迅速,可以有效地模拟海冰的破碎现象并能较合理地反应不同结构冰荷载的特性[12]。其中,一种具有黏结-破碎特性的球体离散单元展现出很好的计算性能[13]。同时,海洋平台结构在海冰作用下的动力响应可采用有限元方法(FEM)进行计算。因此,对于海冰与海洋平台相互作用的数值模拟,可采用DEM-FEM耦合方法对其振动进行分析。

自20世纪90年代,DEM-FEM耦合模型不断发展和完善,是一种有效处理颗粒材料与工程结构、连续介质耦合作用的多尺度数值方法。目前,基于颗粒离散元的DEM-FEM耦合模型主要有3种,即模拟脆性材料断裂发展的组合有限-离散元模型、离散元-有限元区域间的耦合模型以及离散介质与连续体间的相互作用模型。连续体断裂的DEM-FEM耦合模型最早由Munjiza等建立[14],通过节理单元的断裂来模拟裂纹的扩展;第二种为离散元-有限元区域间的耦合,即对所要研究的局部用离散单元法进行细观尺度的描述,对其他区域用有限单元法进行宏观尺度的模拟[15];最后一种则主要用于模拟离散介质与连续体间的相互作用,实现两种介质边界条件间的传递[16],目前已应用于多个领域,如模拟轮胎与路面相互作用[17]、海底管线冲击问题[18]和流化床模拟[19]等。本文针对具有离散性的海冰与导管架海洋结构相互作用,提出了球体离散单元与梁单元在接触面上的耦合算法。

为提高DEM-FEM耦合模型在冰激海洋平台工程应用中的计算规模和效率,本文在有限元求解中,利用动力子结构法中的约束模态综合法[20]对平台自由度进行缩减,进而提高计算效率。当采用离散元-有限元耦合模型分析弹性结构在颗粒材料中的振动时,由于弹性结构大多复杂即自由度较多,直接分析的计算成本较大,如果结构的响应只由低阶模态控制,不必为少数低阶模态求解整个结构的高阶动力学方程,此时可以采用动态子结构法中的约束模态综合法降低结构自由度,提高模型的计算效率[21-22]。

为此,本文将针对海冰与海洋平台导管架结构相互作用的动力特性,分别采用DEM和FEM建立海冰与海洋平台导管架结构的数值模型,发展冰激海洋导管架平台结构振动的DEM-FEM耦合方法。为验证该DEM-FEM耦合模型的合理性,将计算结果与ISO19906和JTS 144-1-2010标准以及现场实测的结构振动加速度数据进行对比分析。

2 海冰与海洋平台相互作用的DEMFEM耦合模型

2.1 具有黏结-破碎特性的海冰离散元模型

为模拟平整冰的破碎特性,将具有黏接-破碎功能的等粒径球体单元规则排列构成平整冰离散元模型,如图1所示。每个黏接颗粒单元间具有一定的黏结强度以传递两个黏接单元间的作用力和力矩,如图2所示。黏接单元间的最大拉应力和剪应力可依据梁的拉伸、扭转和弯曲理论计算:

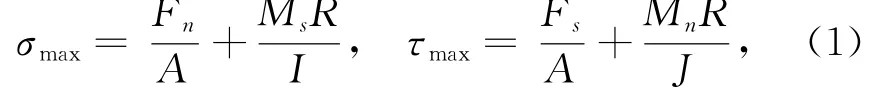
式中,A、J和I为黏结区域横截面的面积、极惯性矩和惯性矩;Fn和Fs为单元黏接面上的法向和切向作用力;Mn和Ms为黏结区域横截面的扭矩和力矩;R为黏接面的半径。

如果最大拉伸强度或者最大剪切强度超过了黏结单元相应的法向拉伸强度和剪切强度,单元间的黏结消失。这里黏结单元法向拉伸强度和剪切强度通过单轴压缩和三点弯曲数值试验确定[23],考虑了单元的尺度、单元间的摩擦系数以及宏观海冰强度对其的影响。黏接单元之间的失效模式采用考虑累积损伤的线性软化模型[13],其失效准则如图3所示,并可写作:

式中,knf为法向弹性损伤模量;un为法向相对位移;kn为法向接触刚度;ω为描述单元间出现损伤的程度,ω=0表示无损伤发生,0＜ω＜1时则出现损伤。ω可表示为:

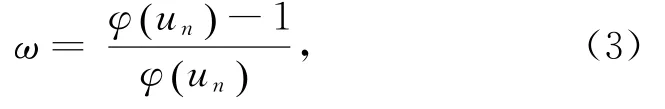
式中,φun()为法向相对位移的函数,可表示为:

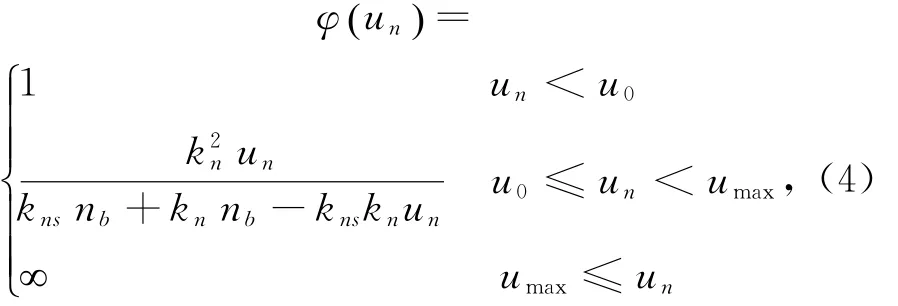
式中,kns为软化模量;nb为法向拉伸强度;u0为单元间的法向位移;umax为法向最大位移。

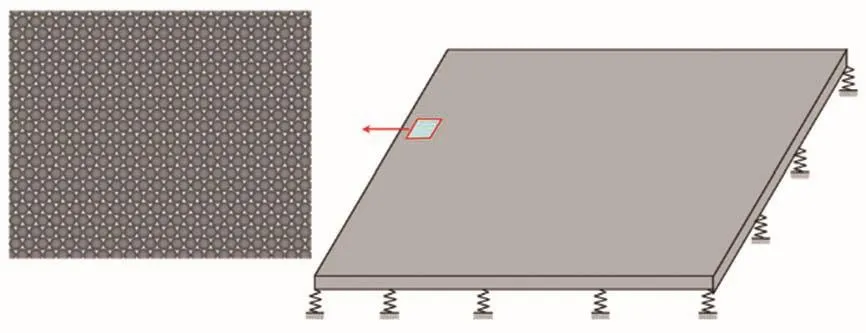
图1 等粒径球体的平整冰离散元模型Fig.1 The DEM model of level ice constructed by spheres with the same particle size

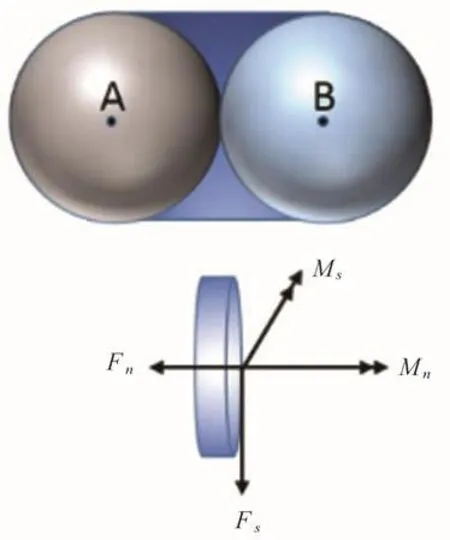
图2 球体离散单元平行黏结模型Fig.2 The parallel bonding model of spherical discrete elements

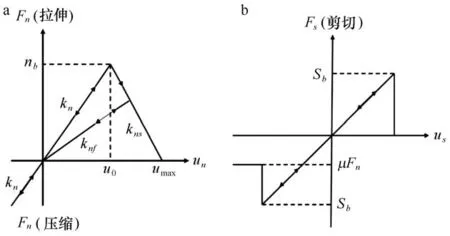
图3 黏结单元断裂的线性软化模型Fig.3 Linear softening model breaking process of bonded elementsa为法向力与法向位移的关系;b为切向力与切向位移的关系a.Relationship bet ween the nor mal force and nor mal displacement;b.relationship bet ween the shear force and shear displacement

2.2 锥体导管架海洋平台有限元模型

为研究渤海导管架海洋平台的冰激振动响应,针对该海域平台结构的特点,本文建立了渤海四桩腿锥体导管架平台(JZ20-2 MUQ)的有限元模型。该导管架平台主要由3部分组成,即上部模块、导管架和桩基。在有限元动力分析时,为简化计算,在保证主体结构几何形状以及结构振动频率和振型真实性的基础上,可对平台结构的有限元模型进行一定的简化。这里将上部结构简化为梁单元同时桩基用等效6倍的桩径代替,如图4所示。针对简化后的平台结构,采用经典的Ti moshenko梁单元进行求解。

图4 渤海JZ20-2 MUQ导管架海洋平台及其有限元模型Fig.4 The JZ20-2 MUQjacket platfor m and its FEM model in the Bohai Seaa为渤海JZ20-2 MUQ四桩锥体导管架平台;b为JZ20-2 MUQ四桩锥体导管架平台结构有限元模型a.The JZ20-2 MUQfour legs conical jacket platfor min the Bohai Sea;b.the FEM model of JZ20-2 MUQfour legs conical jacket platfor m

为提高动力分析的计算效率,采用动力子结构法中的约束模态综合法对结构的自由度进行缩减[20]。本文将整体平台结构划分为两个子结构,以JZ20-2 MUQ四桩腿锥体海洋平台结构为例,如图5所示。该平台结构各部分的动力学方程可表示为:

式中,u¨、u˙、u分别为节点的加速度、速度以及位移向量;M、C、K分别为结构的质量、阻尼和刚度矩阵,其中C用Rayleigh阻尼表示;F为外荷载;上标s代表各子结构的编号。

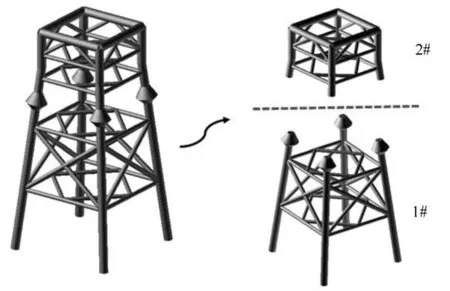
图5 JZ20-2 MUQ海洋平台结构有限元模型子结构的划分示意图Fig.5 Sketch of the FEM model of JZ20-2 MUQ platfor m divided into t wo sub-structures

2.3 海冰与导管架海洋平台的离散元-有限元耦合模型

采用DEM-FEM耦合模型分析平台冰激振动时,两模型间的参数传递尤为重要。这里,将海冰离散单元对导管架海洋平台结构的冰荷载作为力边界条件传递到有限元模型,由此计算海洋平台的动力响应,再进一步将更新后的平台位移作为离散元的位移边界条件。

本文海冰由球体离散单元构造,导管架海洋平台通过梁单元建立。关于球体离散单元与梁单元的接触力以及接触点的坐标可在局部坐标系下获得。同球体离散单元间的接触力计算相同,根据Hertz-Mindlin理论,球体离散单元与梁单元的接触力由法向和切向两部分组成,即:

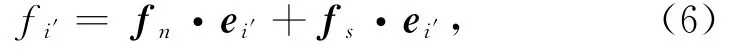
式中,fi'为局部坐标系下梁单元i'方向的接触力;ei'为局部坐标系下i'方向的单位向量;fn,fs分别通过DEM得到的法向和切向接触力。法向接触力由弹性和黏滞力组成,即:

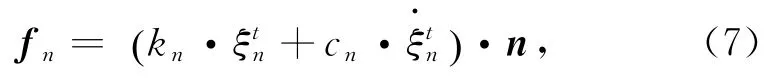
式中,n为球体离散单元与梁单元作用的法向单位向量;kn为球体离散单元与梁单元间的法向刚度系数;cn为球体离散单元与梁单元间的阻尼系数;ξtn为t时刻球体离散单元与梁单元的法向重叠量和法向相对速度,可表示为:

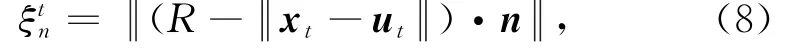
式中,R为球体的半径;xt为球体t时刻的位置向量;ut为梁单元t时刻的位置向量。

对于球体离散单元与梁单元切向力的计算,这里考虑Mohr-Coulomb摩擦准则,即:

式中,s为球体离散单元与梁单元作用的切向单位向量;f*s为当前的球体离散单元对梁单元的切向力,且不能超过最大静摩擦力;ks为球体离散单元与梁单元之间的切向刚度;μw为球体离散单元与梁单元间的摩擦系数;x˙st,u˙st分别为球体离散单元和梁单元在接触点处的切向速度;Δt为计算的时间间隔;sign x()为符号函数。

在海冰与海洋平台结构的作用过程中,球体离散单元与梁单元接触的位置是随机的,为此需确定海洋平台在冰荷载作用下的等效节点荷载。在局部坐标系下,假定梁单元的两端固定如图6所示,由静力平衡可求得局部坐标系下梁单元的等效节点力 Fe{ },即:

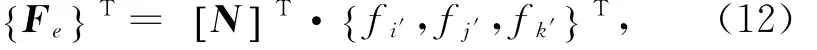
式中,N[]为等效节点力转换矩阵,由 NA,NB[ ]组成,可表示为:

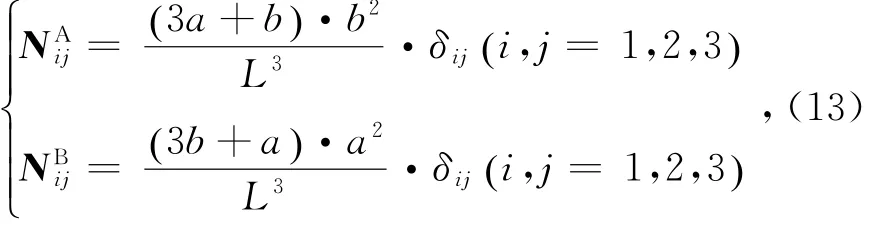
式中,L为梁单元的长度;a,b分别为接触点到两端节点的距离;δij为克罗内克符号。

在海洋平台结构的有限元计算中,结构振动响应采用逐步积分法中的New mar k方法计算。在保证离散元和有限元边界条件传递的基础上,时间步长的选取直接影响DEM-FEM耦合算法的实现。一般离散元的时间步长要远小于有限元的时间步长。为获得准确的计算结果,本文采取统一的时间步长,即离散元时间步长。在以后工作中,还需要进一步改进有限元和离散元模型在不同时间步长下的参数传递问题,从而在保障计算稳定性条件下提高计算效率。

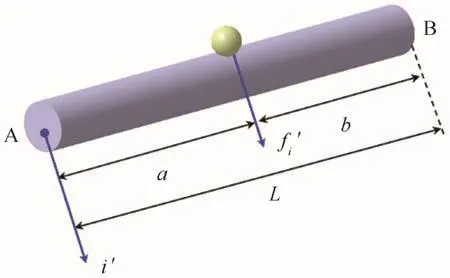
图6 梁单元等效力计算模型Fig.6 The equivalence force model of the beam element

3 JZ20-2 MUQ离散元-有限耦合模型冰激振动的验证及分析

下面通过与ISO19906、JTS144-1-2010标准以及渤海JZ20-2 MUQ锥体平台现场实测结构振动加速度数据对比,对提出的冰激结构振动的DEMFEM耦合模型进行验证。本文海冰离散元计算采用GPU并行算法对其进行加速[13],具体的海冰离散元计算参数如表1所列。在不同冰速和冰厚下模拟海冰与锥体海洋平台的相互作用,具体参数在表2中列出。

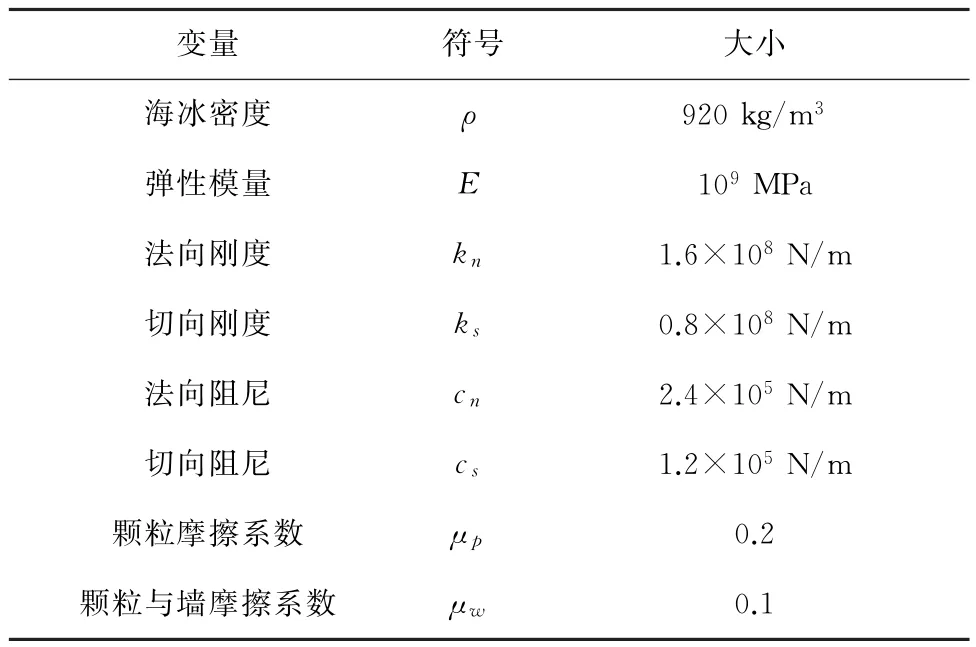
表1 海冰离散元模拟中的计算参数Tab.1 Computational parameters in the sea ice DEM

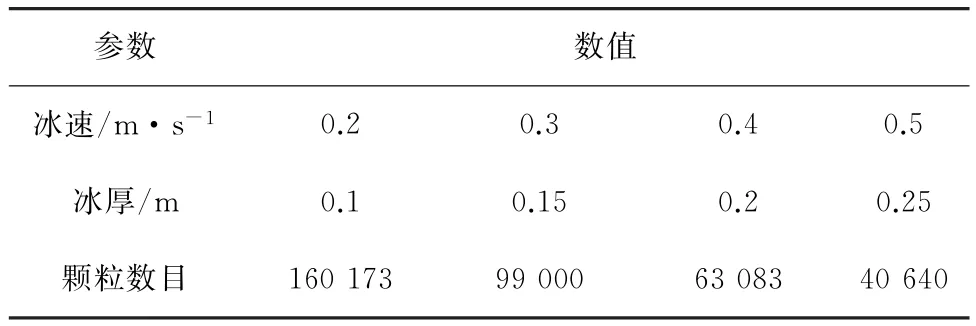
表2 离散元计算中的海冰条件Tab.2 Sea ice conditions in the DEMsi mulations

由此得到不同时刻(t=0.0 s,t=60.0 s,t=120.0 s,t=180.0 s)海冰与锥体导管架海洋平台相互作用的过程,发现海冰在桩腿切割下发生弯曲破坏并形成明显的水道,如图7所示。为进一步分析模拟得到的海冰在锥体前的破坏模式,分别给出了现场观测以及数值模拟海冰与锥体相互作用破碎的局部放大图,如图8所示。由图可以看出模拟的结果与现场观测的现象有很好的相似性,并且可以看到平整冰在锥体作用下的破碎情况,即冰排呈现出初次断裂、爬升、二次断裂和清除的过程,并由此引起交变动冰力。

3.1 JZ20-2 MUQ平台结构的冰荷载分析

多桩腿平台各桩上的冰荷载受海冰流向的影响,本文考虑水平冰向下平台结构所受的冰荷载,因此迎冰方向的两个桩腿为主要受力部分。由于结构的对称性以及海冰流向的特点,这里只需给出单个迎冰桩腿水平方向的冰力时程(vi=0.2 m/s,Hi=0.2 m),如图9所示,圆点表示冰力时程中的荷载峰值。从冰荷载时程中可以发现,桩腿上的冰荷载呈现多个峰值,并具有很强的随机性,这与海冰现场监测和室内模型试验结果相一致[24]。

为验证该DEM-FEM耦合模型的可行性与适用性,将模拟得到的冰荷载峰值分别与ISO19906标准[25]中的平整冰与锥体结构相互作用的冰荷载以及我国《港口工程荷载规范》JTS 144-1-2010标准[26]中正锥体上的水平冰力进行对比,如图10a所示。从图中发现通过标准得到的冰荷载以及数值计算获得的冰荷载峰值都与冰厚呈近似的二次非线性增加关系。但在冰荷载大小方面,JTS 144-1-2010标准要高于ISO19906标准所得到的冰荷载,而数值计算的结果比两个标准都要小。因为,本文采用的ISO19906标准计算锥体冰荷载的公式是基于弹性梁理论的冰断裂力部分,而JTS 144-1-2010标准则采用正锥体上水平冰荷载的计算公式,存在较多的经验系数,使得结果相对保守。另外,离散元计算参数的选取直接影响冰荷载的计算结果,如单元黏结强度、单元尺寸、层数等计算参数的确定还需要进一步的分析研究。为进一步分析冰速和冰厚对冰荷载的影响,给出了不同冰速下冰厚与冰荷载均值的关系,如图10b所示。从图中可以看出冰荷载均值随冰厚呈非线性增加,而对冰速变化并不敏感。

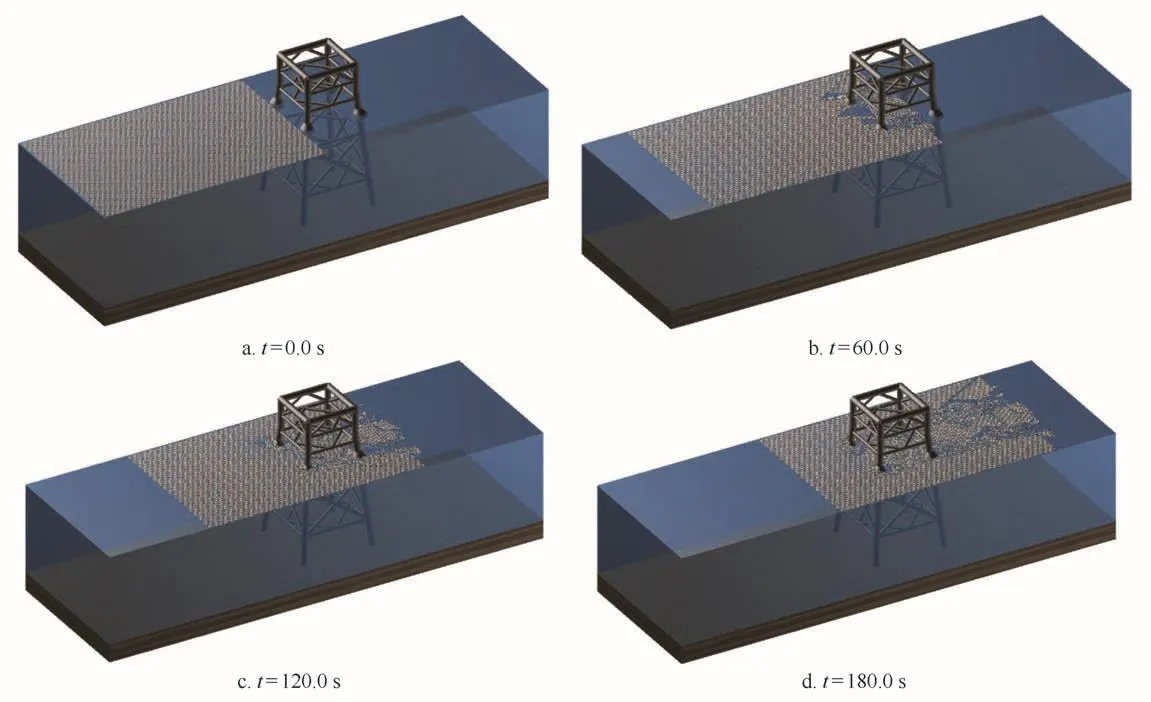
图7 DEM-FEM模拟的海冰与JZ20-2 MUQ平台相互作用过程(H i=0.2 m,v i=0.2 m/s)Fig.7 Interactions bet ween sea ice and JZ20-2 MUQ platfor m si mulated with DEM-FEM(H i=0.2 m,v i=0.2 m/s)

图8 海冰与锥体相互作用时的断裂现象Fig.8 Fracture phenomenon of sea ice cover during interaction bet ween sea ice and conical platfor ma为海冰在锥体前破坏的现场监测情况;b为DEM-FEM模拟中海冰在锥体前的破坏模式a.Failure of seaiceinteracted with the conical observed in field;b.failure of seaiceinteracted with the conical si mulated with DEM-FEM method

3.2 JZ20-2 MUQ平台结构的冰激振动分析

由于海冰与结构的相互作用属于随机过程,为避免随机性对结果造成影响,数值模拟的时间要足够充分,本文的模拟时间分别为220 s、160 s、120 s和90 s。首先,给出相同冰况下(vi=0.2 m/s,Hi=0.2 m)现场实测的振动数据和数值模拟得到的平台冰激振动加速度时程,如图11所示。从图中可观察到实测和数值结果都在0.04～-0.04 m/s2范围内变化,具有较好的相似性。下面将对数值结果和实测数据进行较详细的对比分析。

下面分别将不同冰速和冰厚下得到的振动加速度峰值与渤海实测数据进行对比分析,如图12a和12b所示。图中圆点代表现场实测5 min内结构振动的最大值,通过DEM-FEM耦合方法得到的振动加速度峰值用三角形表示,两条虚线分别代表实测数据和数值结果的趋势。由于现场实测的冰况复杂涉及冰厚、冰速、冰向、温度等多种因素,因此在将模拟结果与实测数据对比时,选取数值模拟范围内的实测数据点更具普遍意义。

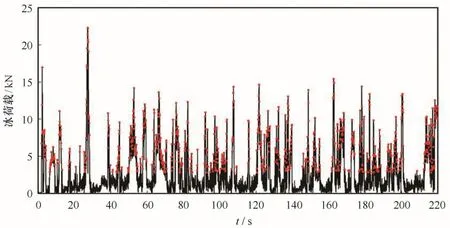
图9 离散元计算的桩腿冰荷载时程(v i=0.2 m/s,H i=0.2 m)Fig.9 Ice forces on the platfor m si mulated with DEM(v i=0.2 m/s,H i=0.2 m)

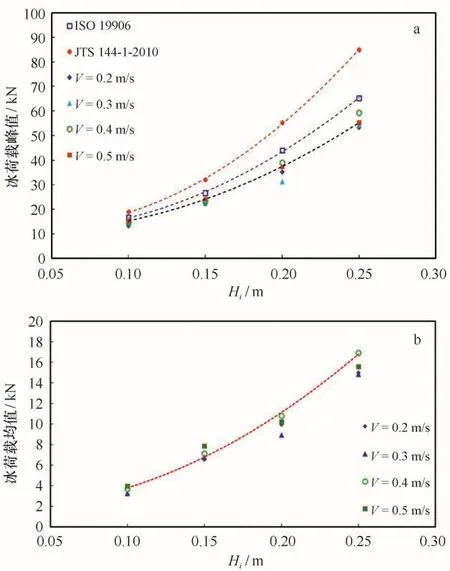
图10 模拟得到的冰荷载与ISO19906、JTS 144-1-2010标准对比Fig.10 Ice forces comparing bet ween numerical and ISO19906,JTS 144-1-2010 standarda为DEM-FEM耦合模型的冰荷载峰值与ISO19906、JTS 144-1-2010标准对比;b为冰厚与DEM-FEM耦合模型的冰荷载均值的关系a.Ice forces comparing bet ween the coupled DEM-FEM model and ISO19906,JTS 144-1-2010 standards;b.relationship bet ween ice thickness and averaged ice forces obtained by the coupled DEMFEM model

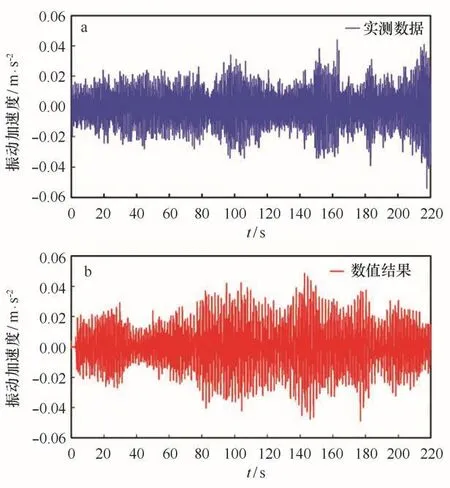
图11 v i=0.2 m/s,H i=0.2 m时平台的冰激振动加速度时程Fig.11 The ice-induced vibration acceleration of the platfor m with v i=0.2 m/s,H i=0.2 ma为平台结构冰激振动加速度现场实测数据;b为DEMFEM耦合模型的冰激振动加速度a.The ice-induced vibration acceleration of the platfor m observed datain field;b.theice-induced vibration accelerations of the platfor m obtained by the coupled DEM-FEM model

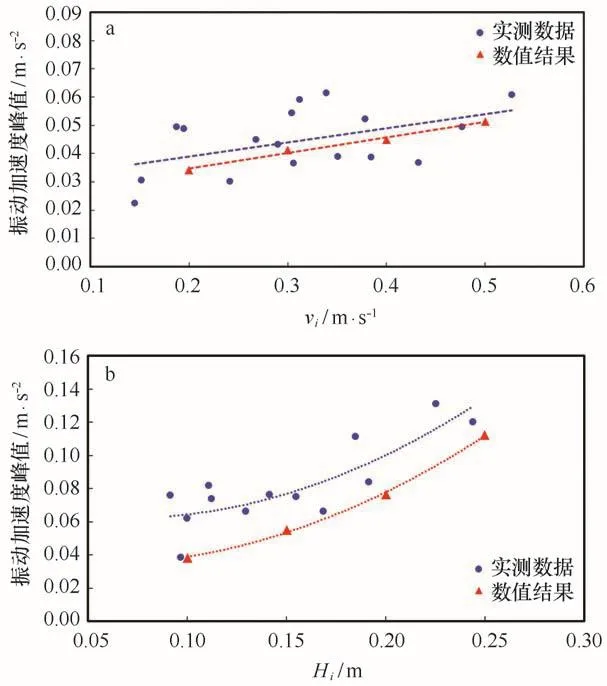
图12 不同冰况下平台结构冰激振动加速度数值结果与实测数据的对比Fig.12 Ice-induced vibration accelerations of the platfor m compared bet ween the si mulation and field data with different ice conditionsa为不同冰速下平台结构振动加速度计算值与实测值对比(H i=0.2 m);b为不同冰厚下平台结构振动加速度计算值与实测值对比(v i=0.5 m/s)a.Comparison bet ween si mulated results and field data under different ice velocities(H i=0.2 m);b.comparison bet ween si mulated results and field data under different ice thicknesses(v i=0.5 m/s)

由图12a可以发现数值结果与实测结果的趋势基本保持一致。即冰速与振动加速度呈线性增加关系,冰厚与振动加速度呈二次非线性增加关系。但由于本文数值计算中只引入了冰速、冰厚两个冰况参数,并没有考虑海冰强度、海冰流向等因素对结构振动的影响,导致数值结果与实测数据存在一定的差异性,这也将在接下来的工作中进一步考虑。

为说明冰速、冰厚对结构振动加速度的影响,根据动量定理将海冰离散单元单位时间步内输入结构的能量写作:

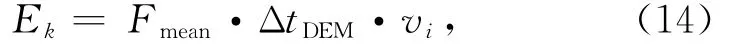
式中,Ek为输入结构的能量;Fmean是通过DEMFEM耦合模型计算得到的冰荷载均值;ΔtDEM为离散元的计算时间步;vi为海冰的流速。

根据式(14)可得到不同冰况下结构输入海冰能量的趋势图,如图13所示。图13a为冰厚为0.2 m时不同冰速下输入结构的能量,圆点代表输入结构的能量值。图13b为冰速为0.5 m/s时,不同冰厚传递给结构的能量,其中三角形表示输入结构的能量值。从图13a和图13b可以发现冰速、冰厚与能量的关系与图12所示的关系是一致的,即冰速与能量呈线性增加关系,冰厚与能量则呈二次非线性关系。

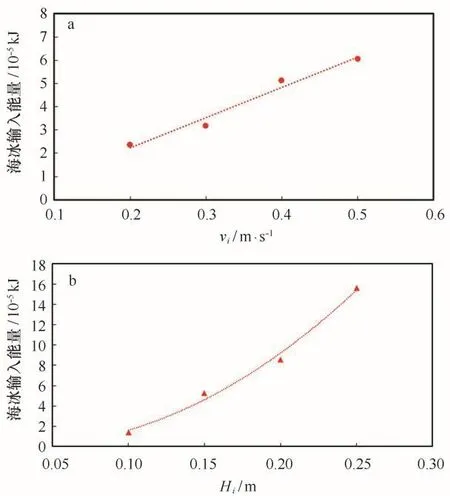
图13 不同冰况下锥体平台结构输入的海冰能量Fig.13 Energy of the platfor m under different ice condition induced by sea icea为不同冰速下锥体平台结构输入的海冰能量(H i=0.2 m);b为不同冰厚下锥体平台结构输入的海冰能量(v i=0.5 m/s)a.Energy of the conical platfor m under different ice velocities induced by sea ice(H i=0.2 m);b.energy of the conical platfor m under different ice thicknesses induced by sea ice(v i=0.5 m/s)

根据渤海JZ20-2 MUQ平台现场冰激振动加速度测量数据的统计,发现冰激振动加速度与冰速和冰厚平方的乘积呈线性关系[8]:

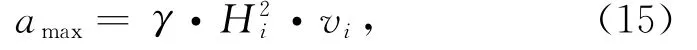
式中,amax为振动加速度的峰值;Hi为海冰的厚度;vi代表海冰的流度;γ为相关的线性系数。

根据式(15)所示的统计规律,将模拟的16种工况按照式(15)参数进行重新组合,如图14所示。图中横坐标代表冰速与冰厚平方的乘积,纵坐标为冰激振动加速度的峰值,数据点分别代表现场检测数据以及数值模拟得到的结果。从中可以看到实测数据和数值模拟的结果较为接近且符合式(15)的关系。这说明本文提出的DEM-FEM耦合模型可以揭示渤海锥体导管架海洋平台冰激振动的一般性规律。另外,从输入结构能量的角度,可以发现冰速和冰厚的平方与输入结构的海冰能量都呈线性关系。且假设冰速和冰厚为相互独立变量,因此冰速与冰厚平方的乘积也应与输入结构的海冰能量呈线性关系,从结构能量上解释了冰激振动加速度与冰速和冰厚的关系。

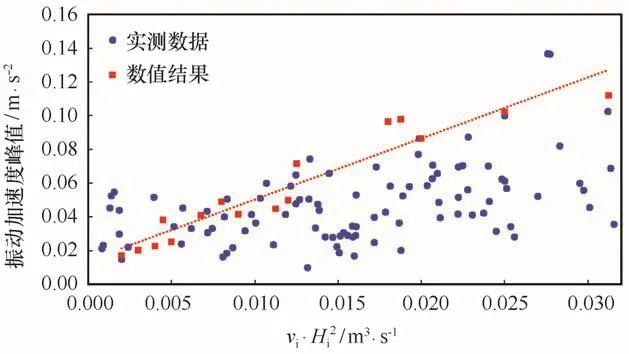
图14 冰速、冰厚与JZ20-2 MUQ平台结构冰激振动加速度的关系Fig.14 The relation bet ween the ice velocity,ice thickness and ice-induced vibration of the JZ20-2 MUQ platfor m

4 结论

本文主要提出了模拟导管架海洋平台冰激振动的DEM-FEM耦合模型,同时考虑了海冰的破碎效应以及结构的振动响应。采用具有黏接-破碎特性的离散单元模拟海冰的破碎过程,由梁单元组成的多桩腿导管架有限元模型计算结构的动力响应,并发展了两个模型边界间计算参数的传递算法,建立了海冰离散元和导管架海洋平台结构有限元的冰激振动耦合模型。同时,采用GPU并行算法和动力子结构的方法提高了离散元和有限元部分的计算效率,得到了不同冰速、冰厚下结构所受到的冰荷载大小以及结构的振动响应。在冰荷载计算方面,通过耦合方法得到的冰荷载与ISO19906和JTS 144-1-2010标准相接近,并且冰厚与冰荷载呈现二次非线性关系,冰速对冰荷载的影响并不明显。对于平台结构的冰激振动加速度,计算结果与渤海JZ20-2 MUQ锥体平台现场实测的振动数据有着较好的一致性,且冰速与振动加速度呈线性关系,冰厚与振动加速度呈二次非线性关系,并得到了与实测振动统计关系式一致的规律,即振动加速度与冰速和冰厚平方的乘积呈线性关系。

因此,可以通过本文提出的DEM-FEM耦合模型对寒区导管架海洋结构的冰激振动进行分析,为寒区海洋结构的抗冰设计以及安全预警提供一种新的数值分析方法。但实际工程中,海冰流向、海冰强度以及波浪等因素对结构的振动都会产生影响。为更加合理的分析冰激海洋平台的振动问题,将会进一步考虑构建复杂冰况,并对结果进行谱分析,从频率方面揭示冰激振动的规律。

[1] 徐田甜,张晓,崔航.我国海上导管架平台抗冰锥体的设计实践[J].船舶工程,2010,32(2):73-77.Xu Tiantian,Zhang Xiao,Cui Hang.Design practices of anti-ice structure on offshorejacket platfor m of our country[J].Ship Engineering,2010,32(2):73-77.

[2] 黄焱,马玉贤,罗金平,等.渤海海域单柱三桩式海上风电结构冰激振动分析[J].海洋工程,2016,34(5):1-10.Huang Yan,Ma Yuxian,Luo Jinping,et al.Analyses on ice induced vibrations of a tripod piled offshore wind turbine str ucture in Bohai sea[J].The Ocean Engineering,2016,34(5):1-10.

[3] Yue Q,Zhang L,Zhang W,et al.Mitigating ice-induced jacket platfor m vibrations utilizing a TMDsystem[J].Cold Regions Science&Technology,2009,56(2/3):84-89.

[4] 王翎羽,徐继祖.冰与结构动力相互作用的理论分析模型[J].海洋学报,1993,15(3):140-146.Wang Lingyu,Xu Jizu.Theoretical analysis model of interaction bet ween ice and structure[J].Haiyang Xuebao,1993,15(3):140-146.

[5] 陈新权,谭家华.导管架平台在冰荷载作用下的动力响应分析研究[J].中国海洋平台,2005,20(4):25-28.Chen Xinquan,Tan Jiahua.Dynamic response analysis of jacket platfor m under ice load[J].China Offshore Platfor m,2005,20(4):25-28.

[6] 欧进萍,段忠东,王刚.海冰作用下平台结构自激振动的参数分析与响应的数值计算[J].工程力学,2001,18(5):8-17.Ou Jinping,Duan Zhongdong,Wang Gang.Parametric analysis and response si mulation of self-excited ice-induced vibration of offshore platfor m structures[J].Engineering Mechanics,2001,18(5):8-17.

[7] 李春花,王永学,李志军,等.半圆型防波堤前海冰堆积模拟[J].海洋学报,2006,28(4):172-177.Li Chunhua,Wang Yongxue,Li Zhijun,et al.The si mulation sea-ice cli mb-up and pile-up process on semicircle breakwater[J].Haiyang Xuebao,2006,28(4):172-177.

[8] 季顺迎,王安良,车啸飞,等.锥体导管架海洋平台冰激结构振动响应分析[J].海洋工程,2011,29(2):32-39.Ji Shunying,Wang Anliang,Che Xiaofei,et al.Analysis of ice-induced structure vibration of offshore jacket platfor m with ice breaking cone[J].The Ocean Engineering,2011,29(2):32-39.

[9] KärnäT,Turunen R.Dynamic response of narrow structures to ice cr ushing[J].Cold Regions Science&Technology,1989,17(2):173-187.

[10] 柳春光,齐念,冯晓波.精细积分在冰荷载识别中应用[J].海洋工程,2010,28(2):65-70.Liu Chunguang,Qi Nian,Feng Xiaobo.Applications of t he preciseintegration toiceload identification[J].The Ocean Engineering,2010,28(2):65-70.

[11] 王安良,许宁,毕祥军,等.卤水体积和应力速率影响下海冰强度的统一表征[J].海洋学报,2016,38(9):126-133.Wang Anliang,Xu Ning,Bi Xiangjun,et al.Unified representation of seaice strengths under influences of brine volume and stress rate[J].Haiyang Xuebao,2016,38(9):126-133.

[12] Polojärvi A,Tuhkuri J,Pustogvar A.DEMsi mulations of direct shear box experiments of ice r ubble:Force chains and peak loads[J].Cold Regions Science&Technology,2015,116:12-23.

[13] 狄少丞,季顺迎.海冰与自升式海洋平台相互作用GPU离散元模拟[J].力学学报,2014,46(4):561-571.Di Shaocheng,Ji Shunying.GPU-based discrete element modelling of interaction bet ween seaice and jack-up platfor mstructure[J].Chinese Journal of Theoretical and Applied Mechanics,2014,46(4):561-571.

[14] Munjiza A,Lei Z,Divic V,et al.Fracture and frag mentation of thin shells using t he combined finite-discrete element met hod[J].International Journal for Numerical Methods in Engineering,2013,95(6):478-498.

[15] 张锐,唐志平.三维离散元与壳体有限元耦合的时空多尺度方法[J].工程力学,2010,27(4):44-50.Zhang Rui,Tang Zhiping.A multiscale method of ti me and space by coupling three-di mensional DEMand cylindrical shell FEM[J].Engineering Mechanics,2010,27(4):44-50.

[16] Chung Y C,Lin C K,Chou P H,et al.Mechanical behaviour of a granular solid and its contacting defor mable structure under uni-axial compression-Part I:Joint DEM-FEM modelling and experi mental validation[J].Chemical Engineering Science,2015,144:404-420.

[17] 赵春来,臧孟炎.基于FEM/DEM的轮胎-沙地相互作用的仿真[J].华南理工大学学报:自然科学版,2015,43(8):75-81.Zhao Chunlai,Zang Mengyan.Si mulation of tire-sand interactions based on FEM/DEM[J].Journal of Sout h China University of Technology:Natural Science Edition,2015,43(8):75-81.

[18] Rah man M A,Taniyama H.Analysis of a buried pipeline subjected to fault displacement:A DEMand FEM study[J].Soil Dynamics&Earthquake Engineering,2015,71:49-62.

[19] 赵永志,江茂强,徐平,等.埋管流化床内传热行为的微观尺度模拟研究[J].浙江大学学报:工学版,2010,44(6):1178-1184.Zhao Yongzhi,Jiang Maoqiang,Xu Ping et al.Micro-scale si mulation of heat transfer behavior in fluidized bed with i mmersed tube[J].Journal of Zhejiang University:Engineering Science,2010,44(6):1178-1184.

[20] Hurty W C.Vibrations of structural systems by co mponent mode synthesis[J].Journal of the Engineering Mechanics Divion,ASCE,1960,86:51-59.

[21] 向树红,邱吉宝,王大钧.模态分析与动态子结构方法新进展[J].力学进展,2004,34(3):289-303.Xiang Shuhong,Qiu Jibao,Wang Dajun.The resent progresses on modal analysis and dynamic sub-structure methods[J].Advancesin Mechanics,2004,34(3):289-303.

[22] 冯青松,张翊翔,万鹏,等.动态子结构法在地铁列车引起地基振动分析中的应用[J].铁道科学与工程学报,2014(6):52-57.Feng Qingsong,Zhang Yixiang,Wan Peng,et al.Application of dynamic sub-structuring methodin the analysis of foundation vibration caused by metro train[J].Journal of Rail way Science and Engineering,2014(6):52-57.

[23] Ji S Y,Di S C,Long X.DEMsi mulation of uniaxial compressive and flexural strength of seaice:parametric study[J].Jour nal of Engineering Mechanics,2016,143(1):C4016010.

[24] 史庆增,黄焱,宋安,等.锥体冰力的实验研究[J].海洋工程,2004,22(1):88-92.Shi Qingzeng,Huang Yan,Song An,et al.Experi mental study of ice force on conical structure[J].The Ocean Engineering,2004,22(1):88-92.

[25] Blanchet D,Spring D,Mc Kenna R F,et al.ISO 19906:An International Standard for Arctic Offshore Structure[S].Houston:Offshore Technology Conference,2011.

[26] 中华人民共和国交通运输部.JTS 144-1-2010港口工程荷载规范[S].北京:人民交通出版社,2010.Ministry of Transport of the People's Republic of China.Load code for harbor engineering JTS 144-1-2010[S].Beijing:China Communications Press,2010.

Iceinduced vibration of conical platfor mbased on coupled DEM-FEM model with high efficiency algorithm

Wang Shuailin1,Ji Shunying1

(1.State Key Laborator y of Structure Anal ysis of Industrial Equip ment,Dalian University of Technology,Dalian 116023,China)

In cold regions,the vibrations of offshore platfor ms induced by sea ice can be har mful for not only the routine production but also the serviceability and safety of platfor ms.In this study,a coupled discrete element method(DEM)and finite element method(FEM)is developed to analyze the seaice-conical jacket platfor minteraction and iceinduced vibrations of the platfor m.The DEM with bonding-breaking effect bet ween bonded spherical elements is adopted to si mulate the breakage of ice cover and the FEMis applied to model the ice-induced vibrations of jacket platfor m with the beam element.The trans missions of the mechanical variables at the interface bet ween DEMand FEMare achieved in this paper.In additionally,to i mprove the computational efficiency and scale of the coupled model,the coupled model based on the dynamic sub-structure method is adopted here.In order to verify the effectiveness of the proposed method,ISO19906 and JTS 144-1-2010 standards under variousice velocities and thicknesses are compared with the si mulated ice load.The si mulated ice load is in good confor mance with the standard.Meanwhile,the si mulation accelerations obtained by the proposed method are compared with observation data of the four-pile conical platfor m(JZ20-2 MUQ),which show the high consistency.In addition,the results alsoindicate that the vibration acceleration of the platfor mis linearly related toice velocity,quadratic nonlinearity to ice thickness,and linearly related to the product of the ice velocity and ice thickness squared.

ice force;ice-induced vibration;conical offshore platfor m;coupled DEM-FEM;dynamic sub-structure method

O343.3;P751

A

0253-4193(2017)12-0098-11

王帅霖,季顺迎.锥体导管架海洋平台冰激振动的DEM-FEM耦合分析及高性能算法[J].海洋学报,2017,39(12):98-108,

10.3969/j.issn.0253-4193.2017.12.010

Wang Shuailin,Ji Shunying.Iceinduced vibration of conical platfor mbased on coupled DEM-FEM model with high efficiency algorithm[J].Haiyang Xuebao,2017,39(12):98-108,doi:10.3969/j.issn.0253-4193.2017.12.010

2016-12-30;

2017-05-31。

国家重点研发计划(2016 YCF1401505,2016 YFC1402705,2016 YFC1402706);国家自然科学基金项目(41576179,51639004)。

王帅霖(1990—),男,辽宁省鞍山市人,主要从事离散元-有限元耦合方法研究。E-mail:dlut_wsl@sina.co m

*通信作者:季顺迎(1972—),男,河北省武邑县人,博士,教授,主要从事工程海冰数值模型研究。E-mail:jisy@dlut.edu.cn