波浪水槽中振动格栅湍流特征的实验研究
马洪余,戴德君,乔方利,蒋暑民
波浪水槽中振动格栅湍流特征的实验研究
马洪余1,2,3,戴德君2,3*,乔方利2,3,蒋暑民2,3
(1.中国海洋大学 海洋与大气学院,山东 青岛266100;2.海洋环境科学和数值模拟国家海洋局重点实验室,山东 青岛266061;3.国家海洋局第一海洋研究所,山东 青岛266061)
在波浪水槽中采用格栅振动的方式产生湍流,研究振动格栅产生湍流的特征。本文开展了4类实验,调节测量点到格栅平均位置的距离、格栅振动频率、振动冲程,采用ADV测量水体中单点的脉动速度。实验结果显示,湍流强度在一定范围内随离格栅距离的增大而逐渐减小,随着振动频率的增大而呈幂指数增大,随着振动冲程的增大而呈幂指数增大。同时还比较了两个不同格栅产生湍流的不同。结果显示,在波浪水槽中,振动格栅产生湍流的强度还与格栅的长度尺寸有关,这与在水箱中振动格栅产生湍流的特征不同。
波浪水槽;振动格栅;湍流
1 引言
湍流是海洋中的重要物理过程,它对大洋环流,海气之间的动量、热量和物质交换以及生物过程等都有重要影响。在真实的海洋中湍流总是由流剪切、波浪破碎、对流等过程产生,湍流过程比较复杂,并与其他物理过程共同存在,对湍流很难有比较清楚的认识。为了对湍流特征能够有比较清楚的了解,已开展大量的室内实验,在水箱中用振动格栅、射流泵产生均匀各向同性湍流,研究湍流特征,进而研究湍流与泥沙运动的相互作用[1]、湍流对气泡分布规律的影响、污染物扩散等问题。
自从1939年Rouse[1]第一次采用振动格栅产生湍流研究泥沙悬浮以来,Rouse和Dodu[2]也采用振动格栅产生湍流的方式研究两层流体的湍流混合,继而围绕着振动格栅产生湍流开展了大量的研究工作,并且更多生成湍流的方式也被相继提出。在实验室水箱中产生湍流的方法主要有两种:一种是单一平面能量源产生湍流[3-7],例如,振动格栅和随机射流阵,可产生二维均匀、各向同性湍流,但由于垂直方向湍流的衰减,无法产生三维的、均匀且各向同性湍流[8];另一种对称能量源产生湍流[9-17],例如,对称射流阵组成的对称系统,对称振动格栅,围绕对称中心区域在水箱的8个角落安装喷嘴等,在对称区域(中心区域或者平面)产生均匀、各向同性湍流,且平均流较小,其缺点是质量最好的湍流位于中心区域,此湍流不能用来研究边界处的湍流特征。在实验室水箱中产生湍流的优点是,可以重复产生稳定的、同一强度的、均匀的、近似各向同性湍流。
在水箱中,由单一平面能量源产生湍流,在与平面能量源平行的二维平面上湍流是均匀且各向同性的,而在垂直于平面的方向上wrms/urms>1,其中wrms和urms分别是垂直和水平流速分量的均方根,不均匀也不具有各向同性特征,且在垂直于平面的方向上湍流是逐渐衰减的。已有研究指出[4,6,18],振动格栅产生湍流wrms/urms∈[1.1,1.4]。Variano和Cowen[7]研究发现由射流阵产生湍流,wrms/urms=1.27。而由对称系统可以在中心区域产生三维均匀、各向同性湍流[19-22]。
振动格栅产生湍流,湍流强度u'与格栅冲程S、振动频率f、到格栅平均位置的距离z和网孔大小M有关系。其关系式为u'=C1S3/2M1/2f z-1,其中C1有不同的取值,C1≈0.25[4],C1≈0.22[6]。水体自由表面对湍流有影响,影响区域从z=-15 c m开始直至水体自由表面[23],在评价湍流强度时,上述关系式在此区域不适应。
平均流的存在,对水体混合和输运有显著影响,然而在水箱中由振动格栅产生湍流时,平均流的产生是不可避免的[7],且以下几个因素更有助于平均流的增强:格栅条占整个格栅面积大于40%[24],网格边界的不对称性[25-26],大的振动冲程[27],振动频率大于7 Hz[18,21],因此,要获得平均流较小的湍流,需要调节振动格栅的各个参数。为比较不同方式产生湍流时平均流的强度,定义=/urms,衡量平均流的大小,其中表示速度分量u的时间平均。Variano等[19]研究结果指出,振动格栅产生湍流的典型情况0.25,最好的情况0.1,最差的情况>1。Variano和Cowen[7]的研究由射流阵产生湍流,给出0.07。而对称系统比单一振动格栅产生的平均流要小,Hwang和Eaton[16]的实验结果为=0.02。
已有研究,在水槽中产生湍流的工作很少,王得祥等[28]在水槽中利用振动格栅产生湍流,但其振动格栅安装在水槽一端,通过振动装置,使得格栅往复运动产生湍流,研究了湍流强度与格栅振动频率的关系,以及湍流强度与到格栅平面距离的关系,对湍流的均匀性和平均流等特征没有过多的研究。
综上所述,湍流的产生和特征研究多数是在水箱中开展,而在水槽中产生湍流并研究其特征的工作较少。波-湍相互作用已有大量的实验室实验研究工作,然而,在已有的室内实验工作中,波浪由造波系统生成,而湍流却没有很好的办法产生。Thais和Magnaudet[29]是用吹风的方式产生湍流,这样却很难认识背景湍流场的强度。因此,采用合适的方法在水槽中产生背景湍流,研究湍流的特征,是很有必要的。本文将振动格栅架设于波浪水槽上方,通过格栅的上下振动产生湍流,研究不同格栅振动频率、振动幅度以及格栅长度下湍流的特征,为后续波-湍相互作用研究奠定基础。
2 实验设置
国家海洋局第一海洋研究所风-浪-流多功能实验水槽于2012年建成并投入使用,其长45 m,宽1 m,高1.8 m,最大水深1.2 m,本实验在此水槽中开展。在水槽的中间位置选择一段为实验段,将振动格栅的变频电机架设于独立于水槽的支架之上,格栅通过连接杆与电机的偏心轮连接,格栅则浸入到水体中,电机转动带动偏心轮旋转,既而带动格栅上下振动,如图1所示。这种架装方式有效地把格栅与水槽分开,可以防止电机振动通过边壁传递到水槽的水体中,进而消除对格栅振动产生湍流的影响。格栅沿水槽方向的边缘距离水槽边壁为4 c m,而垂直于水槽方向的格栅边缘是开阔的。实验过程中水槽水深为1.2 m,格栅平均位置水深为47 c m。
格栅为长方形,由不锈钢板打孔构造而成,孔的边长为5 c m×5 c m,孔与孔的中心距离为6 c m,格栅条的宽度为1 c m,不锈钢板的厚度为3 mm,边长为91 c m×295 c m,格栅条的面积与格栅总面积之比约为31.6%,即小于40%,满足产生稳定均匀湍流的条件[24]。格栅振动时,在格栅的背面会产生射流和尾迹流,这些射流和尾迹流向外延展,相互合并,但不偏离它们的轴线,逐渐失去平均动量,在离格栅一定的距离之后形成均匀的湍流。当此数值大于40%时,格栅振动产生的射流会偏移并且与其他射流合并形成更强的射流,从而形成平均流,影响产生湍流的质量。振动格栅产生湍流的强度与振动频率和格栅冲程有关,本实验中通过调节变频电机调节振动格栅的频率,设定振动频率为1 Hz、2 Hz和3 Hz,小于7 Hz[18],通过调节偏心轮来调节格栅振动的幅度,设定振动冲程为3 c m、5 c m和7 c m。格栅上下运动时,在距格栅平均位置大于2~3倍格栅孔径的距离处[30],形成近似各向同性湍流。
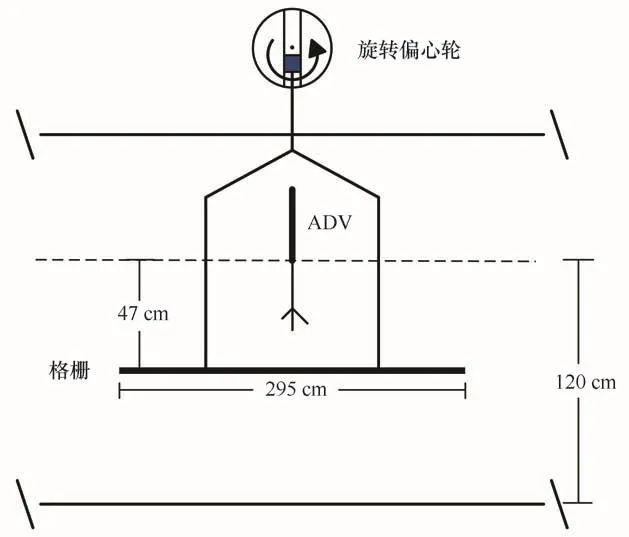
图1 振动格栅和实验设置示意图Fig.1 The diagram of the oscillating grid and laboratory setup
利用声学多普勒流速仪ADV(Nortek小威龙一代)测量水体的脉动速度,获得单点的三维流速(u,v,w),其中u表示沿水槽方向的水平流速,v表示垂直于u方向的水平流速,而w表示垂向流速,其最高采样频率为200 Hz,在本实验中采用128 Hz进行采样,测量精度为(测量值的±0.5%)±1 mm/s。测量点为一圆柱体,直径为6 mm,高度为3~15 mm。测量点位于格栅平面的中心位置,通过调节ADV探头的深度获得湍流的垂直剖面速度。
ADV在获得单点的速度场时,同时也获得反向散射的声学信号强度和连续pings的相关性[31],这两个参数用来诊断ADV的数据质量。信号强度依赖于散射体的密度[32],散射体较少时,反向散射信号强度较弱,速度信号不可靠。在采样体积内,流体速度有扰动或者有剪切[33],或者在相邻pings时散射体离开采样体积时[34],相关性较低;在水体中含有大量气泡[35]和采样体积接近海底时(一个采样体体积的宽度)[36-37]同样导致相关性较低,低相关性导致不精确的速度测量[31]。因而在处理ADV数据时需要对测量数据进行质量控制,主要有3种方法:方法1,用ADV的速度值去除野点(比标准差大一定倍数,加速度超过阈值);方法2,相空间质量控制方法[38-39];方法3,信号强度和相关系数方法。在处理本实验由ADV获得的数据时,需要先对数据做质量控制,在本文中采用方法1对数据进行数据处理,然后再对数据做相应的分析。
3 实验结果
利用ADV获得单点三维流速场(u,v,w),以水平速度分量u(x,t)为例,将其分解为时间平均速度u(x)与脉动速度u'(x,t),并以速度的均方根大小评价湍流的强度[7],
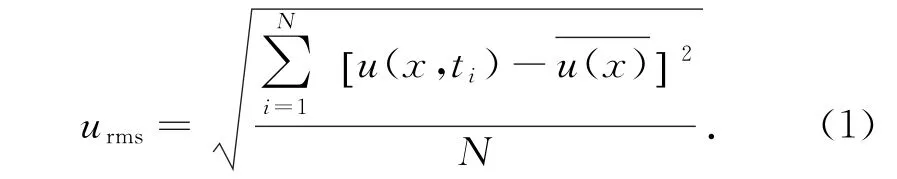
同时研究湍流强度随深度的变化关系,以及与格栅振动频率、格栅冲程的关系,湍流的均匀性、各向同性特征及平均流大小等。
本文共开展了4类实验:实验1,湍流强度随深度变化实验;实验2,湍流强度随振动频率变化实验;实验3,湍流强度随冲程变化实验;实验4,两个格栅的比较实验,如表1所示。

表1 实验及参数设置Tab.1 Experimental design
3.1 实验1湍流强度随深度变化实验
格栅上下振动产生湍流,格栅冲程为5 c m,振动频率为3 Hz,连续向上移动ADV,每次移动4 c m,共计获得5个不同深度位置,在分析湍流强度随深度变化的规律之前,先分析湍流的均匀性和平均流等特征。
格栅在水平面以下平均水深为47 c m的位置上下振动产生湍流,随着到格栅距离的增加,湍流强度逐渐减弱。从湍流速度3分量的功率谱可以清晰的看出湍流的均匀性和湍流强度。图2给出了湍流速度3个分量的功率谱,从谱上可以清晰的看到,水平方向两分量u和v的功率谱线基本重合,即在水平方向上湍流强度一致,湍流均匀;而垂直分量w的功率谱线显著低于水平方向u和v的功率谱线,即垂向的湍流强度比水平方向的湍流强度弱,这与在水箱中格栅振动产生湍流的特征wrms/vrms>1是不一致的。而在w分量的功率谱上还有一个显著的特征,即在3 Hz处有一个锋值,此表示水体有一3 Hz的垂向运动,此即是格栅的上下振动,此特征与Öl mez和Milgram[40]的实验结果相同。
格栅振动产生湍流,不可避免的产生平均流,用10 min速度场的平均作为平均值,用U/urms衡量平均流的大小,得出U/urms≈0.18,与Variano等[19]的研究结果接近。
分析湍流强度随深度变化的规律,由图3a可知,湍流强度随着到格栅距离的增大,先减小,这符合格栅振动产生湍流的规律,然后再增大,这不符合格栅振动产生湍流的特征。分析其原因是,在波浪水槽中,格栅振动产生湍流的区域沿水槽方向是敞开的,从而导致湍流在水平方向上传递,且传递到格栅振动区域以外的水体中,在垂直方向传递减小,进而导致在垂直方向远离格栅的位置处湍流的特征变差,反而增多了一些大尺度的平均流动,再用简单的时间平均方法去掉平均值得到湍流时,已不能准确的分离出湍流脉动速度,导致湍流强度增大。
在计算湍流强度时,需要减去一个平均值,图3a所示结果是减去10 min速度场的平均值,从结果可以看出,10 min速度的平均值,不能很好地代表流体的平均运动。因为在10 min的速度中,包括了低频的流体运动,用简单的时间平均,不能很好地去掉这种低频的平均运动,从而导致计算湍流强度的增大。本文试图对上述相同的速度分量u采用滑动平均的方法,将这种低频的平均运动滤掉之后再计算湍流强度,滑动窗口的大小取为128×10+1(1 281),约10 s,结果如图3b所示。
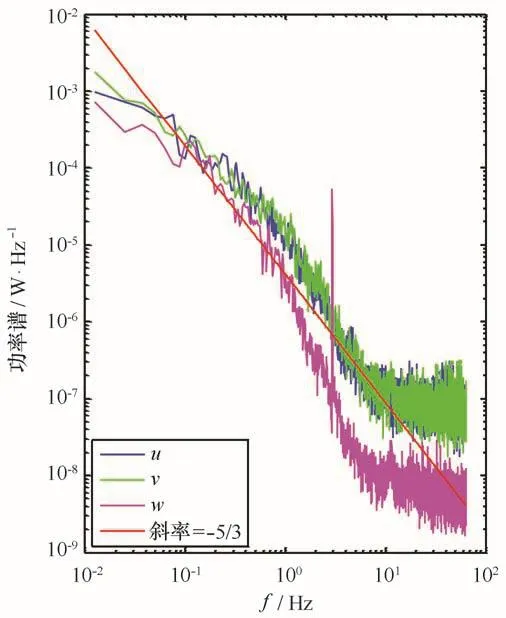
图2 湍流速度3分量的功率谱Fig.2 The power spectra of turbulent velocity three components

图3 实验1中湍流强度随深度变化规律,其中u的平均值由时间平均(a)和滑动平均(b)获得Fig.3 The turbulence strength changes with depth,where the mean value of u is computed through ti me average(a)and s mooth average(b)respectively in experi ment 1
由图3b可知,在采用滑动平均方法去掉平均值以后,湍流强度随着到格栅距离的增大而减小,即从深度32.2 c m,到28.2 c m,再到24.2 c m,湍流强度逐渐减小,且符合幂指数为负数的幂函数衰减规律,其幂函数拟合曲线为:urms=3.75(47-D)-0.53,其中D表示测量点深度,与图3a所示结果不同。在图3a中,湍流从深度32.2 c m到28.2 c m是减小的,但是到24.2 c m湍流强度没有变化,可见低频运动对湍流强度的评价有影响,且随着到格栅距离的增大,这种低频的流动会更显著,所以在20.2 c m和16.2 c m的深度上,即便采用滑动平均的方法,湍动强度依然没有衰减,而是增大。
3.2 实验2湍流强度随振动频率变化实验
在不同深度,随着格栅振动频率增加湍流强度有相似的变化规律,因此可以任意选取一深度处ADV测量值,分析湍流强度随频率的变化特征,这里选择水深为28.2 c m,格栅冲程为5 c m,振动频率分别设置为1 Hz、2 Hz、3 Hz,以水平速度分量u为例,分析湍流强度随频率的变化规律,结果如图4所示。从图4可以看出,湍流强度随格栅振动频率的增大而增大,但与振动频率并不是线性增大关系,而是以幂次小于1的幂函数增大,其幂函数拟合曲线为:urms=0.48f0.71。格栅振动频率增大,格栅向水体提供更多的能量,自然产生的湍流强度相应增强,但随频率增大的关系却不同。此实验是在两端敞开的水槽中产生湍流,其湍流强度随频率的变化特征是以幂次小于1的幂函数增大,而在水箱中湍流强度随频率线性增大[4],分析其原因是,在水槽中,沿水槽方向格栅两端是敞开的,湍流向格栅影响之外的区域扩散,而在水箱中则不会,从而导致与水箱中的湍流特征略有不同。

图4 实验2湍流强度随格栅振动频率的变化规律Fig.4 The variation of turbulence strength with frequency in experiment 2
3.3 实验3湍流强度随格栅冲程变化实验
ADV测量点到格栅平均位置的距离为18.5 c m,即水深28.5 c m,格栅振动频率设为2 Hz,格栅振动冲程为3 c m、5 c m和7 c m,分析湍流强度urms随格栅振动冲程S的变化规律,结果如图5所示。
格栅冲程是格栅上下振动时其最高位置与最低位置之间的距离,在一个周期内完成两个冲程过程。从图5可以看出,随着格栅冲程的增大,湍流逐渐增强,且不是线性增强,而是以幂次大于1的幂函数增强,其幂函数拟合曲线为:urms=(0.125S)2.6+0.63,这与在水箱中格栅产生湍流的特征相似。可见改变格栅冲程,可以有效地改变格栅振动产生湍流的强度。

图5 实验3湍流强度随格栅振动冲程的变化规律Fig.5 The variation of turbulence strength with strokes in experiment 3
3.4 实验4两个格栅的比较实验
构造两个格栅,一个是前文所述长方形格栅;另一个是正方形格栅。正方形格栅由相互垂直的格栅条构成,格栅条的截面尺寸为1 c m×1.5 c m,格栅边长为91 c m×91 c m,厚度为1.5 c m,格栅孔为边长5 c m×5 c m的正方形,相邻格栅孔中心的距离为6 c m,格栅条面积与总格栅面积之比为32.1%,小于40%。两个格栅的相同点是,格栅的孔径都为5 c m×5 c m的正方形,格栅条的宽度为1 c m,即相邻两个孔中心的距离为6 c m。不同点是,长方形格栅的一个边较长是295 c m,此格栅振动时,会扰动更多水体;长方形格栅由不锈钢板打孔而成,由于只是一块薄板,其强度不够,容易弯曲、变形,故在不锈钢板的背面加有支柱,而正方形格栅是由厚度为1.5 c m的格栅条构成;格栅条与整个格栅的面积比,两个格栅略有不同。
测量点到两个格栅的平均位置都为18.5 c m,两个格栅的冲程为5 c m,调节格栅振动的频率1 Hz、2 Hz、3 Hz,比较两个格栅产生湍流的强度。
在水箱中,由格栅振动产生湍流,其湍流强度与到格栅平均位置的距离、格栅振动频率、格栅振动冲程、孔心距这4个量有关,如果这4个量相同,湍流强度至多相差一个常数倍[4,6]。在此比较实验中,这4个量都相同,然而产生的湍流强度却不同,如图6所示,在振动频率为3 Hz时,正方形格栅产生湍流的强度大于长方形的2倍,并且它们随振动频率的变化趋势也不同,长方形格栅湍流强度随格栅振动频率增加的比较缓慢,而正方形格栅湍流强度随振动频率增加的比较迅速。
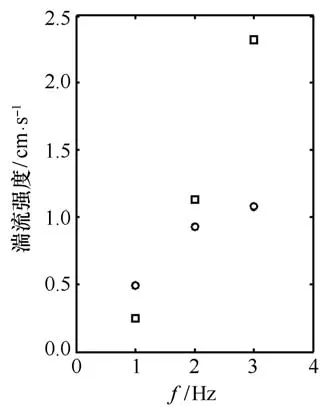
图6 实验4两不同格栅(长方形格栅(○)和正方形格栅(□))湍流强度随格栅振动频率的变化规律Fig.6 The variation of the turbulence strength with frequency of t wo grids:the rectangle grid(○)and the square grid(□)in experi ment 4
图7 显示了两个格栅振动频率为3 Hz时,分别获得的10 min水平速度分量u的时间序列。从图7可以看出,正方形格栅振动时,u变化比较剧烈,主要表现在低频的大幅度振动,主要原因是正方形格栅在沿水槽方向只有91 c m,且在此方向上两端是敞开的,水体比较容易进出格栅振动影响的区域,从而产生低频的大振幅流动,湍流强度较大;而长方形格栅的u,低频振动的振幅较小,在±4 c m/s之间,显然湍流强度较小,其原因是,长方形格栅沿水槽方向有295 c m,格栅影响的区域较长,我们的测量点位于格栅的中心位置,不易产生低频的大振幅流动。分别选取3 s的水平速度分量u,仔细比较其高频振动,发现正方形格栅u的振幅为0.16 c m/s比长方形格栅的0.28 c m/s要小。

图7 两不同格栅(长方形格栅(a)和正方形格栅(b))冲程为5 c m、频率为3 Hz时,速度分量u的时间序列Fig.7 The series of velocity co mponent u changes with ti me when t wo different grids(a indicates the rectangle grid and b indicates the square grid)vibrate with 5 c m strokes and 3 Hz frequency
而在振动频率为1 Hz时,正方形格栅的湍流强度要比长方形格栅湍流强度小,原因是,在振动频率为1 Hz时,两个格栅的低频振动幅度都很小,而长方形格栅的高频振动的幅度要比正方形的大,所以长方形格栅的湍流强度要大。
在波浪水槽中,由于两端是敞开的,格栅振动产生的湍流强度,不仅与格栅冲程、频率、孔心距有关,还与格栅的长度有关,这与在水箱中由格栅振动产生的湍流不同。
4 结论
在水箱中利用振动格栅产生湍流,此方面已有大量的研究工作。本文是在波浪水槽中,利用振动格栅产生湍流,其与在水箱中的最大不同在于,波浪水槽沿水槽方向是敞开的,进而使得振动格栅产生湍流具有自己的特征。
本文主要开展了4类实验,由实验结果可知,湍流强度随着到格栅平均位置距离的增加逐渐衰减,但在更远的距离时,湍流强度又增加,这主要是由于低频大幅度流动引起的;格栅产生湍流强度随着振动频率的增加而增加,增加不是以线性关系增加,而是以幂指数小于1的幂函数增加;随格栅冲程的增大,产生湍流强度以幂指数大于1的幂函数增加;构造了两个格栅,一个是长方形格栅,一个是正方形格栅,在格栅冲程、孔心距以及测量点到格栅平均位置的距离都相同的条件下,调节格栅振动的频率为1 Hz、2 Hz和3 Hz,实验结果发现,长方形格栅湍流强度随格栅振动频率增加的比较缓慢,而正方形格栅湍流强度随振动频率增加的比较迅速,并且在振动频率为1 Hz时,长方形格栅产生的湍流强度大,而在振动频率为3 Hz时,正方形格栅产生的湍流强度大,分析其原因为,格栅的长度不一样,进而在振动时产生的低频大幅度流动不一致,从而导致在计算湍流强度时,得到的湍流强度有差别。
总之,在波浪水槽中由振动格栅可产生水平方向近乎均匀、垂直方向湍流强度逐渐衰减、平均流较小的湍流,且可以通过调节格栅振动频率、振动冲程和改变格栅长度调节湍流强度大小,为开展后续的波-湍相互作用实验,湍流对气体交换影响实验,提供可控的背景湍流。
[1] Rouse H.Experi ments on the mechanics of sedi ment suspension[C]//Proceedings of the 5t h international congress of applied mechanics.Cambridge,MA,1939:550-554.
[2] Rouse H,Dodu J.Turbulent diffusion across a density discontinuity[J].La Houille Blanche,1955,10(4):522-532.
[3] Tho mpson S M,Turner J S.Mixing across an interface due to turbulence generated by an oscillating grid[J].Jour nal of Fluid Mechanics,1975,67(2):349-368.
[4] Hopfinger EJ,Toly J A.Spatially decaying turbulence and its relation to mixing across density interfaces[J].Journal of Fluid Mechanics,1976,78(1):155-175.
[5] Brumley B H,Jirka G H.Near-surface turbulencein a grid-stirred tank[J].Journal of Fluid Mechanics,1987,183:235-263.
[6] De Silva I P D,Fernando H J S.Oscillating grids as a source of nearly isotropic turbulence[J].Physics of Fluids,1994,6(7):2455-2464.
[7] Variano E A,Cowen E A.A random-jet-stirred turbulence tank[J].Journal of Fluid Mechanics,2008,604:1-32.
[8] Maxey M R.The velocity skewness measured in grid tur bulence[J].Physics of Fluids,1987,30(4):935-938.
[9] Douady S,Couder Y,Brachet M E.Direct observation of theinter mittency of intense vorticity filamentsin turbulence[J].Physical Review Letters,1991,67(8):983-986.
[10] Viller maux E,Sixou B,Gagne Y.Intense vortical structures in grid-generated tur bulence[J].Physics of Fluids,1995,7(8):2008-2013.
[11] Srdic A,Fer nando HJ S,Montenegro L.Generation of nearly isotropic turbulence using t wo oscillating grids[J].Experi mentsin Fluids,1996,20(5):395-397.
[12] Shy S S,Tang C Y,Fann S Y.A nearly isotropic turbulence generated by a pair of vibrating grids[J].Experi mental Ther mal and Fluid Science,1997,14(3):251-262.
[13] Voth G A,Satyanarayan K,Bodenschatz E.Lagrangian acceleration measurements at large Reynolds numbers[J].Physics of Fluids,1998,10(9):2268-2280.
[14] Liu S,Katz J,Meneveau C.Evolution and modelling of subgrid scales during rapid straining of turbulence[J].Journal of Fluid Mechanics,1999,387:281-320.
[15] Birouk M,Sarh B,Gökalp I.An attempt to realize experi mental isotropic turbulence at low Reynolds number[J].Flow,Turbulence and Combustion,2003,70(1/4):325-348.
[16] Hwang W,Eaton J K.Creating homogeneous and isotropic turbulence without a mean flow[J].Experi mentsin Fluids,2004,36(3):444-454.[17] Webster D R,Brathwaite A,Yen J.A novel laboratory apparatus for si mulatingisotropic oceanic turbulence at low Reynolds number[J].Li mnology and Oceanography:Methods,2004,2(1):1-12.
[18] Mcdougall T J.Measurements of turbulencein a zero-mean-shear mixed layer[J].Journal of Fluid Mechanics,1979,94(3):409-431.
[19] Variano E A,Bodenschatz E,Cowen E A.A randomsynthetic jet array driven turbulence tank[J].Experimentsin Fluids,2004,37(4):613-615.[20] Krawczynski J F,Renou B,Danaila L.The structure of the velocity field in a confined flow driven by an array of opposed jets[J].Physics of Fluids,2010,22(4):045104.
[21] Goepfert C,MariéJ L,Chareyron D,et al.Characterization of a system generating a homogeneousisotropic turbulence field by free synt hetic jets[J].Experi ments in Fluids,2010,48(5):809-822.
[22] Bellani G,Variano E A.Homogeneity and isotropy in a laboratory tur bulent flow[J].Experi ments in Fluids,2014,55(1):1-12.
[23] Hunt J C R,Graham J M R.Free-streamturbulence near plane boundaries[J].Journal of Fluid Mechanics,1978,84(2):209-235.
[24] Corrsin S.Turbulence:experi ment met hods[J].Handbuch der Physik,Stromungs Mechanik,1963,8:524-587.
[25] Xuequan E,Hopfinger E J.On mixing across an interface in stably stratified fluid[J].Journal of Fluid Mechanics,1986,166:227-244.
[26] Cheng N S,Law A WK.Measurements of turbulence generated by oscillating grid[J].Journal of Hydraulic Engineering,2001,127(3):201-208.
[27] Yi Y K,Lyn D A.Scaling and inhomogeneities in oscillating-grid flows[C]//Building Partnerships.ASCE,2000:1-10.
[28] 王得祥,王得军,李艳.水槽中振动格栅紊流特性实验研究[J].华北水利水电学院学报,2007,28(2):19-21.Wang Dexiang,Wang Dejun,Li Yan.Experi mental study on characteristics of oscillating-grid turbulencein flu me[J].Journal of Nort h China Institute of Water Consercancy and Hydrielectric Power,2007,28(2):19-21.
[29] Thais L,Magnaudet J.Turbulent structure beneath surface gravity waves sheared by the wind[J].Journal of Fluid Mechanics,1996,328:313-344.
[30] Atkinson J F,Damiani L,Harleman D R F.A comparison of velocity measurements using alaser anemometer and a hotfil mprobe,with application to grid-stirring entrain ment experi ments[J].Physics of Fluids(1958-1988),1987,30(10):3290-3292.
[31] Zedel L,Hay A E,Cabrera R,et al.Perfor mance of a single-beam pulse-to-pulse coherent Doppler profiler[J].IEEE Journal of Oceanic Engineering,1996,21(3):290-297.
[32] Lohr mann A,Cabrera R,Kraus N C.Acoustic-Doppler veloci meter(ADV)for laboratory use[C]//Fundamentals and advancementsin hydraulic measurements and experi mentation.ASCE,1994:351-365.
[33] Cabrera R,Deines K,Brumley B,et al.Develop ment of a practical coherent acoustic Doppler current profiler[C]//OCEANS'87.IEEE,1987:93-97.
[34] Lher mitte R,Lemmin U.Open-channel flow and turbulence measurement by high-resolution Doppler sonar[J].Journal of At mospheric and Oceanic Technology,1994,11(5):1295-1308.
[35] Mori N,Suzuki T,Kakuno S.Noise of acoustic Doppler velocimeter datain bubbly flows[J].Journal of Engineering Mechanics,2007,133:122-125.
[36] Martin V,Fisher T S R,Millar R G,et al.ADV data analysis for turbulent flows:Low correlation problem[C]//Proceedings of Hydraulic Measurements and Experi mental Methods Conference.2002.
[37] Elgar S,Raubenhei mer B,Guza R T.Quality control of acoustic Doppler veloci meter datain the surfzone[J].Measurement Science and Technology,2005,16(10):1889-1893.
[38] Goring D G,Nikora V I.Despiking acoustic Doppler veloci meter data[J].Journal of Hydraulic Engineering,2002,128(1):117-126.
[39] Wahl T L.Discussion of“Despiking acoustic Doppler veloci meter data”by Derek G.Goring and Vladi mir I.Nikora[J].Journal of Hydraulic Engineering,2002,128(1):117-126.
[40] Öl mez H S,Milgram J H.An experi mental study of attenuation of short water waves by turbulence[J].Journal of Fluid Mechanics,1992,239:133-156.
An experi mental study on characteristics of turbulence generated by oscillating grids in a wave tank
Ma Hongyu1,2,3,Dai Dejun2,3,Qiao Fangli2,3,Jiang Shu min2,3
(1.College of Oceanic and At mospheric Sciences,Ocean University of China,Qingdao 266100,China;2.Key Laborotr y of Marine Science and Nu merical Modeling,State Oceanic Ad ministr ation,Qingdao 266061,China;3.The First Institute of Oceanography,State Oceanic Ad ministration,Qingdao 266061,China)
In this paper,we study the characteristics of turbulence generated by oscillating grids in a wave tank.Four experi ments are carried out.High-frequency velocity fluctuations with different depths of measurement points,vibration frequency,vibration stroke were recorded by an acoustic Doppler veloci meter(ADV).The experi ments results show that,the turbulence strength becomes weak with increasing the distance from measurement points to grid position,becomes strong withincreasing vibration frequency and vibration stokerespectively as power f unction.At the meanti me,the turbulence strength of t wo different grids was co mpared.Fro m the results we know that the length of grid has great influence on turbulence strength,this is different fromthe turbulence characteristic in a water box.
wave tank;oscillating grid;turbulence
P731.26
A
0253-4193(2017)12-0012-08
马洪余,戴德君,乔方利,等.波浪水槽中振动格栅湍流特征的实验研究[J].海洋学报,2017,39(12):12-19,
10.3969/j.issn.0253-4193.2017.12.002
Ma Hongyu,Dai Dejun,Qiao Fangli,et al.An experimental study on characteristics of turbulence generated by oscillating grids in a wave tank[J].Haiyang Xuebao,2017,39(12):12-19,doi:10.3969/j.issn.0253-4193.2017.12.002
2017-01-03;
2017-04-11。
海洋上层混合过程参数化及实验验证(2016YFC1401403);国家自然科学基金项目(41276035,40876015);国际合作项目“海洋动力系统和多运动形态相互作用”(GASI-IPOVAI-05)。
马洪余(1981—),男,山东省枣庄市人,助理研究员,博士,主要从事湍流混合与数值模式参数化研究。E-mail:mahy@fio.org.cn
*通信作者:戴德君(1973—),男,山东省枣庄市人,研究员,博士,主要从事内波混合研究。E-mail:djdai@fio.org.cn

