基于变分多参数正则化方法融合卫星散射计资料
张凯峰,邓婉月,王挺,王慧鹏,项杰,4*,宋清涛,刘春霞
基于变分多参数正则化方法融合卫星散射计资料
张凯峰1,邓婉月2,王挺1,王慧鹏3,项杰1,4*,宋清涛5,刘春霞6
(1.解放军理工大学 气象海洋学院,江苏 南京211101;2.新疆维吾尔自治区环境监测总站,新疆 乌鲁木齐830011;3.75839部队,广东 广州510510;4.南京大学 中尺度灾害性天气教育部重点实验室,江苏 南京210023;5.国家卫星海洋应用中心,北京100081;6.中国气象局广州热带海洋气象研究所,广东 广州510080)
基于常规三维变分同化(3DVAR)思想和反问题中的正则化技术,提出了适用于风场融合的带正则化约束项的3DVAR方法,在南海海域开展数据融合试验,同时采用模型函数方法确定合理的正则化参数,针对一次台风个例进行了Quik SCAT散射计海面风场数据和华南中尺度模式海面风场数据的融合试验,结果表明采用带正则化约束的3DVAR融合方法,明显消除了常规3DVAR方法融合风场时带来的虚假信息,融合后分析风场以及涡度场和散度场分布均匀,结构清晰,气旋中心显著,且分析场中观测起主导作用;采用信号自由度(DFS)方法对融合方法进行定量评估,发现相对常规3DVAR方法,带正则化约束的3DVAR融合系统中观测数据提供的DFS较多,同时提高了观测场对分析场的影响;基于独立观测资料对融合结果进行检验发现相对华南中尺度模式和常规3DVAR方法的统计结果,带正则化约束的3DVAR方法得到的风场具有最小的均方根误差和最大的相关系数。
3DVAR;正则化;Quik SCAT;信号自由度;模型函数
1 引言
在数值天气预报(NWP)中,初始场是最重要的前提条件,业务NWP中心通常利用资料同化方法来获得一个最优的初始场,常用的方法有三维变分同化(3DVAR)、四维变分同化(4DVAR)等。观测资料的多少是数值预报关注的重点。近年来,卫星遥感技术的发展为全球的观测提供了一种有效的技术手段,高时空分辨率的观测数据丰富了原有的观测网络,特别是资料稀疏的海洋区域,不过,由于极轨卫星观测时间一般与区域模式初始场时间不一致,因此如何合理有效地同化卫星观测资料对于提高数值模式初始场的精度以及数值预报的准确率十分重要,尤其是台风的分析预报。已有研究表明同化卫星遥感资料能够改进台风初始场精度,提高台风强度以及路径的预报准确率[1-4]。
海面风场是区域和全球海洋环流的主要动力,调节海气之间水汽、热量以及物质的交换,影响着海洋天气形势的发展演变过程,因此获取高时空分辨率的海面风场具有重要的研究和应用价值。目前获取海面风场产品主要依赖卫星遥感,主要传感器有微波辐射计、散射计以及高度计,其中只有散射计可以同时提供风速、风向,观测海面风场的散射计有SASS、ESCAT、NSCAT、QuikSCAT 以及近年来陆续发射的ASCAT、HY-2A、OSCAT、Rapid SCAT 等,为全球海洋环境的检测提供了丰富的数据,其中QuikSCAT得到了广泛的应用,不仅有原始的轨道刈幅数据,还有经过处理的规则网格化数据,方便了数据的利用。卫星观测数据的日益增加使得风场数据的融合变得越来越重要,许多学者对于海面风场融合方法也做了相关的研究,主要包括统计方法和变分方法,基于统计插值方法开展风场融合的研究较多,Tang和Liu[5]采用连续订正方法对ERS-1散射计风场和数值天气预报模式风场进行融合,得到了分辨率为1°,12 h一次的风场产品;Royle等[6]基于分层Bayes方法融合了NSCAT散射计和NWP风场,Perrie等[7]采用最优插值法(OI)融合了ERS-2、NSCAT、ERS-2高度计和数值模式风场,得到了西北大西洋天气尺度高分辨率的网格化海面风场数据。Atlas[8]在1993年就利用变分法融合了SSM/I风速资料和ECMWF风场数据,为之后CCMP(Cross-Calibrated Multi-platfor m)数据集的发布提供了基础,Chao等[9]在加州中部海岸开展了Quik SCAT与区域数值模式风场数据的融合,通过与独立观测资料进行对比得出融合风场具有最小的误差和最大的相关性。目前国外已经发布了相关的海面风场融合产品,主要包括CCMP数据集和QSCAT-NCEP混合风场资料,为研究和应用提供了长时间序列的海面风场数据。国内对于风场融合也做了一些相关的研究,为了获取较高时空分辨率的风场,凌征等[10]采用Cressman方法将Quik SCAT风场与气象站风场数据融合,为研究我国近海环流的特征提供了参考,蒋兴伟和宋清涛[11]利用低通滤波方法融合了3种散射计资料,包括NSCAT、Quik SCAT和Seawinds,通过滤波的方式对散射计刈幅扫描数据进行处理,有效消除了卫星数据反演过程中带来的奇异值,并且保留了丰富的中小尺度信息,获得了逐月的风场数据,空间分辨率为0.25°×0.25°。在我国HY-2A卫星发射后,国内学者对其搭载的散射计风场产品也做了相关的融合研究[12-13]。而在南海海域,由于其地形复杂,岛屿较多,近海风场具有十分明显的季风特征和地形特点,国外开发的全球海面风场数据产品未必适合我国临近海域的研究和应用需要,因此,充分利用多源卫星遥感风场数据,开展我国近海海域海面风场数据融合研究十分必要[14]。
由于风场融合问题本质上属于反问题[15-17],而反问题通常是不适定的,因此,开展风场数据融合的研究既具有理论意义,也具有应用价值,求解不适定问题的一个有效途径是正则化方法[16]。已有研究表明,在大气海洋领域,将正则化思想引入到变分同化系统里可以很好的解决不适定问题,通过利用L曲线或者模型函数方法选取最优的单正则化参数,可以提高计算效率,得到了较好的结果[18-20]。本文在常规3DVAR的基础上,利用反问题中的正则化技术开展对南海海面风场数据融合的研究,将Quik SCAT散射计海面风场数据与华南中尺度模式(Guang Zhou Mesoscale Model,GZMM)输出的海面风场数据进行融合,并且采用模型函数方法确定合理的双正则化参数,以得到最佳的融合风场,然后利用信号自由度方法计算带正则化约束的3DVAR融合系统中的信息容量,探讨分析场对观测场的敏感性,最后通过西沙自动气象站独立观测资料对融合结果进行验证,评估融合效果。
2 研究区域以及数据
2.1 研究区域
南海海域及其周边存在较多的岛屿,由于散射计风场反演数据的精度受陆地的干扰较大,为了减少这种影响,选择远离陆地的区域,范围为10.12°~17.92°N,110.12°~117.92°E(图1中的红色方框区域)。在该区域内的永兴岛上,中国科学院南海海洋研究所于2008年建成了西沙海洋观测站,其中包括无人自动气象观测站(AWS,图1中的五角星位置),AWS的海面风场数据可用来进行精度验证。
2.2 数据介绍
2.2.1 独立观测数据
独立观测数据来自西沙永兴岛上的无人自动气象站(AWS)提供的距离海面10 m处的风场,时间范围为2008年8-12月,时间分辨率为2 min,包括风速、风向,其中风向采用16方位角表示,方位序号0~15表示N-NNW,2009年6月之后以度数来表示,所有数据均经过质量控制,剔除明显错误。
2.2.2 Quik SCAT散射计资料

图1 研究区域(红色方框)和AWS位置(五角星)Fig.1 Research area(red box)and AWS location(five-pointed star)
QuikSCAT为太阳同步轨道海洋科学卫星,于1999年6月19日发射,携带了测量海面风场的散射计,运行周期为101 min,刈幅宽度为1 800 k m,工作频率为13.4 GHz,测量距离海面10 m高度的风场,空间分辨率为25 k m,每天可观测的范围覆盖了全球90%的海洋。美国国家航空航天局喷气推进动力实验室(NASA/JPL)发布了两种Quik SCAT L2B风场产品,一种是标准的风场产品,另一种是改进了模糊剔除技术得到的风场产品[21]。Ebuchi等[22]利用太平洋以及大西洋浮标资料对Quik SCAT风场进行验证,得出散射计风场与浮标一致性高,风速、风向均方根误差分别为1.00 m/s和22.4°,精度较高。本文利用改进的模糊剔除技术的Quik SCAT风场产品进行南海海面风场融合研究。
2.2.3 模式风场数据
本文采用的模式数据为华南中尺度模式输出的海面风场数据。GZMM由中国气象局广州热带海洋气象研究所开发,预报模式基于GRAPES_TMM(GRAPES Tropical Mesoscale Model)的非静力平衡模式,同时加入了适应本地的物理过程、地形处理及适合南海的边界层技术方案、热带对流技术方案、水物质技术方案。水平方向采用等距的经-纬格点和Arakawa-C格式,模式的预报范围:10.0°~35.0°N,95.0°~130.0°E。本文所用数据范围为2008年9-12月,模式水平分辨率为0.12°,每日两次(00、12 UTC)预报,分别发布84 h时效的预报,海面10 m风场是其业务产品之一,GZMM并没有同化Quik SCAT风场数据,保证了数据之间的独立性。
2.2.4 数据质量控制
在数据融合之前,必须对Quik SCAT数据进行质量控制,以防引进不良观测信息影响融合结果。首先,根据wvc_qual_flag标识,剔除覆盖陆地以及冰面的数据;Quik SCAT风速设计范围为3~30 m/s,剔除该范围之外的数据。第二,对于降雨标识数据,在分析台风时,由于台风周围降雨数据较多,剔除过多观测数据难以辨别台风中心的位置,并且会影响融合后台风位置以及强度的变化,在融合时保留这些数据[5],非极端天气条件考虑降雨数据的剔除。第三,由于极轨卫星接收资料的连续性,为了充分利用观测资料,融合时间窗口选择3 h。
3 研究方法
3.1 方法介绍
3.1.1 常规3DVAR方法
3DVAR的目的是融合观测数据与背景场。基于以下假设:(1)观测及背景误差服从均值为0的正态分布;(2)观测误差和背景误差不相关,则3DVAR问题归结为如下常规的目标函数的极小化(称为常规的3DVAR):
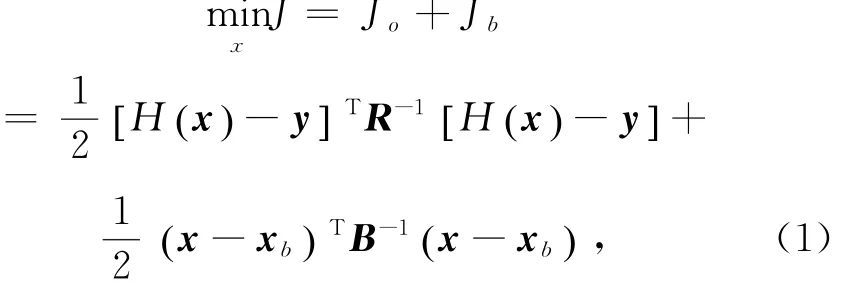
其中,x和xb分别为分析场和背景场;y是观测场;H是观测算子;R和B分别为观测误差协方差矩阵和背景误差协方差矩阵; ( )T和 ( )-1分别表示矩阵的转置和逆。
3.1.2 带正则化约束的3DVAR方法
同化问题本身属于反问题,而B的估计不可避免地含有误差,因此可以引入正则化参数α来修正B;同时,对于风场融合来说,引入的观测风场信息可能在融合后的风场中产生虚假的空间梯度,因此,引入先验的平滑项作为正则化项进行约束[9,23],本文选取风场的涡度梯度和散度梯度作为正则化项加入到目标函数中,表达式为:
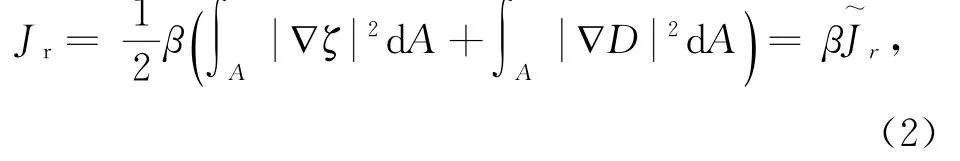
式中,d A=d x d y,β为正则化参数,则常规的目标函数(1)变为:
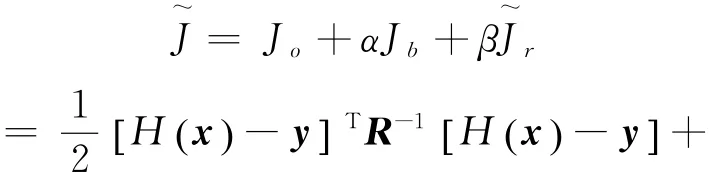
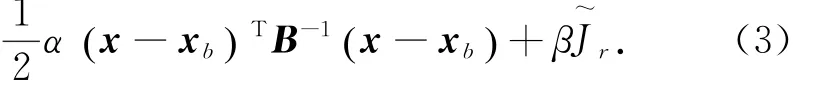
故对于本文要研究的海面风场融合来说,
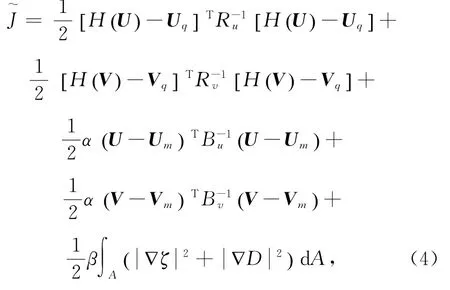
式中,U和V分别为风矢量的纬向和经向分量;下标q和m分别代表Quik SCAT和模式;α、β为正则化参数,ζ和D分别为海面风场的涡度和散度。为了区别,J~的极小化问题称为带正则化约束的3DVAR。在本文中,H取为线性插值算子(双线性插值)。对Jr进行离散处理可得:
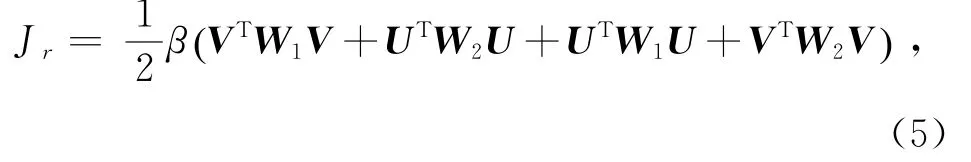
式中,W1=L1TL1,W2=L2TL2,L1和L2为二阶偏导离散后的系数矩阵(详细推导见附录)。本文采用有限内存的拟牛顿法(L-BFGS)实现目标函数的最小化。通过计算可得目标函数(4)的梯度:∇J~=,其中,
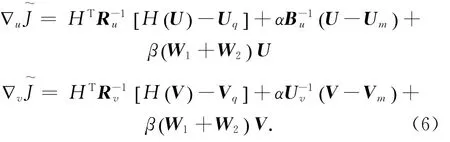
3.1.3 误差协方差矩阵的统计
观测误差协方差矩阵及背景误差协方差矩阵的估计是资料同化的一个重要环节。本文中的B矩阵采用Parish和Derber[24]提出的NMC方法进行计算:
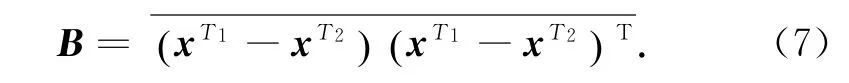
对于区域模式来说,T1和T2一般为12 h和24 h[25]。
观测误差假定是不相关的,则R为一对角矩阵,观测误差方差为对角线元素,则R=σ2I,根据Quik-SCAT与AWS对比结果(图2)可知,U、V的误差方差分别为:
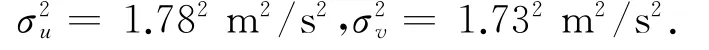
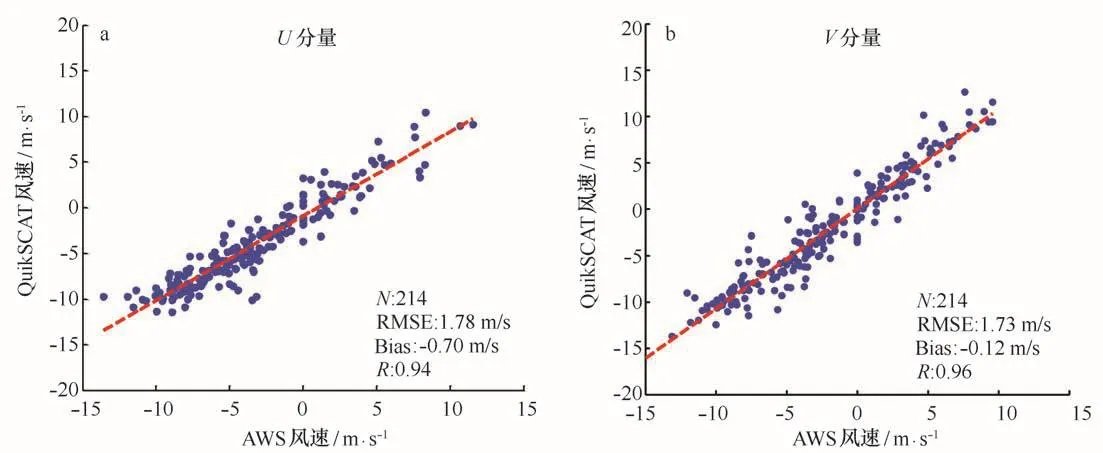
图2 Quik SCAT与AWS风速U、V分量散点图Fig.2 The U and V component scatter plot bet ween QuikSCAT and AWS
3.1.4 正则化参数的选取
选取合适的正则化参数是求解反问题时采用正则化方法的关键,常用的选取方法主要有Morozov偏差原理[26]或吸收Morozov偏差原理、L曲线准则[27]、广义交叉检验准则[28]等,其中Morozov偏差原理或吸收Morozov偏差原理是一种十分有效的参数选取方法,然而利用数值方法直接求解关于正则化参数的非线性方程时往往计算量很大,而且只具有局部收敛性,结果并不令人满意。为了有效求解这样的非线性方程,Kunisch和Zou[29]提出了模型函数方法,一些学者将该方法进行了进一步的研究和发展[30-31],并且将该方法应用到多个正则化参数的选择。下面针对本文要研究的海面风场融合给出一般性的描述。从目标函数(3)可以得到:
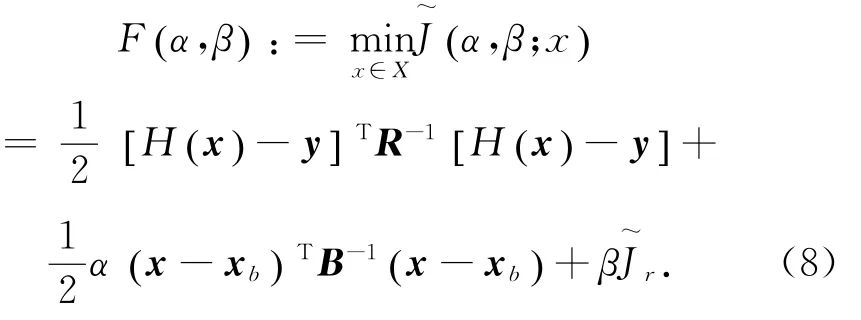
则吸收Morozov偏差方程为:
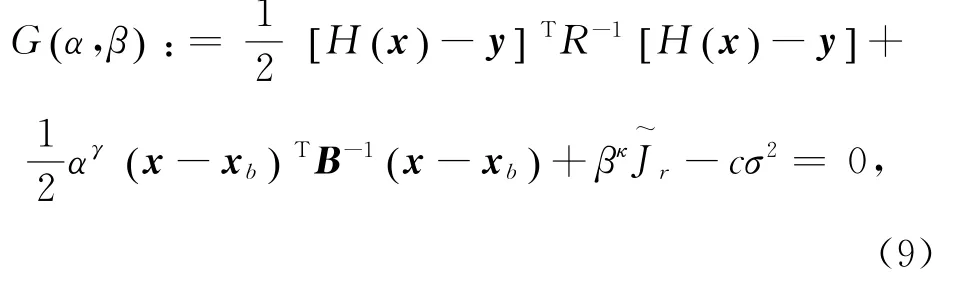
式中,γ>1、κ>1为吸收系数;c≥1为常数;σ为误差水平;式(9)等价于:
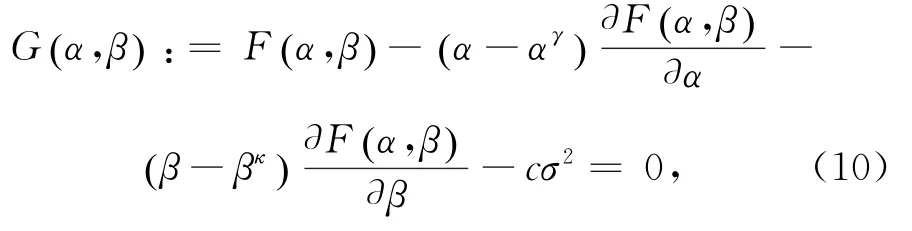
上述方程中Fα,β()没有显示的表达式,且关于α,β是非线性的,因此,采用线性模型函数mkα,β()=Tk+Ckα+Dkβ近似表示Fα,β(),Tk、Ck、Dk为待定参数,代入式(10),则
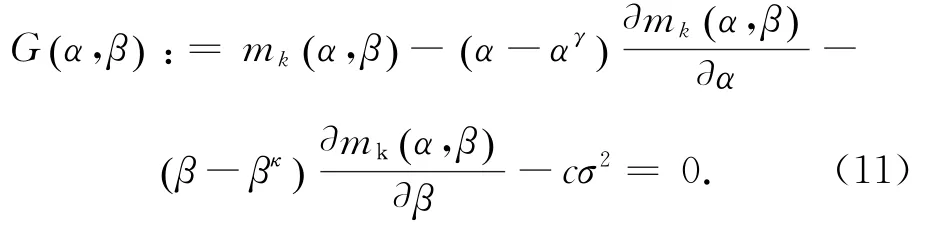
确定双正则化参数的流程图如图3所示。
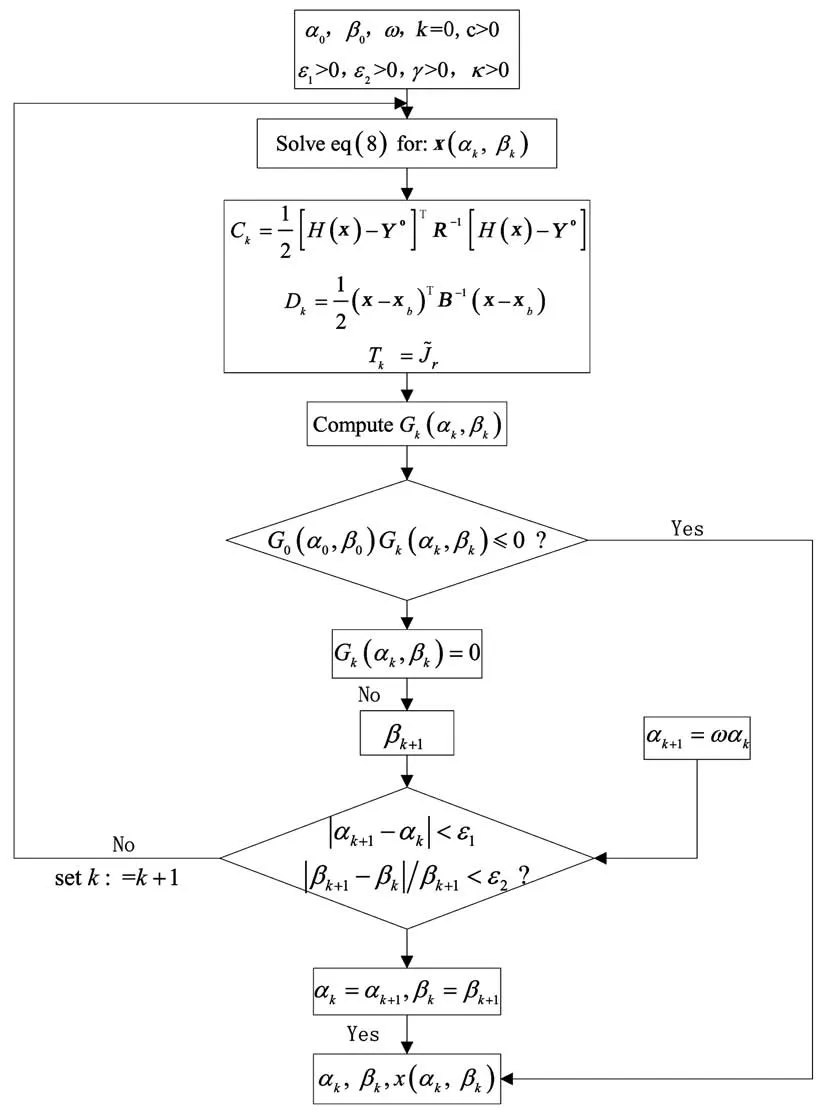
图3 模型函数计算双参数流程Fig.3 Two parameter calculation flow based on model function
3.1.5 信号自由度的计算
信号自由度(DFS)表示一个反演系统(如3DVAR系统)能从观测数据中获得的独立状态变量的数量,同时,它也可以表示同化系统中分析场对观测数据的敏感性,可以用于评估同化或者反演系统[32]。对于常规3DVAR方法来说,最优分析场xa可以表示为:
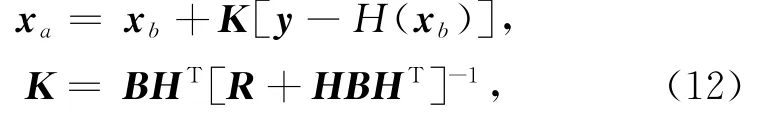
式中,xb是背景场,y是观测场,H是观测算子,K是最优卡尔曼增益矩阵,
H是H在xb附近线性化的切线性算子H=H'(xb)。
同化系统式(12)的DFS定义为:
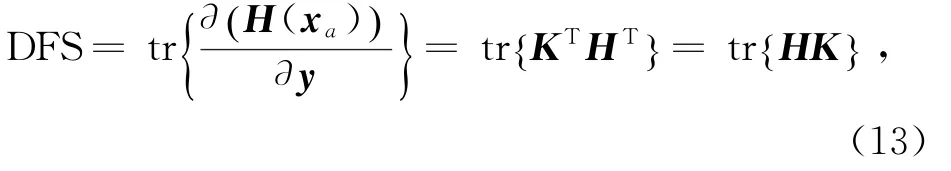
式中,tr{ · }表示 { · }的迹。
而对于带正则化约束的3DVAR模型来说,最优分析xa表示为:
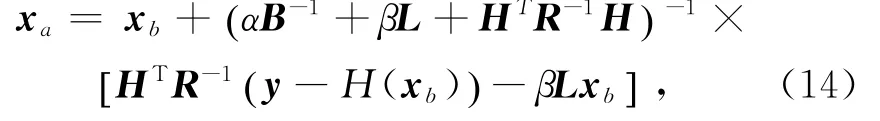
当H为线性算子即H=H时,带正则化约束的3DVAR模型DFS为:
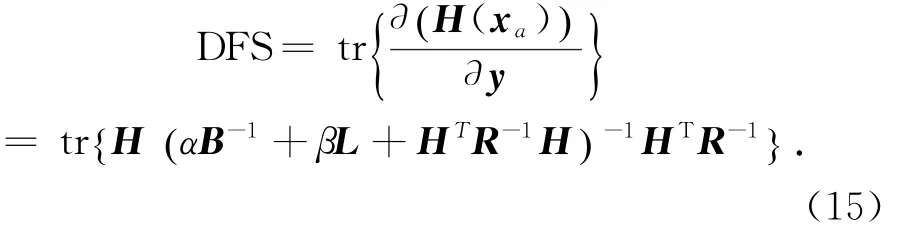
由于本文研究构造的融合系统中,矩阵维数较小,可以直接进行DFS的计算。
3.2 方案设计流程
方案实施流程图如图4所示。首先运用观测场和背景场分别统计观测误差协方差矩阵和背景误差协方差矩阵,并确定观测算子;然后采用拟牛顿法分别求解得到常规3DVAR方法和带正则化约束的3DVAR方法的最优分析场,借助模型函数方法确定合理的双正则化参数,计算信号自由度,对融合系统进行评估;最后利用自动气象站独立观测数据检验融合效果。为了方便,文中将常规3DVAR方法和带正则化约束的3DVAR分别简称为常规方法和正则化方法。
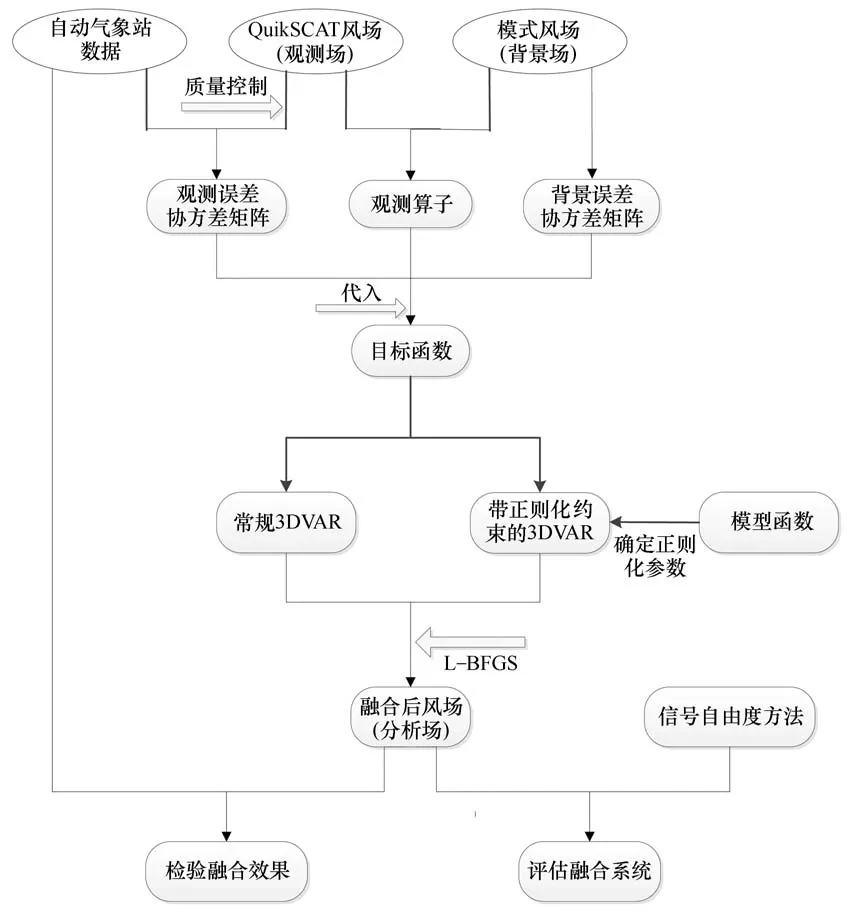
图4 方案设计流程图Fig.4 The flow chart for program design
4 数值试验及结果
4.1 台风个例分析
以2008年第16号台风“米克拉”为例进行融合试验,分析正则化方法的有效性。9月28日,在南海中部海面生成的热带低压,于29日2时正式编报并于8时加强为热带风暴,中心风力8级,风速达18 m/s。以2008年9月28日12时12 h预报场为背景场,9月28日Quik SCAT L2B升轨资料为观测场,融合结果为29日00时分析场,参照中国气象局热带气旋资料中心最佳路径数据集(www.typhoon.gov.cn),29日00时热带风暴中心位置位于16.3°N,111.2°E。图5为观测场和背景场的环流分布形势,图5a为Quik SCAT轨道刈幅观测数据,可以看出,图中有一个明显的气旋环流,但气旋中心不太明显,中心位置大约在16°N,111°E附近,气旋周围风速较大,最大风速在气旋的西南侧,达到28 m/s,位于背景场(图5b)的西北侧;图5b为背景场的环流分布形势,图中气旋性环流明显且中心显著,中心位于15.7°N,112.8°E附近,最大风速达到16 m/s,位于气旋中心的东南侧。
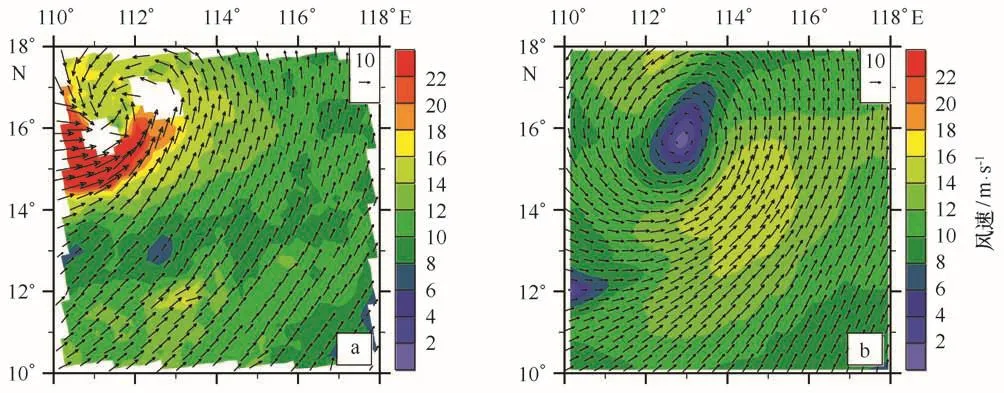
图5 2008年9月28日QuikSCAT观测场(a)与背景场(b)环流形势Fig.5 Quik SCAT observation field(a)and background field(b)circulation distribution in September 28,2008
为了显示正则化约束的作用,做如下试验:β=0和β≠0分别研究单参数以及双参数对融合结果的影响。令β=0分析调节α对融合结果的影响,设计了3组试验,即α=1,α=0.1,α=0.01分析融合结果,如图6所示。
定义均方根误差(RMSE):
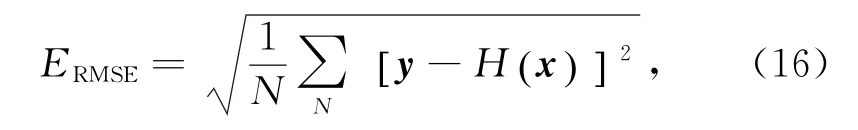
式中,y为Quik SCAT观测场;H为观测算子;当x=xb时,即为观测场与背景场之间风速的RMSE;x=xa时为观测场与分析场之间风速的RMSE;N为观测个数。通过计算融合卫星散射计前观测场与背景场(O-B)以及融合后观测场与分析场(OA)之间的差异,分析观测信息对分析场的影响。
表1为观测与背景和观测与分析之间的均方根偏差RMSE,以及相应的Jo与Jb的数值,后者反映了分析场与观测场以及背景场偏差的大小。当Jo>Jb时,分析场主要由背景场确定(即分析场接近背景场),当Jo<Jb时,分析场主要由观测场确定。
当α=1时,即为常规方法,所得到的分析场如图6a所示。从图6a可以看出,融合Quik SCAT散射计观测资料之后,分析场的热带气旋中心位置及强度有了明显的改变(相对背景场来说),气旋环流中心接近于观测,并且最大风速变大,但是,分析场(融合后的风场)分布不均匀,风场涡度场和散度场分布散乱,不规则,存在许多异常的小范围涡度低值区和散度高值区,并没有体现出气旋中心,可见融合Quik SCAT风场的同时,引入了虚假的观测信息,增加了分析场的噪声;另一方面,虽然O-A的RMSE为2.49 m/s小于O-B的RMSE值,为3.15 m/s,但是,Jo>Jb(表1),这表明分析场接近于背景场,背景场起主要作用。随着α减小,O-A的RMSE也逐渐减小,Jo与Jb的值变化显著:Jo的值从大变小,Jb的值从小变大,并且,热带气旋周围风速大值区域逐渐变大,涡度高值区和散度低值区变化显著;当α=0.01时,O-A的RMSE减小为1.98 m/s,Jo的数值为3 386.535明显小于Jb的值(18 623.01),这表明分析场更接近于观测场,观测场起主要作用,但从涡度场和散度场的分布可以看出,通过调整正则化参数α,分析场的涡度场及散度场散乱现象没有改变,虚假噪声并没有得 到有效的抑制,难以确定涡度、散度中心。
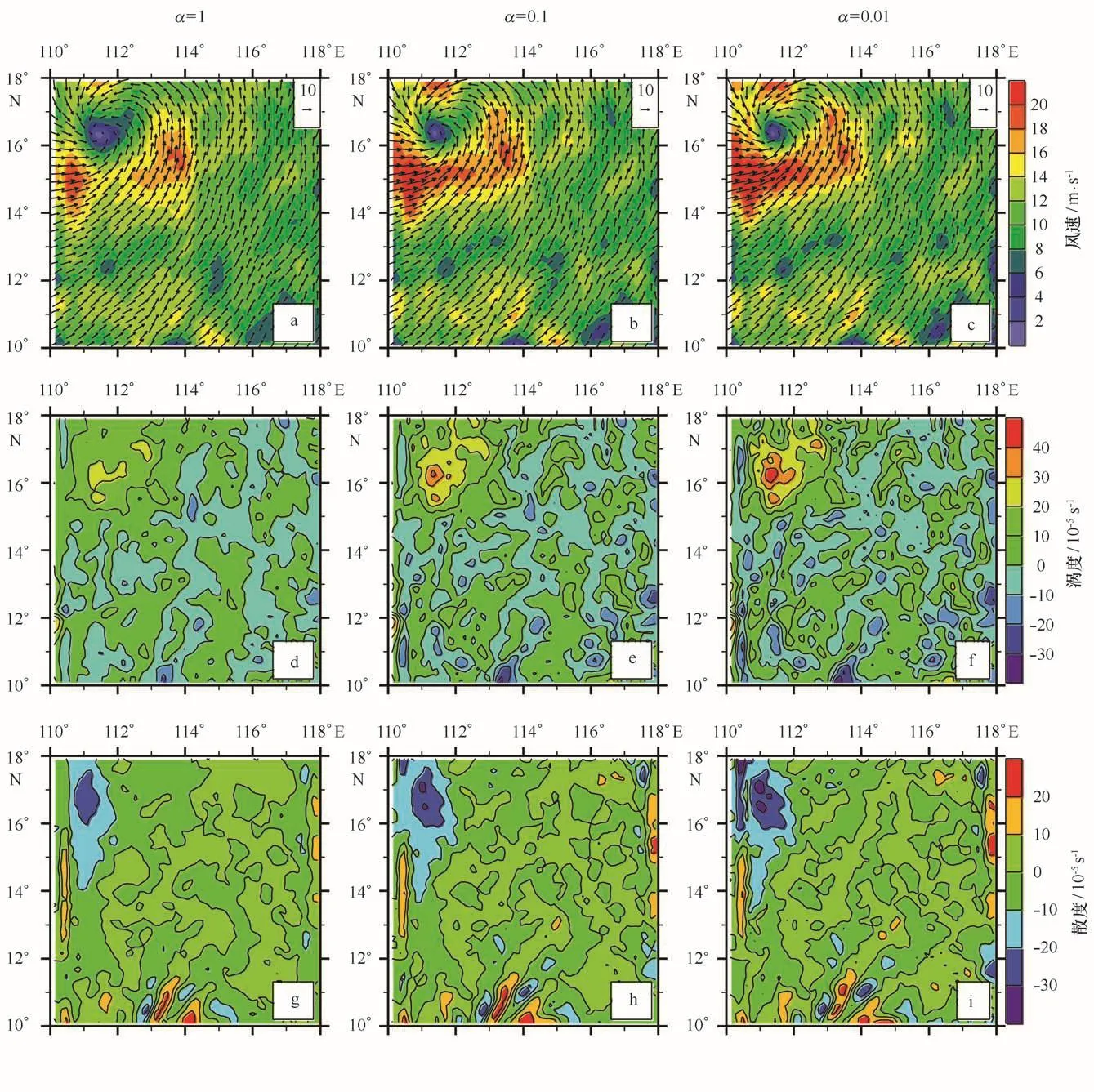
图6 α=1(a,d,g),α=0.1(b,e,h)以及α=0.01(c,f,i)时分析风场(a~c)、涡度场(d~f)和散度场(g~i)分布Fig.6 The distribution of wind field(a-c),vorticity(d-f)and divergence(g-i)whenα=1(a,d,g),α=0.1(b,e,h)andα=0.01(c,f,i)

表1 β=0时O-B和O-A的RMSE以及J o与J b的数值变化Tal.1 The RMSE of O-B and O-A as well as the value of J o and J b whenβ=0
为了克服这一现象,引入先验的平滑约束项来调整风场,即β≠0,通过调节目标函数J~中的正则化参数α、β,以得到最优的融合风场。利用模型函数方法可得合理的双正则化参数分别为α=0.002,β=3.30,相应的融合后风场如图7a所示。与常规方法得到的分析风场相比,正则化方法得到的整个环流场分布均匀,涡度场(图7b)和散度场(图7c)变化显著,明显消除了图6d~6i中涡度场和散度场出现的异常低值和高值区域,分布均匀,结构清晰,可以辨认热带气旋涡旋中心的大概位置,位于16.4°N,111.5°E附近,平滑约束项对风场融合引进的虚假噪声进行了有效的抑制,O-A的RMSE为1.79 m/s,分析场主要依赖于观测场,达到了融合的目的。
试验分析结果表明,不考虑平滑约束项即β=0时,通过调节单参数α改变分析场中观测场和背景场的主导作用:α越小,分析场越接近于观测场,观测场起主要作用,背景场得到了有效地抑制,但分析风场噪点较多,涡度场和散度场出现了异常的低值和高值区域,结构异常散乱,热带气旋中心也不显著;在风场融合系统中加入先验的平滑约束后,通过确定合理的双正则化参数对分析风场进行调整,可以得出,正则化方法进一步改善了融合效果,有效消除了风场融合时出现的噪点现象,明显改善了分析风场以及涡度和散度场的分布情况,风场的涡度场和散度场分布更加均匀,结构清晰,热带气旋中心十分显著,中心位置与实况更加接近,融合后气旋的结构和强度均优于散射计风场、模式风场以及运用常规方法融合得到的结果,且观测场与分析场风速的均方根误差最小,正则化方法有效融合了观测信息。
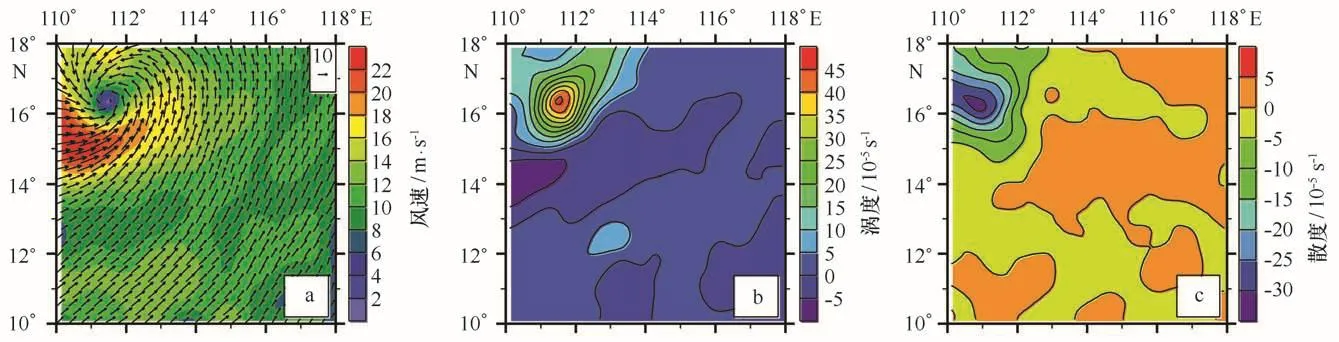
图7 正则化方法的分析风场(a)、涡度场(b)和散度场(c)Fig.7 Analysis of wind field(a),vorticity field(b)and divergence field(c)of regularization method
4.2 敏感性分析
下面利用信号自由度(DFS)方法分别计算常规方法(α=1,β=0)和正则化方法(α=0.002、β=3.30)中U和V分量的DFS,考察分析场对观测数据的敏感性(或观测数据对分析场的影响),并且对比分析两种方法之间的差异。Lupu等[33]指出,对于任意选定的资料,可以用观测影响(OI)表述观测数据对分析场的平均影响,即:
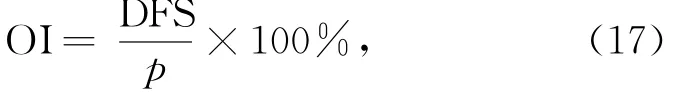
式中,p为观测数量。这里针对本文的情形计算相应的OI,计算结果见表2。

表2 信号自由度和观测影响Tab.2 Signal freedomand observation influence
从表2可以看出,常规方法融合系统中,U风速 和V风速提供的DFS分别为37.284 2和34.754 8,观测场对分析场的影响OI分别为3.25%和3.03%,观测对分析的影响较小,而在正则化方法融合系统中,观测提供的DFS增大,分析场中包含的观测信息量明显增加,U分量和V分量提供的DFS分别变为85.562 7和85.082 9,观测数据对分析场的影响相对常规方法也有了明显的改变,其中U分量的观测影响(OI)从3.25%增加到7.46%,V分量的OI从3.03%增加到7.42%,增加了大约4%,可见经过正则化约束提高了融合系统的信息容量,增强了分析场对观测数据的敏感性。
5 融合效果评估
利用常规方法以及正则化方法分别进行长时间的融合试验,选取数据融合的时间范围为2008年9月26日至11月25日共两个月,将Quik SCAT散射计二级风场的升轨和降轨数据(观测场)分别与GZMM模式风场数据(背景场)进行融合,利用公式(16)分别统计每天升轨和降轨的观测与背景以及观测与分析的均方根误差,评估引入观测信息对模式初始场的影响以及不同融合系统所得结果之间的差异,并且基于独立的观测数据,对融合结果进行验证,检验融合效果。
图8为长时间序列的升轨和降轨融合结果中风速的O-A和O-B的风速RMSE变化趋势,其中黑色虚线表示观测场与背景场的RMSE,蓝色虚线和红色实线分别为观测场与常规方法融合分析场以及观测场与正则化方法分析场的RMSE,在一个成功的同化系统中,O-A的RMSE应小于O-B。从图8可以看出,数据融合前观测场与背景场差异较大,RMSE在2~4 m/s之间波动,波动幅度较大,融合Quik SCAT散射计资料之后,RMSE变化显著,O-A的RMSE明显小于O-B,且大部分数值在2 m/s以下,表明融合后观测场接近于分析场,观测起主导作用,而利用正则化方法的融合效果更好,O-A的RMSE均小于常规方法的统计结果,升轨(图8a)和降轨(图8b)的结果一致。
基于独立的西沙自动站观测数据,对融合效果进行评估,通过以下几个统计量进行检验,统计结果见表3。定义A为对比数据,B为参考数据,N为匹配样本量。
平均值(Mean):
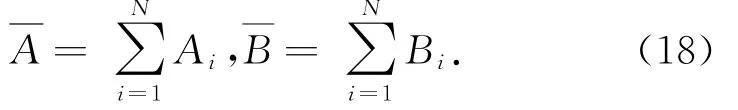
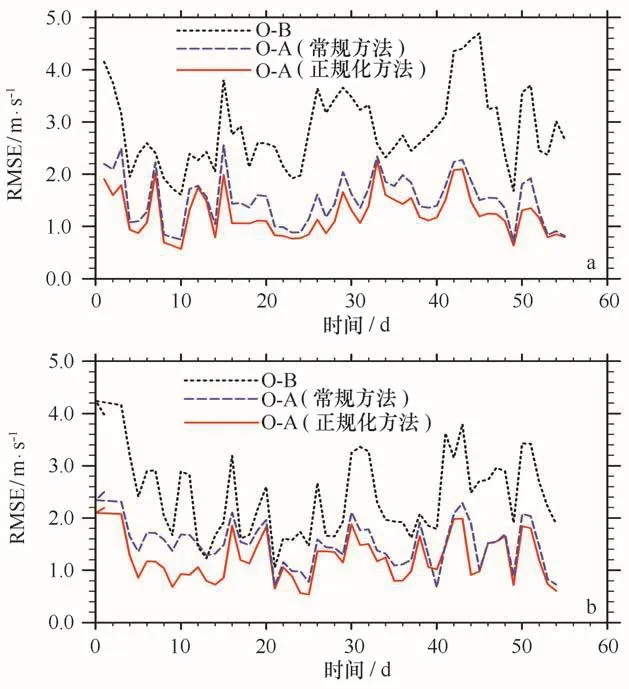
图8 升轨(a)和降轨(b)的O-A和O-B的RMSE变化序列Fig.8 The RMSEseries of O-A(a)and O-B(b)for ascend(a)and descend(b)respectively
平均偏差(Bias):
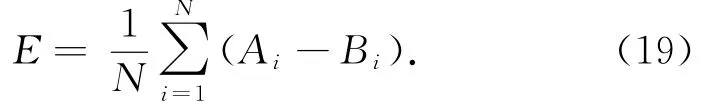
均方根误差(RMSE):
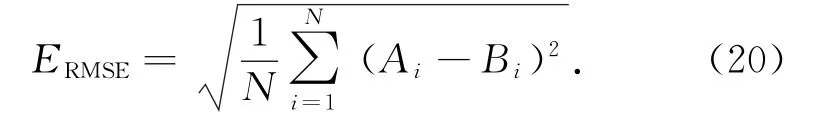
相关系数(R):
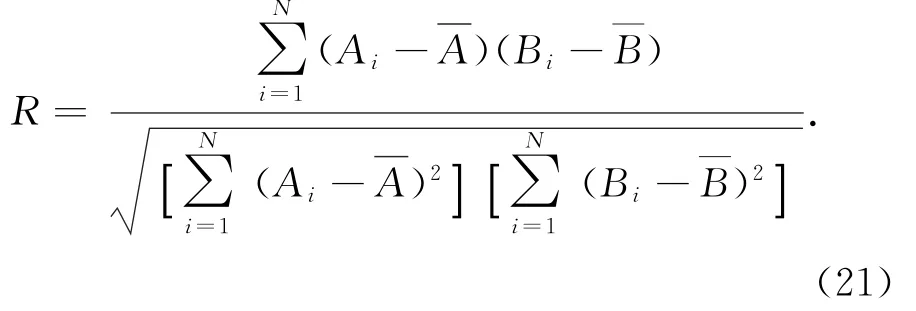
从统计分析结果可以看出(表3),观测误差,即Quik SCAT风速RMSE为1.68 m/s,与设计精度保持一致,U、V分量RMSE也均在2 m/s以内,与自动站一致性好,相关系数在0.92以上;背景场风速相对自动站风场偏差比较大,风速RMSE为2.26 m/s,U、V分量均方根误差分别为2.55 m/s和2.34 m/s,U分量相关性较差;利用常规的3DVAR方法融合后,分析场风速以及风速分量相对背景场统计结果有所改善,风速RMSE为2.07 m/s,U分量相关性提高比较显著,相关性达到了0.85;而正则化方法融合结果风速以及风速分量精度变化显著,风速RMSE为1.92 m/s,其中V分量精度的变化较大,RMSE减小到1.96 m/s,相关性达到0.94,与独立观测数据一致性高。可见融合QuikSCAT散射计观测数据后,风场的精度相对GZMM模式精度有了明显的改善,其中采用正则化方法得到的风场具有最小的均方根误差和最大的相关系数。
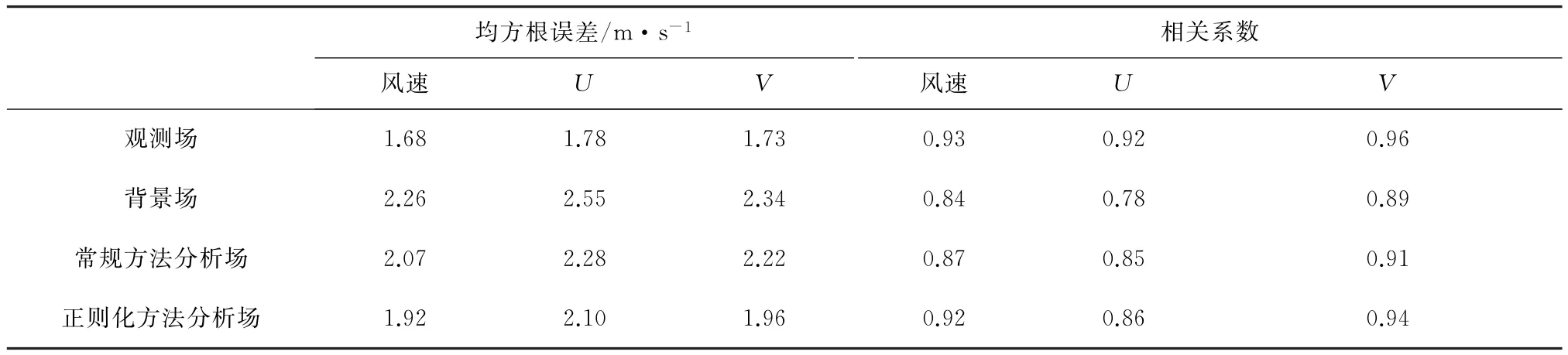
表3 统计对比结果Tab.3 The results of statistical comparison
6 结论和讨论
本文主要利用正则化方法在南海海域开展了卫星散射计(Quik SCAT)和区域中尺度模式(GZMM)风场资料的数据融合试验,并采用模型函数方法选取合理的双正则化参数,针对一次台风个例以及长时间序列融合试验验证了正则化方法的有效性,并对融合结果进行了检验和评估,具体如下:
(1)个例融合结果发现常规方法得到的分析风场中噪点较多,涡度场和散度场分布异常散乱,难以辨认气旋中心,而采用正则化方法后,明显消除了常规方法融合风场时带来的虚假信息,风场以及涡度场和散度场中的噪点现象基本消失,分布均匀,结构清晰,热带气旋中心显著,相对于模式与实况更加接近,且Quik-SCAT观测场与融合后分析场的均方根误差明显小于其与背景场的统计结果,达到了融合的目的,同时正则化方法融合系统中观测数据提供的DFS较多,观测对分析的影响较强,经过正则化约束后,观测对分析的影响大约增加了4%,增强了分析对观测的敏感性。
(2)采用西沙永兴岛自动站观测资料对长时间序列的融合结果进行检验,得出GZMM模式U和V分量均方根误差分别为2.55 m/s和2.34 m/s,相关性分别为0.78和0.89,常规方法U和V分量均方根误差分别为2.28 m/s和2.22 m/s,相关性分别为0.85和0.91,正则化方法融合结果中分析场U和V分量均方根误差分别为2.10 m/s和1.96 m/s,相关性分别为0.86和0.94,优于GZMM模式和常规方法融合的统计结果,因此融合Quik SCAT观测资料后,对背景场的影响比较明显,U分量和V分量的精度和相关性都得到了改进,正则化方法得到的分析场具有最小的均方根误差和最大的相关系数。
通过台风个例和长时间序列的融合试验检验结果发现正则化方法是合理有效的,不过在台风个例融合试验中为了体现正则化方法的优势,并没有考虑降雨对散射计数据的影响,因此在后续的工作中需要改进质量控制方案,对数据进行合理的处理,并进一步验证正则化方法的普遍性,为开展我国周边海域的风场融合研究提供参考。
致谢:感谢国家科技基础条件平台——国家地球系统科学数据共享平台——南海及其邻近海区科学数据中心(http://ocean.geodata.cn)提供数据支撑,感谢中国气象局广州热带海洋气象研究所提供的GZMM(Guang Zhou Mesoscale Model)模式资料,感谢美国NASA喷气推进实验室(JPL)提供的Quik SCAT风场资料。
[1] Zou Xiaolei,Xiao Qingnong.Studies on theinitialization and si mulation of a mature hurricane using a variational bogus data assi milation scheme[J].Journal of the At mospheric Sciences,2000,57(6):836-860.
[2] Chen S,Vandenberghe F,Petty G W,et al.Application of SSM/I satellite data to a hurricane si mulation[J].Quarterly Journal of the Royal Meteorological Society,2004,130(598):801-825.
[3] Chen Shuhua.The i mpact of assi milating SSM/I and QuikSCAT satellite winds on Hurricane Isidore si mulations[J].Monthly Weather Review,2007,135(2):549-566.
[4] Singh R,Pal P K,Kishtawal C M,et al.Thei mpact of variational assi milation of SSM/I and Quik SCAT satellite observations on the numerical si mulation of Indian Ocean tropical cyclones[J].Weat her and Forecasting,2008,23(3):460-476.
[5] Tang Wenqing,Liu W T.Objective Interpolation of Scatterometer Winds[M].California:JPL Publication,1996.
[6] Royle J A,Berliner L M,Wikle C K,et al.A hierarchical spatial model for constructing wind fields fro m scatterometer data in the labrador sea[M]//Case Studies in Bayesian Statistics.New York:Springer,1999:367-382.
[7] Perrie W,Dunlap E,Vachon P W,et al.Marine wind analysis from remotely sensed measurements[J].Canadian Journal of Remote Sensing,2002,28(3):450-465.
[8] Atlas R.A multiyear global surface wind velocity dataset using SSM/I wind observations[J].Bulletin of the American Meteorological Society,1996,77(5):869-882.
[9] Chao Yi,Li Zhijin,Kindle J C,et al.A high-resolution surface vector wind product for coastal oceans:Blending satellite scatterometer measurements with regional mesoscale at mospheric model si mulations[J].Geophysical Research Letters,2003,30(1):1013.
[10] 凌征,王桂华,陈大可,等.中国近海风场融合[C]//中国“数字海洋”论坛论文集.天津:国家海洋信息中心,2008:90-94.Ling Zheng,Wang Guihua,Chen Dake,et al.China's offshore wind field fusion[C]//China's“Digital Ocean”Foru m Proceedings.Tianjin:National Mariti me Infor mation Centres,2008:90-94.
[11] 蒋兴伟,宋清涛.海洋卫星微波遥感技术发展现状与展望[J].科技导报,2010,28(3):105-111.Jiang Xingwei,Song Qingtao.Satellite microwave measurements of the global oceans and f uture missions[J].Science&Technology Review,2010,28(3):105-111.
[12] 齐亚琳,林明森.数据融合技术在海洋二号卫星数据中的应用[J].航天器工程,2012,21(3):117-123.Qi Yalin,Lin Mingsen.Application of the data fusion techniquein HY-2 satellite data[J].Spacecraft Engineering,2012,21(3):117-123.
[13] 刘宇昕,张毅,王兆徽,等.基于ASCAT微波散射计风场与NCEP再分析风场的全球海洋表面混合风场[J].海洋预报,2014,31(3):10-18.Liu Yuxin,Zhang Yi,Wang Zhaohui,et al.Global sea surface blended winds based on the scatterometer winds and NCEPreanalyzed winds[J].Marine Forecasts,2014,31(3):10-18.
[14] 项杰,王慧鹏,王春明,等.南海海面风场变分融合的初步研究[J].热带气象学报,2015,31(2):153-160.Xiang Jie,Wang Huipeng,Wang Chun ming,et al.Preli minary study on variational blending of surface vector windsin South China Sea[J].Journal of Tropical Meteorology,2015,31(2):153-160.
[15] 肖庭延,于慎根,王彦飞.反问题的数值解法[M].北京:科学出版社,2003.Xiao Tingyan,Yu Shengen,Wang Yanfei.Numerical Solution of Inverse Problem[M].Beijing:Science Press,2003.
[16] 刘继军.不适定问题的正则化方法及应用[M].北京:科学出版社,2005.Liu Jijun..The Regularization Method and Application of Unsuitable Problem[M].Beijing:Science Press,2005.
[17] Wang Wanqiu,Xie Pingping.A multiplatfor m-merged(MPM)SST analysis[J].Journal of Cli mate,2007,20(9):1662-1679.
[18] 姜祝辉,黄思训,杜华栋,等.利用变分结合正则化方法对高度计风速资料调整海面风场的研究[J].物理学报,2010,59(12):8968-8977.Jiang Zhuhui,Huang Sixun,Du Huadong,et al.A new approach to adjusting sea surface wind using altimeter wind data by variational regularization method[J].Acta Physica Sinica,2010,59(12):8968-8977.
[19] 赵延来,黄思训,杜华栋,等.正则化方法同化多普勒天气雷达资料及对降雨预报的影响[J].物理学报,2011,60(7):875-886.Zhao Yanlai,Huang Sixun,Du Huadong,et al.Regularization method of assi milating Doppler radar data anditsinfluence on precipitation forecast[J].Acta Physica Sinica,2011,60(7):875-886.
[20] Wang Sicheng,Huang Sixun,Xiang Jie,et al.Three-di mensional ionospheric tomography reconstruction using the model function approach in Tikhonov regularization[J].Journal of Geophysical Research:Space Physics,2016,121(12):12104-12115.
[21] Jet Propulsion Laboratory.Quik SCAT science data product user's manual,Version2.22001[EB/OL].[2016-10-09].daac,jpl.nasa.gov/quikscat/qscat doc.ht ml
[22] Ebuchi N,Graber H C,Caruso MJ.Evaluation of wind vectors observed by QuikSCAT/Sea Winds using ocean buoy data[J].Jour nal of At mospheric and Oceanic Technology,2002,19(12):2049-2062.
[23] Hoff man R N,Leidner S M,Henderson J M,et al.At wo-di mensional variational analysis met hod for NSCAT ambiguity removal:Methodology,sensitivity,and tuning[J].Journal of At mospheric and Oceanic Technology,2003,20(5):585-605.
[24] Parrish D F,Derber J C.The National Meteorological Center's spectral statistical-inter polation analysis system[J].Mont hly Weather Review,1992,120(8):1747-1763.
[25] 曹小群,黄思训,张卫民,等.区域三维变分同化中背景误差协方差的模拟[J].气象科学,2008,28(1):8-14.Cao Xiaoqun,Huang Sixun,Zhang Wei min,et al.Modeling background error covariance in regional 3D-VAR[J].Scientia Meteorologica Sinica,2008,28(1):8-14.
[26] Kunisch K.On a class of damped Morozov principles[J].Computing,1993,50(3):185-198.
[27] Hansen P C,O’Leary D P.The use of t he L-curvein the regularization of discreteill-posed problems[J].SIA MJournal on Scientific Computing,1993,14(6):1487-1503.
[28] Golub G H,Heath M,Wahba G.Generalized cross-validation as a method for choosing a good ridge parameter[J].Technometrics,1979,21(2):215-223.
[29] Kunisch K,Zou J.Iterative choices of regularization parameters in linear inverse problems[J].Inverse Problems,1998,14(5):1247.
[30] Lu S,Pereverzev S V.Multi-parameter regularization and its nu merical realization[J].Nu merische Mathematik,2011,118(1):1-31.
[31] Wang Z.Multi-parameter Tikhonov regularization and model f unction approach to the damped Morozov principle for choosing regularization parameters[J].Journal of Computational and Applied Mathematics,2012,236(7):1815-1832.
[32] Rodgers C D.Inverse Methods for At mospheric Sounding:Theory and Practice[M].Singapore:World Scientific Publishing Co Pte Ltd.,2000.
[33] Lupu C,Gaut hier P,Laroche S.Evaluation of t hei mpact of observations on analysesin 3D-and 4D-Var based on infor mation content[J].Monthly Weather Review,2011,139(3):726-737.
附录
关于正则化项Jr的处理:
海面风场的涡度ζ和散度D,表达式如下:
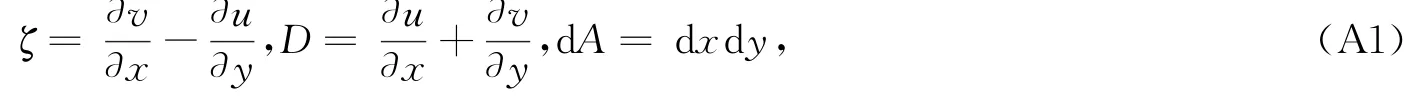
式中,u,v分别为单个网格点的纬向和经向风速,对Jr进行处理可得:
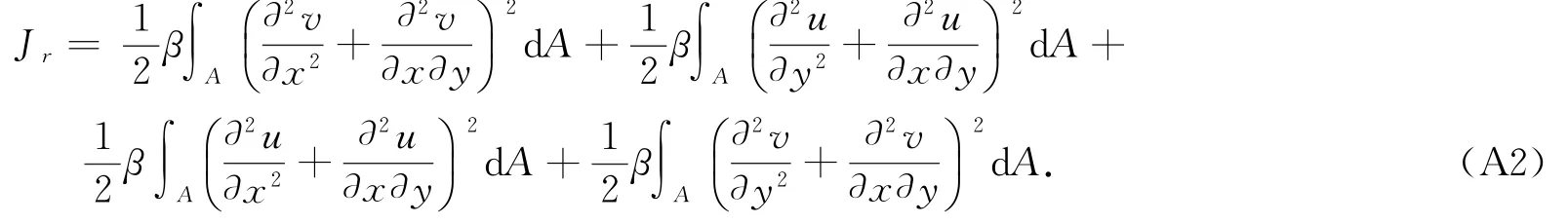
式(A2)可以简化为:
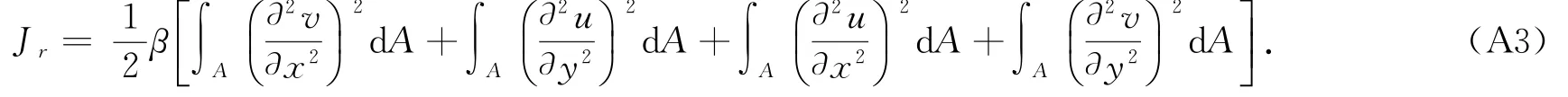
将积分离散化,利用前差法计算二阶偏导,最终可得:
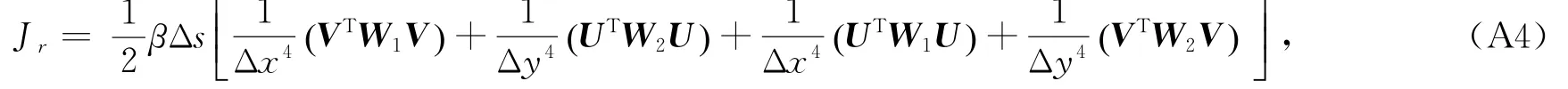
式中,Δs为单个网格面积,W1=L1TL1,W2=L2TL2,L1和L2为二阶偏导离散后的系数矩阵,分别为:

根据本文设计模型,分析风场的分辨率为0.12°×0.12°,因此Δx≈Δy,Δs≈ Δx( )2,将吸收进系数β中,可以得到:
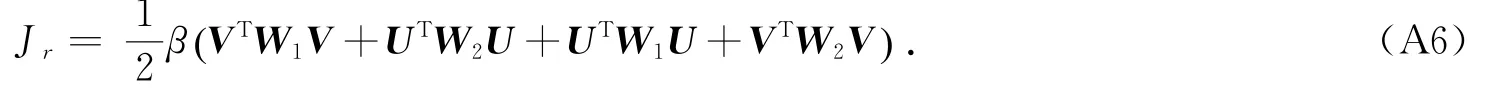
Blending satellite scatterometer data based on variational with multi-parameter regularization method
Zhang Kaifeng1,Deng Wanyue2,Wang Ting1,Wang Huipeng3,Xiang Jie1,4,Song Qingtao5,Liu Chunxia6
(1.Institute of Meteorology and Oceanogr aphy,PLA University of Science and Technology,Nanjing 211101,China;2.Xinjiang Uygur Autono mous Region Environ mental Monitoring Station,Uru mqi 830011,China;3.Unit No.75839 of PLA,Guangzhou 510510,China;4.Key Laboratory of Mesoscale Severe Weather(Nanjing University),Ministry of Education,Nanjing 210023,China;5.National Satellite Ocean Application Ser vice,State Oceanic Ad ministration,Beijing 100081,China;6.Guangzhou Institute of Tropical and Marine Meteorology,China Meteorological Ad ministration,Guangzhou 510080,China)
A 3DVAR method with regularization constraints is proposed to blend sea surface wind datain the South China Sea based on the traditional 3DVAR and regularization technology of the inverse problem,and the model function method which is used to deter mine the reasonable regularization parameters and then the blended experiments of the satellite scatterometer(Quik SCAT)and Guang Zhou Mesoscale Model(GZMM)sea surface wind field data are carried out for a typhoon case.Results show that when we use the regularization method for experiments,the false infor mation caused by the traditional 3DVAR is eli minated obviously and the noiseis al most disappeared,at the same ti me,the wind field and vorticity field as well as divergence field are distributed evenly,and the structure is clear,more i mportantly,it is clear that the cyclone center is remarkable,and observation is dramatic in the analysis field.Besides,the degrees of freedomfor signal(DFS)method is used to evaluate blended systems quantitatively,it is found that the regularized constraint 3DVAR system has a higher DFSand observation influence related to traditional 3DVAR.The blended results are tested based on theindependent observation data,it indicates that the result of regularized constraint 3DVAR method has the s mallest root mean square error and maxi mumcorrelation coefficient,which is better than the statistical result of GZMMand the conventional 3DVAR method.
3DVAR;regularization;Quik SCAT;the degrees of freedomfor signal;model function
P715.6
A
0253-4193(2017)12-0122-14
张凯峰,邓婉月,王挺,等.基于变分多参数正则化方法融合卫星散射计资料[J].海洋学报,2017,39(12):122-135,
10.3969/j.issn.0253-4193.2017.12.012
Zhang Kaifeng,Deng Wanyue,Wang Ting,et al.Blending satellite scatterometer data based on variational with multi-parameter regularization method[J].Haiyang Xuebao,2017,39(12):122-135,doi:10.3969/j.issn.0253-4193.2017.12.012
2017-01-23;
2017-03-16。
国家自然科学基金(41275113);全球变化与海气相互作用专项。
张凯峰(1994—),男,山西省运城市人,主要从事海面风场融合研究。E-mail:15380426538@163.com*通信作者:项杰,男,安徽省巢湖市人,教授,主要从事海面风场融合研究。E-mail:xjieah@aliyun.com

