龙门式焊接机器人制动过程的动力学特性优化

蔡玉强，朱东升

(华北理工大学 机械工程学院，河北 唐山 063210)

龙门式焊接机器人制动过程的动力学特性优化

蔡玉强，朱东升

(华北理工大学 机械工程学院，河北 唐山 063210)

龙门式焊接机器人；ANSYS Workbench；模态分析；动力学分析

某厂生产的龙门式焊接机器人快速制动时振动严重，焊枪处的振幅最大可达10.32 mm，振动衰减慢，无法保证焊接精度。针对这个问题，基于ANSYS Workbench软件对焊接机器人的龙门架结构进行了模态分析，并采用对龙门架的Y轴横梁施加加速度的方法分析了其制动过程的动力学特性，发现联接部件与Y轴横梁的连接处为薄弱环节。根据分析结果，对龙门架结构进行了优化，优化后的分析结果表明：机器人焊枪处振动的最大振幅为1.68 mm，比优化前降低了83.6%，振动衰减速度明显加快，达到了现场焊接精度要求。

龙门式焊接机器人是直角坐标机器人的一种，具有行程较大、负载载荷大、运行平稳、支撑刚性较好等特点[1]。但是，由于机器人和Y轴横梁等运动部件质量较大，机器人在快速制动时会对龙门架造成冲击，使整个龙门架结构产生振动。龙门架结构尺寸很大,对微位移的放大效果非常显著,从而造成机器人焊枪的振动幅度过大，严重影响焊接精度和使用效率。因此，研究龙门式焊接机器人的动力学特性对提高机器人的焊接精度具有重要的指导意义。

目前，国内外学者对各种形式的龙门结构的动力学特性进行了研究。许丹等[2]通过动态测试和参数辨识方法获得了龙门式加工中心横梁的导轨结合面特性参数，并将其应用到横梁滑箱系统整体的有限元模型中,经过模态分析得到系统固有频率和各阶振型图。张君、朱海涛等[3]设计了一种用于装配作业的十字龙门式机器人，结合机器人的特点，通过设计大刚度的龙门结构，来提高系统的刚度和精度。

国外，C.S.Teo等[4]基于拉格朗日方程建立了三自由度的H型龙门桁架结构的动力学模型。并用自适应控制装置最大化的降低了轨迹误差和轴间偏移误差。Huijie Zhang等[5]考虑了轴耦合力对滑块导轨节点刚度的影响,用混合单元法建立了龙门式机床行走横梁的等效动力学模型，研究了滑块导轨节点刚度的变化和行走横梁的固有频率。N.D.Zrnic′和V.M.Gas^ic′等[6]研究了承受悬架动载荷的龙门式起重机构，通过结合有限元法和解析法建立运动方程，获得了龙门式起重机构的动力学响应。

目前，国内关于龙门式结构的研究大多数只进行了模态分析，得到了系统的各阶振型图。有的只是通过加大龙门结构的刚度来提高系统的精度，并没有对其动力学特性进行研究和优化。该项研究针对某厂生产的龙门式焊接机器人在快速制动过程中机器人振动严重的问题，通过对焊接机器人的龙门架结构进行模态分析和动力学分析得到了龙门架结构的六阶模态振型和动力学特性曲线。根据分析结果对龙门架和横梁的结构进行了改进，优化后结构的动力学特性达到了现场实际的焊接精度要求。

1 龙门式焊接机器人的系统构成

为了方便分析，对焊接现场的龙门结构进行了模型简化。如图 1 所示，坐标系方向如图,4个立柱固定在地面上，Y轴横梁5位于龙门架2上，实现X轴方向移动。Y轴横梁5上有移动平台，联接部件3和配重4位于移动平台上，实现Y轴方向移动。操作臂6安装在联接部件3上，位于横梁左侧，实现Z轴方向移动，横梁右侧为配重，用于平衡操作臂，防止横梁变形。操作臂的末端是焊接机器人7，实现焊接功能。机器人X、Y、Z轴方向的移动都是通过伺服电机驱动，齿轮传动。根据现场实测和观察，由于配重的质量和Y轴横梁的跨度比较大，相当于单摆结构，易造成横梁变形。操作臂依靠联接部件5与Y轴横梁联接，因此行走横梁和联接部件的变形大小会直接影响机器人的焊接精度。

图1 龙门式焊接机器人的简化模型

2 龙门架结构的动态分析

2.1 模态分析

对龙门架4个立柱底部的法兰施加固定约束后，用ANSYS Workbench软件对其进行模态分析，共提取六阶模态，如表1所示。

表1 各阶模态频率

在此只列出变化比较大的第五、六阶模态，如图2所示。

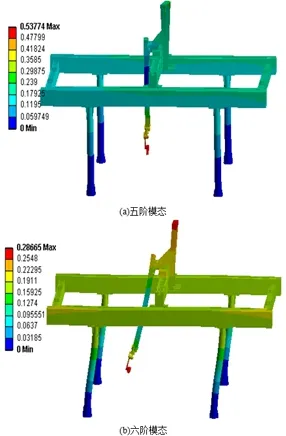
图2 第五、六阶模态

通过对图2分析发现，第五阶模态的固有频率为5.08 Hz.最大变形出现在机器人处，且整个龙门架有向X轴负方向变形的趋势。第六阶模态固有频率为5.69 Hz。最大变形出现在机器人焊枪处和配重顶部，联接部件附近变形明显，且与第五阶模态相比，整个龙门架向X轴负方向变形的趋势增大。所以进行优化时考虑取消配重，修改联接部件结构。并且对龙门架与立柱的结构进行改进，提高整体结构的稳定性。

2.2 瞬态动力学分析

2.2.1有限元法求解动力学方程[8]

三维弹性动力学基本方程:

平衡方程

(1)

几何方程

(2)

物理方程

σi,j=Dijklεkl

(3)

边界条件

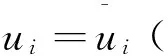
(4)

(5)

ANSYS Workbench采用离散空间域的方法来求解动力学方程，构造的插值函数为：

u=Nαe

(6)

其中，N为形函数矩阵，与时间无关，节点参数ae为时间的函数。

将平衡方程(1)及力的边界条件(4)的等效积分形式用Galerkin提法表示：

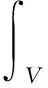
(7)

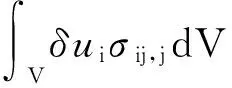
(8)

将离散后的位移表达式(5)代入上式，最终得到系统的求解方程：

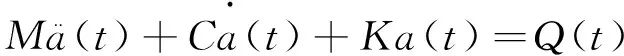
(9)

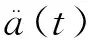
在任意时间t内，方程可看作是一系列考虑了惯性力和阻尼力的静力学平衡方程。ANSYS Workbench使用Newmark时间积分法在离散的时间点上求解这一系列方程。

2.2.2施加加速度载荷

结构的动力学响应可以看作是各阶模态响应的组合，时间步长应足够小，小到能够解出对龙门架整体响应有贡献的最高阶模态。ANSYS Workbench使用的是Newmark时间积分方法，在最高阶模态的频率的每个周期内取20个点就可以得到比较合理精度的解[9]。即:

(10)

式中：Δt为积分时间步长

f为频率

根据提取的六阶模态结果可知，对龙门架整体响应有贡献的最高阶模态是第六阶模态。由公式(10)得，时间步长Δt=0.008 8 s。

不少学者在实验的基础上,给出了钢结构的阻尼比的经验值范围[10]：其中焊接结构取ξ=0.008～0.01，铆接结构取ξ=0.015～0.05。根据现场的实际结构，本文动力学分析的阻尼比取0.05。当Y轴横梁以最大速度运动时，电机快速制动的加速度为2 m/s2。加速度曲线如图3所示，方向为X轴正向。

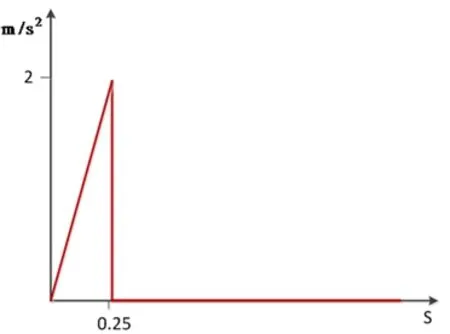
图3 加速度曲线

2.2.3 分析结果

Y轴横梁的停止位置为龙门架中间位置，移动平台处于Y轴横梁的中间位置，焊接机器人处于下极限位置。此时整个系统的振动对焊枪精度的影响最大。龙门架整体的位移响应结果如图3所示。

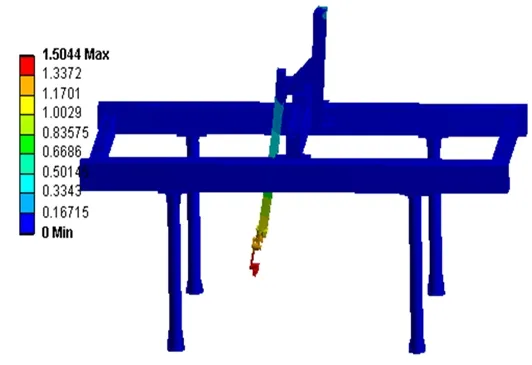
图4 龙门架整体位移响应

由图4可以看出，振动幅度最大的位置出现在操作臂和机器人焊枪处。于是提取机器人焊枪的位移响应如图5、图6所示。

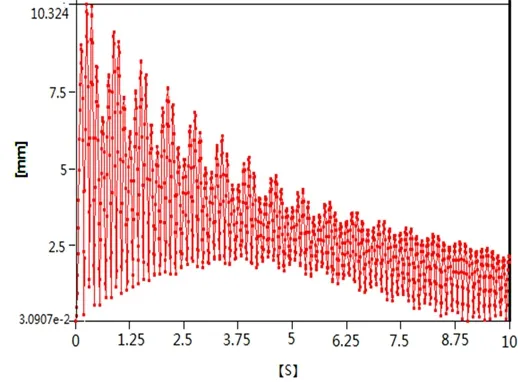
图5 机器人焊枪总位移响应

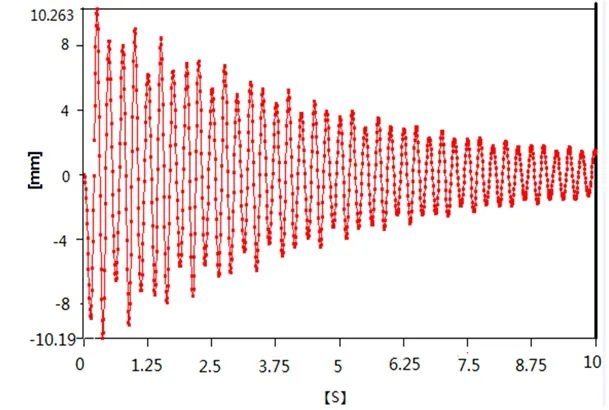
图6 机器人焊枪X方向位移响应

通过对图5分析可知，机器人焊枪振动最大幅度为10.32 mm。由于加速度为+X方向，所以机器人焊枪主要在X方向振动。分析图6可知，在X正方向的最大振幅为+10.26 mm。在X负方向的最大振幅为-10.19 mm。可以看出机器人焊枪振动严重，导致机器人无法正常工作，因此必须对龙门架的动力学特性进行优化。

3 龙门架结构的优化

根据第五、六阶模态和动力学的分析结果，对龙门架结构进行优化设计。优化后的模型如图7所示。

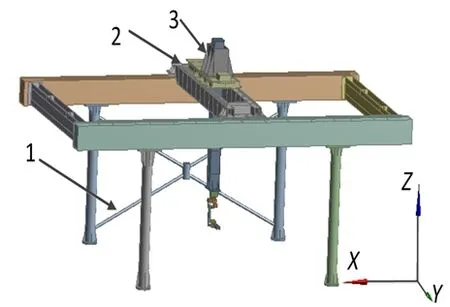
图7 龙门架结构优化设计后模型

为了提高龙门架结构和Y轴横梁的稳定性，在立柱的非进料口一侧增加了连接架。把单侧梁改为了双侧梁，减轻横梁的扭转变形。取消了配重，增加了滑箱。连接架和横梁的结构如图8所示。

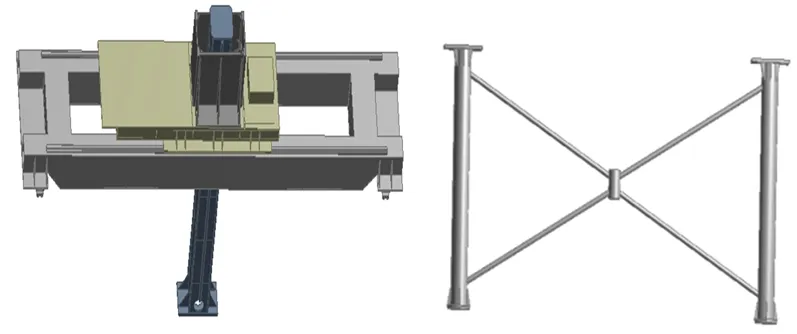
图8 横梁和连接架

4 优化后龙门架的动力学分析

对优化后的模型进行模态分析，由分析结果可知，对龙门架整体响应有贡献的最高阶模态是第五阶模态，频率为5.759 Hz。如图9所示。

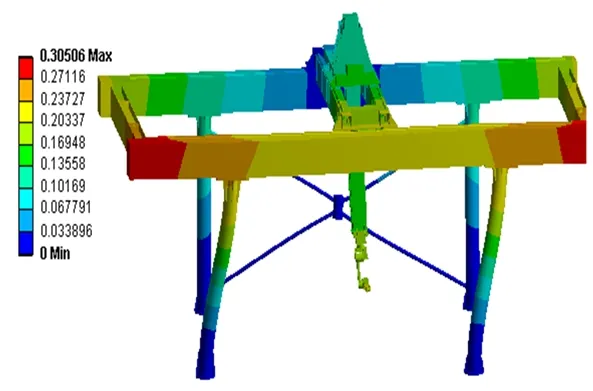
图9 优化后模型的第五阶模态

根据公式(10)求得时间步长Δt=0.008 7 s，其它设置不变。机器人焊枪的位移响应如图10、图11所示。

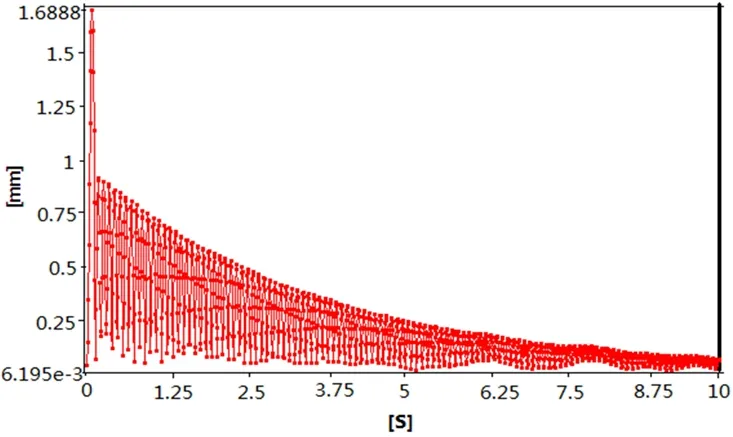
图10 优化后机器人焊枪总位移响应

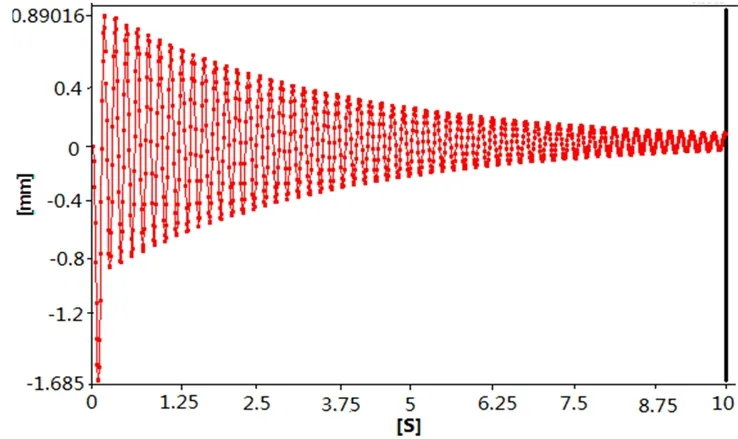
图11 优化后机器人焊枪X方向位移响应

对图10分析可以看出优化后机器人最大振幅为1.68 mm。比优化前降低了83.6%。由图11可得，在X正方向的最大振幅为+0.89 mm。在X负方向的最大振幅为-1.68 mm。分别比优化前降低了91.3%和83.4%。优化后焊接精度得到了大幅度提高，而且焊枪振动的衰减速度明显加快，满足了现场的焊接要求。

5 结论

(1)对龙门式焊接机器人的整体结构进行了模态分析和动力学分析。根据第五、六阶模态结果发现了联接部件处为龙门架的薄弱环节，配重结构会使操作臂和机器人振动加剧。经过对龙门架结构施加加速度载荷，得到了Y轴横梁快速制动时龙门架结构的动力学响应。发现机器人焊枪振动的最大振幅为10.32 mm。严重影响机器人的焊接精度，因此必须对龙门架的动力学特性进行优化。

(2)对龙门架的动力学特性进行了优化。在立柱的非进料口一侧增加了连接架，把单侧梁改为了双侧梁，取消了配重，增加了滑箱。对优化后的模型进行了动力学分析，结果显示，机器人焊枪振动的最大振幅降低了83.6%，振动的衰减速度大幅度提高。达到了实际焊接要求。

[1] 赵玉信.基于直线运动单元的直角坐标机器人系统的研究[D].济南:齐鲁工业大学,2014.

[2] 许丹,刘强,袁松梅，等.一种龙门式加工中心横梁的动力学仿真研究[J].振动与冲击,2008,27(2):168-171.

[3] 张君,朱海涛，谭定忠.十字龙门式机器人的研究[J].机器人技术,2007,(1)：116-118.

[4] C.S.Teo,K.K.Tan,S.Y.Lim,etal.Dynamic modeling and adaptive control of a H-type gantry stage[J].MECHATRONICS,2007，(17): 361-367.

[5] Huijie Zhang,Wanhua Zhao,Chao Du,et al.Dynamic modeling and analysis for gantry-type machine tools considering the effect of axis coupling force on the slider-guide joints' stiffness[J].Journal of Engineering Manufacture, 2015，(9):1-10.

[6] N.D.Zrnic′,V.M.Gas^ic′,S.M.Bos^njak.Dynamic responses of a gantry crane system due to a moving body considered as moving oscillator[J].Archives of Civil and Mechanical Engineering,2015，(15):243-250.

[7] 王勖成.有限单元法[M].北京:清华大学出版社,2003.

[8] 刘笑天.ANSYS Workbench结构工程高级应用[M].北京:中国水利水电出版社,2015.

[9] 孙守胜.龙门起重机金属结构动力学研究[D].武汉:武汉理工大学,2008.

DynamicCharacteristicsOptimizationofBrakingProcessofGantry-typeWeldingRobot

CAI Yu-qiang, ZHU Dong-sheng

(College of Mechanical Engineering, North China University of Science and Technology, Tangshan Hebei 063210, China)

gantry-type welding robot; ANSYS Workbench; modal analysis; dynamic analysis

A gantry-type welding robot produced by a factory has serious vibration problem. When suddenly brake, the maximum amplitude of welding torch can reach 10.32 mm and vibration attenuation rate is slow. In order to solve this problem, modal analysis was conducted by ANSYS Workbench and dynamic analysis was carried out by applying acceleration on the Y axis beam. Based on the result, the connection position of join component and Y axis beam was weak. Structure improvement was carried out. The improved results show that the maximum amplitude of welding torch of robot is 1.68 mm. It was 83.6% lower than before, attenuation of vibration has quickened significantly. The dynamic characteristics of robot meet the requirement of welding precision.

2095-2716(2017)04-0052-08

2017-05-03

2017-09-22

TH113.1

A