人教版与翰林版化学教材中金属晶体相关计算比较*

杨建明

人教版与翰林版化学教材中金属晶体相关计算比较*

杨建明

金属晶体的内容及相关知识是高中化学的难点，其重要性不言而喻，但是金属晶体的堆积方式与其他晶体不同，其抽象性和复杂性使学生理解时不易掌握要点，突破此类试题需要学生具有很强的观察能力以及三维空间想象能力。在人教版金属晶体内容教学中，可以借助翰林版化学教科书的相关插图，展示直观立体的金属晶体堆积模式以降低知识点难度，分析3种堆积模式下有关计算的对策，以利于提高教学效益。

人教版；翰林版；高中化学教科书；金属晶体插图；晶体计算

“物质结构与性质”作为高中化学新课程的一个选修模块，侧重于帮助学生了解人类探索物质结构的重要意义和基本方法，研究物质构成的奥秘，认知物质结构与性质之间的关系。由于该模块知识理论性较强，比较抽象，要求学生有很好的抽象概括能力和空间想象能力，才能形成更好的理解。物质结构的学习不应该仅仅是抽象的概念和难以捉摸的微观空间结构，而应该是明晰生动、形象直观的。教材的插图能展现物质内部的结构特点，将肉眼无法观察的微观世界清晰地呈现在学生面前，这比教师的千言万语都来得更直接、更具体。

一、插图的作用

插图作为传播学习信息的一种重要媒介，已不再是可有可无的点缀，而是表达学习内容和学习方法的重要部分，它对激发学生学习兴趣，充分发掘大脑思维潜能，加速记忆有着纯语言无法比拟的优势。日本学者保坂荣之介经过多年不懈的努力，用大量翔实的事实证明了一个鲜为人知的道理，即人脑中语言信息量与形象信息量之比为1:1 000，人脑对诸如图片等形象信息的记忆能力是语言文字记忆的1 000倍。对于中学阶段化学教学来说，抽象的概念很多，合理利用教材插图，可以活化教学内容，图解困难概念，有魅力的插图可以为教学插上翅膀。

二、人教版与翰林版化学教材的相关插图对比

台湾翰林出版事业股份有限公司出版的《高中选修化学(上)》(简称翰林版)以表格的形式展示金属晶胞简单立方、体心立方以及面心立方3种堆积模型的相关内容，包括堆积方式、配位数、晶胞所含原子数、空间利用率等。在“单位格子”这一栏中清晰地表示出简单立方和面心立方的原子半径与晶胞面对角线之关系(如图1所示)。此外，对于体心立方的原子半径与体对角线的关系则由图2单独展示。

图1

图2

人民教育出版社出版的《高中化学实验教科书》(简称人教版)物质结构与性质则分开展示金属晶胞三种堆积方式。由二维平面的两种堆积模型—非密置层堆积和密置层堆积过渡到三维空间的堆积模型，相邻非密置层原子的原子核在同一直线的堆积方式形成的一个晶胞是一个立方体，每个晶胞含一个原子，为简单立方堆积(如图3所示)。如果是非密置层上的金属原子填入下层的金属原子形成的凹穴中，每层均照此堆积，得到空间利用率比简单立方堆积高很多的体心立方堆积(如图4所示)。

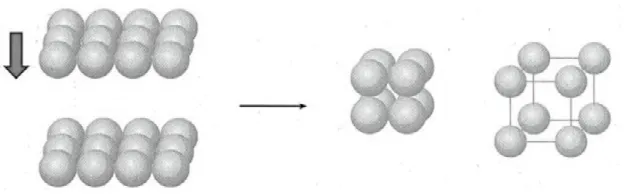
图3

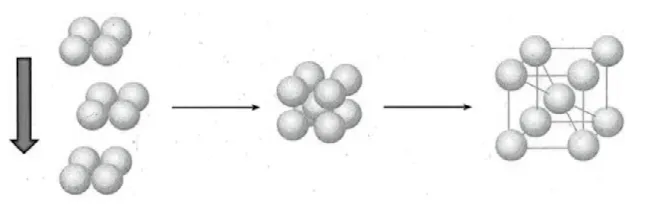
图4

密置层原子按图4堆积方式堆积，会得到两种基本堆积方式，六方最密堆积和面心立方最密堆积，分别为ABABABAB……堆积方式、ABCABCABC……堆积方式(如图5所示)。

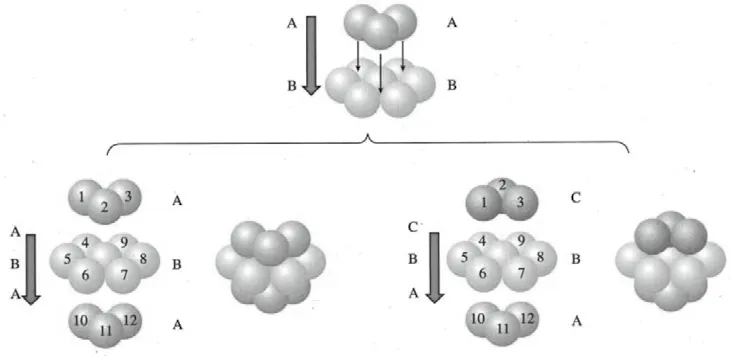
图5

通过对比发现，翰林版化学教材中插图所传递的信息更加丰富，立体感更强，能更加直观地展示3种堆积方式的异同，易于理解较为复杂抽象的空间结构，学生通过观察插图能了解不同堆积方式的配位数、晶胞所含原子数、原子半径与晶胞边长的关系。在教学时，教师可以利用图1和图2列公式演示空间利用率的计算，从而为晶胞密度、体积、阿伏伽德罗常数、边长、粒子间的距离的计算打下基础。

人教版化学教材的侧重点在于通过二维平面的堆积方式呈现三维空间结构，但在实际教学中发现，学生三维空间想象能力有限，通过观察插图依然无法准确获知3种堆积方式中原子半径与晶胞边长之间的关系，在进行有关计算时困难重重。

三、翰林版教材插图在金属晶体有关计算中的运用

晶体的相关计算一直是高考的热点之一，特别是金属晶胞在计算时要结合晶胞的空间构型，考查学生的观察力和想象力，计算较为复杂，学生常会出错。此类试题就成为一类难度大、综合性强的题型，有较好的区分度。利用翰林版教材中的插图可以较为快速简洁地计算出高考常考的3种堆积模型的空间利用率、晶胞密度、晶胞边长等。

空间利用率是指原子体积与晶胞体积的百分比，用它来表示紧密堆积的程度，又叫空间占有率，根据堆积模型不同进行计算。

表1 金属晶体3种堆积模型对比

1.简单立方堆积

在立方体的八个顶点各有一个原子的这种堆积方式称为简单立方堆积，其相邻的原子皆互相接触(如图6所示)。根据均摊法可知晶胞含1个原子，配位数为6，空间利用率为一个原子的体积与晶胞体积之比，密度为一个原子的质量与晶胞体积之比。

图6

设原子半径为r，晶胞边长为a，a=2r，原子为刚性小球，其体积为。晶胞为立方体，其体积为。

则简单立方堆积空间利用率为

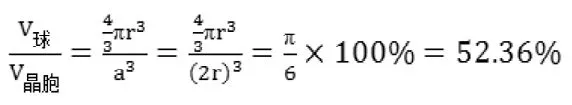
2.体心立方堆积

此堆积方式形成的晶胞亦为一个立方体，位于体对角线的3个原子互相接触(如图7所示)。每个晶胞含2个原子，即粒子数N=2，配位数为8，其空间利用率比简单立方堆积高很多，许多金属是这种堆积方式，如Na，K，Fe，Cr，Ba等。

图7

则体心立方堆积空间利用率为

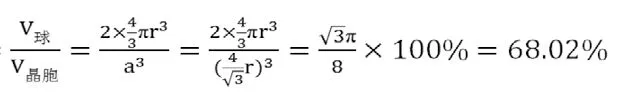
3.面心立方堆积

面心立方堆积的方式为立方体的中心及顶点各有一个原子，此种堆积中，位于各面的对角线上3个原子互相接触(如图8所示)。根据均摊法，每个晶胞含有4个原子，空间利用率比体心立方的高，如Ca，Sr，Al，Ni，Cu等均采用这种堆积方式，配位数为12。

图8

则体心立方堆积空间利用率为

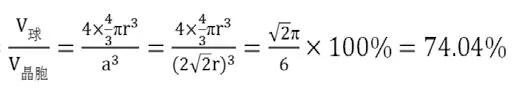
四、试题解析

1.例题1

金属钨晶体中晶胞的结构模型如图9所示。它是一种体心立方结构。实际测得金属钨的密度为ρ，钨的相对原子质量为M，假定钨原子为等直径的刚性球，请回答下列问题：

图9

(1)每一个晶胞均摊到________个钨原子；

(2)晶胞的边长a为____________；

(3)钨的原子半径r为________(只有体对角线上的各个球才是彼此接触的)；

(4)金属钨原子形成的体心立体结构的空间利用率为____________。

【解析】

(3)钨晶胞的体对角线上的各个球彼此接触；

2.例题2

Al单质为面心立方晶体，其晶胞参数a＝0.405 nm，晶胞中铝原子的配位数为______。列式表示Al单质的密度_________g·cm-3(不必计算出结果)。

【解析】Al为面心立方晶体，配位数为12，依据均摊法含有Al原子数目为：

在进行金属晶体有关计算时，先分析其堆积方式，通过均摊法可得出每个晶胞所含粒子数N，再分析不同堆积方式中原子半径r与晶胞边长a之间的关系，便可快速准确地列出晶胞密度、空间利用率、晶胞体积、阿伏伽德罗常数等计算式，从而得出计算结果。

(致谢：本文得到贵州省雷山县第三中学潘国荣老师的指导，在此表示感谢！)

[1]简玉阑.选修化学:上[M].台湾:翰林出版事业股份有限公司,2015.

[2]宋心琦.普通高中课程标准实验教科书·化学·选修3[M].北京:人民教育出版社,2009.

[3]李臣之,周业勤.怎样提高教材中插图的功效[J].教学与教材研究,1996,(3):42-43.

[4]王显成.中学中常见的晶体结构计算[J]. 数理化学习:高中版,2004(5):47-50.

[5]何萍.晶体结构与性质难点测查及对策研究[J]. 高中数理化,2016(2):50.

杨建明，本科，中教二级。贵州省雷山民族中学，557100

本文系2014年贵州省教育科学规划课题专项课题《大陆人教版与台湾翰林版现行高中化学教材的比较研究》(编号：2014GZ042)系列成果之一。