基于数值模拟和波形分析的声发射传感器安装策略
顾爱军,韩文钦
(1.扬州大学水利与能源动力工程学院,江苏 扬州 225127;2.江苏理工学院材料工程学院,江苏 常州 213001)
基于数值模拟和波形分析的声发射传感器安装策略
顾爱军1,韩文钦2
(1.扬州大学水利与能源动力工程学院,江苏 扬州 225127;2.江苏理工学院材料工程学院,江苏 常州 213001)
为提高声发射检测中信号采集的质量,以实现可靠的损伤识别,采用数值模拟方法研究混凝土构件中开裂损伤与声发射信号之间的定量关系。通过对信号的波形分析得到信号的传播特性,以确保信号清晰、稳定为原则,确定传感器的安装准则,包括避开圣维南区域、避开不合理方位、尽量靠近声源等。同时明确当发生较大程度开裂时,传感器位置的影响可忽略。该研究可为实际声发射检测中传感器的安置和声发射信号的损伤诊断提供理论基础。
声发射;数值模拟;传感器安装策略;波形分析;信号特性
0 引 言
混凝土是现代土木工程中用途最广的建筑材料之一。由于外部荷载以及自然灾害、化学侵蚀等各种不利因素的影响,混凝土结构常发生损伤、开裂等现象,使结构性能发生退化,甚至引起灾难性的破坏。因此结构安全问题不容忽视,对重大工程结构及关键构件进行健康监测与损伤诊断显得极为重要。在各类无损检测方法中,声发射技术利用结构材料损伤时发出的弹性波信号进行损伤判别,只需适当布置传感器即可实现对整个结构的监测,不但克服了大型结构的检测困难,还具有实时、动态、在线检测等独特的优势,因而成为工程结构损伤检测领域的研究热点,在混凝土结构健康监测中显示出巨大的潜力。
材料在损伤过程中由于能量瞬间释放而产生的瞬态弹性波(即声发射,AE)反映了材料的损伤特性,因此通过分析AE信号可实现对声源 (损伤)的识别。然而系统所采集的AE信号受传播介质(材料)、结构形式、传感器与接收系统以及环境噪声的影响后发生了显著变化,给声发射检测带来一定的困难。为提高声发射技术损伤识别的准确性和可靠性,常通过大量的理论和实验研究探寻声源机理、提取信号规律,并试图建立AE信号与声源机理的关系[1-4]。然而在混凝土领域,由于干扰因素的复杂性,这一研究尚未取得稳定、可靠、实用的成果。
声发射技术的主要目的是实现损伤的定位、定性和定量检测。在损伤定位中,通常将传感器规律性地分布安装[5],通过各传感器所接收的AE信号并按照特定的算法进行计算反演。在此过程中,常将信号的传播视为各向同性;同样在对损伤进行定性和定量分析时,也往往忽视传感器位置带来的影响。事实上,材料开裂等损伤显然具有方向性,不同方位的传感器所接收的信号必有差别。此外,传播介质的不均匀性、结构边界对波的反射等因素也将对结构各部位产生不同的影响。因此传感器在不同位置响应的差异不容忽视,对该问题的研究可直接影响AE检测的准确度。
由于实际有限结构中损伤源引起的位移响应并无解析解,早期对AE技术中各项问题的研究多采用实验方法进行对比分析。然而声源机理的不确定性和传感器响应的不一致性导致实验结论的规律性和可靠性受到影响。近年来,一些学者采用数值计算方法对AE信号进行了模拟,从声源、传播及响应等方面研究了声发射的相关特征。杨占才等[6]利用一简单的质量块-弹簧系统对AE事件进行模拟,研究了发动机活塞-缸套磨损过程的声发射机理;Kao等[7]在模拟应变作用下纸纤维复杂结构发出的声信号时采用了质量-弹簧模型结构与声波传播模型相结合的方法;Sause等[8]采用一种内源模型对碳纤维增强塑料板进行了模拟,所得AE波的时频特性与实验信号具有较好的一致性。该模型与地震学中的矩张量声源表示法相似。可见,以基于矩张量的力源模型模拟声发射的激发不但符合损伤的力学机理,而且得到了符合实验的结果,是一种简单而行之有效的方法。
采用数值模拟方法研究声发射对不同位置传感器的响应规律可根据确定的声源信号获得可靠的信号响应。本文基于弹性波理论,以平面四点弯曲混凝土梁为研究对象,采用数值模拟方法研究混凝土开裂损伤与AE信号之间的定量关系。通过对不同接收点AE信号的波形分析,探寻不同位置声发射信号的特性,为现场声发射传感器的安装提供合理方案,也为实际AE信号的损伤诊断奠定理论基础。
1 混凝土开裂声发射数值计算模型
1.1 计算结构和模型简化
基于实际四点弯曲试验的素混凝土梁建立了有限元数值模型,其中梁的尺寸为0.15m×0.18m×1.5m(见图 1(a))。 材料密度取 2 300 kg/m3,弹性模量取25GPa,泊松比取 0.2。
在混凝土中采集的AE波频率在几十千赫兹至几百千赫兹,波长在数厘米的范围内,因而其数值模拟的计算过程需要足够小的计算步长和足够密的单元长度,这使得计算量巨大,无法实现对实际结构的三维数值模拟。为此,本文从3个方面对数值计算进行了简化:
1)均质材料简化。根据弹性波理论,当粗骨料粒径小于波长时,混凝土可视为均质材料,这对更大骨料的混凝土会带来较大误差。因此本文实际只考虑了较小粒径粗骨料的情况。
2)结构简化。包括平面简化和对称结构的半结构简化。其中平面简化使得单元数和计算量大大降低,同时仍可探究传感器位置的响应规律。
3)计算范围简化。由于声发射信号在混凝土材料中传播时其能量按指数规律衰减,因此构件远端边界的反射信号可以忽略。为进一步降低简化模型,将远端一半的混凝土梁体用一宽0.2m的矩形吸收区代替(见图1(b))。当AE波传至吸收区时,能量被逐渐吸收。
在混凝土材料中,AE波的频率常在50~400kHz的超声范围内,为探究声源特征,考虑最高频率达600kHz。若纵波波速为4 000 m/s,则波长最小可达6.67 mm,而横波波速和波长更小,仅为纵波的一半左右。因此,计算中有限元单元长度控制在1mm以内,在加载区域,最大单元长度为0.5 mm,采用平面三角形单元,单元总数为156000。时间步长根据单元长度和波速确定,加载期为5×10-9s,加载完毕后,时间步长放宽为4×10-8s。数值模拟通过COMSOL Multiphysics软件完成。

图1 混凝土开裂声发射数值计算模型
1.2 声发射等效力源
混凝土梁弯曲破坏主要为混凝土单向拉伸破坏,其声发射是一种内源,故采用偶极子作为等效力源。声源力大小的瞬时变化有多种模型,常用各种脉冲函数,如半正弦函数、三角形函数等。这些简单函数使用方便,且均符合声发射源突发性的特征,但力的出现与消失存在突兀(函数曲线不光滑),与实际不符。Ohtsu[9-10]在模拟表面AE源产生的波形时,分别采用了以光滑阶跃函数为位移荷载和以4次正弦函数为力荷载的激励方式,均得到了与宽频传感器采集信号相类似的波形。但阶跃函数只能用于位移荷载,而四次正弦函数相对较为复杂。Hora等[11]采用了一种简单、光滑函数模型,其上升时间相对较短,符合混凝土开裂时突发弹性波的特点,且具有较为丰富的频率成分,其表达式为
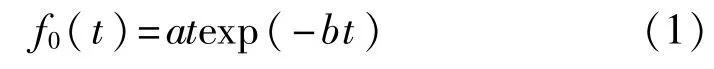
其中a、b为控制声源幅值和持续时间的参数。
本文采用了该力源变化模型,并根据混凝土构件中超声波频带的特点,取a=4×108N/s,b=4×106,使其频带为 0~600kHz。 声源力f0(t)的变化如图 1(c)所示。
由于结构的瞬态响应受结构固有特性的影响,而混凝土开裂必导致整个构件刚度发生变化,为此采用等效弹性模量弱化的方法模拟开裂区裂缝。此处等效弹性模量是混凝土微观开裂损伤所引起的材料宏观弹性性质。开裂发生时开裂区等效弹性模量快速降低,可在施加偶极子力的瞬时使开裂区弹性模量按如下规律变化:

式中:E0——混凝土未损伤时的弹性模量;
Sα(t)——等效弹性模量衰减函数。
按如下规律使等效弹性模量迅速降低至接近0,其计算公式为

式中:t0——控制衰减时间,s;
α——调节衰减速度的无量纲参数。
t0和α可由裂缝扩展速度确定。
2 计算结果
数值模拟研究了不同接收位置、不同开裂程度等与声信号之间的定量关系。其中不同接收位置包含不同接收距离和不同方位的影响;不同开裂程度包括不同开裂长度和不同开裂速度影响。
按裂缝开裂长度可将声源激励分为点源激励和线源激励。初始的微损伤、微开裂或稳定扩展过程中较小的开裂均可视为点源激励,其他各类较长的开裂均视为线源激励。图2为点源激励情况下AE波的传播,其中纵波、横波、表面波以及当纵波传到固体自由表面时由于波型转换产生的头波均明显可见。其中表面波的振幅明显大于其他波形。
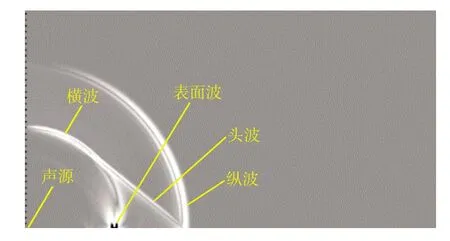
图2 AE波的传播(下边缘位置点源激励)
对线源激励,可将开裂过程视为由若干点源按一定的速度顺序激发。故此时的声源包含了一系列上述复杂的波,其叠加效果受开裂长度、开裂起始位置、开裂速度、接收距离等多种因素的影响。因此,分析各种因素的影响非常必要。
实际应用中,将AE传感器粘附于构件表面,声源激励超声波引起的表面振动信号转变为电信号。由于通常的宽频AE传感器对法向速度νy更敏感[12],因此采用νy随时间的变化作为AE信号以分析其信号特征。此外,AE信号采集的时间起点并非裂缝起裂(声源激励)时间点,而是仿照声发射系统的采集规则进行,即先设定门槛值,该门槛值略小于纵波振幅,使得采集波形以纵波为时间起点。每个信号以2 500 kHz的采样频率采集1 024点,得到时长为0.4096ms的波形。
3 分析与讨论
数值模拟信号所受的影响因素较少,信号波形也相对简单直观。这不但有利于研究不同位置的信号规律以便指导传感器的安装,同时有助于了解不同声源的信号特征以便损伤识别时采取相应的应对措施。
3.1 不同接收位置对声发射信号的影响
声发射检测中的首要任务是获取真实有效的AE信号。因此,了解AE信号的变化规律,确定传感器的最佳安装位置对检测工作具有重要意义。
1)不同接收距离对声发射信号的影响
单点开裂是最为简单的声源形式,此时的AE信号相对单一,所受干扰最小,因此可用于研究不同接收距离对采集信号的影响。
对应于裂纹起裂和稳态缓慢扩展两种情况,分别考虑梁中部下侧的点源开裂(初始裂纹形成)和梁中部受拉区已有裂缝(设0.05m)处产生新的单点开裂两种情况,分别对应于图3中的声源1和声源2。在声源一侧沿声源力激励方向(垂直于混凝土开裂方向)等距离选择3个点(其中声源1对应Pd1、Pd2、Pd33 点,声源 2 对应Pm1、Pm2、Pm33 点),距声源的距离分别为0.1,0.2,0.3m,采集其垂直于底面的速度响应信号(νy)。尽管在实际应用中难以用传感器采集梁中部这些点的y方向的速度响应信号,但了解其理论上的规律有助于探讨实际应用中上下表面采集信号的形成规律。

图3 不同接收距离的信号采集(分边界声源和内部声源两种情况)

图4 声源1产生的不同接收点的AE信号及其最大幅值随传播距离衰减规律
所得 3 点信号分别如图 4(a)和图 5(a)所示,其波形很好地反映了信号的传播特征。由于采集的是垂直于下表面的速度信号,由波的传播特性可知,首先到达的纵波,其幅值较小,但往往超过AE系统采集门槛而激发信号采集,并成为信号首波(图中时间0点处波形)。接着是横波和紧随其后的表面波,表面波表现为图中最大幅值,而横波因与之紧邻且幅值较小而不甚明显。随着传播距离的增加,波形整体呈衰减趋势。为更好地表现信号幅值随传播距离变化的规律,图4(b)和图5(b)分别给出了两种情况下距声源0.3m范围内10个点的信号幅值。由图可见,由于面波在近场有一定的形成机制,信号的变化规律较为复杂,分别从0.18,0.12 m向外起,信号的衰减才遵循指数衰减规律。
2)不同接收方位对声发射信号的影响

图5 声源2产生的不同接收点的AE信号及其最大幅值随传播距离衰减规律

图6 不同方位的接收点及上表面接收点
传感器位置对采集信号的影响除传感器与声源的距离外,还与方位有关。接收方位以声源和接收点的连线与开裂方向之间的夹角表示。对接收距离为0.1m,夹角分别为 0°、30°、45°、60°、90°及 120°6 点的AE信号进行了比较。其中,0°点位于裂缝扩展前方,90°点为点源力作用方向,而120°点正好位于梁的下表面(见图6)。
由图7所示各点AE波形可见,由于内力源的方向垂直于开裂方向,在0°~90°角之间信号幅值总体随着角度的增加而增大,但除0°角和120°角外差别并不显著,且具有相似的波形。而0°角接收点位于裂缝前方,因而信号波幅很小;120°点则正好位于梁的下表面,除接收到纵波和横波外,还有幅值更大的表面波。

图7 不同方向接收点的AE信号
可见,在布置传感器时应注意不宜将传感器安装在可能的开裂前方位置(0°角附近),而选择30°~90°角之间的点较为合适。从采集的信号来看,垂直于裂缝的90°角方向信号受到的干扰最小,但实际情况下往往难以实现此方向的安装。因此综合上述信号特点,将传感器安装在45°方向的表面上比较好。
120°点的接收信号以幅值较大表面波为主。表面波由声源信号沿裂缝表面下行至下表面后再沿下表面传播形成,因而造成信号波形相对复杂。此外,若传感器置于构件开裂侧,则开裂位置可能恰好发生于传感器粘接处,造成信号剧烈变化。但传感器置于下表面(开裂面)也有一定的优势:由于表面波能量损失较小,传播距离远,因此在大型结构的AE检测中,可利用该特点将传感器布于构件的开裂侧,并保持较大的传感器间距,从而节省传感器数量。但需注意此时对声源的定性和定量判断准则与他处有较大差异。

图8 梁上表面不同接收点的AE信号及其最大幅值随传播距离衰减规律
对图6中梁上表面等间距的3点Pu1、Pu2、Pu3来说,既有接收距离的差别,又有方位角的差别。但由于处于上表面,该3点均处于合理的方位角范围内(37°~67°),因此,信号幅值的差别主要来自距离的影响。即除靠近对称轴附近由于方位角很小(0°附近)使得幅值较小外,总体是距离越远,幅值越小的规律(图8(a))。同时可见,随着传播距离的增加,横波与纵波的到达时间也相应增加,使得图中两者的时间差也越来越远。因此,由信号中横波与纵波间的时间差亦可判断声源距离,并作为声源定位的依据。图8(b)反映了上表面各接收点AE信号幅值随传播距离衰减的规律,其中靠近对称轴区域的接收点由于方位角较小,AE信号幅值较小,且距离(角度)稍有增加信号幅值即迅速增大。该区域实际上属于“圣维南区域”,信号变化较为剧烈,不适合用于声源定量分析,因此布置传感器时应尽量避开,但离开的距离太远时又会使信号有较大衰减。因此,与前述结论相同,实际应用中应将采集点设置在距对称轴(开裂线)的距离与梁高相当的位置,使其处于合理的方位角范围内,并获得清晰信号。
根据上述不同传感器接收位置处声发射信号的讨论,可得AE信号的变化规律如表1所示。由此可总结出传感器安装准则如下:
1)对高度较小的梁可置于开裂侧对面的表面上,水平距离为一倍梁高附近,使方位角和距离均处于较佳的范围,以获得更好的波形。
2)对较大的梁,可置于开裂侧表面,以获得较大的信号。
实际AE测试中,开裂位置往往无法事先确定,则可根据传感器阵列进行定位,并根据定位结果,结合该准则确定传感器阵列中的最佳传感器位置,并以该传感器信号进行损伤识别。
3.2 不同开裂程度对声发射信号的影响
对实际混凝土构件而言,开裂程度包含多层含义。如裂缝已经扩展的程度(构件所处的损伤状态)、单次开裂中裂纹扩展的长度(损伤状态的变化程度)、裂纹扩展的速度(损伤状态的变化速度)等。在AE测试期间,安装好的传感器通常不再更改位置。因此研究不同开裂程度对AE信号的影响旨在了解AE信号特性是否有较大变化,以便于损伤识别时采取相应的应对措施。
首先考虑不同开裂位置(损伤状态)的影响,即在已开裂的不同程度下,由裂尖处新的点源模拟微裂纹引起的AE信号(图9);其次针对不同的开裂长度(损伤变化程度),以点源模拟微裂纹的形成,较短的线源模拟规模较小的裂纹扩展,较长的线源对应严重的稳定扩展或失稳扩展;最后考虑开裂速度,较低的速度对应较稳定的扩展,较高的速度对应较严重的扩展。

表1 不同位置AE传感器接收信号规律
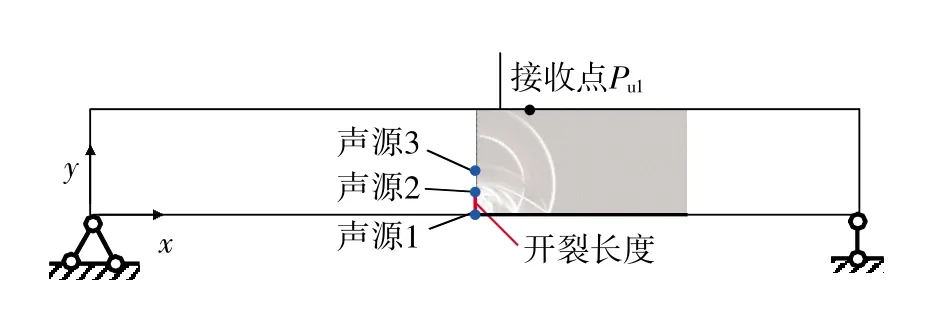
图9 不同开裂程度下的声源及接收点

图10 不同开裂程度的AE信号
根据表1的规律,选择梁上表面距声源水平位置0.1 m的点Pu1作为信号接收点(图9),以便对不同开裂程度下的AE波形进行比较。
图10(a)为3个不同位置(相距0.05 m)点源激发,同一点(Pu1点)接收的AE信号。由于均为点源激励,故总体而言三者具有相似的波形特征,纵波和横波清晰可见,而后续的边界反射波也隐约可见。只是相对而言,后两个位置均处于已有裂缝尖端,声源发射时有部分波沿裂缝面下行,使得上表面接收点的波形幅值变小,继而下行波再次反射向上将形成干扰波,使得波形中的反射波更加复杂。
其次是开裂长度的影响。分别对点源、开裂长度为0.05m、开裂长度为0.1m 3种情况进行了计算和分析。混凝土材料中裂纹的扩展速度通常在1500m/s以下[13],小于波的传播速度,因此计算中开裂速度均假设为1000m/s。对于线源,可通过在加载区按时间顺序施加若干偶极子实现,且相邻加载时间的延迟取决于开裂速度。
图10(b)为上述3种情况下Pu1点采集的信号。线源产生的AE信号实际上反映了更为严重的损伤事件,因此必须对其特征进行了解。由于线源开裂为一系列连续的声源,先后发出的AE波相互叠加形成最终波形,其波形特性与波速、开裂速度及构件尺寸等均有关。总体而言信号能量随开裂长度增加而增大(但并非比例关系),信号持续时间也随之增加,波形相对较为复杂。
最后研究开裂速度的影响。在同样开裂长度下(0.05m),分别以 500,750,1000,1250,1500,1750m/s的开裂速度进行比较。结果表明,各信号具有显著不同的时域和频域特征(频域分析由基于Hilbert-Huang变换的边际谱分析得到),且无明显规律。这是由于线源开裂信号来自连续的多源激励及复杂的边界反射的波形叠加,其叠加结果受各波形的相位特征影响很大,使得合成信号的幅值和频率特征具有较大的离散性。况且材料的开裂速度往往难以确定,因此实际检测中以开裂速度衡量开裂状况并探寻其AE特性并不可取。可采用同样反映开裂破坏程度,并与开裂速度密切相关的开裂长度作为衡量指标。
综上所述,当构件发生显著开裂破坏时(线源),声发射信号具有幅度大、能量大、持续时间长、波形复杂等特点,其幅值超过点源信号1~2个数量级(图10(b))。在此情况下,传感器位置对信号波幅的影响可以忽视。
4 结束语
本文通过对混凝土构件中常见开裂形式的数值模拟,分析了AE信号的变化规律,提出AE检测中传感器的安装准则,主要结论如下:
1)通过不同接收位置信号的波形分析,总结了用于AE检测的传感器安装准则,为获取清晰、稳定、不失真的AE信号提供理论依据。
2)当构件发生显著裂纹扩展破坏时,传感器位置对信号波幅的影响通常可以忽视,但仍需避开不合理安装区域。
3)由于计算的复杂性,数值模拟基于简化的均质材料,而实际钢筋混凝土结构中钢筋的对波影响不容忽视,需进一步研究以使结论更具广泛意义。
[1]ROBINSON S R.Methods of detecting the formation and propagation of microcracks in concrete[C]∥Proceeding of the Internet Conference of Structure of Concrete.London: Cement and Concrete Association, 1965.
[2]GREEN A T.Stress wave emission and fracture of prestressed concrete reactor vessel materials[C]∥Proc 2nd Interamerican Confon MaterialsTechnology.ASME,1970.
[3]MCCABE W M,KOERNER R M,LORD A E.Acoustic emission behavior of concrete laboratory specimens[J].Journal of the American Concrete Institute,1976,73(7):367-371.
[4]纪洪广.混凝土材料声发射性能研究与应用[M].北京:煤炭工业出版社,2004:34-53.
[5]杨明纬.声发射检测[M].北京:机械工业出版社,2005:18.
[6]杨占才,张来斌,刘玉辉,等.发动机活塞——缸套磨损过程声发射机理研究[J].石油矿场机械,2001,30(4):1-3.
[7]KAO D, GRAHAM D, KNIGHT B, et al.A mathematicaldescription ofthe acoustic coupling ofthe mass/spring model[J].Applied Mathematical Modelling,2007,31(12):2684-2695.
[8]SAUSE M G R,HORN S.Simulation of acoustic emission in planar carbon fiber reinforced plastic specimens[J].Journal of Nondestructive Evaluation,2010,29(2):123-142.
[9]OHTSU M.Source mechanisms of AE[M]∥GROSSE C U, OHTSU M.Acoustic Emission Testing.Springer,2008:149-174.
[10]OHTSU M.Source mechanism and waveform analysis of acoustic emission in concrete[J].Journal of Acoustic E-mission,1982(1):103-112.
[11]HORA P, CˇERVEN O.Acoustic emission source modeling[J].Applied and Computational Mechanics,2010(4):25-36.
[12]ONO K,CHO H,MATSUO T.Transfer functions of acoustic emission sensors[J].Journal of Acoustic E-mission,2008(26):72-90.
[13]赵向军,肖川.爆炸冲击载荷作用下钢筋混凝土介质裂纹扩展速度的实验研究[J].火炸药学报,2013(1):55-58,81.
(编辑:李妮)
Acoustic emission sensor installation strategy based on numerical simulation and waveform analysis
GU Aijun1,HAN Wenqin2
(1.School of Hydraulic,Energy and Power Engineering,Yangzhou University,Yangzhou 225127,China;2.School of Material Engineering,Jiangsu University of Technology,Changzhou 213001,China)
In order to improve the quality of acoustic emission signal acquisition and realize the reliable damage detection, a concrete component was studied numerically to investigate the quantitative relationship between cracking damage and acoustic emission signals.The propagation characteristics of signals were acquired by analyzing waveform of signals.The sensor installation guidelines, including avoiding Saint-Venant's area, eluding unreasonable orientation, and closing to the damage source,were established in accordance with the signal principle of clearness and stableness.Meanwhile it was confirmed that the influence of sensor position could be ignored when cracking was acute.The study provides a theoretical basis for sensors location and damage diagnosis by acoustic emission signals in practical engineering.
acoustic emission;numerical simulation;sensor installation strategy; waveform analysis;signal characteristics
A
1674-5124(2017)11-0117-07
10.11857/j.issn.1674-5124.2017.11.023
2017-04-09;
2017-05-13
住房和城乡建设部项目(2016-K4-074)
顾爱军(1968-),男,江苏泰兴市人,副教授,博士,主要从事固体力学与无损检测方法研究。

