基于局部均值分解的行波故障测距方法

刘伟鑫，周松斌，刘忆森，韩 威，张宏钊

（1.广东省智能制造研究所广东省现代控制与光机电技术公共实验室，广东 广州 510070；2.广东省智能制造研究所广东省现代控制技术重点实验室，广东 广州 510070；3.广东工业大学自动化学院，广东 广州 510006）

基于局部均值分解的行波故障测距方法

刘伟鑫1，周松斌2，刘忆森1，韩 威1，张宏钊3

（1.广东省智能制造研究所广东省现代控制与光机电技术公共实验室，广东 广州 510070；2.广东省智能制造研究所广东省现代控制技术重点实验室，广东 广州 510070；3.广东工业大学自动化学院，广东 广州 510006）

针对当前输电线路行波故障测距存在波速不确定性与行波波头到达时间难以准确测量问题，提出一种基于局部均值分解（local mean decomposition，LMD）的行波故障测距方法，该方法在传统双端测距线路中间增加一个测量点，利用无故障线段的长度和测量点检测波头时间求出输电线路的行波波速，有效消除波速对测距精度的影响；利用LMD算法对行波故障电流线模分量进行分解，根据分解得到第一个分量PF瞬时频率曲线的首个频率突变点准确测量行波波头到达时间。采用Simulink搭建输电线路仿真模型，将该文行波故障测距方法与小波变换测距、HHT变换测距方法（Hilbert-Huang transform，HHT）进行仿真对比，结果表明：该文方法测距精度高于小波变换测距、HHT变换测距方法，对实际输电线路故障测距具有重要应用价值。

行波故障测距；局部均值分解；输电线路；测距精度

0 引 言

随着现代电网发展以及供电质量不断提高，输电线路故障快速、准确定位已显得非常重要。其中利用电力输电线路在故障时产生的高频电磁波的特征进行故障定位的技术（即行波故障测距技术）由于具有高效、快捷的特点，已经成为主流的输电线路故障定位技术[1]，但目前还存在输电线路行波波速的不确定性、行波波头到达时间无法准确测量的问题。

目前国内外行波波速测量方法主要有人工设定法、区外故障测量法、在线测量法等。人工设定法根据实际经验将行波波速设定为固定值，在0.936 c（11kV）～0.987c（500kV）之间，线模分量行波波速通常为（2.95×105～2.96×105）km/s，但易受环境气候、地理位置等因素影响[2]；区外故障测量法根据输电线路区外故障时线路两端测量的行波波头时间之差结合线路参数计算出行波波速，但故障行波经母线折反射后会干扰测量；在线测量法是根据故障线路的折反射行波波头到达时间差来确定行波波速[3]，但会存在行波经多次折反射后衰减到难以测量。有学者提出相关波速修正模型减少波速误差，但获得准确波速修正模型比较复杂[4-6]。

目前国内学者主要采用的行波波头检测方法是小波变换（wavelet transform，WT），小波变换具有时-频局部化特性，能够有效分析信号奇异性，但是小波分析检测波头需结合行波信号特征来选择合适的小波基函数、分解尺度[7-8]；国外有部分学者采用希尔伯特-黄变换（Hilbert-Huang transform，HHT）检测行波波头，HHT变换方法克服小波基选取困难不足，是一种自适应信号分解方法，但其存在负频率、严重端点效应问题，影响波头检测准确度[9-11]。鉴于基于局部均值分解（local mean decomposition，LMD）算法[12]自适应时频分析方法可以将复杂非平稳信号分解为若干个PF分量，这些PF分量含有丰富的频率、包络信息，能够真实完整地反映原始信号的特征，近年来不少研究学者采用LMD算法[13-15]成功应用于旋转机械、机械部件等故障特征提取与诊断分析中，若能将其应用于电力行波暂态信号特征提取将是非常有意义探索工作。

本文提出一种基于局部均值分解行波故障测距方法，该方法能消除波速对测距精度影响，行波波头到达时间测量准确性较高。

1 消除波速影响行波故障测距方法

图1为本文提出可有效消除波速对测距精度影响的输电线路故障行波故障测距方法示意图。假设线路总长度为l，测量点M、测量点N分别装在输电线路的两端，测量点P装在输电线路两端中间，距离测量点M、测量点N分别为l1、l2，3个测量装置点采用LEA-6系列的GPS模块实现时间同步，时间同步精度可达30ns，满足输电线路行波故障测距精度要求。F点发生故障后，故障行波电流会往输电线路两端传播，传播速度为ν，测量点M、N、P分别测得行波波头到达的绝对时间 tm、tn、tp。由 l2除以 tn、tp的时间差可以求得行波波速，设故障点F到测量点M、N的距离为lMF、lNF，结合双端测距原理可得：

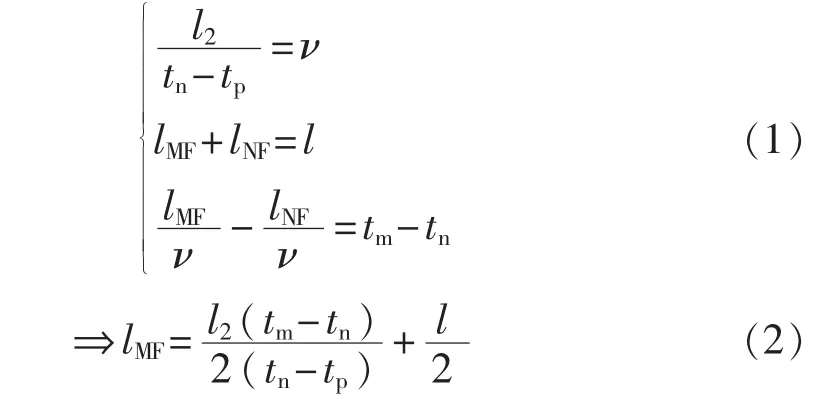
可以看出，该行波故障测距方法与传播速度ν无关，仅与测量3个测量点故障行波波头到达时间有关。

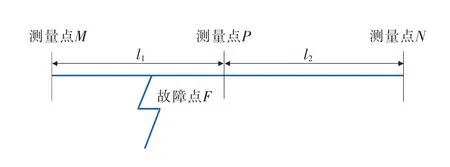
图1 输电线路故障行波3点测距示意图

图2 三相电路单相接地故障电流波形

2 基于LMD行波波头到达时间测量原理

输电线路故障暂态信号具有高频、瞬间突变的特点，输电线路故障发生时其电流、电压故障信号是非平稳信号，而LMD算法能将原始非平稳的复杂信号由高频往低频信号逐级分解，依次得到PF1、PF2等分量，故可采用LMD算法对输电线路发生的故障电流行波的线模分量进行分解，得到包含故障高频分量PF1，求取其瞬时频率曲线，借助瞬时频率曲线图上首个频率突变点可确定行波波头到达时间。

图2为三相输电线路单相接地故障某测量点测得三相故障电流情况，A相接地故障发生在第10000个采样点处，图中A相故障电流在第10000个采样点处发生激烈突变。

对三相输电线路由电流正常态到电流故障态过程看作一个非平稳信号，采用LMD算法检测故障行波波头到达时间。具体步骤：

1）由于三相电流信号存在耦合，需对三相故障电流进行凯伦贝尔变换进行相模变换解耦得到α模电流 Iα，如图 3（a）所示。Iα与 A、B、C 相电流 Ia、Ib、Ic以及为0模分量I0的关系为

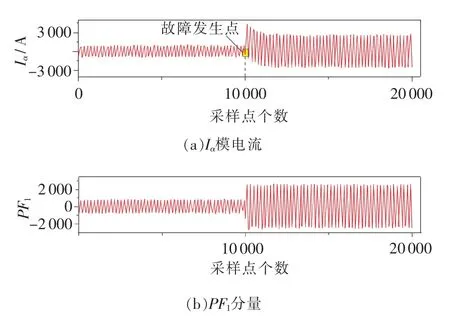
图3 Iα模电流及PF1分量

2）将 Iα（t）作为原始信号，求取局域均值函数mi、局域包络函数 ai：

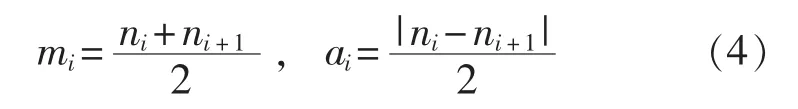
其中ni为原始信号Iα（t）极值点，然后采用移动平均法对 mi、ai进行平滑得到 m11（t）、a11（t）。

3）用式（5）将 m11（t）从信号 Iα（t）分离得 h11（t），用式（6）对 h11（t）进行解调得 s11（t）：

4）理想情况下 s11（t）是一个纯调频信号，可满足-1≤s11（t）≤1。若 s11（t）不能满足，则将 s11（t）作为原信号重复2）～3）迭代过程，直到满足条件，得到纯调频信号 s1n（t），即包络估计函数 a1（n+1）（t），即：

实验中 a1（n+1）（t）很难满足，可能会导致分解过程发散。实际应用中，可设定一个小变化量ε，满足1-ε≤a1n（t）≤1+ε 时，迭代终止。经测试，若取 ε=0.001时，可使Iα（t）有较高分解精度又不致迭代死循环。

5）将以上迭代过程中求得的局域包络函数相乘之积与纯调频信号 s1n（t）相乘，便可得到原信号 Iα（t）的第一个 PF 分量（见图 3（b））。

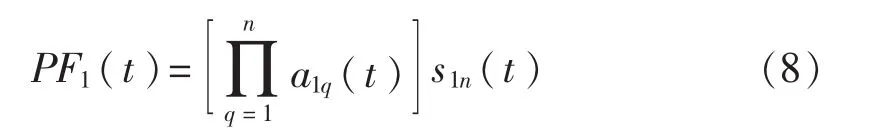
6）LMD 分解从高频往低频，PF1（t）包含原信号中最高频率成分，包含电流高频故障信号，可求得其瞬时频率 f1（t）：

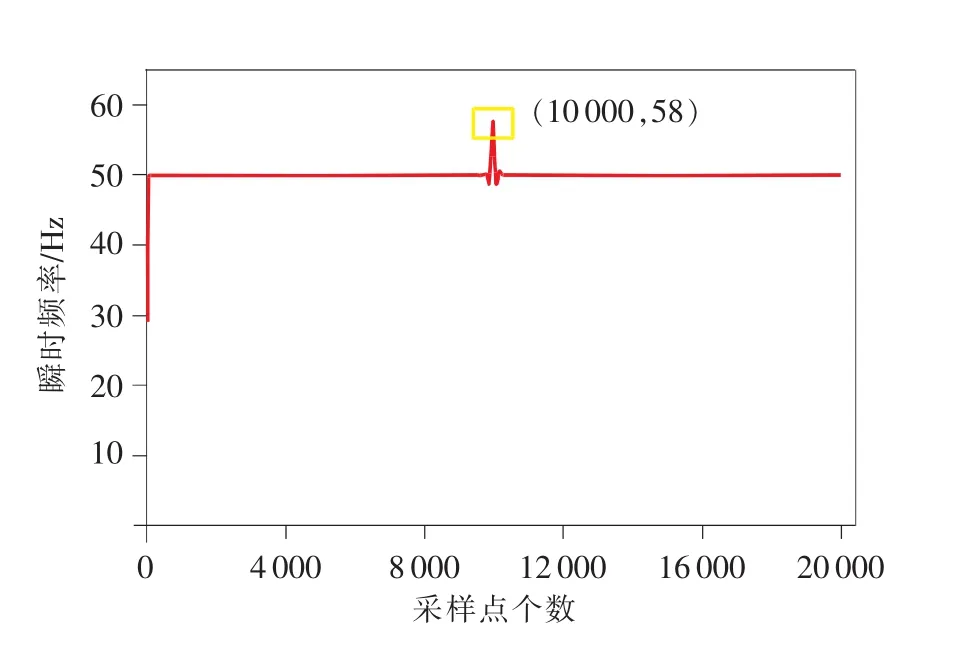
图4 PF1瞬时频率

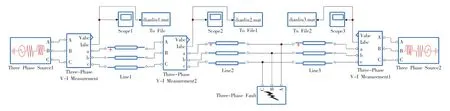
图5 输电线路仿真模型

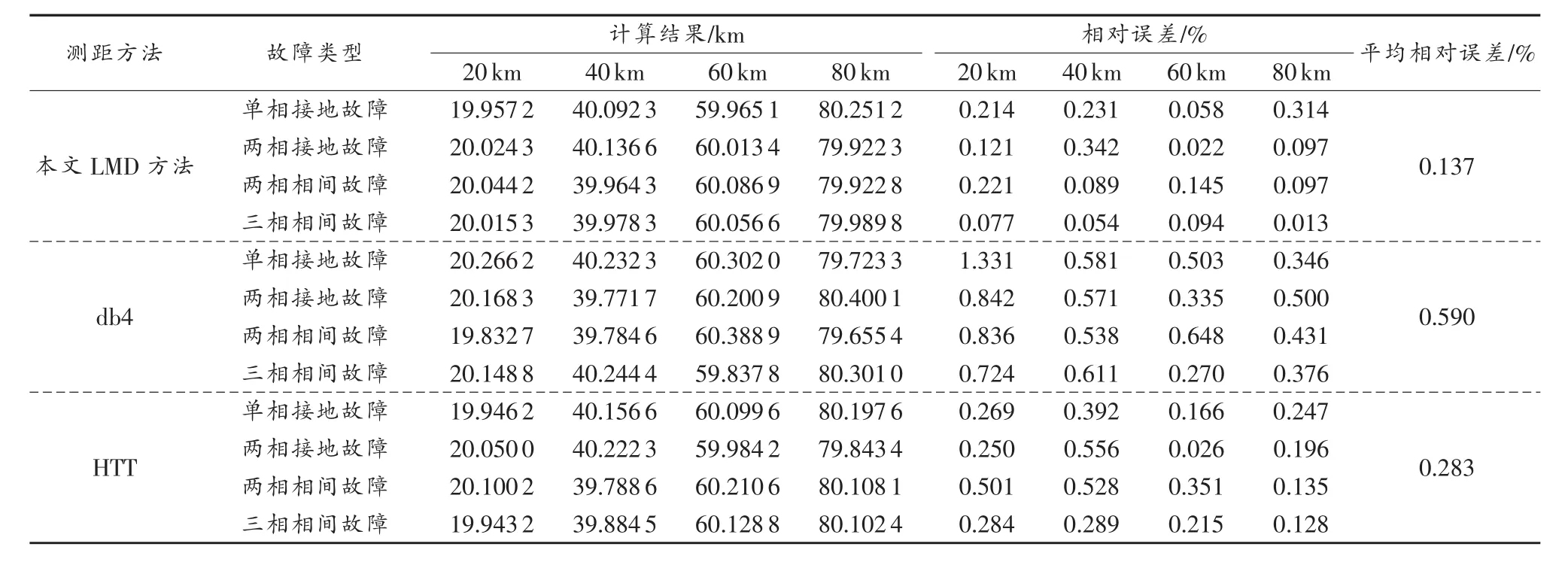
表1 LMD、db4小波变换、HHT变换在各类故障下不同故障距离计算测距结果对比分析

求得 PF1（t）瞬时频率（见图 4）。

输电线路在正常情况下电流频率50Hz，若在某个采样点时刻发生单相接地故障，则该点电流发生突变，图4中反映在第10000个采样点处瞬时频率曲线急剧上升，很好地检测到故障行波波头到达时间，故可通过判断LMD分解故障电流行波线模电流的PF1分量的瞬时频率曲线的首个频率突变点,确定行波波头到达时间。

3 实验仿真

3.1 仿真模型搭建

图5为采用Matlab/Simulink PSB工具箱搭建输电线路行波故障测距仿真模型（参数设置500 kV三相恒压电源、分布式参数的输电线路模型、输电线路总长l=100km）。利用工具箱的三相故障发生器，可模拟单相接地短路故障、两相接地故障、两相相间短路故障和三相短路故障，故障点分别设在距M端距离 L1=20，40，60，80km 处，0.002s时刻发生故障，测量装置分别安装于线路两端、中间位置，采样频率设置为10kHz。输电线路各参数：频率f=50Hz，正序参数电阻 R1=0.0212Ω/km、电感 L1=0.897×10-3H/km、电容C1=12.9×10-9F/km；零序参数电阻R0=0.1142Ω/km，电感 L0=2.2886×10-3H/km，电容 C0=5.2×10-9F/km。

3.2 仿真结果分析

为更好了解基于LMD的行波故障测距方法的测距效果，采用上述输电线路模型在相同的实验条件下对基于LMD的行波故障测距、db4小波变换测距、HHT变换测距方法进行仿真对比分析，实验数据如表1所示，基于LMD的行波故障测距方法在单相接地短路故障、两相接地故障、两相相间短路故障和三相短路故障类型下不同故障距离的测距误差较小，经计算平均相对误差仅为0.137%，db4小波变换测距方法为0.590%，HTT变换测距为0.283%，可见基于LMD的行波故障测距方法相比db4小波变换测距、HTT变换测距在各种故障类型、不同故障距离，具有更高的测距精度。3种测距方法的差别在于行波波头到达时间的测量精度，小波变换行波波头到达时间测量精度取决于选择合适的小波基和分解层数，但选择合适的小波基和分解层数并不容易，需要进行多次实验测试，且不具有自适应性，会影响到测量行波波头到达时间的测量精度；HHT变换行波波头到达时间测量方法克服小波变换的缺点，具有自适应性，但其存在过包络、欠包络、严重端点效应、负频率等问题会一定程度上影响到行波波头到达时间的测量精度。

4 结束语

1）针对输电线路行波波速难以准确测量的问题，本文提出一种行波故障测距方法，在传统双端测距线路中间增加一个测量点，利用无故障线段的长度和测量点检测波头时间求出输电线路的行波波速，有效消除波速对测距精度的影响，对实际行波故障测距有一定参考价值。

2）针对行波波头到达时间检测常用的小波变换方法存在小波基和分解尺度选择困难以及HHT变换方法存在过包络、欠包络、负频率、端点效应严重等问题，本文采用局部均值分解算法分解故障电流线模分量，得到高频分量PF1，对PF1分量求取瞬时频率并查找首个频率突变点准确测量行波波头到达时间。

3）通过Matlab/Simulink搭建输电线路仿真模型并结合Matlab编程对本文提出的基于局部均值分解的行波故障测距方法以及小波变换测距、HHT变换测距方法在不同故障类型、不同故障距离进行仿真对比分析，仿真表明基于LMD的行波故障测距方法相比db4小波变换测距、HHT变换测距方法具有更高的行波故障测距精度。

文献参考

[1]覃剑，陈祥训，雷林绪.输电线路行波故障测距技术与小波变换应用[M].北京：中国电力出版社，2014：5-6.

[2]申文，刘亚东，盛戈皞，等.输电线路实际运行状态对行波波速的影响 [J].电力系统及其自动化学报，2014（9）：12-16，29.

[3]位韶康，陈平，姜映辉.一种不受波速影响的单端行波测距方法[J].电力系统保护与控制，2013（13）：76-81.

[4]唐金锐，尹项根，张哲，等.零模检测波速度的迭代提取及其在配电网单相接地故障定位中的应用[J].电工技术学报，2013（4）：202-211.

[5]徐敏，蔡泽祥，刘永浩，等.基于宽频信息的高压直流输电线路行波故障测距方法 [J].电工技术学报，2013（1）：259-265.

[6]刘永浩，蔡泽祥，徐敏，等.基于波速优化与模量传输时间差的直流线路单端行波测距新算法[J].电力自动化设备，2012（10）：72-76.

[7]张广斌，束洪春，于继来.基于Hough变换直线检测的行波波头标定[J].中国电机工程学报，2013（19）：165-173，176.

[8]WANG Y， ZENGX J， QINX A， et al.HHT based single terminal traveling wave fault location for lines combined with overhead-lines and cables[C]∥Power System Technology（POWERCON），2010 International Conference on Hangzhou，2010：1-6.

[9]范新桥，朱永利.基于双端行波原理的多端输电线路故障定位新方法[J].电网技术，2013（1）：261-269.

[10]HAN F L， ZHAO X， ZHANG Y， et al.Research on single-phase-to-earth fault location based on Hilberthuang transform[C]∥2016 IEEE Advanced Information Management， Communicates，Electronic and Automation Control Conference （IMCEC），Xi’an，2016：1338-1341.

[11]WANG D， GAO H L， LUO S B， et al.Travelling wave fault location principle based on Rogowski coil's differential output and Hilbert-Huang transform[C]∥13th International Conference on Development in Power System Protection 2016（DPSP），Edinburgh，2016：1-6.

[12]SMITH J S.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface，2005，2（5）：443-454.

[13]孟宗，王亚超.基于微分局部均值分解的旋转机械故障诊断方法[J].机械工程学报，2014（11）：101-107.

[14]XU T， YIN Z， CAI D， et al.Fault diagnosis for rotating machinery based on local mean decomposition morphology filtering and least square support vector machine[J].Sojournal of Intelligent and Fuzzy System，2017：2061-2070.

[15]张淑清，孙国秀，李亮，等.基于LMD近似熵和FCM聚类的机械故障诊断研究[J].仪器仪表学报，2013（3）：714.

（编辑：刘杨）

Traveling wave fault location measurement method based on LMD

LIU Weixin1， ZHOU Songbin2， LIU Yisen1， HAN Wei1，ZHANG Hongzhao3
（1.Public Laboratory of Modern Control and Optics-Mechanics-Electricity Technology，Guangdong Institute of Intelligent Manufacturing，Guangzhou 510070，China；2.Key Laboratory of Modern Control Technology，Guangdong Institute of Intelligent Manufacturing，Guangzhou 510070，China；3.Faculty of Automation，Guangdong University of Technology，Guangzhou 510006，China）

In view of the problem of the wave velocity uncertainty and the inaccurate measurement of the arrival time of initial traveling wave in travelling wave fault location measurement of transmission line， a traveling wave fault location measurement method based on local mean decomposition （LMD） is proposed in this paper.It can eliminate the influence of wave velocity to fault location measurement by adding a measurement point in the middle of the traditional Double-Ended Traveling Wave and calculating the traveling wave velocity with the length of faultfree line segment and the time that the initial wave is tested at the measurement point.The local mean decomposition is applied to decompose the line mode component of measured current wave，and the arrival time of the initial traveling wave can be detected according to the first sudden arising of frequency in the instantaneous curve of the first PF obtained through LMD.The transmission line simulation model of the Simulink is established in the paper.The results of the simulation comparison conducted for LMD，Wavelet Transform and Hilbert-Huang Transform（HHT） show that LMD has higher fault location measurement accuracy than the schemes based on either wavelet transform or Hilbert-Huang transform and it has a certain reference value to transmission line fault location measurement in practice.

travelling wave fault location；LMD； transmission line； location accuracy

A

1674-5124（2017）09-0042-05

10.11857/j.issn.1674-5124.2017.09.008

2017-03-15；

2017-04-29

广东省科技计划资助项目（2015B090901025，2016B090918061）

刘伟鑫（1992-），男，广东揭阳市人，助理工程师，主要从事测控系统技术集成与应用。