基于PSO－BP神经网络的风电功率预测研究＊

鲁娅楠，王金梅，2，孙 帆

（1.宁夏大学物理与电子电气工程学院，宁夏银川750021 2.宁夏沙漠信息智能感知自治区重点实验室，宁夏银川750021）

1 引言

精确的风电功率预测可以提高风电场的工作效率和供电的可靠性，也可为电网调度部门提前安排电力电源开机方式及做好应急预案提供参考，以确保电网安全稳定运行。

BP神经网络是一种包括隐含层的多层前馈神经网络，主要特点是信号向上传递，误差向下传递，能较好地解决隐含层连接权值在多层网络中的学习问题，但训练收敛速度慢，易陷入局部最优，不利于全局寻优[2，3]。PSO算法源于对鸟群觅食行为的研究，是模拟这种生物种群行为特征而提出的一种群体寻优算法，具有控制参数少、收敛速度快和全局寻优的优点，但它易陷入局部最小[4]。文献[5－8]提出用 PSO算法来优化BP神经网络的初始权值和阈值，这不仅可以避免BP网络局部寻优，还可以提高PSO算法的全局寻优能力、网络训练速度和预测精度。

因此，本文将PSO和BP算法也运用到风电功率预测中，结合BP神经网络局部寻优和PSO算法全局寻优的特点，用PSO算法优化BP神经网络的最初权值和阈值，然后不断更新粒子位置和速度，直到搜索出最优适应值，以提高网络训练速度和预测精度，将风电输出功率的不确定性变为可预测性。

2 风电出力特性分析

风的随机性、季节性和间歇性特点，使得风电出力的波动性较大。图1为某风电场春、夏、秋、冬四个季节普通日风电平均出力曲线图，图2为春、夏、秋、冬四个季节典型日风电实际出力曲线图。对比图1和图2不难发现，普通日的风电出力变化显示出比较明显的峰谷特性，出力的变化率相差较大；典型日风电平均出力峰谷差别不明显，出力比较稳定，变化率相差不大。

图1 风电场春、夏、秋、冬普通日风电平均出力曲线

图2 风电场春、夏、秋、冬典型日风电实际出力曲线

季节不同风电出力也不同，图1和图2都显示出冬季的风电出力相对较多。普通日冬季风电出力的峰谷差约为25000MW；典型日冬季风电出力的峰谷差约为3000MW；普通日出力较低的是夏季峰谷差约为35000MW；典型日出力较低的是秋季峰谷差约为5500MW。因此，分析普通日风电出力的特点，找到其变化规律，使研究更具普遍性。

3 PSO－BP网络算法流程

PSO－BP算法是将BP神经网络局部寻优和PSO算法全局寻优的优点结合起来，利用PSO算法优化BP网络的权值和阈值，然后不断更新粒子位置和速度，直到搜索出最优适应值，以提高网络训练速度和预测精度。PSO－BP模型算法步骤如下：

步骤1：确定BP神经网络结构，即输入层、隐含层、输出层神经元n、l、m的个数。

步骤2：初始化BP神经网络（权值、阈值）以及粒子群（粒子的位置、速度等）。

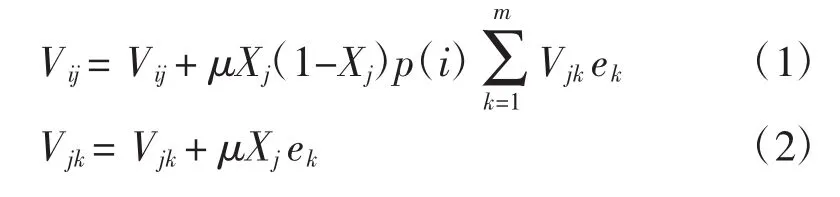
其中，i＝1，2，…，n；j＝1，2，…，l；k＝1，2，…，m；Vij、Vjk为 BP 神经网络的连接权值；Pi、Xj分别为输入层输入和隐含层输出；μ为学习速率；ek为误差。

其中，j＝1，2，…，l；k＝1，2，…，m；aj、bk分别为隐含层和输出层的阈值。

步骤3：计算粒子的适应度值F。

步骤4：搜索粒子个体极值Gbest和群体极值Zbest。如果目前适应度值优于Gbest，则更新粒子的Gbest，如若不是则更新粒子的速度和位置。如果全部粒子当前的适应值优于Zbest，则更新Zbest。

步骤5：根据式（6）和式（7）更新粒子的速度V和位置X。

其中，c1是粒子自身加速系数；c2是全局加速系数；μ1、μ2是分布在[0，1]区间的随机数；ρ是约束因子。

步骤6：根据式（8）更新权值ω。

其中，Tmax是迭代次数，ωmax、ωmin分别为最大和最小权重，t为当前迭代值。

步骤7：检查是否满足终止条件。若是则停止迭代，得到BP网络的最优权值和阈值，否则返回步骤3，重新计算粒子的适应度值。

步骤8：计算误差，然后更新权值和阈值，检查是否满足结束条件（当前位置或迭代次数是否达到预定误差）。若是则停止迭代，输出神经网络最优权值和阈值，否则重新计算误差。PSO－BP模型算法流程如图3所示。

图3 PSO－BP算法流程图

4 算例分析

4.1 样本处理

本文将所有样本抽出10%作为测试样本，其余部分作为训练样本，最后将测试样品的实际输出与预测输出进行对比。网络训练前先对所有样本数据进行归一化，即将样本数据处理在区间[0，1]，目的是提高预测模型的精度，加快网络的收敛性。用式（9）对样本数据进行归一化。

式中，Z＊为归一化后的输出数据；Z为原始输出数据；Zmax和Zmin分别为Z的最大值和最小值。

4.2 参数优化

BP神经网络结构的隐含层、输出层的传递函数分别为S函数‘tansig’和线性函数‘purelin’，训练次数为 200次，训练目标为 1e－5，学习速率为 0.02，权值为 4×5＋5×1＝25 个，阈值为 5＋1＝6 个。PSO 优化算法的参数如下：迭代次数为1000，最大速度为0.5，加速因子 c1＝c2＝2，ωmax＝0.9，ωmin＝0.3，设定最小误差为0.001，粒子数为40，粒子群个体维数为31。最后，用均方误差（RMSE）和平均相对误差（MAE）检验PSO－BP风电功率预测模型的精确度，公式如下：

其中，n为所有数据量，pi为风功率样本实际值，为预测值。

4.3 模型预测分析

图4 PSO适应度曲线

将训练好的样本数据输入PSO－BP网络预测模型，用Matlab工具进行仿真，模型输出的PSOBP神经网络的适应度曲线如图4所示，群体最佳适应度和当时的位置分别为1.1108e＋5和72，说明该模型有很好的收敛效果。PSO－BP风电功率实际值和预测值曲线如图5所示，其中蓝色实线代表的是风电输出功率的实际值，绿色虚线代表的是风电输出功率的预测值，从图中可以看出，预测值和实际值的变化趋势基本相同。

图5 风电功率实际值和预测值曲线图

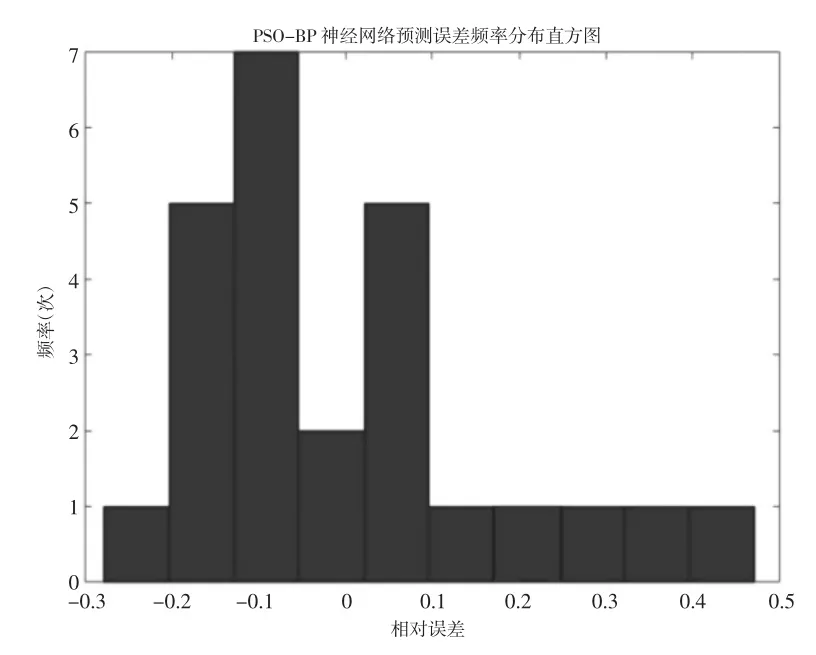
图6 均绝对误差频率分布直方图

图7 均方误差图

网络训练结束后，PSO－BP神经网络的误差频率直方图如图6所示，均方误差如图7所示。RMSE＝0.1548，MAE＝0.1164，MSE＝0.0048。从图 6 可以看出，PSO－BP神经网络预测误差基本呈正态分布，相对误差较小，从图7可以看出该网络的拟和能力较好。文献[12]基于IPSO－BP神经网络模型的风电功率预测研究中PSO算法的最佳适应度为17.21，PSO－BP算法的MAE为15.18%。对比发现，本文运用的基于PSO－BP神经网络的预测模型具有较好的预测精度和准确度。

5 结束语

针对大规模风电集中并网、远距离传输对电网安全稳定运行带来的影响，文章通过分析风电出力变化特点，用PSO－BP神经网络预测模型对未来几小时或者几天的风电功率进行预测，将风电输出功率的不确定性变为可预测性，并对该预测模型进行验证。结果表明，本文提出的PSO－BP预测模型训练速度快、预测精度高，可为今后电网的调度运行提供技术支持，可确保电网的安全稳定运行。