基于实测数据的鄱阳湖悬浮泥沙粒度遥感反演模式分析
, , ,,刚华
(江西理工大学 建筑与测绘工程学院,江西 赣州 341000)
基于实测数据的鄱阳湖悬浮泥沙粒度遥感反演模式分析
况润元,谢佳,张萌,李文红,张刚华
(江西理工大学 建筑与测绘工程学院,江西 赣州 341000)
水体悬浮泥沙粒度是重要的水质参数之一,影响着水体的遥感反射率。研究两者之间的关系对于内陆湖泊水环境遥感监测具有重要意义。基于鄱阳湖实测数据,采用相关分析方法,用不同数学模型进行鄱阳湖悬浮泥沙粒度反演研究。研究结果表明:①浑浊区适合采用体积百分比众数粒径建立反演模型,清水区适合采用数量百分比中值粒径建立反演模型;②浑浊区悬沙粒度的敏感单波段是环境卫星Ⅳ波段,在清水区悬沙粒度的敏感单波段有环境卫星Ⅱ和Ⅲ波段,而环境卫星Ⅱ,Ⅲ波段比组合是整个研究区水域的敏感波段;③单波段反演模型中,幂函数适用于鄱阳湖粒度遥感反演;波段比反演模型中,多项式模型适于鄱阳湖粒度遥感反演。
鄱阳湖;悬浮泥沙粒度;遥感反射率;定量反演;敏感波段
1 研究背景
水体悬浮泥沙是水环境监测的重要因素,悬浮泥沙的粒度大小及分布特征不仅体现了水体中颗粒物质的存在状态,而且悬浮泥沙粒度组成还可以指示水动力及再悬浮作用的过程和强度[1]。由于水体悬浮泥沙粒度大小影响水体的反射率,因此,含有不同悬浮泥沙粒度的水体具有不同的反射率曲线特征[2]。开展水体中悬浮泥沙粒度反演研究,有利于更好地理解和分析悬浮泥沙的光谱特征,对水体悬浮泥沙动态监测具有重要的意义。
常规的水体悬浮泥沙测量是用船舶逐点进行水样采集,然后在实验室进行分析,这耗费较大的人力、物力,调查速度慢、周期长,且只能获得在时间和空间上较少的离散的点位分布数据,虽实测的精度较高,但点位较为离散,难以满足大面积调查的要求[3]。传统的方法难以对悬浮泥沙的粒度特性进行持续的、动态的监测,而遥感以其成像范围广、周期短等优势能够快速地获取大面积水域内悬浮泥沙的信息,是一种有效的宏观监测的重要手段[4-6]。
最大限度准确地建立悬浮泥沙粒度与遥感反射率之间的关系是实现高精度悬浮泥沙粒度反演的关键。本研究所用鄱阳湖水体遥感反射数据是通过AvaField-1便携式高光谱地物波谱仪实测所得,并进行同步水体采样。采用美国贝克曼库尔特激光粒度分析仪LS100Q分别测得基于体积百分比、表面积百分比、数量百分比下的中值粒径、平均粒径、众数粒径等一系列粒度参数,以确定最优粒度分布模式下的悬浮泥沙粒度反演以及为反演结果精度验证提供支持,选出适宜于悬浮泥沙粒度反演的敏感波段和最优单波段及波段比组合,建立鄱阳湖悬浮泥沙粒度反演的最优模型,有利于推进鄱阳湖水体悬浮泥沙动态监测研究,并为鄱阳湖水域水色参数研究提供参考和理论依据。
2 研究区域及数据采集方法
2.1 研究区域
鄱阳湖位于115°49′E—116°46′E,28°24′N—29°26′N之间,地处江西省北部,长江中下游南岸,是我国第一大淡水湖,湖面面积约2 933 km2,集水约276亿m3,最大水深16 m[7]。鄱阳湖有70%的水域在江西省九江境内,20%的水域在江西省上饶境内,10%的水域在江西省南昌境内,汇集赣江、修水、饶河、信江、抚河5河之水,经九江市湖口县注入长江。鄱阳湖是一个南高北低,以吞吐流为主的高动态多泥沙的湖泊,湖区水中悬浮泥沙主要来源于流域水土流失及长江水倒灌、挖沙等[8-9]。鄱阳湖年均降雨量1 636 mm,每年4—6月份为最大降水期,11月份—次年4月份为枯水期。
2.2 水样采集与粒度测量
本研究野外水样采集在2013年10月份—2014年9月份丰水期分3次实施。第1次在2013年9月30日—10月3日期间,路线自赣江北支入主湖至长江,共采集50个点位水样,测量过程中水域水体由清澈到浑浊变化;第2次在2014年7月4日—7月8日期间,测量区域为主湖区的松门山附近水域、入江通道至长江,共35个点位,测量过程中水域水体也由清澈至浑浊变化;第3次在2014年8月30日—9月2日期间,测量区域为主湖区东部水域,共采集25个点位样品,该区域水体相对清澈。3次野外测量采集水样站点共计110个,测量站点分布如图1所示。

图1研究区站点分布
Fig.1Sitedistributioninthestudyarea
野外采集的水样在实验室采用激光粒度分析仪LS100Q进行悬浮泥沙粒度测量,测得基于体积百分比、表面积百分比、数量百分比下的中值粒径、平均粒径、众数粒径等一系列参数。将实验室测量采集的样品粒径数据除去未达到测量范围要求的20个站点数据,本研究将对所测得90个有效站点数据进行研究。其中,2013年9—10月份采样水域测得悬浮泥沙基于体积百分比的平均粒径介于1.76~6.885 μm之间,该区域基于体积百分比的中值粒径整体上高于平均粒径,3种分布模式下的粒径以体积百分比最高。2014年7月份采样水域采集的样品粒径大小在4 μm附近的比例最高,在星子县至主湖区范围内的粒径数据大小波动较小,分布较为密集;而在星子县至长江水域范围的粒径波动较大,分布较为离散。2014年8—9月份测量水域内所有采集样品的泥沙粒径整体偏小,3种模式下的粒径数据曲线变化趋势一致。
2.3 光谱数据采集
在野外采集水样的同时,同步采用AvaField-1便携式高光谱地物波谱仪对水体光谱数据进行测量,参考唐军武等[10]使用的水面以上反射率光谱数据的采集和处理方法,按照NASA测量规范使用光谱仪,测量得到所需的反射率光谱数据,推导出水体遥感反射率。野外使用光谱仪实测得到的数据主要为水面辐亮度Lsw(λ)、天空光辐亮度Lsky(λ)以及水面的太阳辐照度Ed(0+)。后期的数据处理中根据实测的光谱数据计算得到所需要的遥感反射率数据Rrs(λ),其公式为
(1)
式中:Lw(λ)为离水辐亮度;λ为波长;γ为气-水界面对天空光的反射率,与观测几何以及风速风向等因素有关。
同水样悬浮泥沙粒度测量保持一致,仅对90个有效站点光谱数据进行研究。为了更加准确地了解悬沙粒径和遥感光谱反射率之间的相关性,本研究在参考况润元等[11]根据悬浮泥沙浓度及遥感反射率对研究区的划分基础上将研究区分为浑浊区和清水区。所采集的站点数据中,浑浊区有72组数据,从中随机选取50组数据用于建立悬浮泥沙粒度与水体遥感反射率的反演模型,22组数据用于反演精度检验;清水区有18组数据,随机选取13组数据建立悬浮泥沙粒度与水体遥感反射率的反演模型,5组数据用于反演精度检验。根据野外实测数据,以体积百分比中值粒径为例,分别绘制不同粒度参数下浑浊区与清水区遥感反射率的变化曲线,如图2所示。

(a)浑浊区

(b)清水区
图2不同粒径反射光谱曲线
Fig.2Reflectancespectraofdifferentparticlesizes
本次实测光谱特征在不同水域以波长划分为不同特征段。浑浊区水域在350~560 nm波长范围内,遥感反射率随着波长的增加而不断升高,在560 nm附近出现第1个反射峰;在560~760 nm波长范围内,遥感反射率达到峰值后先随波长的增加而上下小范围波动,而后下降在740 nm附近出现反射谷;在760~900 nm波长范围内,遥感反射率先随波长增加而增大,在790~840 nm波段出现第2个反射峰,随后随波长增加而降低。清水区水域在350~560 nm波长范围内的反射率变化趋势同浑浊区一致,在560 nm附近出现第1个反射峰;在560~760 nm波段,反射峰与反射谷同时存在,670 nm附近出现第1个反射谷,690 nm附近出现第2个反射峰;700~740 nm波段反射率快速下降,750~800 nm波段反射率不变, 800 nm波段后反射率随波长增加而降低。
3 遥感特征因子与反演模型的选择
3.1 遥感特征因子选取
相对于海洋水体悬浮泥沙的研究,内陆湖泊水体对卫星遥感数据的空间分辨率要求更高。环境一号卫星CCD数据(简称HJ-1 CCD)具有高时相分辨率及宽覆盖的特征,在较短时间内能够完成全国范围的成像,周期为2 d,空间分辨率为30 m,幅宽700 km。因此,为便于后续使用HJ卫星影像数据,本文主要采用与环境卫星CCD(HJ-1 CCD)波段[12]对应的实测水体反射率数据,讨论鄱阳湖悬浮泥沙粒度遥感反演的最优模型。将其4个波段分别命名为Ⅰ波段(0.43~0.52 μm)、Ⅱ波段(0.52~0.60 μm)、Ⅲ波段(0.63~0.69 μm)、Ⅳ波段(0.76~0.90 μm)波段,相应的遥感反射率分别记为R1,R2,R3,R4。
确定敏感波段和选取最佳的遥感特征因子是建立反演模型的关键。遥感特征的选取,直接影响反演模型精度的高低,所以只有选择最佳的光谱特征因子,建立的模型精度才能达到最优,最后反演的结果才能达到最理想的状态。一些学者使用单波段遥感反射率,也有部分学者认为,不同波段反射比可以部分减少水表面光滑度随时间和空间变化的干扰,并在一定程度上减少其他因素的影响。因此,不同波段遥感反射率的比值常被用来建立悬浮泥沙的反演模型[13]。在此基础上,本文通过分析讨论,选取最优单一波段和最优波段比值作为遥感特征因子。
3.2 粒度遥感反演模型
悬浮泥沙浓度、悬浮泥沙颗粒大小等是影响水体悬浮泥沙遥感反射率的主要因素[14]。鉴于悬浮泥沙对水体反射光谱影响的复杂性,本研究结合野外实测数据,对几种常用数学模型进行对比分析,以确定在不同的水体悬浮泥沙浓度下,最适宜于建立遥感特征因子与悬浮泥沙粒度的反演模型。数学模型见表1。
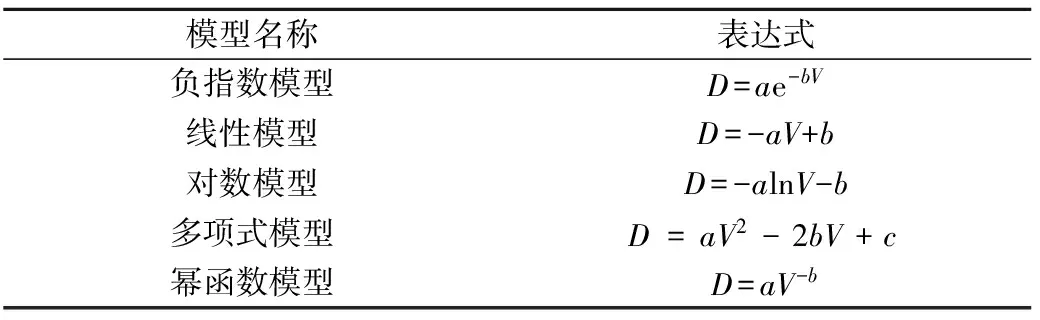
表1 悬浮泥沙粒度遥感反演模型
注:D表示悬浮泥沙粒度;V表示遥感特征因子;a,b,c均为待定参数
4 确定悬沙粒度参数及反演敏感波段
4.1 相关性分析
悬浮泥沙粒度与遥感光谱反射率之间的相关性是建立反演模型的基础,研究粒径参数与反射率之间的相关性是粒径反演的必要步骤[15]。对3次实测粒径数据与遥感反射率进行相关性分析,研究结果表明遥感反射率与一系列粒度参数相关性较差。沈芳等[16]通过试验研究认为,粒径与反射率的关系并不明显,但忽略了粒径变化对遥感反射率的影响可能导致较大的反演误差,粒径变化在遥感反演中应引起足够的关注。Bhargava等[17]认为在水体悬浮泥沙浓度一定时,悬浮泥沙粒径因子和水体的遥感反射率呈负相关。因此,为了选出相关性较好的波段和粒径参数,本研究在考虑悬浮泥沙浓度的前提下进行悬浮泥沙的粒度反演。
4.2 单波段和悬浮泥沙粒度的相关分析
浑浊区水域基于体积百分比、表面积百分比和数量百分比3种模式下的中值粒径、平均粒径以及众数粒径与遥感反射率的相关性如图3所示。其中,图3(a)、图3(b)、图3(c)分别是3种模式下相关系数与遥感反射率的相关分析图,图3(d)是3种模式下,相关系数与遥感反射率相关性最好的组合。基于体积百分比的众数粒径(以下简称体积众数)和基于表面积百分比的平均粒径(以下简称表面积平均)与遥感反射率的相关性较好。其中,350~420 nm波段,体积众数比表面积平均波动较大;450~560 nm及630~850 nm波段相关系数比较平稳;690~830 nm波段相关性最好,相关系数在-0.6左右。数量百分比各种粒径参数与反射率相关性较差。
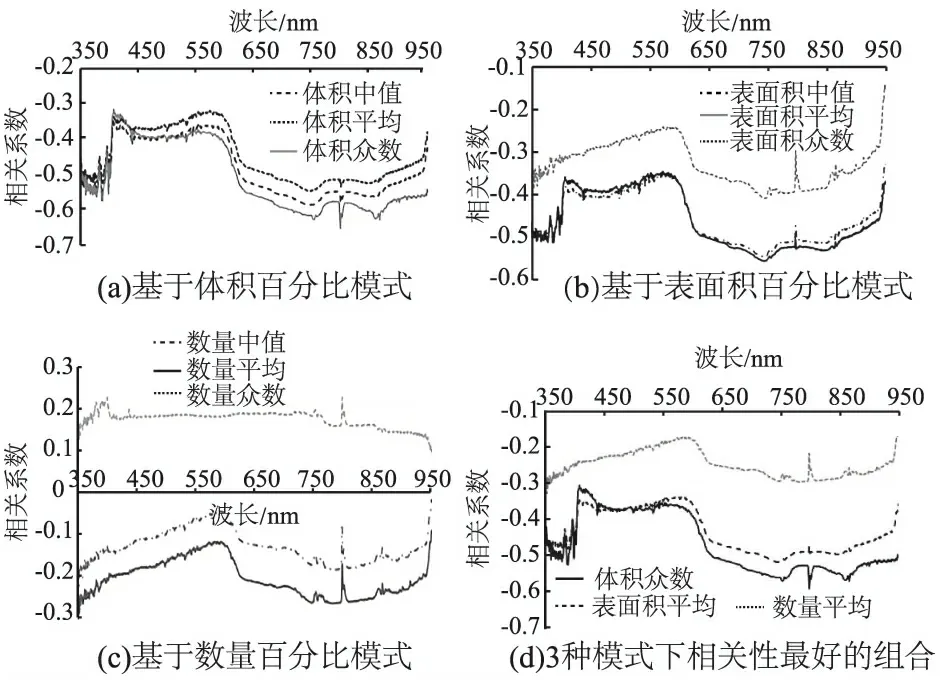
图3浑浊区粒度参数与反射率相关性
Fig.3Correlationbetweenparticlesizeandreflectanceinturbidarea
在低泥沙浓度的清水区,3种粒度分布模式下的中值粒径、平均粒径和众数粒径与反射率相关性如图4所示。其中,图4(a)、图4(b)、图4(c)分别是3种模式下相关系数与遥感反射率的相关分析图,图4(d)是3种模式下,相关系数与遥感反射率的相关性最好的组合。各参数与遥感反射率都为正相关关系,400~700 nm波段相关性最好,且无波动,曲线平稳,相关系数0.8左右,其中以数量百分比中值粒径(以下简称数量中值)相关性最优,故在清水区域使用数量中值作为反演参数因子建立模型。
根据分析结果,本研究在浑浊区以体积众数为参数、清水区以数量中值为参数分别与遥感影像各波段进行相关性分析,单波段相关系数如表2所示。

图4清水区粒度参数与反射率相关性
Fig.4Correlationbetweenparticlesizeandreflectanceinclearwater

表2 单波段与悬沙粒度的相关性
分析表2可知,在浑浊区,体积众数与Ⅳ波段的相关性最好,相关系数为-0.555 8;在清水区,数量中值与Ⅱ及Ⅲ波段的相关性较高,相关系数分别为0.910 2,0.922 3,相关性较高的波段可作为悬浮粒径反演敏感波段。
4.3 波段比和悬浮泥沙粒度相关性分析
将遥感影像4个波段反射率比值进行组合,计算波段比A1=R4/R3,A2=R4/R2,A3=R4/R1,A4=R3/R2,A5=R3/R1与浑浊区体积众数和清水区数量中值的相关系数,计算结果如表3所示。

表3 波段比与悬沙粒径的相关性
分析表3可知,浑浊区体积众数、清水区数量中值均与Ⅲ波段的反射比A4相关性最高,相关系数分别为-0.652 8,0.613 2,Ⅲ波段和Ⅱ波段的反射比可作为悬浮粒径反演敏感波段。
5 粒度反演及分析
5.1 浑浊区悬浮泥沙粒径反演
5.1.1 悬沙粒径与单波段反演
结合本研究4.2节相关性分析结果,以波段Ⅳ反射率R4为自变量,悬浮泥沙体积众数粒径Dr为因变量,构建悬沙粒度遥感反演模型,结果见表4。
表4浑浊区单波段悬沙粒度遥感反演模型
Table4Modelsofretrievingsuspendedsedimentparticlesizebysinglebandreflectanceinturbidarea

因变量自变量模型表达式决定系数y=5.0993e-18.79x0.3406y=-80.883x+5.37190.3189DrR4y=-1.141lnx-1.07570.3646y=3256.2x2-211.95x+6.10410.3850y=1.1441x-0.2640.3874
对表4中各种反演模型对比分析可知,幂函数的决定系数为0.387 4,高于其他模型的决定系数。将Ⅳ波段的粒度反演模型应用到22个检验点,实测众数粒径平均值4.713 2 μm,反演众数粒径平均值4.173 4 μm;最小绝对误差0.069 1 μm,最大绝对误差3.423 2 μm,平均绝对误差1.181 0 μm。
5.1.2 悬沙粒径与波段比反演模型
以Ⅱ波段、Ⅲ波段反射率比值A4为自变量,体积众数粒径Dr为因变量构建多种悬沙粒度遥感反演模型,结果如表5所示。可知其中以幂函数相关性最好。

表5 浑浊区Ⅱ,Ⅲ波段比反演模型
对比反演结果,幂函数的决定系数为0.477 4,高于其他模型。用已知检验点验证反演结果可知,实测粒径平均值为4.713 2 μm,反演粒径平均值为4.209 5 μm,最大绝对误差为3.840 1 μm,最小绝对误差为0.067 6 μm,平均绝对误差为1.137 9 μm。
5.2 清水区悬沙粒径遥感反演
5.2.1 悬沙粒径与单波段反演模型
借鉴本研究中4.2节清水区悬沙粒度数据与波段反射率的相关性分析结果,分别以Ⅱ波段、Ⅲ波段反射率R2,R3为自变量,数量中值粒径Zr为因变量,建立悬沙粒度反演模型,结果如表6所示。

表6 清水区Ⅱ波段、Ⅲ波段遥感反演模型
对比反演结果,单波段Ⅱ波段多项式模型决定系数最高,为0.910 2。随机抽选出5个检验点用以验证悬沙粒度遥感反演模型的精度,验证对比的结果是实测数量中值粒径平均值0.506 2 μm,反演粒径平均值0.509 2 μm;反演数量中值粒径最大值为0.573 2 μm,最小值为0.482 3 μm;最大绝对误差0.029 1 μm,最小绝对误差0.007 7 μm,平均绝对误差0.014 7 μm。
5.2.2 悬沙粒径与波段比遥感反演模型
以Ⅱ,Ⅲ波段比反射率A4为自变量,数量中值粒径D50为因变量,建立粒度遥感反演模型,结果如表7所示。

表7 清水区Ⅱ,Ⅲ波段比遥感反演模型
根据反演结果可知,决定系数最高的是多项式模型。用实测检验点验证反演结果可知,实测粒径平均值0.506 2 μm,反演粒径平均值0.490 1 μm,最大值0.540 4 μm,最小值0.468 4 μm;平均绝对误差0.016 0 μm。
5.3 悬沙粒径遥感反演结果分析
将实测粒度数据分为受采砂影响的浑浊区与未受采砂影响的清水区2种类型,分别对浑浊区和清水区的悬浮泥沙粒度与遥感反射率进行遥感反演。反演结果表明:浑浊区水域悬沙粒度反演模型以单波段Ⅳ波段和Ⅱ,Ⅲ波段比的幂函数反演效果最好,决定系数分别为0.387 4和0.477 4;Ⅱ,Ⅲ波段比遥感反演平均绝对误差为1.137 9 μm,低于单波段遥感反演平均绝对误差1.181 0 μm;波段比的遥感反演精度高于单波段反演精度。清水区悬沙粒度反演模型以单波段Ⅱ波段和Ⅱ,Ⅲ波段比反射率为自变量的多项式模型拟合度最佳,决定系数分别为0.910 2和0.563 7;反演精度单波段Ⅱ遥感反演平均绝对误差0.014 7 μm,Ⅱ,Ⅲ波段比平均绝对误差0.016 0 μm,波段比的反演精度略低于单波段反演精度。
对比表4—表7中浑浊区和清水区反演结果,从反演模型选择上来看,浑浊区最适合选择幂函数作为反演模型,清水区最适合选择多项式作为反演模型;从反演波段选择上来看,浑浊区最适合选择波段比作为敏感波段建立反演模型,清水区最适合选择单波段敏感波段建立反演模型;从反演精度上来看,清水区反演精度要高于浑浊区。
6 结 论
在参考其他研究的基础上将鄱阳湖分为浑浊区和清水区,根据不同时间段,不同区域对鄱阳湖悬浮泥沙实时光谱测量以及对不同分布模式下粒度参数的分析,分别找出浑浊区和清水区悬浮泥沙的敏感波段和适宜于反演的最佳分布模式和粒度参数,确定遥感特征因子,建立悬浮泥沙粒度的遥感反演模型,并找出最适宜于鄱阳湖悬浮泥沙粒度反演的模型;最后,用实测的粒度数据对遥感反演的结果进行精度验证。得出以下结论:
(1)在浑浊区水域和清水区分别是体积百分比众数粒径和数量百分比中值粒径与遥感光谱反射率相关性最优,在反演时适宜作为反演参数因子建立模型。
(2)浑浊区水域,单波段Ⅳ波段和波段比Ⅱ,Ⅲ波段是遥感反演的敏感波段,建立的反演模型中,幂函数反演效果最好。波段比Ⅱ,Ⅲ波段比单波段Ⅳ波段反演精度高。
(3)清水区水域,单波段Ⅱ波段和波段比Ⅱ,Ⅲ波段是悬沙粒度遥感反演的敏感波段,建立的反演模型中,多项式模型拟合度最好;单波段Ⅱ反演精度略高于波段比Ⅱ,Ⅲ波段。
(4)对比浑浊区和清水区反演结果,从反演模型选择上来看,浑浊区最适合选择幂函数作为反演模型,清水区最适合选择多项式作为反演模型;从反演波段选择上来看,混浊区最适合选择波段比作为敏感波段建立反演模型,清水区最适合选择单波段敏感波段建立反演模型;从反演精度上来看,清水区反演精度要高于浑浊区。
[1] 李占海,陈沈良,张国安.长江口崇明东滩水域悬沙粒径组成和再悬浮作用特征[J].海洋学报,2008,30(6):154-163.
[2] 恽才兴.遥感文集[M].北京:科学出版社,1981:99-109.
[3] 刘忠华,李云梅,吕 恒,等.基于偏最小二乘法的巢湖悬浮物浓度反演[J].湖泊科学,2011,23(3):357-365.
[4] HUANG Hai-jun, LIU Yan-xia, WANG Bo. Effect of Spatial and Spectral Resolution of Images on Interpreting Intertidal Estuarine Sediment Grain Size Distributions[C]∥Proceedings of the 30th IEEEE International Geoscience and Remote Sensing Symposium, Honolulu, USA, July 25-30, 2010: 13-16.
[5] DE C, CHAKRABORTY B. Estimation of Mean Grain Size of Seafloor Sediments Using Neural Network[J]. Marine Geophysical Research,2012,33(1):45-53.
[6] FAN Hui, HUANG Hai-jun. Remote Sensing Retrieval of Suspended Particulate Matter Concentrations of Surface Waters near Radial Sand Ridges Area in the South Yellow Sea[J]. Scientia Geographica Sinica, 2011,31(2): 159-165.
[7] 刘信中,叶居新,等.江西湿地[M].北京:中国林业出版社,2000.
[8] 闵 骞,时建国,闵 聃.1956—2005年鄱阳湖入出湖悬移质泥沙特征及其变化初析[J].水文,2011, 31(1):54-58.
[9] 张 鹏,陈晓玲,陆建忠,等.基于遥感的鄱阳湖丰水期悬浮泥沙数值模拟预测[J]. 武汉大学学报(信息科学版),2017,42(3):369-376.
[10] 唐军武,田国良,汪小勇,等.水体光谱测量与分析I:水面以上测量法[J].遥感学报,2004,8(1):37-44.
[11] 况润元,罗 卫,张 萌.基于实测数据与遥感影像的鄱阳湖湖水体光学分类[J].长江流域资源与环境,2015,24(5):773-780.
[12] 曾 群,赵 越,田礼乔,等.HJ-1A/1B卫星CCD影像水环境遥感大气校正方法评价研究——以鄱阳湖为例[J].光谱学与光谱分析,2013,32(5):1320-1326.
[13] PULLIAINEN J,KALLIO K,ELOHEIMO K,etal. A Semi-operative Approach to Lake Water Quality Retrieval from Remote Sensing Data [J].Science of the Total Environment,2001,268(1/3):79-93.
[14] 陈晓玲,吴忠宜,田礼乔,等.水体悬浮泥沙动态监测的遥感反演模型对比分析——以鄱阳湖为例[J].科技导报,2007,25(6):19-22.
[15] 李文红.鄱阳湖水体反射光谱分析及悬浮泥沙定量反演研究[D].赣州:江西理工大学,2014.
[16] 沈 芳,周云轩,李九发,等.河口悬沙粒径对遥感反射率影响的理论分析与实验观测[J].红外与毫米波学报,2009,28(3):168-172.
[17] BHARGAVA D S, MARIAM D W. Effects of Suspended Particle Size and Concentration on Reflectance Measurements[J].Photogrammetric Engineering and Remote Sensing,1991,57(5):519-529.
(编辑:罗 娟)
Models of Remote Sensing Retrieval of Suspended Sediment Particle Size in the Poyang Lake Based on Measured Spectral Reflectance Data
KUANG Run-yuan, XIE Jia, ZHANG Meng, LI Wen-hong, ZHANG Gang-hua
(School of Architectural and Surveying amp; Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China)
Particle size of suspended sediment, as an important parameter reflecting water quality, has an influence on the spectral reflectance of water. Study of the relationship between particle size and reflectance is of great significance to water environment monitoring in inland lakes. In this paper, the suspended sediment particle size of the Poyang Lake was retrieved using different mathematical models based on correlation analysis according to measured spectral reflectance data. Results show that: 1) volume percentage median diameter is suitable for the retrieval model for turbid area; while quantity percentage median diameter is suitable for clear water; 2) in turbid area, single band Ⅳ is the sensitive wave band; whereas in clear water, single band Ⅱ and single band Ⅲ are sensitive wave bands. In addition, the reflectance ratio of band Ⅱ to band Ⅲ is the sensitive wave band in the whole study area; 3) in the retrieval model of single band reflectance, power function is suitable for the retrieval of suspended sediment particle size in the Poyang lake; while in the model of band reflectance ratio, polynomial model is the most suitable.
Poyang Lake; particle size of suspended sediment; remote sensing reflectance ratio; quantitative inversion; sensitive wave band
10.11988/ckyyb.20160728 2017,34(11):132-137,147
2016-07-15;
2016-09-28
国家自然科学基金项目(41101322);江西省自然科学基金项目(20114BAB213022);江西省教育厅科技项目(GJJ160617)
况润元(1976-),男,江西上高人,副教授,博士,主要从事水环境遥感、地理信息系统应用等方面的研究,(电话)15216181496(电子信箱)rykuang@163.com。
TP79
A
1001-5485(2017)11-0132-06

