不同侧应力状态下混凝土循环加卸载损伤特性

, ,,

(1.三峡大学 土木与建筑学院,湖北 宜昌 443002； 2.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌 443002)

不同侧应力状态下混凝土循环加卸载损伤特性

刘博文1, 2,彭刚1, 2,马小亮1, 2,谢京辉1, 2

(1.三峡大学 土木与建筑学院,湖北 宜昌 443002； 2.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌 443002)

采用大型多功能液压伺服静动力三轴仪对不同单向恒定侧压下的混凝土进行应变速率为10-4s-1的等应变增量循环加卸载试验，恒定侧压为单轴静态抗压强度的0%,5%,10%。研究了不同侧应力水平下应力-应变全曲线中滞回环的变化规律，分析滞回环与耗散能的关系,并构建损伤估计模型，最后基于耗散能统计,研究混凝土的损伤特性。得出主要结论如下：①全曲线中滞回环在卸载初始阶段应力下降较快而变形恢复很慢，但随着应力的逐渐下降,应变恢复才开始加快；②在循环次数相同时，耗散能随着侧应力的增加而增加，且增加幅度明显，表明单位耗散能具有明显的侧应力敏感性；③建立的双参数损伤估计模型，能够很好地拟合循环加卸载损伤与累积残余应变的关系；④随着侧压比的提高，混凝土损伤发展速度逐渐减慢，损伤累积的路径大幅延长。

混凝土;滞回环；侧压比；耗散能；损伤估计模型；损伤演化

1 研究背景

混凝土结构在服役期间常处于复杂应力作用下，同时还会承受相应应力的循环作用，如机场跑道上飞机降落的冲击、桥涵隧道中车辆的来往、采油平台下海浪的往复等。研究循环加卸载作用下的混凝土力学性能与损伤机理更加符合实际工程情况，有利于提高人们对于混凝土建筑物抗震安全的认知水平和预判能力，为工程应用中动态荷载的混凝土结构的安全性能评价提供一定的理论依据，具有重大的现实意义。

自首次发现混凝土抗压强度存在率敏感性以来,混凝土在单轴和多轴应力状态下的动态力学性能受到国内外学者的关注，并有了较为完善的研究成果[1-5]。目前，在关于混凝土材料的循环加卸载的试验研究相对较少，但也取得了相应的成果。王四巍等[6]得出经过循环加载后塑性混凝土的抗压强度和峰值应变与单调直接加载相比有所降低。胡海蛟等[7]对混凝土进行动态循环加卸载试验得出峰值应力与弹性模量随加载速率的提高而增大,并基于Weibull统计理论的分段式动态损伤本构模型较好地拟合了试验数据。李同春等[8]通过应力-应变试验数据建立了以等效应变作为参变量的变四参数等效应变损伤模型。梁辉等[9]进行了不同加载速率下的循环加卸载试验，得出共同点轨迹线与包络线形状大体相似,并构建了全曲线方程数学模型。肖福坤等[10]对煤层进行单轴循环加卸载试验，分析了循环加卸载应力-应变曲线，循环次数与滞回环面积曲线，弹性应变能与滞回环面积关系等。赵闯等[11]开展了岩石在不同围压作用下循环加卸载试验研究，探讨了循环的耗散能、损伤变量、塑性变形等与循环次数、应力之间在不同侧应力作用下的相互关系。Xiao等[12]分别用不同方法定义了疲劳损伤变量，并分析研究了疲劳损伤变量在演变过程中的影响因素。刘杰等[13]进行了不同应力水平下岩石材料的循环载荷试验，分析了弹性模量、泊松比和残余应变等变形参数的变化规律，同时探讨岩石损伤破坏过程中能量的转化。

上述研究对混凝土等脆性材料在不同应力状态下循环加卸载的基本动态力学特性已经积累了一定的成果。基于此，为了进一步探究侧应力作用下混凝土循环加卸载的损伤特性，本文对不同侧压应力状态下的混凝土进行等应变增量循环加卸载(应变步长为0.2 mm)试验，分析试验应力-应变全曲线特征，研究滞回环面积与耗散能的关系，建立损伤估计模型，揭示损伤机理与变化规律。

2 试验设计

2.1 试件制备

本文均采用尺寸为300 mm×300 mm×300 mm的试件，水泥采用宜昌三峡水泥有限公司生产的42.5级普通硅酸盐水泥，以细度模数为2.3的连续级配天然河沙为细骨料，5～40 mm连续级配的碎石为粗骨料，拌合水为饮用自来水。表1为混凝土单位体积的材料用量。

表1 混凝土单位体积的材料用量Table 1 Material content of concrete per cubic meter

试件采用钢模浇筑，待浇注成型后，在室内自然环境下静置24 h后拆模并编号，按20～40 mm间距摆放在砂浆垫块上，标准养护28 d。

2.2 试验设备及试验过程

本文力学加载设备为三峡大学和长春朝阳试验仪器有限公司联合研制生产的10 MN大型多功能液压伺服静动力三轴仪，根据试验需要可分别或同时为试件提供竖向、水平向轴向力并实时自动采集数据及记录当前情况反馈相关信息，实现存储、处理试验数据同步进行。该系统还能执行事先编制好的循环加卸载指令。设备加载框架和指令控制器见图1。

图1 加载设备和EDC控制器Fig.1 Loading equipment and EDC controller

试验前将试件打磨平整放置在垫板上轴心物理对中，然后在混凝土侧向布置好传力垫板并校正，盖好上部垫板。试件加载面采用塑料薄膜与甘油减磨处理，然后将小车推进预定位置，调整好传力柱与试件位置后安装竖向变形计。

首先,试验进行预加载，采用EDC1控制指令使底盘上顶保证试件与上部传力柱充分接触，预施加荷载至10 kN后减小移动速率至荷载到20 kN后保持稳定。然后,通过EDC3控制指令进行水平向加载，待水平方向加载至10 kN以确保试件与水平传力柱充分接触后安装水平方向变形计，在控制端软件检测界面将水平变形修改为0，并将水平荷载调至试验设定值。最后,使用预先编写好的加卸载程序，直接调入，点击发送指令进行应变加载速率为10-4/s的加卸载试验。程序设置为等应变增量循环加卸载试验，分级加载步长为0.2 mm，加载以1.8 mm/min速度加压，加载至应变步长为0.2 mm后，以20 000 N/s速度进行卸载至20 kN，以此为循环，直至循环加卸载负荷使试件完全破坏，并保存试验数据。

试验所用混凝土试件单轴静态抗压强度平均值fc=33.25 MPa，按照恒定侧压为单轴静态抗压强度的0%，5%，10%，因此,试验侧压值分别取0，150，300 kN。

3 试验结果及分析

3.1 循环加卸载下曲线滞回环分析

不同侧应力水平下，混凝土加卸载的应力-应变关系曲线见图2。再加载曲线从应力为0的任一应变值开始再加载，直至与上一次卸载曲线相交，在此过程中便构成一个封闭的滞回环,见图3。

图2 侧压循环加卸载试验全曲线Fig.2 Curves of cyclic loading and unloading in the presence of varying lateral stress

图3 循环加卸载试验全曲线中的滞回环Fig.3 Hysteresis loops of stress-strain curve

在卸载曲线段，应力下降很快，应变恢复很少，随着应力值的逐渐减少，应变恢复才逐渐加快，最终应力卸载为0，轴向应变也不能恢复到初始值，这是应变恢复滞后现象。由于混凝土在高应变速率下，材料本身具有黏性性质，从而引起应变滞后于应力。在不同侧压比作用下混凝土的应力-应变曲线相似，均存在应变恢复滞后现象，且裂缝开展得越充分，残余应变越大，恢复变形滞后现象越严重。

产生上述现象的主要原因是混凝土在轴向加压过程中，随着应力的增大，裂纹扩展、贯通形成纵向裂缝，由于试件存在纵向裂缝在高压应力状态下不可能恢复，产生了不可逆的塑性变形，所以存在恢复变形滞后的现象。随着加卸载次数的增加，混凝土卸载后的残余应变逐渐增大，裂缝开展得越充分,恢复变形滞后的现象也越严重，卸载后可恢复的应变也越少。

由图2和图3得出：在侧应力为0 kN时，混凝土历经8次循环加卸载破坏；在侧应力为150 kN时，混凝土历经14次循环加卸载破坏；在侧应力为300 kN时，混凝土历经28次循环加卸载破坏。可见，随着侧压比的增加，混凝土历经加卸载破坏的循环次数增加，混凝土失稳破坏的路径被延长。

图4 侧压下试件最终破坏Fig.4 Photos of final destruction of specimens under varying lateral stress

混凝土在不同侧应力下的破坏形态不同，如图4所示。在单轴循环加卸载作用下呈柱状破坏，在150 kN和300 kN侧压下呈片状破坏。由于单轴加载下竖向发生压缩变形，水平向发生伸长变形，试件在轴向加压过程中首先靠近侧表面产生纵向裂纹;随着应力的增大，裂纹扩展、贯通形成纵向裂缝，随后裂缝逐渐向试件角部拓展，最终形成倒八字形裂缝，同时试件纵向裂缝在高压应力状态下不可能恢复，产生了不可逆的塑性变形，导致试件呈柱状破坏。而在双轴作用下，侧应力对纵向裂纹起到抑制作用，试件在垂直于自由面方向产生拉应变，从而混凝土呈片状破坏。

3.2 滞回环面积与耗散能的关系研究

混凝土的吸能能力为应力-应变曲线在达到最大应力时与应变轴围成的面积，而在混凝土的加卸载应力-应变曲线下，加载轨迹与应变轴围成的面积代表外力加载吸收的能量，卸载轨迹下的面积则为混凝土释放的弹性能。因此，这种差异表明外力所做的功一部分表现为混凝土的弹性应变能，另一部分能量则被耗散掉，则耗散能Φ即为滞回环的面积。本文对滞回环面积与循环加卸载次数N的试验数据进行了统计，结果见表2。

表2 应变10-4s-1时不同侧应力下的单位耗散能Table 2 Unit dissipation energy under different lateral stresses at 10-4s-1 strain rate 10-6J/mm3

注：α为混凝土侧向应力与单轴静态抗压强度的百分比值；混凝土单轴静态抗压强度fc=33.25 MPa

图5 不同侧应力水平下循环次数与单位耗散能关系Fig.5 Relationship between the number of cycles and the dissipative energy under different stress levels

建立循环次数与耗散能的关系图，将表2得到的滞回环面积依次连接形成一条轨迹线，得到不同侧应力水平下循环次数与单位耗散能的关系,见图5。

根据表2、图5得出：

(1) 有侧向应力作用时，耗散能与循环次数关系曲线呈现峰值回落，而无侧应力时无峰值回落。由于在循环加卸载过程中脆性材料的能量耗散过程就是材料内部损伤的发展过程[14],侧向应力作用时，混凝土在循环加卸载过程中耗散能最大,即塑性变形最大处表现出明显的脆性破坏现象。其原因在于，侧向应力对混凝土的裂缝开展起到了抑制作用，使混凝土能承受更大的荷载，产生更大的变形，从而表现出一定的塑性破坏，即有侧应力时耗散能与循环次数关系曲线呈现先增大后减小的变化规律。

(2) 对比不同侧应力下的单位体积耗散能，在无侧压时，混凝土在第8次循环下耗散能最大，为5.707 5；侧压比α=5%时，混凝土在第9次循环下耗散能最大，为13.359 2；侧压比α=10%时，混凝土在第11次循环下耗散能最大，为23.774 9。可见，随着侧应力的增加，加卸载过程中耗散的能量增加，即裂缝的产生扩展所需的能量随着侧应力水平的增加而增加，表明单位体积耗散能具有明显的侧应力敏感性。

(3) 随着侧应力水平的增加，最大耗散能所对应的循环次数增大；并且随着侧压力的增加，达到最大滞回环面积所需要的循环次数增多，所需的相对时间增长，混凝土从开始受压到完全破坏历经循环次数增多。

4 混凝土损伤估计模型与分析

4.1 损伤模型的选取

已知滞回环面积为加载曲线段与坐标轴围成的面积与上一次卸载曲线段与坐标轴围成的面积之差。通过滞回环面积反映混凝土在加卸载过程中损耗的能量值，而能量的损耗与混凝土的损伤存在反映与被反映的关系，为此通过对耗散能的统计，研究混凝土在循环加卸载下的损伤发展过程，构建损伤变量D,其表达式为

(1)

在循环加卸载过程中，累积残余应变是指每次循环对应的残余应变值的总和。残余应变值是指每一个循环加卸载过程中，当前循环加载阶段峰值对应的应变与其卸载阶段应力卸载到0的应变的差值。可根据定义在应力-应变全曲线中求得残余应变值与累计残余应变值。

Weibull在1939年提出了脆性破坏统计理论，该理论以链条模型为基础，认为材料结构是由很多随机性质的各种微单元组成[15]，而这些微单元之间互不相关，因此各单元的强度是一组互不相关的随机变量，在链条模型中，若其中最薄弱的一环发生了断裂，则链条就会断开，该单元首先发生破坏，从而结构发生破坏。假定它们服从某一概率分布，而整个结构的强度取决于最薄弱的单元强度。王春来等[16]假定混凝土材料在单轴受压状态下的强度服从Weibull分布，即:

(2)

D=F(ε)=1-exp[-(ε/ε0)m] 。

(3)

式中:ε为累计残余应变;ε0为材料达到峰值应力时的参考平均应变;m为材料的均质度;m,ε0均可通过拟合得到。

根据试验数据求得残余应变值与累计残余应变值，通过式(1)求得循环次数N对应的循环损伤值D。现运用已构建的模型拟合基于滞回环面积统计的损伤值D与累计残余应变的关系，拟合效果见图6。

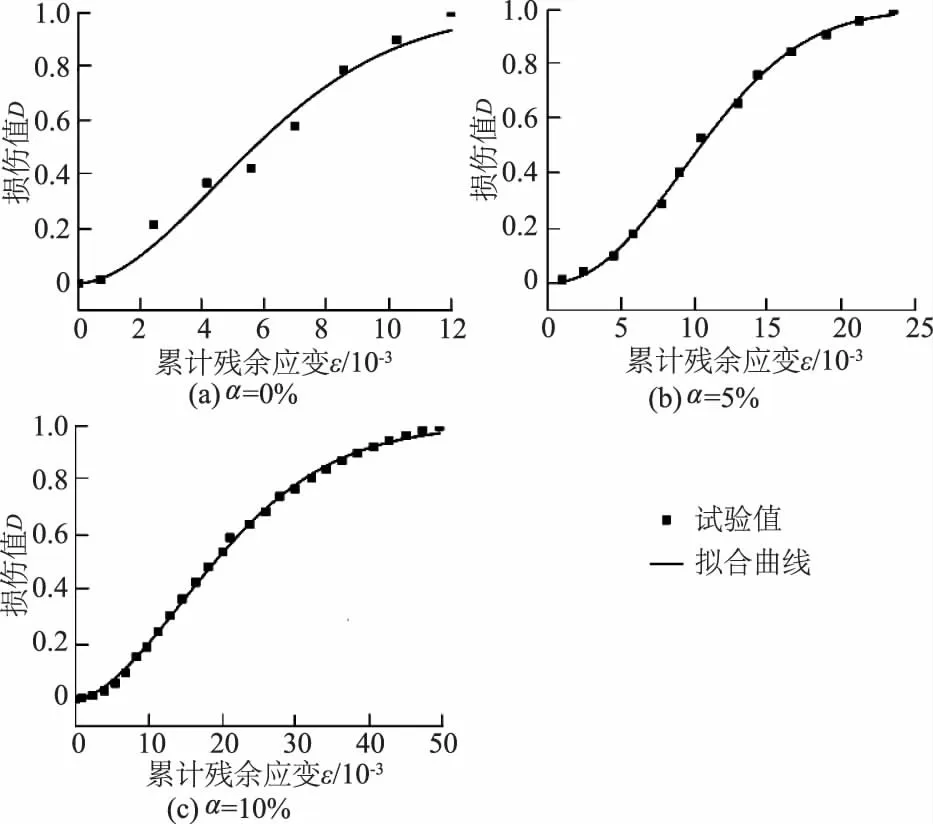
图6 不同侧应力水平下混凝土损伤值与累计残余应变试验拟合曲线Fig.6 Fitting curves of the relationship between damage value and cumulative residue strain under different lateral stress levels

由式(3)构建的损伤值D与累计残余应变关系的双参数模型的相关系数，在0%侧应力水平下：m=1.809,ε0=6.919，拟合系数R2=0.977；在5%侧应力水平下：m=2.174,ε0=12.348，拟合系数R2=0.998；在10%侧应力水平下：m=1.730,ε0=23.391，拟合系数R2=0.998。从拟合效果看，由式(3)拟合构建的双参数模型能很好地拟合混凝土循环加卸载损伤与累计残余应变的关系，并能够较好地运用在此类损伤分析中。

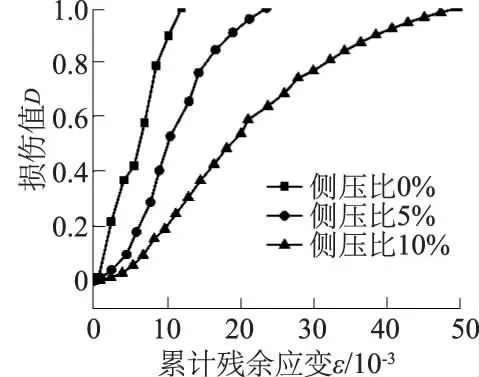
图7 不同侧压比下的混凝土损伤对比Fig.7 Comparison of concrete damage under different lateral pressures

4.2 损伤特性分析

图7为不同侧压比(0%,5%,10%)下的混凝土损伤对比图，由图7可知在0%侧压比作用下混凝土损伤曲线近似成直线，但随着侧应力水平的增加,损伤曲线逐渐向后推移，并大致相似呈“S”形，虽然损伤起始和终点是相同的，但其损伤发展演化路径不同。

随着侧压比的增加，混凝土的损伤发展速度逐渐减慢，损伤发展路径被延长。不同侧压比下，混凝土损伤发展的3个阶段出现明显的区别。相对于侧压比为10%，在侧压比较小时(0%，5%)，混凝土损伤发展初始阶段、损伤快速发展阶段和损伤发展失稳阶段的路径均较小。表明：侧压的存在对混凝土的损伤发展起到了抑制作用，延缓了混凝土内部裂纹的发展，增加了混凝土的延性性能。

5 结 论

(1) 滞回环在卸载曲线段随着应力下降应变恢复很慢，当应力卸载至本次循环最大应力的20%～30%以下时应变恢复最快，这是由于混凝土在高应变速率下具有黏性，从而引起应变滞后于应力的现象。

(2) 单位体积耗散能具有明显的侧应力敏感性：混凝土的单位体积耗散能随着侧应力的增加而增加，且增加幅度明显。同时随侧压力的增加，达到最大滞回环面积所需要的循环次数增多，混凝土从开始受压到完全破坏历经循环次数也增多。

(3) 基于滞回环面积统计的损伤值与累计残余应变的关系，构建与累积残余应变有关的损伤估计模型D=1-exp[-(ε/ε0)m]，该模型能很好地拟合混凝土循环加卸载损伤值D与累计残余应变的关系。

(4) 不同侧压下混凝土的损伤演化路径不同，随着侧压比增加,损伤曲线逐渐向后推移，由线性向“S”形演变。在0%侧压比作用下，混凝土的损伤累积近似成线性增长直至完全破坏；随着侧压比的提高，混凝土的损伤累计程度相对减小，损伤累积的路径被大幅度延长，曲线近似呈“S”形，直至进入破坏阶段。

[1] TEDESCO J W, POWELL J C, ROSS C A,etal. A Strain-rate-dependent Concrete Material Model for ADINA[J]. Computer and Structures, 1997, 64(5): 1053-1067.

[2] 关 萍.定侧压下混凝土双轴动态抗压性能的试验研究[J].土木工程学报,2009,42(4):33-37.

[3] 肖诗云，张 剑.不同应变速率下混凝土受压损伤试验研究[J].土木工程学报,2010,43(3):40-45.

[4] CAUSATIS G. Strain-rate Effects on Concrete Behavior [J]. International Journal of Impact Engineering, 2011, 38(4): 162-170.

[5] PERONI M, SOLOMOS G, VIACCOZ B,etal. Large-scale High Strain-rate Tests of Concrete[C]∥EPJ Web of Conferences. doi: 10.1051/epjconf/20122601030．

[6] 王四巍,高丹盈，刘汉东.循环加卸载下塑性混凝土强度及变形特性[J].工业建筑,2009,39(5): 92-95.

[7] 胡海蛟，彭 刚，谢玖杨，等.混凝土循环加卸载动态损伤特性研究[J].工程力学,2015,32(6):141-145.

[8] 李同春,杨志刚.混凝土变参数等效应变损伤模型[J].工程力学, 2011, 28(3): 118-122.

[9] 梁 辉,彭 刚，邹三兵，等.循环荷载下混凝土应力-应变全曲线研究[J].土木工程与管理学报,2014,31(4):55-59.

[10] 肖福坤,申志亮，刘 刚，等.循环加卸载中滞回环与弹塑性应变能关系研究[J].岩石力学与工程学报, 2014,33(9):1791-1797.

[11] 赵 闯，武 科，李术才，等.循环荷载作用下岩石损伤变形与能量特征分析[J].岩土工程学报,2013,35(5):890-896.

[12] XIAO Jian-qing, DING De-xin, JIANG Fu-liang,etal. Fatigue Damage Variable and Evolution of Rock Subjected to Cyclic Loading[J]. International Journal of Rock Mechanics amp; Mining Sciences, 2010, 47(3): 461-468.

[13] 刘 杰,李建林,张玉灯,等.循环荷载下岩体能量特征及变形参数分析[J].岩石力学与工程学报, 2010, 29(2): 3505-3513.

[14] 邓华锋，胡 玉，李建林，等. 循环加卸载过程中砂岩能量耗散演化规律[J]. 岩石力学与工程学报,2016,35(增1):2869-2875.

[15] 关 虓，牛荻涛，王家滨，等. 基于Weibull强度理论的混凝土冻融损伤本构模型研究[J]. 混凝土,2015,(5): 5-9.

[16] 王春来,徐必根,李庶林,等.单轴受压状态下钢纤维混凝土损伤本构模型研究[J].岩土力学,2006,27(1): 151-154.

(编辑：赵卫兵)

Dynamic Damage Properties of Concrete Subjected toCyclic Loading and Unloading with Different Lateral Stresses

LIU Bo-wen1,2, PENG Gang1,2, MA Xiao-liang1,2, XIE Jing-hui1,2

(1.College of Civil Engineering amp; Architecture, Three Gorges University, Yichang 443002, China; 2.Collaborative Innovation Center of Geological Hazards and Ecological Environment in Three Gorges Area in Hubei Province, Yichang 443002, China)

In this research, dynamic cyclic loading and unloading tests at strain rate of 10-4s-1under different unidirectional constant pressures are conducted on a large multi-functional static and dynamic force triaxial apparatus. Constant lateral pressures are 0%, 5%, 10% of the static uniaxial compressive strength. On this basis, the variation of hysteresis loop of stress-strain curve of concrete under cyclic loading and unloading with varying stress level is researched. The relation between dispersion hysteresis loop and energy dissipation is analyzed, and the damage estimation model is built. Furthermore, the damage characteristics of concrete are researched based on energy dissipation statistics. The following conclusions are obtained: 1) in initial unloading stage, the stress decreases rapidly and deformation recovers slowly, but the speed of recovery begins to accelerate with stress declining; 2) dissipative energy significantly increases with the increase of lateral stress under the same number of cycles, indicating that unit dissipated energy is apparently sensitive to lateral stress; 3) the damage estimation model of concrete is verified to perform well in fitting the relationship between damage and cumulative residue strain; 4) the development of damage decreases gradually with the increase of lateral pressure ratio, and in addition, the path of damage accumulation is greatly extended.

concrete; hysteresis loop; lateral pressure ratio; energy dissipation; damage estimation model; damage evolution

2016-07-04;

2016-09-11

国家自然科学基金项目(51279092)；三峡大学科研创新项目(CX2015025)

刘博文(1992-)，男，湖北宜昌人，硕士研究生，主要研究方向为混凝土材料动态特性，(电话)15071765653 (电子信箱)1696327945@qq.com。

彭 刚(1963-)，男，湖南岳阳人,教授，博士,主要从事混凝土材料与结构抗震方面的研究，(电话)13972604433 (电子信箱)871399412@qq.com。

10.11988/ckyyb.20160674 2017,34(11):121-125,131

TV502

A

1001-5485(2017)11-0121-05