涂覆石墨烯的电介质纳米盘的表面等离激元回音壁模特性

陈厚波， 邱伟彬 ， 黄艺馨， 唐一鑫， 邱平平， 王加贤， 阚强， 潘教青

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 中国科学院 半导体研究所， 北京 100083)

涂覆石墨烯的电介质纳米盘的表面等离激元回音壁模特性

陈厚波1， 邱伟彬1， 黄艺馨1， 唐一鑫1， 邱平平1， 王加贤1， 阚强2， 潘教青2

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 中国科学院 半导体研究所， 北京 100083)

提出涂覆单层石墨烯的电介质纳米盘结构，并利用有限元方法数值解析这种纳米结构的表面等离子激元回音壁模的电磁场特性.计算并分析品质因子(Q值)、模式体积随着电介质纳米盘半径大小、石墨烯化学势和谐振频率的变化规律.结果表明：当纳米盘的半径为5 nm，石墨烯化学势为0.9 eV时，其品质因子高达195，对应模式体积小于2×10-7(λ0/2n)3.

光学器件； 光学谐振腔； 表面等离子激元； 石墨烯； 回音壁模

近年来，电介质微谐振腔由于具有极好的本征回音壁模特性，如小的模式体积、高品质因子(Q值)、大的自由光谱和超紧凑的尺寸而受到广泛关注[1-3].迄今为止，微谐振腔已被证明在激光器和滤波器[4-6]中有重大应用.贵金属(如金、银)涂覆的谐振腔能够更好地提高其表面等离子激元(SPP)回音壁模(WGMs)的电磁场(EM)的限制能力，从而有效地减小器件的尺寸.然而，SPP场倏逝波的性质导致其额外的损耗，这个损耗使Q值减小.因此，为了在纳米谐振腔中保持表面等离激元回音壁模小的模式体积和高的品质因子双特性，必须找到一种同时满足高限制本领和低损耗的材料来覆盖电介质纳米腔.由单层碳原子组成的石墨烯由于具有奇特的力学、电子和光学特性[7-10]而引起人们广泛的研究.基于石墨烯的光学调制器[11]、纳机电系统(NEMS)[12]和晶体管[13-14]陆续被报道.在SPP领域，石墨烯也具有比传统贵重金属更加显著的优势，如低的传播损耗、高的电磁场限制能力.因此，石墨烯有望代替贵重金属，使纳米谐振腔能实现小的模式体积和高的Q值.本文提出并数值分析了掺杂的单层石墨烯覆盖的纳米电介质盘的等离子回音壁模特性，计算并分析模式体积和品质因子随着谐振腔的尺寸及石墨烯化学势的变化规律.

1 模拟方法与模型

整个结构由电介质纳米盘及其上下表面涂覆着的石墨烯层构成.在合适的频率和化学势下，石墨烯表现出金属性，可以像金属一样在电介质和石墨烯的界面出现表面等离激元.值得注意的是，由于石墨烯层只有单个原子层，可以利用表面电导率表征[15-17].在石墨烯片上，其表面电流密度定义为：J=σgE.式中:E和σg分别为电磁场中的电场和石墨烯的表面电导率.σg由带间电子跃迁和带内电子-光子散射两部分组成，即σg=σinter+σintra，根据Kubo公式[16，18]，石墨烯的表面电导率表示为

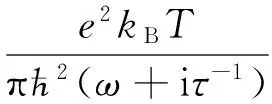
式(1)～(2)中：μc为石墨烯的化学势，可以通过改变化学掺杂或改变外电场进行调节[16，19]；τ为电子的动量弛豫时间.

从已有文献可知,石墨烯的化学势在温度低于250 K时，可以调高到2 eV[20].设定温度低于250 K，以确保高化学势是可实现的.同时，Low等[21]指出弛豫时间可以高达3 ps.对石墨烯而言，高的化学势和高的弛豫时间可以确保表面等离子波在高频率时，有高的限制和低的传输损耗.

利用有限元的分析方法对纳米盘的等离激元回音壁模式特性进行数值解析，所使用的软件是COMSOL Multi-Physics的RF模块.纳米盘的结构示意图，如图1所示.图1中:r和h分别代表电介质纳米盘的半径和高，r-R，h-H区域是空气.电介质纳米盘的上下表面涂覆石墨烯.

(a) 三维视图 (b) 俯视图 (c) 横截面剖视图图1 纳米盘的结构示意图Fig.1 Structural schematic diagram of nanodisk

对于纳米盘谐振器，有效模式体积[17，22]定义为

式(4)中：|E(r)|2和|H(r)|2分别代表电场和磁场度;ε(r)和μ0分别代表介电常数和磁导率.

Q值[22]是衡量纳米谐振器性能的重要参数之一，定义为

式(5)中：f=fRe+ifIm是模式的复数本征频率.模式数[17]的计算式为

式(6)中：λ0是电磁波在真空中的波长;neff是SPP波的有效折射率.

(a) 俯视图 (b) 正视图图2 纳米盘的典型等离子体回音壁模的电场Ez分布图Fig.2 Ez profile of typical SPP WGMs in dielectric nanodisk

2 结果与分析

2.1上下涂覆石墨烯的电解质纳米盘电磁场分布

典型的电磁场中,电场分量Ez的分布,如图2所示.图2中：纳米盘的半径和高度都是5 nm；电介质的有效折射率为3.45；石墨烯的化学势为0.9 eV；谐振频率为151 THz；对应在真空中的波长为1.98 μm.图2(a)表明了典型回音壁模式的特性.除此之外，由于化学势高达0.9 eV，因此,电磁场很好地被限制在单层石墨烯下方，如图2(b)所示.

表面等离子激元回音壁模的电场Ez方向剖面图随着模式数(m)变化的俯视图，如图3所示.当化学势为0.9 eV，半径为5 nm时，Q值和模式体积(Veff)随着模式数的变化，如图4所示.

(a) m=2(b) m=3(c) m=4(d) m=5

(e) m=6(f) m=7(g) m=8(h) m=9图3 纳米盘谐振器的表面等离激元回音壁模的电场Ez分布的俯视图Fig.3 Top view of Ez profile of SPP WGMs in nanodisk resonator

图4 Q值和模式体积随模式数的变化Fig.4 Q factor and effective mode volume as function of azimuthal number

图5 模式数和Q值随着纳米盘半径的变化Fig.5 Azimuthal number and Q factor as function of radius of nanodisk

2.2纳米盘几何参数的影响

在不同的频率下，模式数和Q值随着纳米盘半径的变化,如图5所示.图5中，模式数随着半径的增大而线性增大.一般来说，模式数与谐振器的半径成正比.如当频率为141 THz时，半径等于5 nm对应的模式数为6，半径等于30 nm对应的模式数为38.由图5可知：模式数和共振频率也成正比，特别是在大半径区域.当半径增大的时候，一方面,SPP波沿着圆周的传输损耗增大，Q值减小；另一方面，电介质纳米盘的限制能力增强，Q值增大.当两者相互补偿，Q值就会保持稳定.

当电介质纳米盘的高度发生变化时，模式数和Q值没有发生变化.这是因为在石墨烯层和电介质材料界面对电磁场具有极强的限制能力，光场被限制在石墨烯单层膜和纳米介质盘上下表面的界面处，从而使2个单层石墨烯之间的电磁场没有重叠部分.然而，只要选择合适的化学势、共振频率，那么，在电介质的上下表面电磁场会发生相互作用，这将使电磁场分布、模式数和Q值都受到高度的影响.

图6 在不同频率的条件下，模式数和Q值随着石墨烯化学势的变化关系Fig.6 Azimuthal number and Q factor as function of chemical potential with different resonant frequency

2.3石墨烯化学势的影响

当电介质纳米盘半径为10 nm,高度为5 nm，共振频率分别为141,151 THz时，模式数和Q值随着石墨烯化学势的变化，如图6所示.由图6可知:当化学势从0.6 eV增大到1.2 eV时，频率为151 THz所对应的Q值从110增加到220，而模式数从11减小到4.频率为141 THz时，也有类似的变化.

为了理解图6中Q值的行为，考虑等离子体沿着具有均匀化学势的石墨烯片传播，等离子体的传播常数强烈依赖于化学势与带间电子跃迁和带内电子-光子散射的阈值的差，即μc-1/2ћϖ[23].一方面，当μc高于阈值且保持增大趋势时，等离子体的传播损耗降低，Q值增大.另一方面，传播常数的实部可以写为neff·k0，它会随着化学势的增大而增大，等离子体的有效折射率neff增大，相应的模式数减小，与图6所示的结果一致.

2.4单层石墨烯的弛豫时间和电介质纳米盘的折射率的影响

Q值和模式数随着上下涂覆的单层石墨烯的弛豫时间的变化，如图7(a)所示.由图7(a)可知：对于一个给定的共振频率，当其他参数保持不变时，Q值和弛豫时间大致成正比.如当频率为161 THz，弛豫时间为0.5 ps时，对应的Q值为184；当弛豫时间为1.5 ps时，Q值变为554，该值甚至高于半径在微米量级、涂覆贵金属的微盘[24]对应的值.相比其他参数，弛豫时间是对于涂覆单层石墨烯的电介质纳米盘来说，决定Q值的最显著参数.Zhang等[24]指出，石墨烯的弛豫时间可以高达3 ps，在半径低于10 nm的情况下，如此高的弛豫时间意味着更高的Q值.而且，石墨烯的电子动量弛豫时间可以随着材料生长和纳米加工技术的发展进一步提高.因此，将来可以期望获得更高的Q值.在不同的频率条件下，随着弛豫时间从0.5 ps增大到1.5 ps，模式数保持稳定.这就意味着弛豫时间对模式体积没有明显的作用，当等离子体沿着单层石墨烯传播时，弛豫时间决定了等离子的损耗.同时，根据Gosciniak等[11]的报道，石墨烯的电子动量时间仅影响电磁场的重新分布速度，并不影响等离子体的电磁场定位.因此，提出的电介质纳米盘的电磁场分布并不被弛豫时间影响.

Q值和模式数随着电介质材料折射率的变化，图7(b) 所示.与涂覆单层石墨烯的化学势变化相比，电介质材料的折射率对于Q值和模式数的作用相反.对于141 THz的共振频率，当折射率为2.5时，模式数为2；当折射率为4.5时，模式数为6.在纳米谐振腔中，模式数可以用公式m=2neffπr/λ0估算.式中:neff是等离子体的有效折射率;λ0是真空中的波长.当电介质材料的折射率越高，等离子体的有效折射率也越高，因此,模式数也就越高，也意味着更好的限制能力.然而，只要定义单层石墨烯的几何结构和参数，等离子体沿着圆周的损耗也就确定.因此，折射率在一定范围内，Q值保持稳定.

(a) 弛豫时间 (b) 电介质纳米盘的折射率图7 Q值和模式数随着弛豫时间和电介质材料折射率的变化Fig.7 Q factor and azimuthal mode number as function of relaxation time and refractive index of dielectric nanodisk

2.5单面和双面单层涂覆石墨烯的比较

图8 模式体积随着单面和双面涂覆单层石墨烯的化学势的变化Fig.8 Mode volume as function of chemical potential with single and double coating

有效模式体积随着化学势的变化，如图8所示.图8中:纳米盘的半径为5 nm.由图8可知：当化学势从0.6 eV增大到1.0 eV时，双面涂覆单层石墨烯的纳米盘的模式体积大约是单面涂覆单层石墨烯的两倍.涂覆层对电磁场的限制能力很好，几乎所有的电磁场都被严格限制在纳米盘的石墨烯和空气的接触面里.在这2个接触面处，没有任何的相互作用，因此，当纳米盘的上下双面涂覆单层石墨烯的等离子体的模式体积是单面涂覆的两倍.然而，对于一些适当的共振频率和化学势，等离子体的电磁场限制能力比较差，可以诱导两个表面之间电磁场的相互作用，从而使得双面涂覆和单面涂覆的模式体积不是两倍关系.对于这两种情况，Q值没有任何明显的变化.

3 结束语

提出并数值分析了上下表面涂覆单层石墨烯的电介质纳米盘谐振器.数值计算结果表明：模式数、纳米盘的几何尺寸、电介质的折射率、涂覆的单层石墨烯的化学势、弛豫时间及单面或双面涂覆单层石墨烯对表面等离激元回音壁模的特性都有影响.随着模式数的增大，Q值增大，模式体积减小.随着半径的增大，模式数增大，而Q值保持稳定.这主要是由于半径增大，限制能力增强，同时，沿着圆周的表面等离子体的损耗增加，这两者作用相互抵消，因此，Q值不变.随着电介质折射率的增大，模式数增大，Q值保持稳定.随着化学势的增大，模式数减小，Q值增大.随着弛豫时间的增大，模式数不变，Q值增大.双面涂覆单层石墨烯的模式体积是单面的两倍，而Q值保持不变.

[1] YANG Yuede,HUANG Yongzhen,GUO Weihua,etal.Enhancement of quality factor for TE whispering-gallery modes in microcylinder resonators[J].Opt Express,2010,18(12):13057-13062.DOI:10.1364/OE.18.013057.

[2] YANG Yuede,HUANG Yongzhen,CHEN Qin.High-Q TM whispering-gallery modes in three-dimensional microcylinders[J].Phys Rev A,2007,75(1):13817.DOI:10.1103/PhysRevA.75.013817.

[3] BORISKINA S V,BENSON T M,SEWELL P D,etal.Directional emission, increased free spectral range, and mode Q-factors in 2-D wavelength-scale optical microcavity structures[J].IEEE J Sel Top Quant,2006, 12(6): 1175-1182.DOI:10.1109/JSTQE.2006.882662.

[4] QUAN Haiyong,GUO Zhixiong.Analyses of whispering-gallery modes in small resonators[J].Journal of Micro/Nanolithography, MEMS, and MOEMS,2009,8(3):33060.DOI:10.1117/1.3213247.

[5] MA Ning,LI Chao,POON A W.Laterally coupled hexagonal micropillar resonator add-drop filters in silicon nitride[J].IEEE Photonic Tech L,2004,16(11):2487-2489.DOI:10.1109/LPT.2004.835200.

[6] YANG Yuede,WANG Shijiang,HUANG Yongzhen.Investigation of mode coupling in a microdisk resonator for realizing directional emission[J].Opt Express,2009,17(25):23010-23015.DOI:10.1364/OE.17.023010.

[7] FALKOVSKY L A.Optical properties of graphene[J].Journal of Physics: Conference Series,2008,129(1):12004.DOI:10.1088/1742-6596/129/1/012004.

[8] CRACIUM M F,RUSSO S,YAMAMOTO M,etal.Tuneable electronic properties in graphene[J].Nano Today,2011,6(1):42-60.DOI:10.1016/j.nantod.2010.12.001.

[9] KOPPENS F H L,CHANG D E,DE ABAJO F J G.Graphene plasmonics: A platform for strong light-matter interactions[J].Nano Lett,2011,11(8):3370-3377.DOI:10.1364/OPN.22.12.000036.

[10] GRIGORENKO A N,POLINI M,NOVOSELOV K S.Graphene plasmonics[J].Nat Photonics,2012,6(11):749-758.DOI:10.1038/nphoton.2012.262.

[11] GOSCINIAK J,TAN D T H.Theoretical investigation of graphene-based photonic modulators[J].Sci Rep-UK,2013,3(7451):1897.DOI:10.1038/srep01897.

[12] SHI Zhiwei,LU Hongliang,ZHANG Lianchang,etal.Studies of graphene-based nanoelectromechanical switches[J] Nano Res,2012,5(2):82-87.DOI:10.1007/s12274-011-0187-9.

[13] WU Yanqing,LIN Yuming,BOL A A,etal.High-frequency, scaled graphene transistors on diamond-like carbon[J].Nature，2011,472(7341):74-78.DOI:10.1038/nature09979.

[14] XIA Fengnian,FARMER D B,LIN Yuming,etal.Graphene field-effect transistors with high on/off current ratio and large transport band gap at room temperature[J].Nano Lett,2010,10(2):715-718.DOI:10.1021/nl9039636.

[15] QIU Weibin,LIU Xianhe,ZHAO Jing,etal.Nanofocusing of mid-infrared electromagnetic waves on graphene monolayer[J].Appl Phys Lett,2014,104(4):41109.DOI:10.1063/1.4863926.

[16] HANSON G W.Dyadic Green′s functions and guided surface waves for a surface conductivity model of graphene[J].J Appl Phys,2008,103(6):64302.DOI:10.1063/1.2891452.

[17] ZHAO Jing,QIU Weibin,HUANG Yixin,etal.Investigation of plasmonic whispering-gallery mode characteristics for graphene monolayer coated dielectric nanodisks[J].Opt Lett,2014,39(19):5527-5530.DOI:10.1364/OL.39.005527.

[18] GUSYNIN V P,SHARAPOV S G,CARBOTTE J P.Magneto-optical conductivity in graphene[J].J Phys-Condens Mat,2007,19(2):26222.DOI:10.1088/0953-8984/19/2/026222.

[19] VAKIL A,ENGHETA N.Transformation optics using graphene[J].Science,2011,332(6035):1291-1294.DOI:10.1126/science.1202691.

[20] EFETOV D K,KIM P.Controlling electron-phonon interactions in graphene at ultrahigh carrier densities[J].Phys Rev Lett,2010,105(25):256805.DOI:10.1103/PhysRevLett.105.256805.

[21] LOW T,AVOURIS P.Graphene plasmonics for terahertz to mid-infrared applications[J].ACS Nano,2014,8(2):1086-1101.DOI:10.1021/nn406627u.

[22] XIAO Yunfeng,LI Beibei,JIANG X,etal.High quality factor, small mode volume, ring-type plasmonic microresonator on a silver chip[J].Journal of Physics B: Atomic, Molecular and Optical Physics,2010,43(3):35402.DOI:10.1088/0953-4075/43/3/035402.

[23] BAO Qiaoliang,LOH K P.Graphene photonics, plasmonics, and broadband optoelectronic devices[J].ACS Nano,2012,6(5):3677-3694.DOI:10.1021/nn300989g.

[24] ZHANG Xining,MA Zhe,YU Huakang,etal.Plasmonic resonance of whispering gallery modes in an Au cylinder[J].Opt Express,2011,19(5):3902-3907.DOI:10.1364/OE.19.003902.

(责任编辑： 黄晓楠英文审校： 吴逢铁)

SurfacePlasmonPolaritonWhispering-Gallery-ModePropertiesofDielectricNanodisksCoveredbyGrapheneMonolayer

CHEN Houbo1, QIU Weibin1, HUANG Yixin1, TANG Yixin1, QIU Pingping1, WANG Jiaxian1, KAN Qiang2, PAN Jiaoqing2

(1. College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China；2. Institute of Semiconductors, Chinese Academy of Science, Beijing 100083， China)

Graphene monolayer covered dielectric nanodisks are proposed in this paper. The surface plasmonic polariton whispering-gallery mode electromagnetic field properties of the proposed nano structures are numerically investigated by using finite element method. The quality factor, mode volume and Purcell factor of the optical modes are calculated as a function of dielectric nanodisks radius size, chemical potential of graphene and resonant frequency. Calculation results showed that a quality factor as high as 195, and a mode volume of less than 2×10-7(λ0/2n)3is achieved in a dielectric nanodisk with radius of 5 nm, where the chemical potential is 0.9 eV.

optical devices; optical resonators; surface plasmons; graphene; whispering gallery mode

10.11830/ISSN.1000-5013.201603030

O 436

A

1000-5013(2017)06-0842-06

2016-03-08

邱伟彬(1971-)，男，副教授，博士，主要从事低维材料微纳光子器件的研究.E-mail:wbqiu@hqu.edu.cn.

国家自然科学基金资助项目(6137805); 福建省泉州市科技基金资助项目(Z1424009); 中国科学院半导体重点实验室开放基金资助项目(KLSMS-1201)； 华侨大学研究生科研创新能力培育计划资助项目(1400201017)