CRM通信调制解调技术研究∗

潘 兵

（北京圣非凡电子系统技术开发有限公司 北京 102209）

CRM通信调制解调技术研究∗

潘 兵

（北京圣非凡电子系统技术开发有限公司 北京 102209）

论文采用了匹配滤波器和分数阶傅里叶变换对CRM（chirp-rate modulation）通信信号进行解调，推导了其理论解调误码率公式，将匹配滤波器解调和分数阶傅里叶变换解调的误码性能进行了对比分析；得到了影响解调性能的解析表达式，CRM通信信号抗多普勒频移能力较强，但对码同步误差较为敏感。通过仿真分析，验证了上述理论推导的正确性，分数阶傅里叶变换解调较匹配滤波解调性能差了约0.6dB～1.6dB，但其可避免载波恢复，大大简化了系统的同步设计。

CRM通信；匹配滤波器；分数阶傅里叶变换

1 引言

目前用于chirp调制技术主要有二进制正交键控（Binary Orthogonal Keying，BOK）调制和直接调制（Direct Modulation，DM）两种［1］，在Chirp-BOK调制中，chirp信号被用于表示调制后的符号，采用调频率携带信息，也即调频率调制（Chirp Rate Modulation，CRM）；而在Chirp-DM调制中，chirp信号仅用于扩展己调信号的频谱，采用相位携带信息。由于CRM通信信号通过匹配滤波器的输出具有明显的压缩脉冲［2］，能量被集中在很短的时间内，因此可以用匹配滤波器来进行解调；而chirp信号在分数阶傅里叶变换（Fractional Fourier transform，FrFT）域有很好的能量聚集性［3］，因此还可用FrFT来检测接收CRM通信信号能量聚集的峰值，以进行取样判决，恢复出数据。本文对CRM通信信号的上述两种解调方法进行研究，并对其进行性能仿真与分析。

2 CRM通信信号调制

2.1 chirp-rate调制原理

利用chirp信号进行数据传输的基本思想是把数据信息调制到chirp信号的各参数上，主要参数包括线性调频率、相位的正反极性、幅度的包络等。chirp信号的表达式为［4］

s(t)=a(t)cos(2πf0t+μπt2) -T/2≤t≤T/2 （1）

式（1）中 ，a(t)为 chirp信 号 的 包 络 ，a(t)=1,||t≤T/2、f0为chirp信号的中心频率、μ为调频斜率、T为chirp脉冲宽度，μ＞0时为up-chirp信号，μ＜0时则为down-chirp信号。如图1所示，chirp-rate调制通信时用up-chirp信号（正调频斜率）表示信码“1”，down-chirp信号（负调频斜率）表示信码“0”。图2为chirp-rate调制原理。

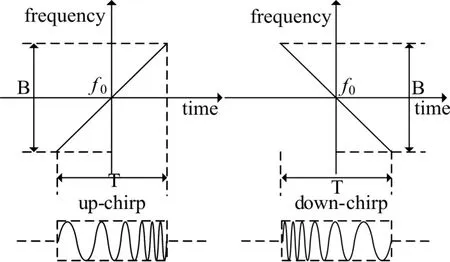
图1 up-chirp和down-chirp

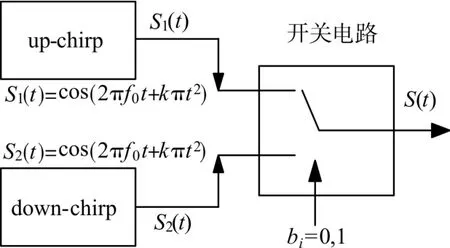
图2 chirp-rate调制原理

2.2 chirp-rate调制仿真

表1为本文chirp-rate调制参数，图3为chirp-rate信号的时域和频域波形。

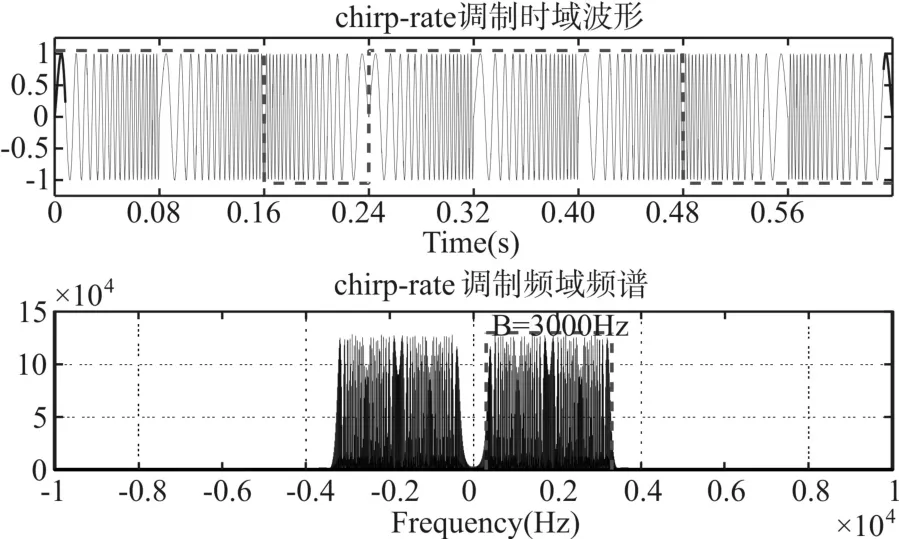
图3 chirp-rate调制信号的时域和频域波形

表1 chirp-rate调制参数

3 CRM通信信号解调

3.1 匹配滤波解调

3.1.1 匹配滤波解调原理

up-chirp信号和down-chirp信号具有尖锐的自相关特性，其相关函数为Sinc函数形式，up-chirp信号通过down-chirp匹配滤波器的输出脉冲压缩表达式为［5］

显然最佳的抽样判决时刻是在t=0时刻，包络取最大幅值为 TB。从式（2）可看出，信号的波形具有Sinc函数的特点，如图4（a）所示，主瓣时宽为2 B，其幅度为 TB；如图4（b）所示，压缩后峰值功率较未压缩时有 TB倍增益，该特性非常利于解调恢复信号。

图5比较了chirp信号通过匹配滤波器和非匹配滤波器的情况。可以看出，经匹配滤波的输出是明显的压缩脉冲，能量被集中在很短的时间内。而经非匹配滤波的输出没有被压缩，能量则均匀分布在时域上，因此抽样判决器可把对应的信号辨别出来。

图4 匹配滤波输出的波形

图5 chirp信号经匹配滤波输出波形

图6所示为chirp-rate调制解调系统框图，匹配滤波器通过比较输出峰值的大小判定接收信号是up-chirp信号或down-chirp信号，进而恢复出原始信息。

图6 chirp-rate调制解调系统框图

3.1.2 匹配滤波解调误码率

如图2所示，当发送信号为s1(t)时，经高斯白噪声信道后s(t)=s1(t)+n(t)（n(t)均值为0，方差为n02的高斯白噪声）。图6上支路匹配滤波器输出为

所以在高斯白噪声信道下，chirp-rate调制在匹配滤波接收时的平均误码率计算公式为

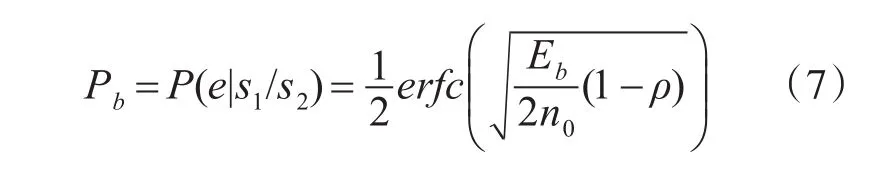
从式（7）可看出，chirp-rate调制系统的性能与up-chirp和down-chirp的互相关系数 ρ有关。当ρ=0时，两信号完全正交，系统误码率与chirp-rate相干解调误码率相同；当ρ=0.5时，系统误码率与传统BOK相干解调误码率相同［6］。在此本文给出互相关系数 ρ的表达式［7］为 ρ=C(D)/D ，（C(x)为Fresnel积分，D=TB为时宽带宽积）。表明互相关系数只与时宽带宽积D有关。由表1参数知D=T*B=240，代入互相关系数 ρ表达式可得ρ=0.032 接近0，即 s1(t)和 s2(t)准正交。图7（a）是互相关系数 ρ与时宽带宽积D的关系图，图7（b）是不同ρ值的误码率曲线图。

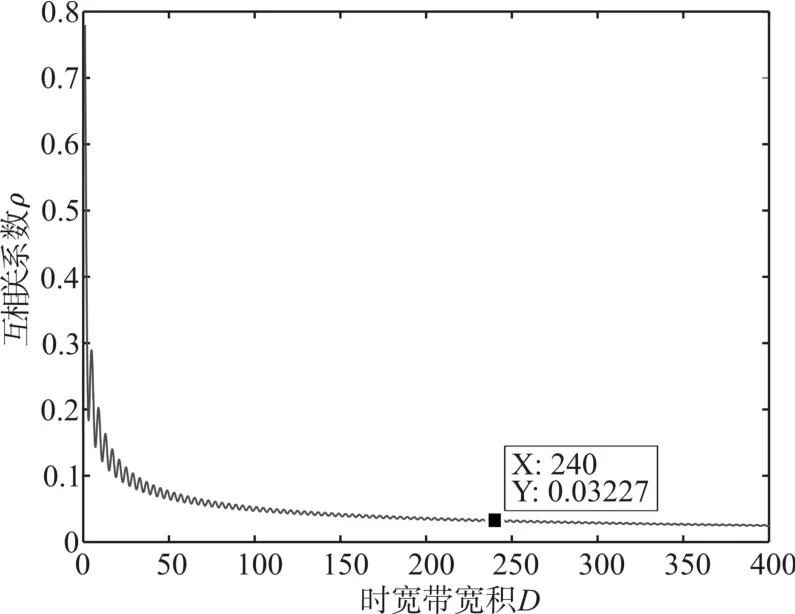
图7 （a） 互相关系数 ρ与时宽带宽积D关系

图7 （b） 不同 ρ 值的误码率

可见，ρ与 D有关，ρ越小，up-chirp和down-chirp信号越接近正交，系统性能也越好。从图7（b）可以看出，当 ρ=0.032时，BER曲线基本与ρ=0曲线重合，基本可认为是两路正交信号。在BER=10-4时，所需信噪比相差仅0.15dB左右。

3.2 分数阶傅里叶变换解调

3.2.1 分数阶傅里叶变换解调原理

分数阶傅里叶变换（FrFT）的基函数是分数阶域上一组正交的chirp基，一个chirp信号在特定的分数阶傅里叶域中将表现为一个冲击响应［8］。如图8所示，分数阶傅里叶变换在某个分数阶傅里叶域中对给定的chirp信号具有非常好的能量聚敛特性。

图8 （b）down-chirp信号任一阶次分数域波形

实chirp信号的分数阶Fourier谱与相同参数复chirp信号的分数阶Fourier谱是一样的，只是能量降低一半，多了一个对称普。在实际通信系统中，复信号可通过I，Q两路实信号来产生［9］。从分析信号的分数阶Fourier谱的角度出发，可用复信号模型来替代实信号模型。设基带chirp信号x(t)=Aexp(j2πf0t+jπkt2+jφ)，则其分数阶 Fourier变换为Xα(μ)

对于给定的基带信号形式，可以事先计算出“1”、“0”码元相应峰值的分数阶Fourier域采样位置值um如图9所示，从而在接收端直接在该点进行采样判决。

从图9中可以看出无论是复chirp信号还是实chirp信号在最佳阶数的FrFT均产生尖峰脉冲，但尖峰脉冲的位置不同，因此可通过这一区别实现基于FrFT的解调。

根据实chirp信号和图9所示的实chirp信号的分数阶傅里叶谱特点，可得到本文的FrFT解调方式，如图10所示。

1）将接收后的信号混频到基带，再将实基带信号按每个码元周期做 p阶FrFT变换处理；

2）对变换结果取模平方后，按照预先确定的采样位置um1、um0进行采样判决。

当 k=-cotα、f0=ucscα时，得到 x(t)的分数阶Fourier幅度谱峰值输出为

图9 码元1和0对应Chirp信号的FrFT

图10 FrFT非相干解调

3.2.2 分数阶傅里叶变换解调误码率

在加性高斯白噪声信道条件下，解调器输入端的接收信号为 y(t)=x(t)+n(t)。x(t)为发送信号，n(t)是方差为的高斯白噪声，y(t)服从高斯分布。由于FrFT为线性变换，因此对信号作 p阶FrFT等价为将信号通过参数为 p的线性滤波器，高斯过程通过线性系统后仍服从高斯分布［10］。当发送“1”码时，有：

式（14）即为本文推导出的FrFT解调的理论误码率计算公式。

4 CRM通信解调性能分析

4.1 误码率性能分析

图11所示为CRM通信的匹配滤波解调和FrFT解调的误码率仿真和理论曲线。

图11 高斯白噪声下CRM通信误码率性能

图11结果表明，式（14）表示的理论曲线与实际仿真结果基本吻合，验证了FrFT解调理论公式的正确性。另外，从图中可以看出在BER=10-5～10-2时，FrFT解调比匹配滤波解调有约0.6～1.6dB的性能损失。由于FrFT解调属于非相干解调方式，该结论是在预料之中的。（注：为使FrFT仿真解调性能接近于FrFT理论解调性能，需合理设计CRM通信参数使已调信号相位连续，需设置chirp-rate信号中心频率与信号时宽乘积为正整数）。

本文所采用的FrFT算法是目前复杂度最小的DFrFT算法-Close-form算法［12］。

4.2 相位误差对CRM通信解调性能的影响

4.2.1 相位误差对匹配滤波解调性能的影响

若存在码同步误差τ，输入chirp信号变为x(t)=Aexp(j2πf0(t-τ)+jkπ(t-τ)2)。

经过匹配滤波后，计算得出存在码同步误差的

普勒频移效果，对移动通信中抗多普勒效应具有良好的抑制效果。

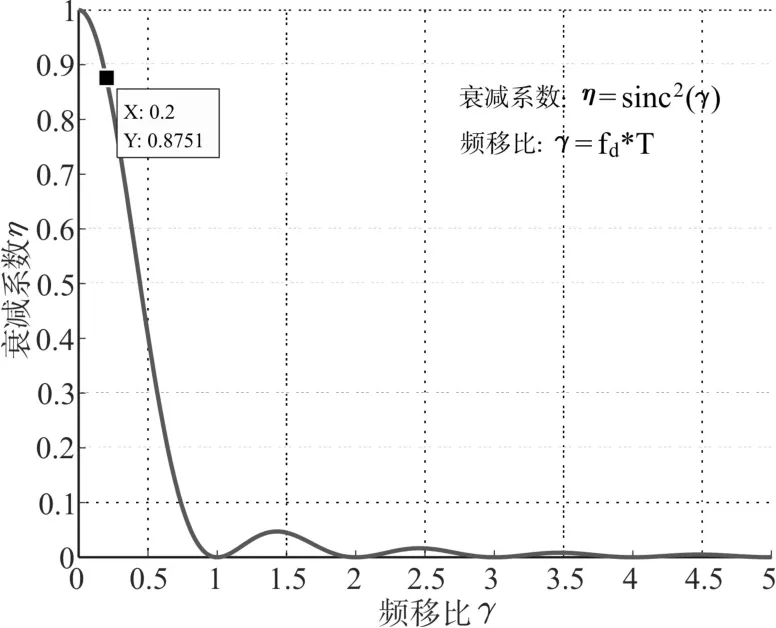
图12 衰减系数与频移比的关系

对上述解调方式进行了简单总结，得到表2如下。

5 结语

本文对CRM通信的两种解调方式进行理论研究与仿真分析，FrFT解调算法比匹配滤波法性能稍差，但匹配滤波（相干解调）需要严格估计载波的频偏和相位，同步系统设计繁琐，运算复杂度大。FrFT解调虽然比匹配滤波法相差0.6dB～1.6dB，但它对相位误差影响小，且多普勒频移与码同步误差的影响近似，FrFT解调属于非相干解调，因此可避免载波恢复，这使得系统的同步设计大大简化。由于CRM通信本身属于一种扩频通信体制（如本文扩频增益约24dB），因此CRM通信可应用于短波极低速（如本文信息速率为12.5bps）抗干扰隐蔽通信方面，具有很强的抗侦察抗截获能力。

表2 FrFT解调与匹配滤波解调的比较

［1］Zhuang Weihua，Shen Xuemin，Bi Qi． Ultral wideband wireles communications［J］.Wireless Communications and Mobile Computing，2003（3）：663-685.

［2］Ji W L，Zheng G X，Bao M Q，etAl.Ultra-narrowband wireless communication technology based on QVMCK modulation［C］∕Proc． of China-Japan Joint Microwave Conference，2008：164-166.

［3］陶然，邓兵，王越.分数阶傅里叶变换及其应用［M］.北京：清华大学出版社.2009：32-33.

［4］郑森，郑继禹，仇洪冰，王玫.现代扩频通信［M］.西安：西安电子科技大学出版社.2013：127-128.

［5］贺鹏飞.基于Chirp-BOK调制的超宽带无线通信系统研究［J］.南京邮电大学学报，2006，26（2）：21-25.

［6］Proakis J G．On the probability of error for multichannel reception of binary signals［J］.IEEE Trans． Commun.Technol，1968，COM-16（1）：68-71.

［7］潘兵.基于变时宽的CSS扩频通信新技术［J］.现代军事通信，2016，24（1）：15.

［8］Pei S C，Yeh M H，Tseng C C.Discrete Fractional Fourier Transform Based on Orthogonal Projections［J］.IEEE Transactions on Signal Processing，1999，47（5）：1335-1348.

［9］刘锋.分数阶Fourier变换中量纲归一化因子的选取［J］.系统工程与电子技术，2011，33（2）：237-239.

［10］刘建成，刘忠，王雪松.高斯白噪声背景下的LFM信号的分数阶Fourier域信噪比分析［J］.电子信息学报，2007，29（10）：2337-2340.

［11］曹志刚，钱亚生.现代通信原理［M］.北京：清华大学出版社，1992：276-278.

［12］Soo-Chang Pei，Jian-jiun Ding． Closed-form discrete fractional and affine Fourier transform［J］.IEEE Trans．on SP，2000，48（5）：1338-1353.

Research on CRM Communication Modulation and Demodulation Technology

PAN Bing
（Beijing Sheng Fei Fan Electronic System Technology Development Co.，Ltd，Beijing 102209）

This paper adopted the matched filter and fractional Fourier transform of the CRM（chirp rate modulation）communication signal demodulation，and its theory of demodulation error rate formula is deduced，the matched filter demodulation and the ber performance of fractional Fourier transform demodulation is analyzed.The analytical expressions that affect demodulation performance are obtained，and the communication signal of CRM is better than that of doppler shift，but it is sensitive to code synchronization error.Through the simulation analysis，validate the correctness of the theoretical derivation，the fractional Fourier transform demodulation is matched filtering demodulation performance difference is about 0.6dB～1.6dB，it can avoid carrier recovery，greatly simplifies the system design of synchronization.

CRM communication，matched filter，fractional Fourier transform

TN91

10.3969∕j.issn.1672-9730.2017.10.013

Class Number TN91

2017年4月8日，

2017年5月26日

潘兵，男，硕士研究生，工程师，研究方向：通信信号处理。