基于异构多核可重构系统的矩阵求逆设计与实现∗

钱庆松

（昆明船舶设备研究试验中心 昆明 650051）

基于异构多核可重构系统的矩阵求逆设计与实现∗

钱庆松

（昆明船舶设备研究试验中心 昆明 650051）

矩阵求逆是一种常见的计算密集型信号处理算法，广泛应用于声纳探测、雷达等高实时性要求的数字信号处理领域。随着多核芯片技术的成熟，其强大运算能力提供了一种全新的矩阵求解途径。论文在基于NoC的异构多核可重构系统上，映射了一种高斯消去法与上下三角矩阵分解（LU分解）法相结合的矩阵求逆方法。通过权衡系统并行度，核内存储空间和系统处理速度等多方面因素，进行并行算法分解、组合和任务分配，实现了64维以下任意维的复数矩阵求逆。

矩阵求逆；LU分解；异构多核；算法映射

1 引言

现代探测声纳发展呈现运算量大、实时性强及小型化的趋势［1］，因而对声纳的信号处理平台提出了越来越高的要求，高性能处理器在声纳信号处理中发挥的作用日趋重要，对其运算能力和数据吞吐能力的要求也越来越高［2］。基于可重构技术的片上多核处理器是一种将可重构技术与片上多核系统（Multi Processor System-on-Chip，MPSoC）相结合的硬件方案，利用集成片内的可重构硬件的可编程特性，可以针对不同的应用特征，定制片上数据路径。通过提高算法与硬件结构间的适配性，充分利用其并行计算处理能力，在确保数据吞吐率及处理速度情况下，具有更高的使用灵活性，有效地满足数据密集型和计算密集型任务的要求［3～5］。

在数字信号处理领域，矩阵求逆运算是一项非常重要的基本操作，广泛应用于通讯、导航、水下探测和雷达等领域。矩阵求逆的方法很多，比如初等变换法、伴随矩阵法、分块矩阵法等［6］。目前多使用定制专用硬件加速模块方法实现其快速求解，矩阵求逆计算的强数据相关性的特点给算法在多核系统中的实现带来了很大挑战，这在处理大维数矩阵时表现的更加显著［7～9］。本文在一种基于NoC的异构多核可重构系统，结合已有的三角矩阵求逆硬件实现方法、高斯消去法和矩阵的LU分解算法，探索了一种易在多核系统上以较高并行度执行的复数矩阵求逆方法。充分的利用异构多核系统的并行性，提高计算效率，保证计算结果具有较高精度。

2 算法分析

矩阵的一种比较常用的分解方法是矩阵的LU三角分解，将一个n阶矩阵A分解为一个下三角矩阵L和一个上三角矩阵U的乘积［7］。对上下三角矩阵求逆是非常方便的，可以利用这一特性减少求任意n阶矩阵A的逆矩阵的运算量和复杂度。具体的流程为：首先对矩阵进行LU分解，然后对L和U矩阵求逆得到L-1和U-1，最后通过矩阵乘积求得原始矩阵A的逆A-1=U-1L-1。

2.1 矩阵的LU分解［6］

高斯消去法可行的充要条件是方程（3）的系数矩阵A的所有顺序主子式Di≠0,i=1,2,…,n，本文硬件求逆方法所适用的矩阵也需满足这一条件。其中，高斯消去法包括消元和回代两个过程，本文只利用了消元过程，故回代过程就不做赘述。

2.3 矩阵求逆

将待解矩阵A右接一单位矩阵E，得到(A,E)。利用矩阵的初等行变换对(A,E)进行高斯消元过程得到(U,B)，易知B=L-1。同样，将U右接一单位矩阵(U,E)，进行初等变换得到(E,U-1)，最终得到原始矩阵A的逆矩阵A-1=U-1L-1，完成整个矩阵求逆的过程。

3 异构多核可重构系统

ReMPSOC是一款可编程异构多核SoC处理系统，结构简单，具有极大的数据吞吐量级计算核集成度，主要面向高密度计算应用。本系统不仅适用于某些特殊类型运算，并具有一定的通用性［10］。

系统结构图［11］如图1所示，系统中包含通信网络、主控单元（MC）、计算单元（Cluster，C）、接口单元及存储模块（MEM），不同的功能单元（以下称为簇）连接在不同的mesh网络的路由节点上，完成控制、运算、接口通讯、访存等任务。每个簇分别有一个状态上传接口、一个配置下达接口、PCC数据接口；簇间通过状态网络、系统主控制器及配置网络传递控制信息；通过PCC网络传输运算数据。运算簇实现数据运算，并提供符合IEEE 754标准的32位单精度浮点运算能力。运算簇包括两种：可重构计算单元（RCU）运算簇、协处理器（COP）运算簇。

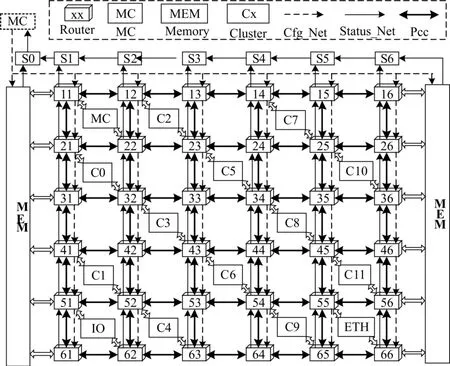
图1 多核系统芯片结构示意图

1）RCU运算簇［10］

RCU运算簇提供符合IEEE 754标准的32位浮点运算能力，主要完成规则的浮点复数∕实数运算，包括复数乘、复实乘、矩阵乘、乘法、加减法等运算。RCU运算簇具有可重构特性，采用2PE结构，支持存储运算和流运算两种运算模式。

2）COP运算簇

COP运算簇提供符合IEEE 754标准的32位浮点运算能力，主要完成非规则的浮点复数∕实数运算，包括：乘法、加减法、除法、开方、正余弦等运算。COP运算簇基于SIMD架构，采用Microblaze作为运算的控制单元，并采用符合Microblaze的DFSL接口协议的硬件浮点运算协处理器作为加速单元，能够同时完成2路32位宽的浮点运算。

4 算法映射

本文映射的是基于高斯消元法和LU分解法的64维复数矩阵的求逆，分5个任务完成整个求逆过程，各个任务的源数据、结果数据和及功能可从图2看出，其中Λ为一对角矩阵，U'为一下三角矩阵。通过修改配置信息和软件代码中的循环次数可实现64维以下任意维复数矩阵的求逆。

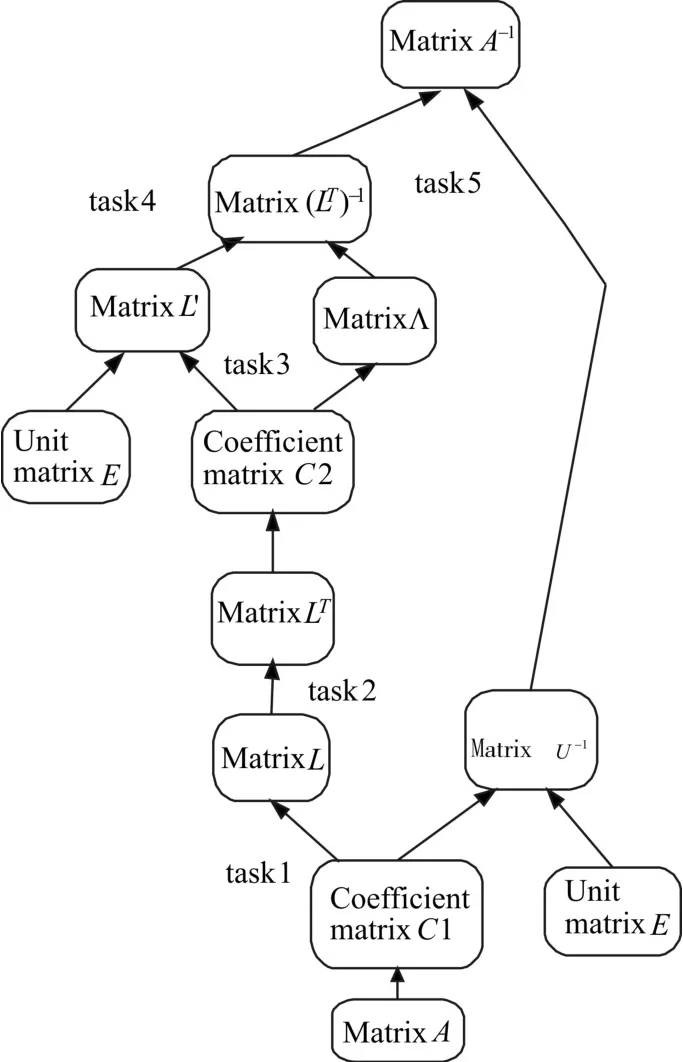
图2 矩阵求逆流程图

4.1 求解U-1和L过程的映射

为了方便起见，以式（3）中的 A=A(0)为例，task1为计算下三角矩阵L并根据消元过程中得到的系数矩阵，并根据系数矩阵对单位矩阵进行列变换得到U-1。计算下三角矩阵和进行列变换时，都是基于高斯消元方法，具体的计算过程是通过不断地循环完成的，每一次循环完成对A矩阵中一列元素的消元。该过程属于计算密集型运算，前后数据相关性大，计算不规则，因此采用具有较强的本地运算能力和灵活的地址控制机制COP完成主要操作。task1的任务映射图如图3所示。以64维矩阵为例进行说明，整个消元过程是通过63次大的循环完成的，以第一次循环为例：COP0首先向MEM存储单元请求原始矩阵A，计算消元系数

将系数向量通过数据网络传递给COP1、COP2同时写回MEM存储单元；COP1和COP0分别用于根据系数矩阵求下三角矩阵L和对单位阵进行列变换求U-1，避免对系数矩阵的重复读取而降低运算效率。COP1、COP2进行复数乘，将对应的系数乘以第一列；RCU0、RCU1执行复数加即消元过程，当RCU0和RCU1复数加任务完成时也就说明第一列的消元已经全部完成，这时COP0会向MEM存储单元请求新生成的矩阵执行第二次循环。图4用伪码表示了整个消元过程。

图3 高斯消元过程伪码

图4 task1任务映射图

4.2 求解LT过程的映射

task2对task1得到的L矩阵进行转置操作。为了充分的利用系统中的运算簇以提高算法的执行效率，本文采用分块转置的方法，其公式如下。

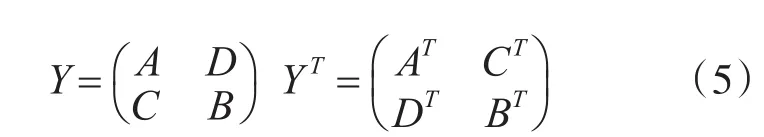
在转置过程中将原矩阵分为四块，对其中的每一块进行转置操作。在转置任务时，使用具有灵活地址跳变规律的COP进行转置运算，task2中使用4个COP并行执行转置操作，每个COP对其中的矩阵中的一块进行转置，然后将计算完成的结果写回DDR存储单元，以作为后续操作的源数据。task2的任务映射图如图5所示。

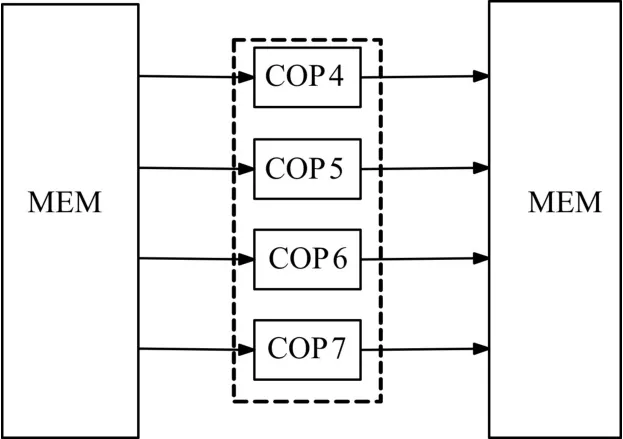
图5 task2任务映射图

4.3 U-1L-1的映射

根据任务分解图可以得知，task3与task1的操作基本相同，仅是源数据和结果数据不同，因此task3与task1的任务映射图相同。task3根据task2转置得到的LT，使用相同的计算方式得到一对角矩阵Λ和一下三角矩阵L'。task4将L'的每一列除以矩阵Λ相应行中对角线上的元素，得到(LT)-1在RCU和COP中，只有COP支持复数除法操作，为了提高运算效率，依然使用4个COP进行相除计算，任务映射图与图4基本相同。

task5将LU分解得到的两个结果相乘，进行U-1L-1计算，完成整个求逆操作。在task4中得到的结果为(LT)-1，在计算过程中，不再对(LT)-1进行转置操作，而是直接按其逆矩阵的形式取出与L-1执行矩阵乘操作。矩阵乘任务为比较规整的任务，为了充分的使用系统中的运算簇，此任务使用8个RCU执行并行计算，RCU根据其地址控制机制对输入的数据进行乘累加，最后将A-1写回MEM存储单元。

5 实验和结果分析

本次实验是在Xilinx公司Virtex7系列的XC7V2000T FPGA芯片上实现的，工作频率为100MHz。实验结果通过网口簇上传至主机，并与MATLAB软件计算结果进行了对比，绝对误差为10-4，整个计算过程共需要907222个时钟周期，其中包括了数据传输时间。以下是各个任务所消耗周期数：

图6 task5任务映射图

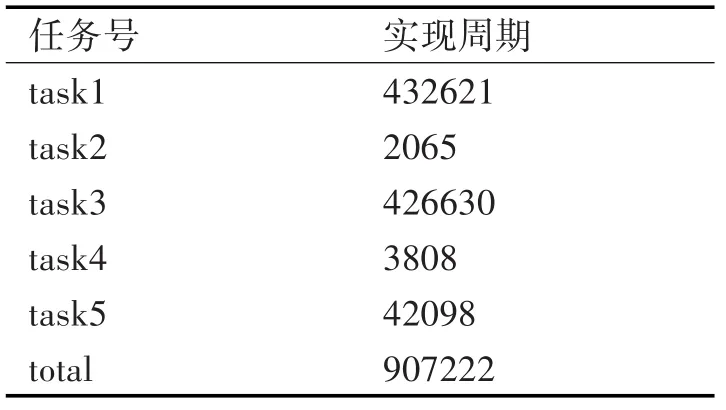
表1 矩阵求逆中各任务的计算时间

为了方便对实验结果进行的分析，直观的表示计算效率，以不同任务的并行度DP表示系统的计算效率，并行度定义如公式6所示［12］。

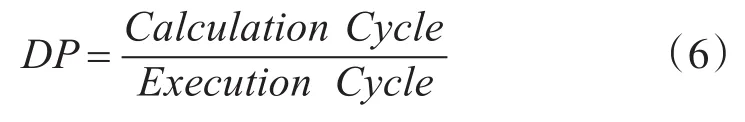
在公式中，Calculation Cycles表示任务计算过程中所需的计算周期，Execution Cycles表示完成整个任务所消耗的周期数。各任务的计算并行度如表2所示。

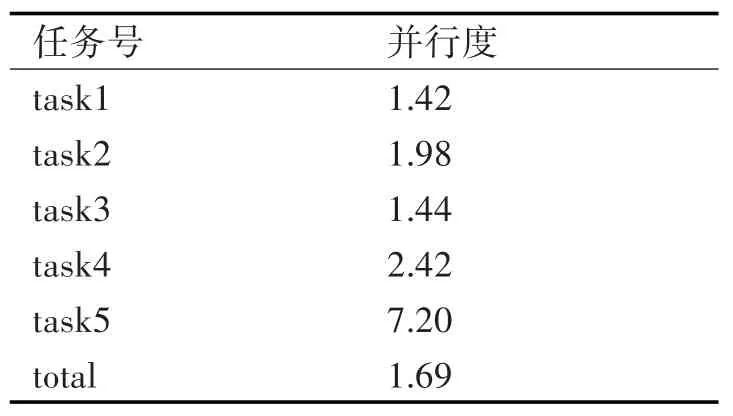
表2 矩阵求逆中各任务的并行度

在本文的映射方案中，对于64维以下的矩阵求逆只需改变task1中的循环次数及部分数据信息即可，具有较好的灵活性。计算过程中任务计算的并行度不仅与参与运算的运算簇有关，还与计算任务的类型有关，从表2可以看出，task1由于计算过程中前后数据相关性大，且整个计算过程需要不断的循环完成，任务并行度相对较低。在task5中，计算过程中没有数据相关性且充分的利用系统中的运算簇，任务并行度达到最高，也反应出系统对于规则运算的良好适应性及计算效率。

6 结语

在数字信号处理领域，研究在大维数矩阵求逆中减少运算时间，提高运算效率具有重要意义。本文通过对矩阵求逆算法的理论分析，提供了一种基于异构多核可重构系统的硬件复数矩阵求逆解决方案，并在FPGA开发板上验证了其正确性。

通过实验结果分析可得，系统性能仍有较大的提升空间，为了得到更高的处理速度和任务并行度，可以增强和改善多核系统中各个运算簇的功能，减少求逆过程中不必要的运算。进一步研究矩阵求逆的算法，加强矩阵求逆算法的并行度，提高加速效果等，对于研究多核芯片技术具有重要意义。

［1］任宇飞，袁俊舫，李峥，等.多核DSP在无人平台探测声纳中的应用研究［J］.应用声学，2014，33（6）：496-504.

［2］张晓燚.基于多核DSP的阵列信号处理系统设计［D］.北京：中国科学院大学，2015.

［3］Chen F Y，Zhang D S，Wang Z Y.Research of the Heterogeneous Multi-Core Processor Architecture Design［J］.Computer Engineeringamp;Science，2011，33（12）：27-36.

［4］ Ju R.A Hardware∕Software Method for Heterogeneous Cores Cooperating on Stream Architecture［J］.Chinese Journal of Computers，2008，31（11）：2038-2046.

［5］杜高明.MPSoC-NoC多核体系结构及原型芯片实现技术研究［D］.合肥：合肥工业大学，2007.

［6］苏育才.萎翠波，张跃辉.矩阵理论［M］.北京：科学出版社，2006：166-172.

［7］郭春煊，毛志刚，谢憬，等.矩阵求逆运算的VLSI实现［J］.计算机技术与发展，2008，18（5）：219-223.

［8］王锐，胡永华，马亮，等.任意维矩阵求逆的FPGA设计与实现［J］.中国集成电路，2007，16（4）：51-56.

［9］李涛，张忠培.矩阵求逆的FPGA实现［J］.通信技术，2010，43（11）：147-149.

［10］Wang Xing，Zhang Duoli，Song Yukun，et al.Design and Implementation of a reduced floating-point reconfigurable computing unit［C］∕International Conference on Computer，Network Security and Comunication Engineering，2014.

［11］SONG Y，JIAO R，ZHANG D，et al.Performance analysis for matrix-multiplication based on an heterogeneous multi-core SoC［C］∕ASIC，2015 IEEE 11th International Conference on.IEEE，2015：1-4.

［12］张多利，沈休垒，宋宇鲲，等.基于异构多核可编程系统的大点FFT卷积设计与实现［J］.电子技术应用，2017，43（3）：16-20.

Design and Implementation of Matrix Inversion on Heterogeneous Multicore Reconfigurable System

QIAN Qingsong
（Kunming Shipborne Equipment Research and Test Center，Kunming 650051）

Matrix inversion is a common computationally intensive signal processing algorithm，widely used in sonar detection，radar and other high real-time requirements of digital signal processing.With the maturity of multi-core chip technology，its powerful computing power provides a new matrix solution.In this paper，a matrix inversion method combining Gaussian elimination method with upper and lower triangular matrix decomposition（LU decomposition）is mapped on a heterogeneous multicore reconfigurable system based on NoC.The parallel algorithm is decomposed by combining the parallelism of the system，the memory space and the processing speed of the kernel.The parallel algorithm is decomposed by the parallel algorithm，and the complex matrix inverse of any dimension of 64 dimensions is realized.

matrix inversion，LU decomposition，heterogeneous multicore，algorithm mapping

TP301

10.3969∕j.issn.1672-9730.2017.10.009

Class Number TP301

2017年4月10日，

2017年5月28日

钱庆松，男，硕士，助理工程师，研究方向：水下信号处理。