基于滑模变结构控制的Buck型DC/DC变换器实验研究

陈 龙， 卢 旺

(杭州电子科技大学 电子信息学院， 浙江 杭州 310018)

基于滑模变结构控制的Buck型DC/DC变换器实验研究

陈 龙， 卢 旺

(杭州电子科技大学 电子信息学院， 浙江 杭州 310018)

设计一个滑模变结构控制器以实现变换器良好的输出性能。根据变换器的状态方程，建立系统的数学模型，以指数趋近律作为控制律，得到滑模控制器表达式，采用边界层滑模控制技术减小控制器的抖振，并利用李雅普诺夫函数验证系统的稳定性。Matlab仿真与实验平台实测结果表明,设计的滑模控制器与PID控制器相比具有响应快速、过冲小、鲁棒性强等优点。该实验可加强学生对滑模变结构控制与Buck变换器相关知识的理解，提高学生的实践动手能力以及实验积极性。

Buck变换器； 滑模控制； 指数趋近律； 实验教学

随着技术的不断进步，开关电源得到了广泛的使用，特别是电子、通信、军事等领域[1-2]。DC/DC变换器作为开关电源的重要组成部分，现在对它的研究主要分为2个方向：一是研究出新的拓扑结构来提高变换器的转换效率；二是通过提出新的控制方法和优化算法来改善变换器的转换性能[3-4]。针对DC/DC变换器为非线性系统的特点，传统的线性控制方法如PID控制对其控制效果不理想，所以出现了许多非线性控制方法，滑模变结构控制就是其中之一[5]。滑模变结构控制具体表现为不连续，随着时间的改变具有像开关一样变化的特点[6]。这与DC/DC变换器通过控制开关管的导通与关断来实现电能转换的特性相契合，所以在很多DC/DC变换器的研究中都有滑模变结构控制的应用。本文以Buck变换器为实验研究对象，通过对其进行建模，设计一种合理的三阶(PID型)滑模变结构控制器[7-8]，并对控制器进行仿真和实验，以此来验证控制器设计的合理性。该实验用于教学可以加深学生对滑模变结构控制以及Buck变换器的理解和认识，提高学生的数学建模和实践能力[9]。

1 Buck变换器滑模控制器设计

1.1 Buck变换器系统模型的建立

图1为Buck降压电路拓扑结构，其中，ui为输入电压；VT为功率开关管；VD为续流二极管；L为储能电感；C为滤波电容；R为负载电阻。假设Buck电路工作在完全电感供能模式(CISM)下[10]。

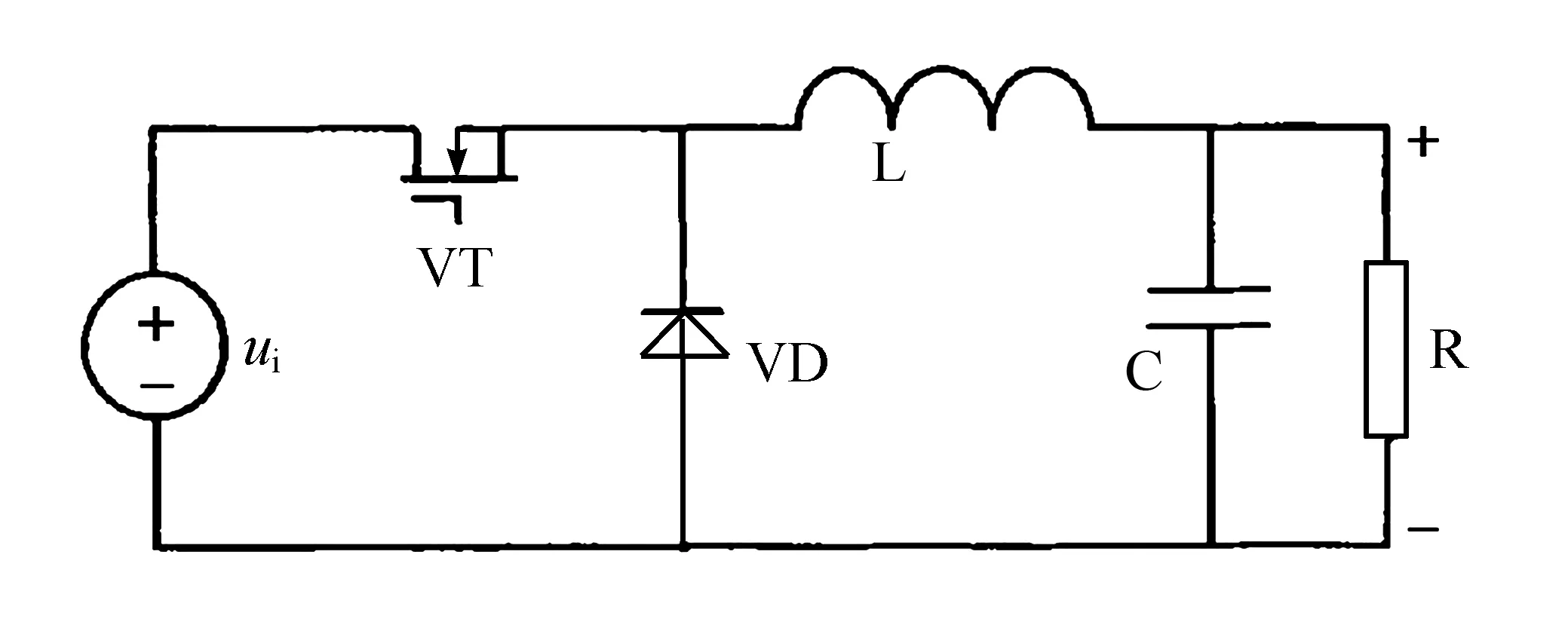
图1 Buck降压电路拓扑结构

对Buck变换器进行电路分析可得系统的状态表达式为

(1)

用矩阵方程表示为

(2)

u为开关函数，定义如下：

(3)

其中：T为开关周期；d=Ton/T=(uo-ui)/uo,d为占空比函数，f=1/T称为开关频率。

1.2 三阶滑模控制器设计

根据系统状态方程设计滑模控制器，将系统的误差定义如下式：

x1=ur-uc

(4)

式中，ur为期望输出电压，uc为滤波电容两端的电压即实际输出电压。

然后分别对x1进行求导和积分，得到x2和x3：

(5)

(6)

再分别对x1，x2和x3进行求导并整理得到：

(7)

把x1、x2和x3当作状态变量，将式(7)写成状态方程形式：

(8)

其中

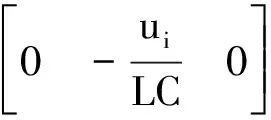
三阶滑模控制器的滑模变量s定义为

(9)

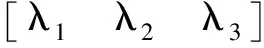
对滑模变量s进行求导并将式(8)代入可得s的一阶导数：

(10)

对滑模控制器选取合适的趋近律，可以提高控制器的鲁棒性和稳定性。本设计采用指数趋近律作为控制律，它具有响应速度快、抖振小等特点[11]。指数趋近律为

(11)

式中sign(s)为符号函数。

根据式(10)和式(11)可得表达式：

λTAx+λTBu+λTC=-ε·sign(s)-ks

(12)

对式(12)进行整理，并用占空比函数d替代开关函数u可得滑模控制器表达式：

(13)

式(13)中含有符号函数如下：

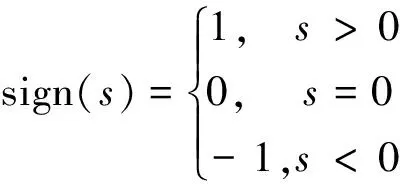
(14)

控制输入过程中可能会发生抖振，所以采用饱和函数sat(s)代替符号函数sign(s)，能够有效地减小抖振，这样就得到了控制器的最终表达式为

(15)

其中，sat(s)的表达式为

(16)

式中，δgt;0，δ为切换面边界层的上限，采用饱和函数对于边界层外的运动点来说起切换作用，而边界层内部的运动点则为线性变化。通过选取合适的δ值，使误差能够收敛到零，从而减小抖振[12]。

1.3 系统稳定性分析

为验证系统是否稳定，利用李雅普诺夫函数验证系统的稳定性[13]。李雅普诺夫能量函数V为

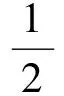
(17)

对V进行求导得：

(18)

当且仅当s=0时，等号成立。

式(18)表明滑模变量s是渐进稳定的，满足李雅普诺夫稳定条件，进而验证了系统是稳定的。

2 软件仿真

设计好滑模变结构控制器后，采用Matlab/Simulink环境[14]对系统进行仿真，Buck变换器参数见表1。

表1 Buck变换器参数

根据式(1)，利用Simulink建立系统仿真模型，对电容电压和电感电流做检测，检验仿真模型是否设计正确，Buck变换器仿真模型见图2。

图2 BucK变换器仿真模型

检测结果如图3所示，从图中可以看出检测结果达到预期效果，说明仿真模型建立正确。

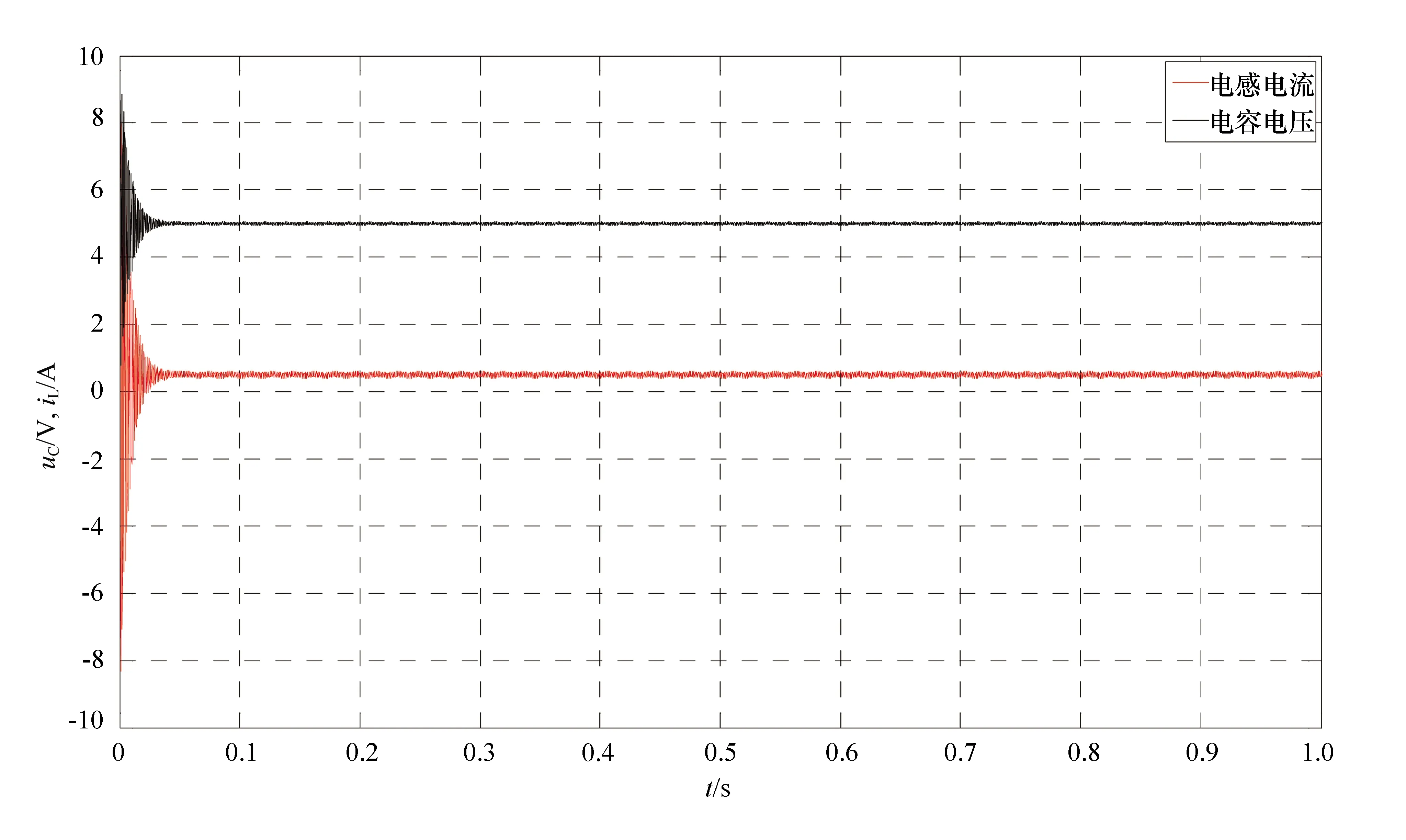
图3 电容电压、电感电流变化曲线

通过Matlab仿真测试所设计控制器的合理性，因为Matlab实际上处理的是离散数据，所以首先需要先将系统离散化，而

(19)

所以，式(8)写成离散形式为

x(k+1)=(AΔ+I)x(k)+BΔu+CΔ

(20)

同理，可得离散指数趋近律(已将符号函数换成饱和函数)：

s(k+1)=(1-Δk)s(k)-ε·sat(s(k))

(21)

由式(20)和式(21)得到离散滑模控制器为

(22)

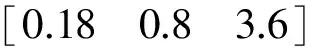
图4 滑模控制与PID控制电压跟踪仿真曲线

表2 滑模和PID控制器电压跟踪仿真比较

从表2中可以发现，在稳态阶段虽然滑模变结构控制的误差比PID控制稍大，但误差都保持在0.5%以内；在启动响应阶段滑模变结构控制的总调节时间(上升时间+调节时间)比PID控制短19 ms，说明滑模控制器具有更快的响应速度，并且变结构控制下的电压超调量明显小于PID控制；在负载扰动阶段滑模变结构控制在有干扰的情况下具有更强的调节能力，调节时间比PID控制短11 ms，以及电压的扰动变化量更小。至此，通过仿真结果表明在同等仿真环境下滑模变结构控制器的性能要优于PID控制器。

3 系统硬件设计

本实验采用飞思卡尔32位微控制K60作为核心控制单元，主要完成PWM信号的输出、控制器算法的实现以及A/D采样。MOS管采用IRF540N，MOS管驱动为IR2013/2104芯片设计的栅极驱动电路(见图5)；采用精密运算放大器TLV2631以及采样电阻来设计制作采样电路。

图5 MOS管驱动电路

根据设计要求和思路对实验平台进行搭建，实物见图6。滑动变阻器用来改变负载的电阻值，J-link仿真器将程序算法下载到单片机上，串口能将Buck变换器上的数据实时地传送给PC的上位机，示波器用来显示波形和检测上位机上的数据是否显示正确。

图6 实验平台实物

4 实验结果及分析

实验平台搭建完成后，对所设计的滑模控制器进行实测，并与PID控制进行性能比较。

4.1 输出电压响应实测

设期望输出电压ur=5 V，图7为滑模控制和PID控制电压响应实测曲线。

图7 滑模控制和PID控制电压响应实测曲线

将图中的数据归纳整理，比较结果见表3。

表3 滑模和PID控制器电压响应实测比较

从表3中可以看出，由于实测是在非理想环境下进行的，所以实测数据会比仿真数据稍大，但大体上与仿真结果保持一致。滑模变结构控制下的调节时间比PID控制约少了22 ms，电压超调量比PID控制低5%，这表明本实验设计的滑模变结构控制器具有更快的响应速度以及更小的过冲量。

4.2 负载扰动实测

为进一步验证所设计的滑模控制器的鲁棒性，对其进行负载扰动实验。图8为在0.8 s时刻将负载从20 Ω调整为10 Ω后，滑模控制和PID控制的电压跟踪实测曲线，负载扰动下两种控制器的输出电压跟踪性能对比见表4。

图8 滑模控制和PID控制负载扰动实测曲线

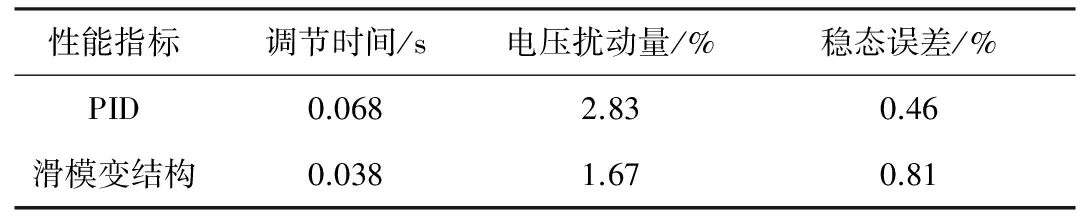
表4 负载扰动下滑模和PID控制器电压跟踪实测比较

从表4可以看出，存在负载扰动的情况下，滑模变结构控制的调节时间比PID控制短约30 ms，并且电压变化量比PID控制低1.1%，表明滑模控制器在负载扰动下有较强的抗干扰能力和良好的调节性能。

5 结语

本实验以Buck变换器为例，设计了一个滑模变结构控制器。仿真与实测表明所设计的滑模控制器相比于传统的PID控制器具有响应速度快、超调量小、调节时间短、抗干扰性能较强等特点。将该实验应用于本科生实验教学，能够达到以下教学目的：了解滑模变结构控制与PID控制相比有哪些优势，滑模变结构控制还可以应用到更多的自动控制领域，例如无人机、两轮平衡车、汽车线控转向系统等；对Buck变换器建立系统状态方程，加深对Buck变换器的理解与认识以及培养数学建模的能力；采用Matlab/Simulink环境对系统进行软件仿真，掌握Matlab软件仿真实验的技巧；通过硬件平台的搭建，熟悉系统硬件设计的思路，锻炼学生的实践动手能力。

References)

[1] 肖永军, 周传璘, 曾庆栋. Buck DC/DC变换器输出电压纹波的仿真研究[J]. 实验技术与管理, 2009, 26(2):87-89.

[2] 牛全民, 张波, 李肇基. 断续导通模式Buck变换器跨周期调制离散解析模型[J]. 中国电机工程学报, 2008, 28(12):32-37.

[3] 袁臣虎. 开关电源DC/DC变换器电路参数及新拓扑研究[D].天津：天津大学, 2011.

[4] 芦守平, 国强, 刁鸣. 基于数字PID的开关电源并联系统实验研究[J]. 实验技术与管理, 2015，32(7):46-48.

[5] Zhou C, Wang Y, Zhang X, et al. Comparative research of digital-PID and sliding mode control strategy for DC/DC converter[C]//Proceedings of the International Conference on Modelling, Identification amp; Control. IEEE, 2014:1-5.

[6] 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3):407-418.

[7] Li H, Ye X. Sliding-mode PID control of DC-DC converter[C]//Industrial Electronics and Applications. IEEE, 2010:730-734.

[8] 郭晨. Boost变换器的PID型滑模控制[J]. 电子科技, 2013, 26(7):51-53.

[9] 王汉萍, 迟洁茹, 于海生,等. 数学建模及竞赛与本科生创新能力的培养[J]. 实验技术与管理, 2009, 26(9):128-130.

[10] 刘树林, 刘健, 钟久明. Buck-Boost变换器的能量传输模式及输出纹波电压分析[J]. 电子学报, 2007, 35(5):838-843.

[11] Song Lizhong, Gong Shuchao, Tian Yingjun. Study of Reaching Law Approach for Discrete-time Variable Structure Control System[C]//Proceeding of 2012 International Conference on Modelling, Identification amp; Control (ICMIC).2012, 206-210.

[12] Utkin V. Sliding Mode Control in Electro-Mechanical Systems[M]. New York，USA：Tayloramp;Francis，2009.

[13] 齐晓慧. “李雅普诺夫稳定性理论”的教学研究[J]. 电力系统及其自动化学报, 2005,17(3):91-94.

[14] 刘金颂, 张庆阳, 苏晓峰,等. Matlab软件在自动控制原理实验中的应用[J]. 实验技术与管理, 2014，31(6):138-140.

Research on experiment of Buck type DC/DC converter based on sliding mode variable structure control

Chen Long， Lu Wang

(School of Electronic Information, Hangzhou Dianzi University, Hangzhou 310018, China)

A sliding mode controller is designed to achieve the good output performance of the converter. According to the state equation of the converter, the mathematical model of the system is established, and the exponential reaching law is used as the control law to obtain the expression of the sliding mode controller. The boundary layer sliding mode control technology is adopted to reduce the chattering of the controller, and the Lyapunov function is used to verify the stability of the system. The measured results of the Matlab simulation and experimental platform show that the designed sliding mode controller has the advantages of fast response, small overshoot, strong robustness, etc., compared with the PID controller. This experiment can strengthen the students’ understanding of the related knowledge about the sliding mode variable structure control and Buck converter, and improve their practical ability and experimental enthusiasm.

Buck converter; sliding mode control; exponential approaching law; experimental teaching

10.16791/j.cnki.sjg.2017.11.018

TN86

A

1002-4956(2017)11-0065-06

2017-04-11修改日期2017-06-15

浙江省2013年高等教育课堂教学改革项目“《数字逻辑电路》课堂教学改革的研究与实践”(kg2013125)；浙江省2015年度高等教育教学改革项目“电子类专业工程创新型人才培养的探索与实践”(jg2015060)

陈龙(1979—)，男，山东宁阳，硕士，副教授，研究方向为嵌入式系统设计与应用、滑模变结构控制、神经网络与机器学习.

E-mailchenlong@hdu.edu.cn