基于气候因素的全球登革热分布的空间模型

◆刘 颖

基于气候因素的全球登革热分布的空间模型

◆刘 颖

登革热是由蚊子作为传播媒介的传染病，致使全球每年2.3亿人收到感染，其中有25000人死亡。本文研究目的是构建全球登革热的空间分布模型，找出影响登革热爆发流行的重要因素。通过以气候因素及人口密度为预测变量，以随机抽样，随机结合系统抽样的方式选择未爆发的地区，与已知的爆发地区组成因变量，使用机械学习中的回归树模型，找出对该疾病流行影响最大的因素。结果表明，对登革热的爆发影响最大的因素是水汽压和人口密度。

登革热；BRT模型；气候因素

登革热是由蚊子作为传播媒介的传染病，主要是通过白纹伊蚊和埃及伊蚊进行传播，多爆发于热带和亚热带地区[1]，致使全球每年2.3亿人受到感染，其中25000人死亡。全球发病率近几十年来迅速增长，约有36亿人，即全球一半以上的人口现在处于危险之中。登革热主要流行在热带和亚热带地区的中心城市，但迅速蔓延到温带地区。基于气候变化情形, 这一增长预计将持续到本世纪末, 特别是在北半球，包括欧洲和中国。在近代欧洲登革热第一次爆发发生在2012年马德拉 - 葡萄牙语群岛。中国已经有登革热疫情的7个地区, 分别是：福建，广东，浙江，台湾，香港，海南，澳门。根据美国疾病预防控制中心报告显示，随着最近几年人口和社会的变化的增强，特别是城市化，全球化，以及迅速增长的国际航空旅游，是登革热发病率上升和地域扩张的主要原因。到目前为止，针对登革热这种流行疾病，既没有抗病毒治疗也没有治疗疫苗，该疾病的主要控制策略是消除传播媒介和个人防护行为。因此，监控，验证和预测人口密度以及登革热病例随着时间的推移在全球范围内的发展是很重要的，尤其是在建模预测未来登革热爆发的概率方面，可以起到指导，控制和提前制定策略的作用。目前，已经有很多研究在关注全球登革热的空间分布[2][3][4][5][6]。

一、研究目的

1.利用BRT模型构建登革热的全球空间分布，并找到对登革热流行影响最大的气候因素。

2.通过比较估计的回归模型的预测变量贡献解释力，研究不同的选择未爆发地区观测值的方法对模型估计值所带来的偏差。

二、数据和方法

（一）数据

我们用来建立回归树模型的数据包括自变量（或预测变量）数据和因变量数据2个部分。自变量数据中有30个气候变量和1个人口密度变量，对于这31个自变量的具体描述见表1。

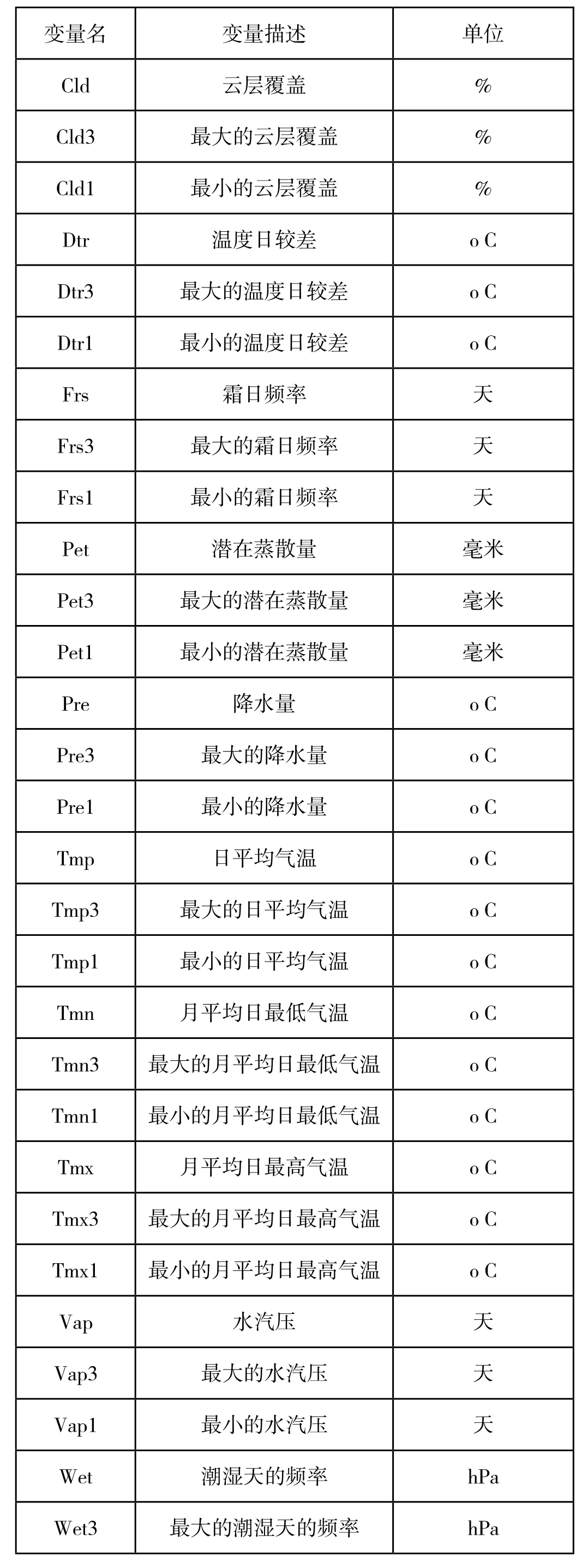
表1. 气候和人口密度变量描述

Wet1 最小的潮湿天的频率 hPa pop 人口密度 人

因变量数据，即登革热数据，是登革热是否爆发的地点观测值。每个观测值都是在以0.5x0.5弧度（arc degree）为基本单位的全球经纬度地理网格上取得的，每个观测值都带有经度和纬度坐标数值[7]。因变量数据共有67420个观测值，其中全球登革热已爆发地区的观测值有1537个，其他地区均为未爆发地区。该数据是由欧洲疾病控制和预防中心European Centre of Disease Control and Prevention (ECDC)提供的。因变量是二项分布，当y=1时表示该地区爆发了登革热，y=0时表示该被观测地区没有爆发登革热。

由于全球登革热确定爆发的地区数量很少，而未确定爆发的地区的数量却非常庞大，所以在对其空间分布进行分析时，通常需要在未爆发地区中随机地抽取与爆发地区数量相同的观测值，同爆发地区一起组成新的数据集，使用回归树模型来对该数据集进行研究分析，从而探究影响登革热爆发的重要因素。

如何在庞大的数据中抽取未爆发地区有多种方法，例如，随机抽样和系统抽样[8]。在本文中展示了3种不同的抽取方式，组成了3个样本数据集，见表2。第一种方式：采用随机的抽样方式在全部未爆发地区中抽取1537个观测值； 第二种抽样方式是随机抽样和系统抽样相结合，先在全部未爆发地区中抽取距离爆发地区小于10 arc degree的观测值， 然后在这些中选的观测值中再进行随机抽取；第三种抽样方式也是随机抽样和系统抽样相结合，但是此次系统抽取的距离缩小到5 arc degree：先在全部未爆发地区中抽取距离爆发地区小于5 arc degree的观测值， 然后在这些中选的观测值中再进行随机抽取。

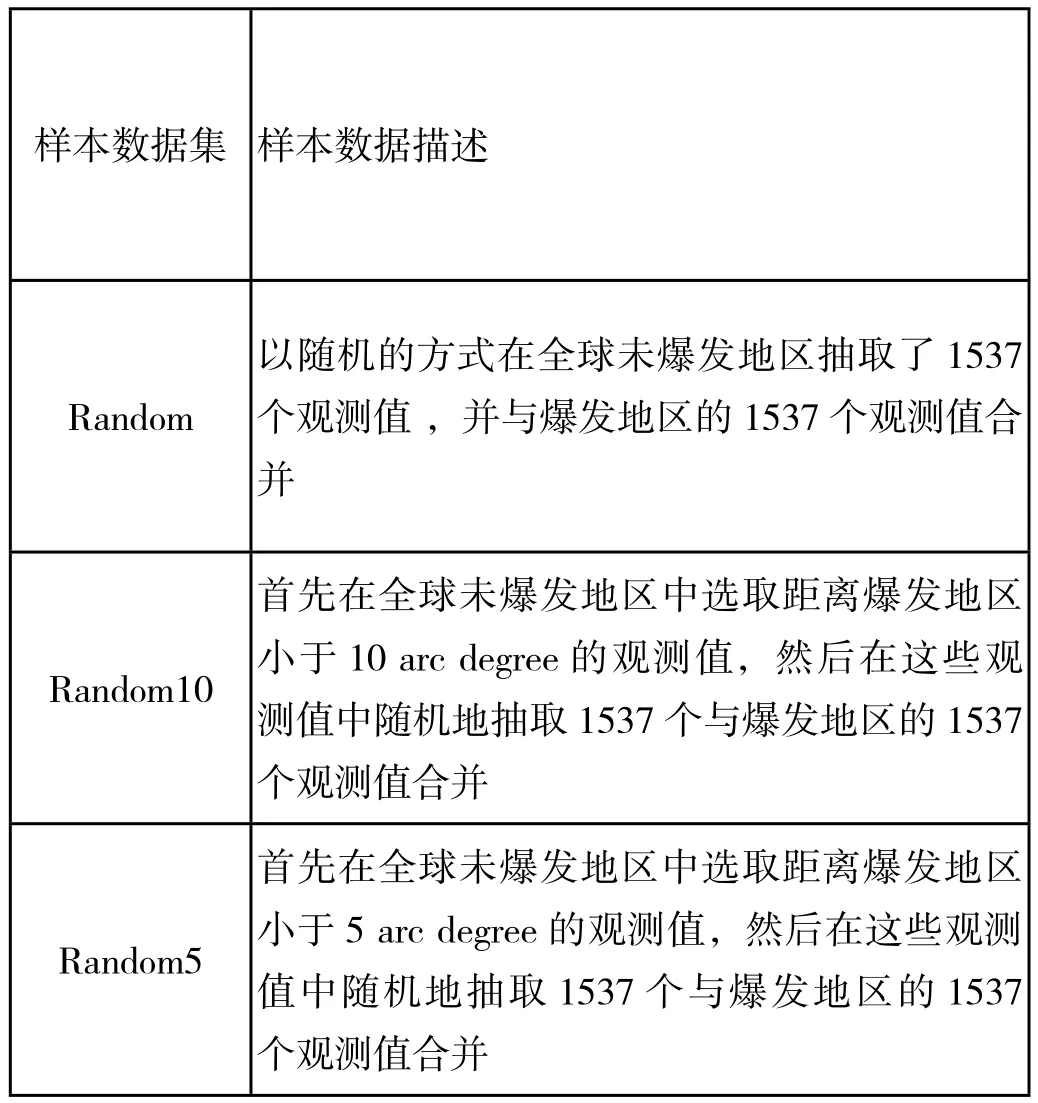
表2. 样本数据集的描述

（二）方法

1.回归树（Boosted regression trees）

回归树模型是机械学习（machine-learning）中的一种，越来越多的空间分布研究开始使用这种分析方法，因为相较于传统的回归模型，回归树模型的预测能力较好，且能够处理非线性问题[9]。如果数据是不易建模的非线性关系，它可以将数据切分成很多个容易构建模型的数据集，然后再利用线性回归技术来对每个切分的数据集建模。如果首次切分之后仍然难以构建线性模型，那就继续切分，直到最后切分的数据集可以建模为止[10]。该模型拟合了每个预测变量对因变量的贡献占全部解释力的百分比，全部预测变量的贡献解释力总和是100%。预测变量的贡献解释力越大，说明它对因变量的影响力越大。

2. Area under the receiver operating characteristic curve（AUC）

AUC是一个评价模型优劣的指标。它是指ROC曲线下方的面积，是一个判断二分类预测模型优劣的标准[9]。它的取值范围是[0，1]，当0.9≤AUC≤1时表示预测模型良好；当0.7≤AUC＜0.9时表示预测模型合理；当0.5≤AUC＜0.7时表示预测模型不是很好[10]。

三、结果

使用R统计软件中的GBM包对3种不同的数据集进行了BRT回归模型分析，并找出了哪些变量对登革热的爆发影响最大；用AUC指标来判断预测模型的拟合优度。通过对不同估计模型的比较，可以发现预测变量的贡献解释力取值是如何根据不同的未爆发地区数据选择方法而变化的。

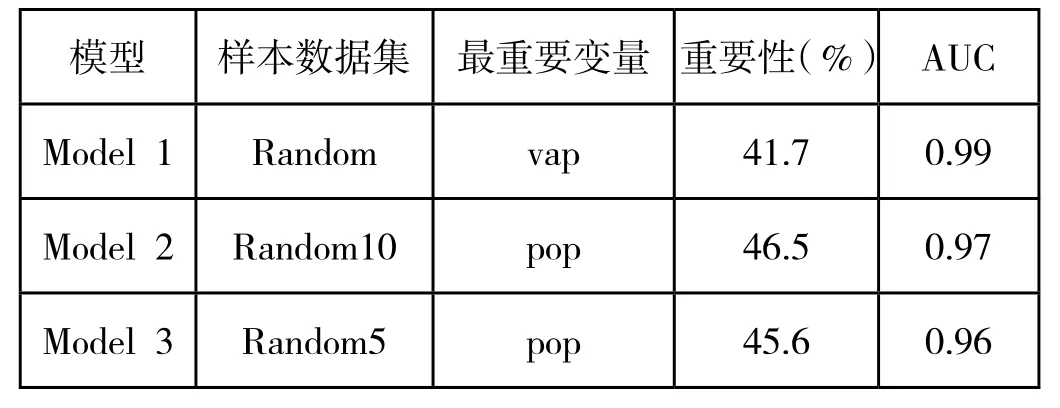
表3. 构建的3个模型的结果展示

Model 1

当使用Random 数据去建立BRT模型时，分析结果显示，影响登革热流行的最主要3个因素是水汽压，它的贡献解释力占比是41.7%；其次是最小的水汽压，占比是20.3%；再次是人口密度，占比是17.2%。该回归树模型的AUC=0.99，表示这个模型的预测性能非常好。

Model 2

当使用Random10数据去构建BRT模型时，影响登革热流行的最重要的前3个因素分别是人口密度，它的贡献解释力占比是46.3%；其次是最小的水汽压，占比是14.7%；再次是最小的月平均日最高气温，占比是6.3%。该回归树模型的 AUC=0.97，表示这个模型的预测性能也非常好。

Model 3

当使用Random5 数据去建立BRT模型时，影响登革热爆发流行的最主要的3个因素是人口密度，它的贡献解释力占比是44.8%；然后是最小的水汽压，占10.6%；最后是占比5.5%的潮湿天的频率。AUC=0.96，表示这个模型的预测性能也很好。

四、结论

（一）影响登革热爆发流行的重要因素

通过建立回归树模型来分析影响登革热爆发流行的因素，拟合出了对于该流行病爆发产生重大影响的气候等因素。本研究发现最重要的影响因素是水汽压和人口密度，其次，温度和湿度也是引起登革热爆发流行的重要原因。所以，当这些因素发生变化的时候，各有关部门要密切关注。因为当气候因素达到了一定条件，例如水汽压大幅变化或温度，湿度适合或上升时，如果人口的流动变化增强，就很有可能会在全球某些地区引起登革热爆发，或导致病情流行范围的扩大。因此，政府和医院的相关单位或部门应该及时有效地监控和预测这些重要的因素，指导，控制和提前指定策略的作用，以防止登革热的爆发，保障人民生命和财产的安全。

（二）不同选择未爆发地区数据的方法带来的差异

随机抽样和系统抽样是在抽取未爆发地区观测值时常见的研究方法。本研究选择了3种不同的方法，同过比较3组不同的数据集拟合出来的模型估计值，发现不同的未爆发地区抽样方法确实对模型的估计值产生显著的影响，并且造成预测性能上的差异。这表示，不同的选择未爆发地区数据的方法会影响预测变量的贡献解释力占比值和预测模型的拟合优度。当使用随机方法在全球范围内抽取未爆发地区数据时，预测模型的拟合度最好；其次是在距离爆发地区小于10 arc degree的观测值中随机地抽取数据；当未爆发地区距离爆发地区越近时，即距离从10 arc degree 缩小到5 arc degree时，拟合优度稍微降低。因此，在抽取选择未爆发地区数据时，要注意采取的抽样方法，因为不同的抽样方法会带来不同的模型拟合结果和预测性能上的差异。

[1]张海林，自登云。虫媒病毒与虫媒病毒病[M]。昆明：云南科学技术出版社 1995.164-174.

[2]Samir Bhatt et al. (2013) The global distribution and burden of dengue. Nature 2013. Doi:10.1038.

[3]Simmons CP, Farrar JJ, Nguyen v V, Wills B. Dengue. NEngl J Med. 2012;366(15):1423-32. Epub 2012/04/13

[4]Astrom C, Rocklov J, Hales S, Beguin A, Louis V, Sauerborn R.Potential Distribution of Dengue Fever Under Scenarios of Climate Change and Economic Development. EcoHealth.

[5]Oliver J. Brady et al. (2012). Refining the global spatial limits of dengue virus transmission by evidence-based consensus. Plos Negl Trop Dis 6(8): e1760. Doi:10.1371/journal.pntd.0001760

[6]Hales S, de Wet N, Maindonald J, Woodward A. Potential effect of population and climate changes on global distribution of denguefever: an empirical model. Lancet. 2002;360(9336):830-4.

[7]http://www.pik-potsdam.de/research/climate-impacts-andvulnerabilitiesch/rd-cross-cutting-activities/isi-mip.

[8]Mary S Wise and Antoine Gusian(2009). Do pseudo-absence selection strategies influence species distribution models and their predictions?BMC Ecology 2009, 9:8 doi: 0. 86/472-6785-9-8

[9]J. Elith et al. A working guide to boosted regression trees.Journal of Animal Ecology 2008, 77, 802-813.

[10]Trevor H, Robert T, Jerome F. The elements of statistical learning.ISBN: 978-0-387-4857-0

[11]J.M. McPherson er al. (2006). Ecologivcal Modelling 192 499-522.

作者毕业于瑞典斯德哥尔摩大学，数理统计系硕士学位。曾在瑞典于默奥大学公共卫生系从事研究助理的工作；现就职于厦门大学嘉庚学院，讲授统计学原理。