随机利率下再保险与最优投资策略的研究

◆于 蕾

随机利率下再保险与最优投资策略的研究

◆于 蕾

对于很多公司为了扩大规模，增强本公司在此行业的竞争力，投资是是一种重要的选择。同时，保险公司为了进一步的降低公司自身的风险，寻找再保险业务也是必由之路。本文主要讨论了保险公司的投资再保险等问题，主要根据随机利率展开研究。随机利率下的最优再保险投资，主要集中在常数波动率的利率模型下对保险公司具有促销预算的研究。随机利息率下投资和再保险相结合的研究在数学处理上难度很大。本文创新性地引入促销预算，使再保险在一种更加合理的形式下给出了问题的解决方案。

再保险；随机利率；最优投资；最优策略

引言

再保险指的是保险公司将拿出它所承担风险和责任中的一部分让其他保险公司来分担，也常常被称作分保，进行了再保险的保险公司称为割让公司。欧洲海上贸易的发展催生了早期的再保险业务，最早的再保险合同可追溯到公元1370年，那正是欧洲海上贸易大发展的时期。中国的再保险市场通过不断扩大开放，吸引越来越多的国际再保险公司进入到中国市场，目前已有法国再保险、通用再保险、慕尼黑再保险、没诺威再保险、劳合社、瑞士再保险等多家国际再保险巨头在中国大陆设立机构。用更理性、更严格的数学方法来研究再保险问题是从20世纪中期后开始的。

一、随机利率下最优再保险－投资策略研究

随机利息率模型是指以瞬时即期利率作为随机状态的一个变量，用一个风险中性测度下的随机过程来描述利息率的变化的数学模型。其最明显的特征是指定当前的即期利率时，但不能知道整个收益率曲线

(一)除了单因素短期利率模型之外，还有多因素短期利率模型。下面是单因素短期利率模型：

Merton模型（1973）将短期利息率描述成

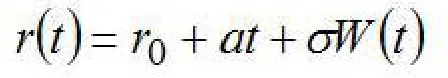
其中常数r0为初始时刻利息率，这里为风险中性概率测度下的一维标准布朗运动。

Ho-Lee模型（1986）将短期利息率描述成

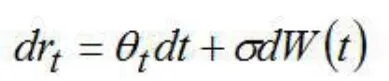
我们使用Ho-Lee（1986）模型来研究利息率的扩散过程，其中现金资产的瞬时利息率为

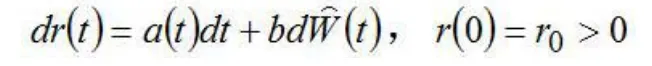
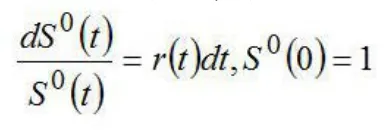
在时间t≥0时的股票市场指数价格可表示为：

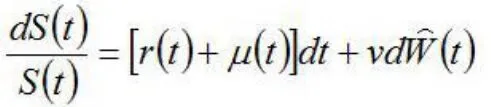
在Ho-Lee模型中，利息率的波动b＞0，而布朗运动可正可负。

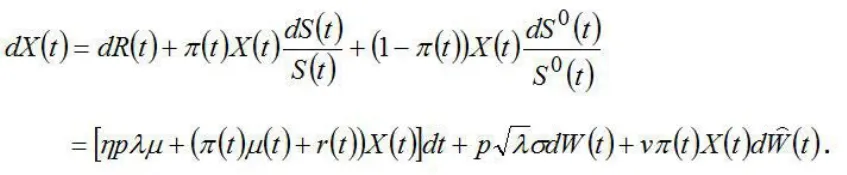
保险公司用财富的固定份额作为预算从每个时刻t收取保费中减掉。

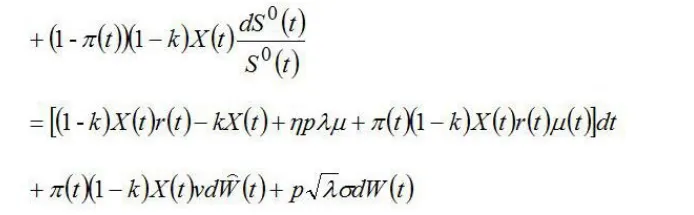
保险公司的目标是让最终财富的期望效用达到最大化。

二、随机利率下具有促销巧算模型的求解

使用期望效用最大化标准，保险公司的目标是最大化终端财富的期望效用，效用函数选用幂效用（常数相对风险厌恶）形式

常数δ∈ (0,1)是保险公司的相对风险厌恶系数。效用函数在数学精算和保险实践中起着重要的作用，对于容许策略对于t时刻的状态定义值函数为

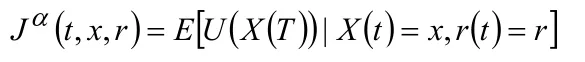
三、总结

风险数学理论开启了保险和再保险领域研究发展的新篇章。在现代社会经济实践中，用促销来吸引客户也是一种重要方式，保险公司也是这样。这种方式既可以让利给客户，又可以吸引更多客户利的双赢举措，是值得关注的。

[1]李哈虹，王春峰，吴启权，随机长短期利率和通货膨胀下的资产配置问题研究，北京理工大学学报（社会科学版），2005，7（6）30-33.

[2]迟国泰：刘冬，杜娟，随机利率下的比例赔付保险模型，运筹与管理，2007，16（3）：114-118.

（作者单位：渤海大学）