基于阈值的快速启动Top-k查询处理算法

江 宇，宋省身，杨岳湘，姜 琨

(1. 西北核技术研究所，陕西 西安 710024；2. 国防科学技术大学 计算机学院，湖南 长沙 410073；3. 国防科学技术大学 信息中心，湖南 长沙 410073；4. 西安交通大学 电信学院，陕西 西安 710049)

基于阈值的快速启动Top-k查询处理算法

江 宇1,2，宋省身2，杨岳湘3，姜 琨4

(1. 西北核技术研究所，陕西 西安 710024；2. 国防科学技术大学 计算机学院，湖南 长沙 410073；3. 国防科学技术大学 信息中心，湖南 长沙 410073；4. 西安交通大学 电信学院，陕西 西安 710049)

Top-k查询是搜索引擎领域广泛应用的技术之一，该算法从海量数据中返回最符合用户需求的前k个结果,在执行时能避免对大部分无关文档的打分处理。Top-k 查询虽然极大提升了查询性能，但其存在的慢启动问题并未得到有效解决。为此，该文首先提取倒排索引的静态Top-k信息，再动态计算针对具体查询词项的初始阈值，在此基础上，结合MaxScore和WAND算法，提出了快速启动的Top-k查询处理算法。实验结果表明，该方法能够有效解决上述问题，具有良好的性能。

Top-k 查询处理；阈值计算；倒排索引

1 引言

对索引文档进行查询排名是信息检索系统最主要的核心任务。目前大型搜索引擎拥有的网页数据已达PB级别且每日处理成千上万的查询请求，使得系统在查询处理过程中耗费大量时间。因此，近年来针对查询处理优化的相关研究得到了商业界和学术界的重点关注。

尽管当前搜索引擎都采用基于各类特征值的排序方法，但对所有候选结果都进行如此复杂的计算显然代价过大。通常，系统会先使用例如BM25等相对简单的检索模型选出小部分可能进入最终结果集的文档，再在后续阶段中引入特征值计算这些文档的分数。在此过程中，Top-k查询处理方法是普遍采用的技术之一。Top-k查询处理又称提前停止或动态剪枝技术，目的是在评估少量候选文档的前提下，试图找出与查询词最相关的前k个结果。Top-k查询处理技术避免了对所有文档的检查打分，极大地提高了搜索引擎的效率。

在前人提出的多种Top-k查询算法中，最为经典的是基于DAAT的MaxScore算法[1]和WAND算法[2]。这两种算法使用跳跃访问倒排链表和部分打分的方式，减少了穷尽遍历算法90%以上的查询开销。自提出以来，研究人员[3-5]主要结合索引结构、文档估分方式和遍历策略等方面对算法进行了改进和优化，但其存在的“慢启动”问题一直没有得到有效解决。“慢启动”问题，即在查询刚开始时，对倒排链表的遍历速度相对较慢，随着查询过程的进行阈值才会逐渐增大，从而加快查询处理速度。

为了解决这个问题，本文围绕初始阈值的设置方法展开研究，在保证算法安全性的前提下，对MaxScore和WAND算法进行相关优化，提出了快速启动的MaxScore算法(rapid start MaxScore, RS-MaxScore)和WAND算法(rapid start WAND, RS-WAND)，并在TREC GOV2数据集上对这两种算法进行了实现和验证。

本文第二节介绍MaxScore和WAND算法的相关工作；第三节介绍快速启动的Top-k查询处理算法RS-MaxScore和RS-WAND；第四节给出本文的相关实验结果及结果分析；第五节总结全文并提出未来工作。

2 相关工作

在搜索引擎和信息检索领域中，根据对倒排链表的遍历方式，大体可分为以下两类查询处理策略： Term-At-A-Time(TAAT)和Document-At-A-Time(DAAT)[6]。TAAT每次只打开一个查询词项对应的倒排链，然后对其进行完整的遍历，并对所有在倒排链中出现的文档的评分进行累加。DAAT则同时打开所有查询词项的倒排链，在并行遍历倒排链的过程中，每次对一个文档进行完整打分。DAAT在大规模数据集的良好性能，使得研究人员提出了多种基于DAAT的 Top-k查询算法。目前，大型搜索引擎普遍采用的是MaxScore和 WAND。

2.1.1 MaxScore

MaxScore算法对每个查询词项的倒排链保留一个指向当前倒排项的指针，同时储存每个倒排链的最大分数，并将链表分为必要和非必要两类。假设当前Top-k的阈值为θ，首先将倒排链按最大分数从大到小排序并对最大分数进行累加，如果累加分数小于θ，则称这些倒排链为非必要链表，反之其他的倒排链称为必要链表。由于只有至少包含一个必要词项的文档才有可能进入Top-k，我们便可以通过对必要链表中的文档进行打分来得到最后结果。从必要链表中文档编号(docID)最小的文档开始作为候选文档，按顺序进行局部打分，即首先计算候选文档在必要链表中的总分数，如果该分数加上非必要链表的最大累加分数仍小于θ，即可终止打分；否则继续累加该文档在非必要链表中的分数，直到得到完整打分或者在累加过程中提前终止。

图1给出了MaxScore算法在查询过程中的例子。图中圆圈表示倒排链的当前指针，圆圈中的数字表示当前指针指向文档的文档号。按照倒排链最大分数排序后，该查询的4个倒排链为{green,blue,red,yellow}，它们的最大分数分别为11、7、4、2，而此时最大分数累加数组的值为20、13、6、2。若当前阈值θ=8，则必要链表T={green,blue}，选取T中文档号最小的文档56为候选文档。首先对blue打分，假设此时有两种情况： ①blue的分数为5。继续对red进行打分，在red中跳过56之前的文档向后查找，结果并未找到56故red分数为0。而此时56号文档的真实分数5加上yellow的最大分数2为7，小于当前阈值，因此不需要再对yellow进行打分，即提前结束打分过程，重新选取下一个候选文档；②blue的分数为6。对red进行同①的处理之后，继续对yellow进行打分，当前指针从7号文档跳跃到56号文档，计算得到的分数与6相加，若大于当前阈值8，则将56号文档插入结果堆中并更新阈值；若小于当前阈值，则重新选择候选文档。

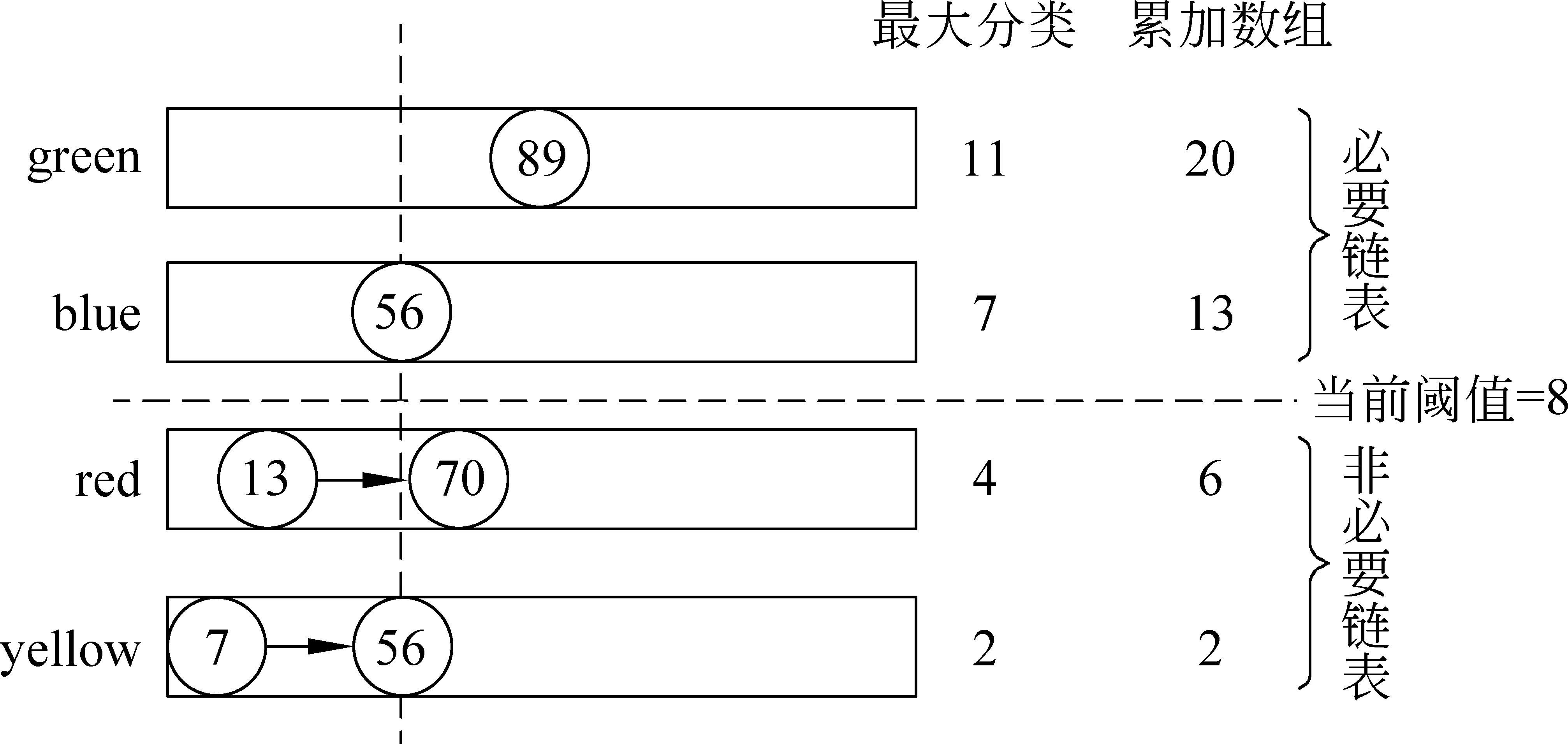
图1 MaxScore算法示例

2.1.2 WAND

WAND算法同样需要预先计算并储存每个倒排链的最大分数。该算法主要有三个步骤： ①选择支点。首先按照各倒排链当前指针指向的docID的升序对倒排链进行排列，再依次对倒排链的最大分数进行累加，当累加分数首次大于或等于当前Top-k的阈值θ时，最后一个参与累加的倒排链对应的词项即为支点词，其当前指针指向的docID为支点ID。②检查对齐。即以docID为准，对所有排列在支点词之前的词项进行对齐——使倒排链的指针移动到docID大于或等于支点ID的倒排项上，如果返回的结果中有docID大于支点ID，则回到第一步对所有倒排链再次排序并重新选择支点词；如果所有返回结果都等于支点ID，则docID为支点ID的文档为候选文档，进行第三步。③对候选文档进行完整打分，用以判断其是否能够真正进入Top-k，然后将所有指针向前移动一步。

图2为WAND算法在查询过程中选择支点的例子。按照当前文档号从小到大排序后，该查询的4个倒排链为{blue,red,green,yellow}，它们的最大分数分别为7、4、11、2。假设当前阈值θ=20，则最大分数累加到green时分数首次大于阈值(7+4+11gt;20)，此时green为支点词，56为支点ID。此时应对blue和red两个倒排链进行对齐，若对齐成功即两个倒排链的当前文档号都为56，则将56号文档视为候选文档，进行完全打分，最后以文档真实分数判断是否能够插入结果堆。若对齐不成功，如图2所示，blue的当前文档号为70，则对倒排链重新排序，变为{red,green,blue,yellow}，重新选择支点词和支点ID。

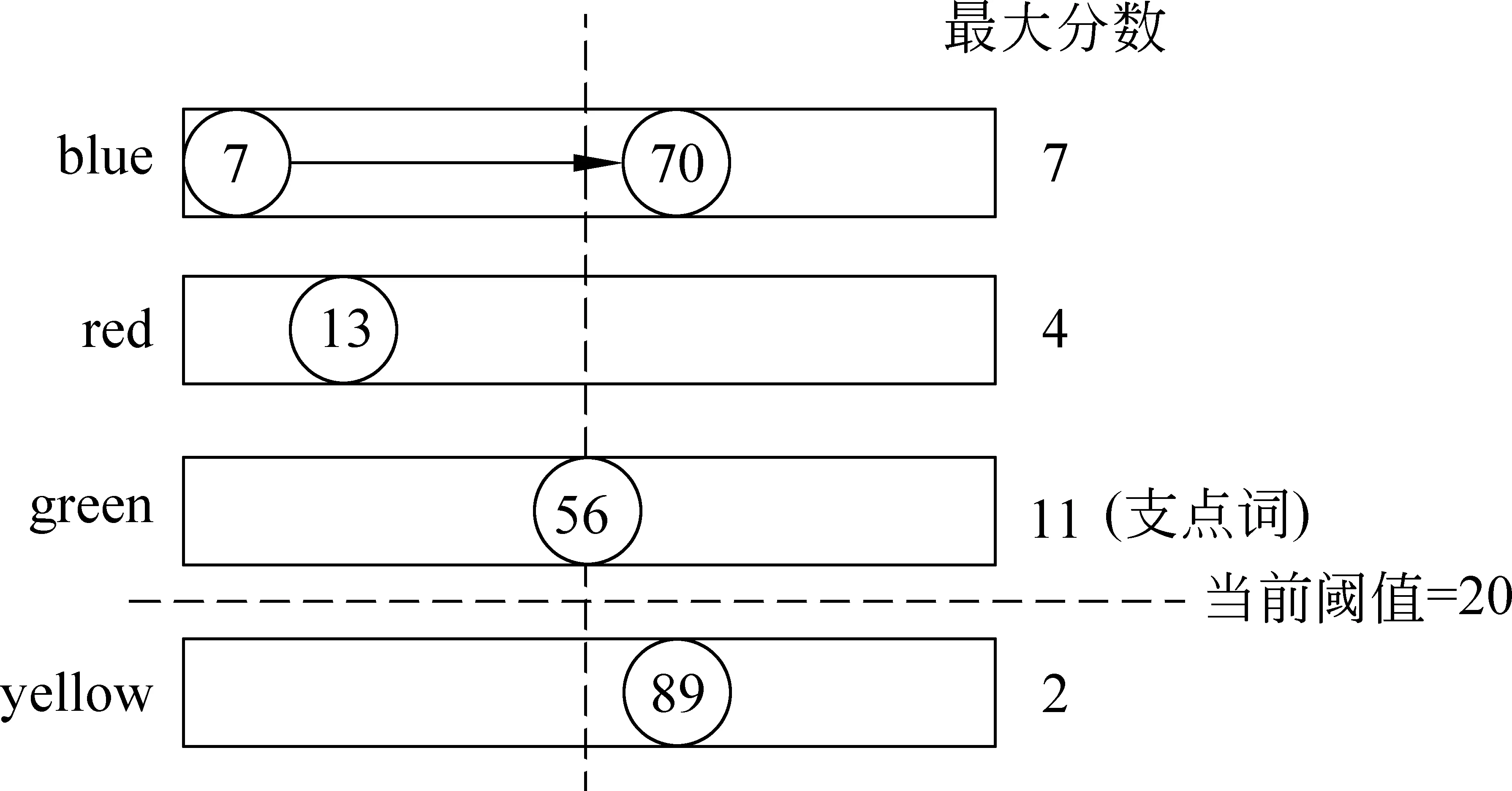
图2 WAND算法示例

从上可知，大体来讲MaxScore和WAND的主要差别是对各倒排链表遍历的顺序不同。而共同之处在于它们都在查询过程中维护一个大小为k的堆来保存当前得分最多的k个文档，并以堆中的最小分数作为阈值。若新的文档分数可能大于阈值，则将其视作候选文档，并进行完全打分，当完全打分后的分数超过阈值，便将相应文档插入堆并更新阈值；反之，则放弃该文档继续遍历倒排链表，直到所有链表均遍历完成。由此，算法的优势在于避免对估分低于阈值的文档进行精确评分，使得查询效率大幅提升。但是，在查询刚开始时，堆中没有文档，初始阈值为0，任何文档都能进入堆中，而这些文档很可能在后面的查询中被相关度更高的文档淘汰。实际上，在开始查询的一段时间里，过低的阈值并没有起到很好的“过滤”作用，使大量相关度小的文档的处理耗费太多时间。随着查询处理的进行，阈值会逐渐变大，查询处理速度将明显变快，这就是上述算法的慢启动问题。由此可见，将初始阈值设置为某个大于0的值可以加快查询处理过程，并且当初始阈值大小等于查询结束时堆的最终阈值(即结果集的最小分数)，将取得最好的加速效果。

Broder等人[2]在提出WAND算法时便对阈值设置进行了讨论，但只对合取查询的非零初始阈值给出了优化方案，但对于应用更广的析取查询没有深入研究；Strohman等人[7]和Rossi等人[8]在分别改进MaxScore和WAND时使用多层索引保存一定比例的高分数文档，计算这些文档分数并使用最小分数作为初始阈值，对提高查询效率有明显效果，但与最优值相比还有一定差距。Ding 和Suel在[9]中将初始阈值的估算作为开放性问题，证明当初始阈值与最终阈值相等时，WAND的查询时间将缩短20%，虽具有指导意义，但并未对计算方法展开讨论。Carvalho等人[10]提出了一种启发式BMW算法，以查询词对应倒排链中排名第k的部分分数作为初始阈值，使查询处理过程有所加快，但这种估算方式依旧不够准确。

结合前人的工作，本文继续对慢启动问题的解决方案进行探讨，提出了一种既保证算法安全性，又更加接近最优值的计算方法，并在TREC GOV2数据集上对该方法进行了实现和验证。

3 快速启动的Top-k查询处理算法

3.1 基本思想

初始阈值的计算涉及两个问题： ①如何保证算法的安全性；②如何设置这个非零值，使慢启动问题能有效解决。Top-k查询算法的安全性，是指使用该算法所得到的结果和使用穷尽查询算法得到的结果是完全相同的，这里的“相同”包括三个方面： 相同的文档、相同的排序和相同的分数。可以看出，上述两个问题是相互矛盾的。从解决慢启动问题的角度看，过小的初始阈值起不到很好的加速效果，故其值应当越大越好。但另一方面，过大的初始阈值将使查询变得不安全。显然，当其值大于结果集的最小分数时，部分本应进入最终结果的文档将会被“丢弃”。实际上，结果集的最小分数RS正是初始阈值的最优解。但这个最优解在查询处理过程完成后才能得到，事先无法进行预测或计算，所以研究人员都致力于让初始阈值尽可能接近该值。

为了更好地估算初始阈值，本文首先在索引阶段提取出每个倒排链分数排名前k的k个倒排项，作为静态信息将其储存在toplist结构当中。对于给定的查询，先对查询词对应倒排链的toplist中的文档进行完全打分，然后把分数按从大到小的顺序进行排列，最后以第k个分数TS作为初始阈值。

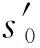
证:令

Sk={sx∈S|sxgt;sk-1,0lt;k≤n},

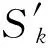
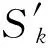
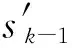
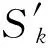
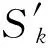
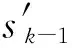
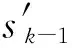
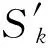
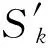
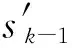
综上，按照上述方法计算的初始阈值不会“丢弃”原本最终排名能够进入前k的文档，保证了算法的安全性。并且当查询词对应倒排链的toplist重合文档数量越多，TS越接近最优解RS；在极端情况下，若toplist文档完全相同，计算得到值等于RS。

3.2 RS-MaxScore和RS-WAND算法

本文将上节所述的初始阈值计算方法与现有两个经典Top-k查询算法MaxScore和 WAND相结合，得到RS-MaxScore算法(伪代码见算法1)和RS-WAND算法(伪代码见算法2)。

算法1RS-MaxScore算法

1.RS-MaxScore(queryTerms[0...q-1] ,k)

2. I[]=getIterators[0...q-1], termID[]=getTermID[0...q-1], numTerms=q,numReqTerms=q; //I为倒排链遍历器

3. initReqScore=calcThreshold (termID[0...q-1]); //计算初始阈值

4. reqScore=initReqScore;

5. 计算最大分数累加数组accScores[0...q-1];

6. loop:whilenumReqTermsgt;0do

7.fori=0;ilt;numReqTerms;i=i+1do

8.ifI[i].doc==lastdocthen

9. 删除I[i], 更新accScores[], numTerms--, numReqTerms--;

10.whilenumReqTermsgt;0andaccScores[numReqTerms-1] lt; reqScoredo

11. numReqTerms--;

12.ifnumReqTerms lt;= 0then

13. break loop;

14. 选择I[0...numReqTerms]中的最小当前文档号为canddoc; //candoc为候选文档号

15. score=0;

16.fori = 0; i lt; numTerms and score + accScores[i] gt;= reqScore; i=i+1do

17.ifigt;=numReqTerms and Ii.skipTo(canddoc) == -1then//跳到大于等于候选文档号

18. 删除I[i], 更新accScores[], numTerms--;

19.elseifIi.doc == canddocthen//计算候选文档分数

20. score +=I[i].score;

21.ifscore lt; reqScorethen

22. continue;

23.else//候选文档分数大于阈值

24. rheap.insert(canddoc, score); //插入结果堆

25.ifrheap.minScore()gt;initReqScorethen

26. reqScore = rheap.minScore(); //当结果堆最小分数大于初始阈值时，更新阈值

27.whilenumReqTerms gt; 0 and accScores[numReqTerms-1] lt; reqScoredo

28. numReqTerms--;

29.returnrheap.result();

算法2RS-WAND算法

1.RS-WAND(queryTerms[0...q-1] ,k)

2. I[]=getIterators[0...q-1], termID[]=getTermID[0...q-1], numTerms=q;

3. initReqScore=calcThreshold (termID[0...q-1]);

4. reqScore=initReqScore;

5. loop:whilenumTermsgt;0do

6. sort(I[0...numTerms-1]);

7. tempScore=0,pivot=0;

8.fori = 0; i lt; numTerms; i=i+1do

9. tempScore+=I[i].maxScore;

10.iftmpaccScoregt;=reqScorethen

11. pivotdoc=I[i].doc;

12.forj = i-1; j gt;=0; j=j-1do

13. I[j].skipTo(pivotdoc);

14.ifI[j].doc() gt; pivotdocthen

15.continueloop;

16. canddoc = pivotdoc;

17. 检查倒排链是否遍历完成，若完成，则删除对应遍历器，更新I[],numTerms--;

18.ifnumTerms==0then

19.break;

20. 对文档进行完全打分，得到文档分数score;

21.ifscore lt; reqScorethen

22.continue;

23.else//候选文档分数大于阈值

24. rheap.insert(canddoc, score); //插入结果堆

25.ifrheap.minScore()gt;initReqScorethen

26. reqScore = rheap.minScore(); //当结果堆最小分数大于初始阈值时，更新阈值

27.returnrheap.result();

从上可知，RS-MaxScore算法和RS-WAND算法与原算法最主要的区别是在进行倒排链遍历前，首先提取查询词ID，再利用toplists中的静态信息调用calcThreshold ()(见算法3)对初始阈值进行计算。当有新结果插入堆后，需要判断堆的最小分数是否大于初始阈值，否则不更新堆的当前阈值。

算法3 calcThreshold (termID[])

4 实验结果与分析

4.1 实验环境

本文使用未压缩的TREC GOV2数据集作为测试集，它包含2 500万个网页，数据规模为426GB。查询语句从Terabyte Track 05 Efficiency查询集中按需求随机选取1 000条，作为实验查询输入。索引采用与文献[11]相类似的多层自索引结构，能够对倒排链进行随机访问。其中，每128个文档号和词频为一个块进行压缩，压缩算法为NewPFD。系统检索模型为Okapi BM25。

系统由Java实现，JDK版本为1.7。测试平台硬件配置为： IntelI CoreI i5处理器，3.20 GHz主频，12 GB内存。

4.2 实验结果与分析

4.2.1 性能指标

表1至表3分别展示了RS-MaxScore与RS-WAND算法在不同k值和查询词长度下，插入堆文档数(Heap inserted)、文档打分次数(Documents scored)、读入磁盘数据块数量(Blocks read)三项主要性能指标，以及与原算法相比取得的性能提升。其中，L表示查询词长度，%I表示性能提升的百分比，H表示每个查询插入堆的平均文档数，D表示每个查询平均打分次数，B表示每个查询平均读入磁盘数据块数量。

从表1可以看出，RS-MaxScore与RS-WAND算法能够有效减少查询处理时插入堆的文档数，这得益于非零初始阈值的“过滤”效果。当k固定时，减少文档数的效果随着L的增大而降低。这是因为L的增大将导致初始阈值计算阶段估算的文档增多，使得到的阈值更加偏离最优解。而当L固定时，减少文档数的效果随着k的增大而提升。这是由于在原算法中，k值越大，查词处理初始阶段进入堆的无效文档越多，使得改进的算法“过滤”的文档相对更多。从表2可以看到，在文档打分次数方面，RS-MaxScore与RS-WAND算法有一定的提升，通过避免对部分文档完全打分加快了查询处理过程。同时应该看到，表3指出在大部分情况下，读入磁盘数据块的数量在算法改进后略微减少，这是因为提出的两种算法仍需对可能进入结果堆的文档进行部分打分评估，从而在读磁盘操作上并不会有明显提升。

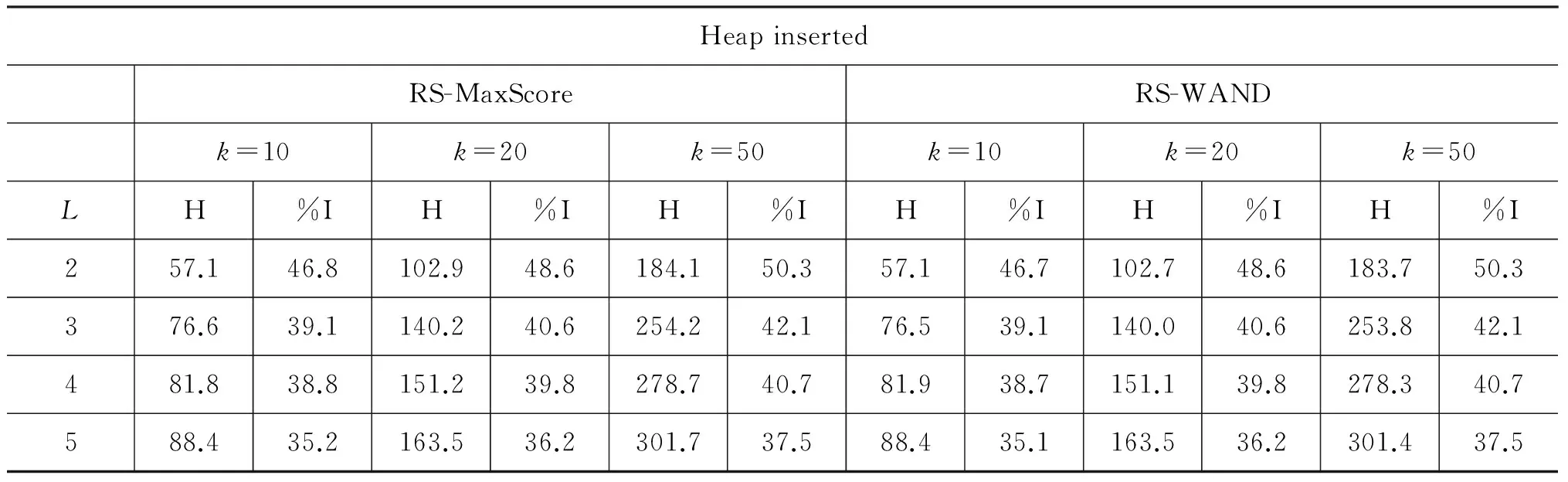
表1 RS-MaxScore与RS-WAND算法的插入堆文档数(H)及其性能提升(%I)

注：L为查询词长度

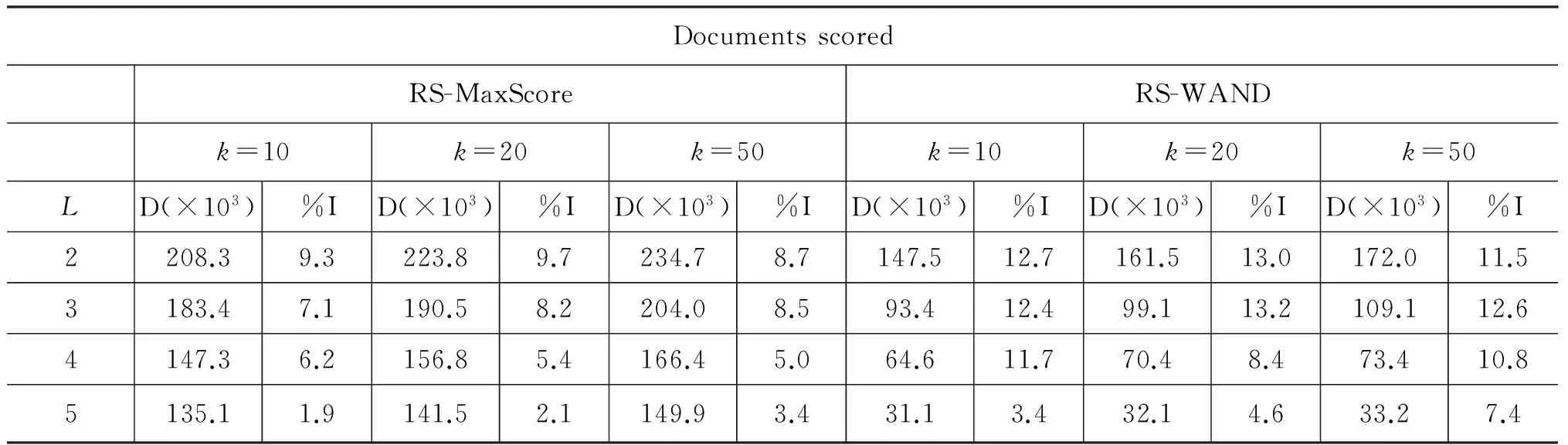
表2 RS-MaxScore与RS-WAND算法的文档打分次数(D)及其性能提升(%I)

注： L为查询词长度

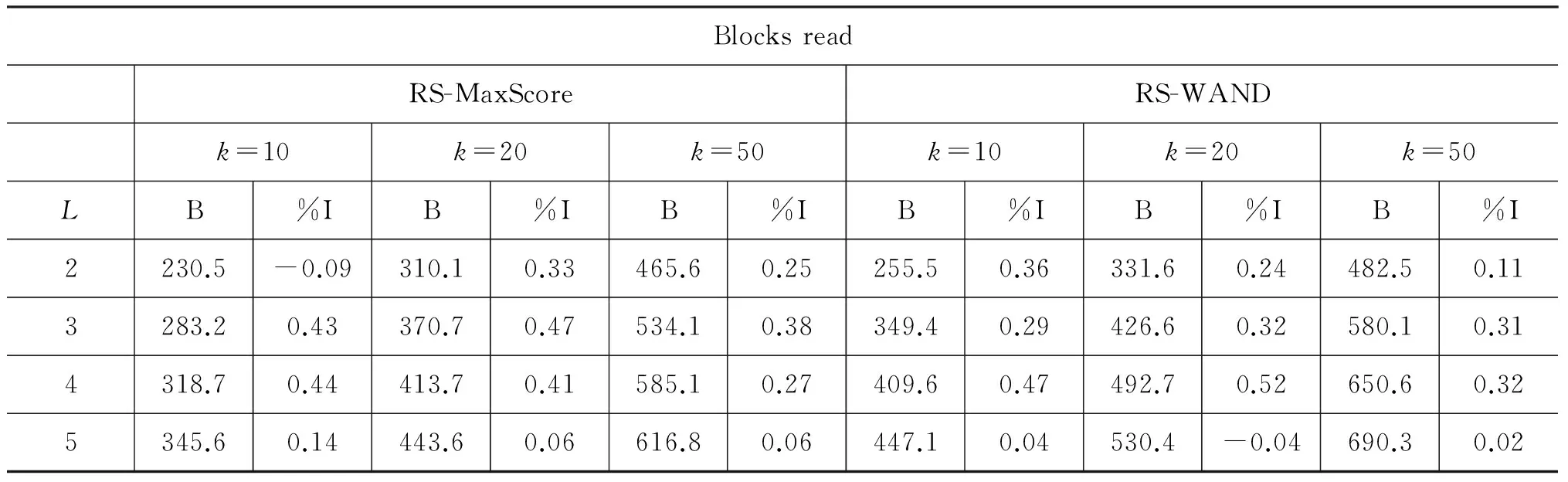
表3 RS-MaxScore与RS-WAND算法读入磁盘数据块的数量(D)及其性能提升(%I)

注：L为查询词长度

4.2.2 不同k值对查询执行时间的影响

图3展示了在不同k值下，MaxScore、RS-MaxScore及RSM-Opt(optimal rapid start MaxScore)三种算法的执行时间，其中查询词长度采用随机选取的方式。RSM-Opt是指初始阈值设置为最优解的快速启动算法，在预处理阶段对固定查询集进行第一次处理，记录每条查询结果集的最小分数后，在正式查询阶段使用记录好的分数作为初始阈值，并使用MaxScore算法对相同查询集进行第二次处理。该算法不具有实际应用意义，但其查询执行时间在理论上为基于阈值计算的改进方式,能够达到的最短时间，具有参照价值。当k=1时，RS-MaxScore与RSM-Opt的初始阈值相同，但由于前者需要对初始阈值进行计算，故查询执行时间略长于后者。当k增大时，三种算法执行时间都随之增长，这是因为返回结果数量的增加意味着结果集文档得分阈值的下降，使得评估文档数增多。在k分别为10、20、50时，RS-MaxScore对原算法的速度提升分别为15.6%、21%、16.7%。

图3 不同k值下MaxScore、RS-MaxScore和RSM-Opt的 平均查询执行时间

图4展示了在不同k值下，WAND、RS-WAND及RSW-Opt(optimal rapid start WAND)三种算法的执行时间。与RSM-Opt相似，RSW-Opt也是初始阈值设置为最优解的快速启动算法，具有参考价值，所不同的是其正式查询阶段使用的是WAND算法。可以看到，与图1相比RS-WAND的时间折线更接近于原算法，说明快速启动的策略对MaxScore来说更加有效，这可能是因为MaxScore在查询过程中并不改变词项链表顺序，非零初始阈值能够有效地划分必要链表和非必要链表，使算法性能提升更高。但即使如此，RS-WAND对原算法的速度提升也在5%～8%之间。

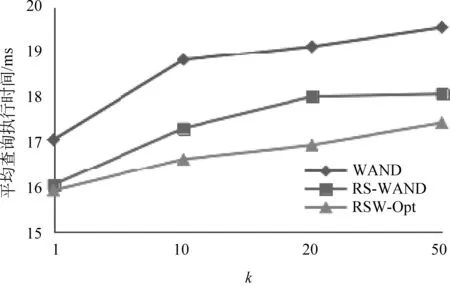
图4 不同k值下WAND、RS-WAND和RSW-Opt的 平均查询执行时间

4.2.3 不同查询词长度对查询执行时间的影响

图5展示了在不同查询词长度下各算法的查询执行时间，其中k=50。从图中可以看出，MaxScore的执行时间低于WAND，且RS-MaxScore的执行时间低于RS-WAND。随着查询词长度L增大，四种算法的执行时间都基本呈增长的趋势。无论L取值多少，RS-MaxScore和RS-WAND的执行时间都比原算法少并都在L=5时取得最佳的效率，分别为20.6%和11.8%。

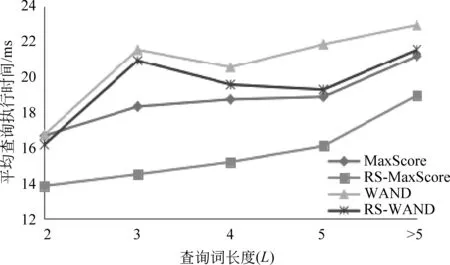
图5 不同查询词长度下各算法的平均查询执行时间

5 结束语

本文针对Top-k查询算法的慢启动问题，对每个查询词倒排链的Top-k文档进行提取，以此为依据对算法的初始阈值进行估算，结合现有的MaxScore和WAND算法，在保证安全性的前提下提出了RS-MaxScore和RS-WAND算法，实验证明，所提方案具有良好的性能。

未来将会在现有工作上进行更多的优化： 进一步探索在估算阈值阶段，合并后的文档数量与原文档数量的比值，估算阈值与最优阈值的比值之间的关系，尝试建立数学模型，从而方便有效地使初始阈值更接近于最优阈值。

[1] Turtle H, Flood J. Query evaluation: strategies andoptimizations[J]. Information Processing amp; Management, 1995, 31(6): 831-850.

[2] Broder A Z, Carmel D,Herscovici M, et al. Efficient query evaluation using a two-level retrieval process[C]// Proceedings of the 12th International Conference on Information and Knowledge Management. ACM, 2003: 426-434.

[3] Moffat A,Zobel J. Self-indexing inverted files for fast text retrieval[J]. ACM Transactions on Information Systems (TOIS), 1996, 14(4): 349-379.

[4] Jonassen S, Bratsberg S E. Efficient compressed inverted index skipping for disjunctive text-queries[M]. Advances in Information Retrieval. Springer Berlin Heidelberg, 2011: 530-542.

[5] Yan H, Ding S,Suel T. Inverted index compression and query processing with optimized document ordering[C]//Proceedings of the 18th International Conference on World Wide Web. ACM, 2009: 401-410.

[6] Ricardo B Y, Berthier R N. Modern information retrieval: the concepts and technology behind search (2nd Edition)[M]. Addision Wesley, 2011, 84: 2.

[7] Strohman T, Turtle H, Croft W B. Optimization strategies for complex queries[C]//Proceedings of the 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2005: 219-225.

[8] Rossi C, de Moura E S,Carvalho A L, et al. Fast document-at-a-time query processing using two-tier indexes[C]//Proceedings of the 36th International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2013: 183-192.

[9] Ding S,Suel T. Faster Top-k document retrieval using block-max indexes[C]//Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval. ACM, 2011: 993-1002.

[10] de Carvalho L L S, de Moura E S, Daoud C M, et al. Heuristics to improve the BMW method and its variants[J]. Journal of Information and Data Management, 2016, 6(3): 178.

[11] Jonassen S, Bratsberg S E. Efficient compressed inverted index skipping for disjunctive text-queries[M]. Advances in Information Retrieval. Springer Berlin Heidelberg, 2011: 530-542.

江宇(1987—)，硕士，工程师，主要研究领域为信息检索。

E-mail： jiangyu1406@163.com

宋省身(1990—)，博士研究生，主要研究领域为信息检索。

E-mail： songxingshen@nudt.edu.cn

杨岳湘(1967—)，博士，研究员，主要研究领域为信息检索。

E-mail： yyx@nudt.edu.cn

RapidStartTop-kQueryBasedonThreshold

JIANG Yu1,2, SONG Xingshen2, YANG Yuexiang3, JIANG Kun4

(1. Northwest Institute of Nuclear Technology, Xi’an, Shaanxi 710024, China；2. College of Computer, National University of Defense Technology, Changsha, Hunan 410073, China；3. Information Center, National University of Defense Technology, Changsha, Hunan 410073, China；4. School of Electronic and Information Engineering,Xi’an Jiaotong University, Xi’an, Shaanxi 710049, China)

Top-k query is a popular technique of search engines, which returns the most relative results for user from massive data. Although Top-k query significantly improves the performance of the system, its slow-start issue has not been effectively resolved. This paper extracts static Top-k information of inverted index and then calculats initial threshold in real time for specific query. On this basis, this paper presents a rapid start algorithm of Top-k query for the current state-of-art methods MaxScore and WAND. Experimental results show that the proposed approach achieves better performance.

Top-k query; threshold-calculation; inverted index

1003-0077(2017)05-0163-08

TP391

A

2016-08-16定稿日期2016-12-26

湖南省自然科学基金(2016JJ2007)