一种用于遥感成像系统的压缩感知编码矩阵设计

张路路 孙权森 刘佶鑫



一种用于遥感成像系统的压缩感知编码矩阵设计

张路路 孙权森 刘佶鑫

（南京理工大学计算机学院，南京 210094）

压缩感知作为突破传统奈奎斯特定理限制的一种信号处理的新途径，近年来受到了诸多研究领域的广泛关注，特别是在遥感成像方面。该理论中，编码矩阵的设计起着非常关键的作用。事实上，原始信号能否被有效压缩，接收端能否将原始信号精确重构，都依赖于编码矩阵设计的优劣。然而，目前常见的编码矩阵普遍不利于硬件的实现，尤其是遥感成像中的采样更是要求计算简单、省电的设备，所以这是影响压缩感知在遥感成像领域推广的主要障碍之一。文章的研究目的是找到一种新的编码矩阵，既有良好的压缩感知采样性能，又有利于针对遥感应用的硬件实现和降低硬件成本。鉴于分块压缩感知在重构时的优势即提升重构速度和品质，提出了基于分块的二级尺度编码矩阵设计，即在第一次分块的基础上再次分块，并以此基础设置编码矩阵。通过实验模拟实际的硬件采样过程，分析所设计编码矩阵的不足之处，并对其进一步优化，使得所搭建的硬件成像平台中对图像采样的数据可以在终端进行高品质的重构。

压缩感知 编码矩阵 多尺度 重构 遥感成像系统

0 引言

传统遥感技术采样过程为避免信号失真，其采样频率受到香农采样定理的严格限制，即采样频率必须达到信号带宽的两倍以上才能精确重构信号。此外，随着人们对遥感信息需求的海量化，遥感技术中的采样、传输和压缩等过程面对巨大压力。在传统遥感技术中主要存在三个方面问题需要解决：1）遥感器研制的高成本；2）数据压缩和传输的难题；3）天、地遥感数据处理的不对称性，即传统遥感压缩技术复杂，而解码过程则比较简单。这三个问题都说明了目前遥感成像需要降低存储和传输成本，而要实现这个目的就要对这些大量的冗余数据进行简单而又易用的压缩。然而现代遥感成像通常使用 DCT （jpeg）或者Wavelet（jpeg2000）编码达到压缩的目的。由于变换域的数据只有一小部分具有很大的值，因此可以通过阈值方法过滤掉那些非常小的值，然而这个方法存在一个明显的缺点：阈值会使所获得的大量数据被舍弃，从而造成时间上的浪费。

文献[1]提出了压缩感知理论。压缩感知（CS）指对原始信号进行非自适应线性投影得到观测值，然后利用稀疏性的先验知识，通过求解一个优化问题，从已知的少量投影值中以高概率重构出原始信号。所以，在遥感成像中的观测端可采用线性编码，终端采用非线性解码，这正与如今两者相应的科技发展相一致。从而解决了遥感成像中的2）、3）两个问题。如何设计实用的编码矩阵正是对这两个问题的解决关键。

编码矩阵[2]作为压缩感知理论中重要的研究方向之一，受到了很多学者的重视。人们希望编码矩阵的生成不依赖于信号本身，同时基于该矩阵的投影结果又能承载原始信号的几乎全部信息。文献[3]首先提出了随机编码矩阵；文献[4-5]中给出了这些随机观测矩阵满足等距约束性（RIP）条件的详细证明。在随机编码的基础上，很多学者又给出了进一步的研究，主要分为两个方向：一是对已有编码矩阵的优化，如文献[6-7]指出利用QR分解优化编码矩阵；文献[8]提出了基于编码矩阵的行向量正交化的改进方法；另一个方向是构造新的编码矩阵，如文献[9]将混沌序列引入压缩传感；文献[10]则给出了稀疏投影编码矩阵和非常稀疏投影编码矩阵；文献[11]将确定性编码矩阵引入压缩传感，为压缩感知中编码矩阵构造打开一个新的方向。

目前遥感成像正在逐渐向高分辨率和大视场角趋势发展,这给遥感成像中的硬件带来了更大的挑战。所以，针对这个背景我们需要有一个可在硬件当中易于实现的编码矩阵对拍摄的遥感图像进行压缩，根据分块压缩感知重构[12]和多项式确定性测量矩阵[13]，提出多尺度编码矩阵的设计。

1 基本理论介绍

1.1 压缩感知理论

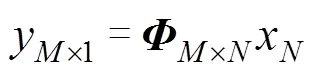
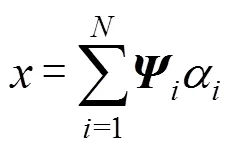
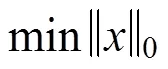
1.2 常见的编码矩阵及存在问题

为了保证能够从观测值准确重构信号，需要满足如下条件：观测矩阵与稀疏基矩阵的乘积满足RIP性质[3-4]。其具体表达如下式：

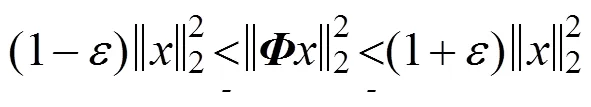
这个性质保证了观测矩阵不会把两个不同的稀疏信号映射到同一个集合中（保证原空间到稀疏空间的一一映射关系），这就要求从观测矩阵中抽取的每个列向量构成的矩阵是非奇异的。

目前已经存在的编码矩阵可分为两大类：随机编码矩阵与确定性编码矩阵。

常见的随机编码矩阵包括：高斯随机编码矩阵，其内的元素都满足高斯分布；二值随机编码矩阵[16]；伯努利随机编码矩阵；部分哈达玛编码矩阵；稀疏编码矩阵等。高斯随机矩阵虽然生成简单但在实际应用中（特别是数字成像领域）中很难设计出可行的硬件系统或电子元器件。二值随机矩阵弥补了高斯矩阵的缺点，在单像素成像[17]的研究中，使用DMD芯片可以很容易的生成二值随机矩阵。但是这类的矩阵有一个很明显的缺点：元素都是满足某种分布，随机性比较高。

基于上述随机矩阵的缺点，文献[11]提出通过有限域中多项式的取值来构造矩阵。重构二维图像时，选用合适重构算法，多项式确定性测量矩阵重构效果优于高斯随机矩阵，但此类矩阵的缺陷在于：矩阵大小受限制，不适宜广泛应用。基于膨胀图的确定性测量矩阵受到广泛关注[18],但此类算法的缺陷在于很难找到确定结构的膨胀图。托普利兹观测矩阵与哈达玛观测矩阵中的值只能取正负1，从这些确定性矩阵来看，虽然具有一定的实用性，但是大多都只能是用于全局编码，在硬件平台上都不易于实现。

2 基于多尺度的编码矩阵设计

根据上一节所述常见编码矩阵的缺点，提出一个多尺度编码矩阵设计方法。所谓多尺度即将事物属性或系统行为在尺度上的划分，多尺度机制的理论基础来自于文献[19]提出的多尺度透镜组，其优势在于通过不同尺度光学系统的组合可以实现大视场角的高分辨率成像，这符合目前遥感成像的发展要求,并且有利于图像压缩与重构的GPU并行化[20]大幅度提升运算速度。本文所提的多尺度即对图像进行两次分块，其中第一次分块为一级尺度划分，在第一次分块的基础上进行第二次分块即二级尺度。图1中的多尺度采样如图1所示：如图1所示的1、2、3等设定为一级尺度划分，1、2、3为一级观测值，作为批量式重构[13]的基础；11、22、33等设定为二级尺度划分，11、22、33为二级观测值，作为编码矩阵设计的基础。假设原始图像为×，则本文的多尺度编码分为以下几步：

图1 基于两级尺度的采样

1）初始化×大小的01随机矩阵；

2）×随机矩阵划分成若干个×大小的一级尺度矩阵；

3）×的一级尺度矩阵划分成若干个×的二级尺度矩阵，对×矩阵编码；

4）在局部编码的基础之上对×大小的矩阵调整。

分块压缩[12]感知比传统压缩感知节省存储空间和提升运算速度。因此，对编码矩阵进行分块，即一级尺度划分，有利于终端的批量式重构。为了能够更好的有利于硬件的实施，在一级尺度内再次划分更小的尺度，在二级尺度内设计编码矩阵。为了说明二级尺度的编码矩阵，需要设定下采样的采样率：

理论上，假设信号是稀疏的，则其观测次数与信号长度需满足如下关系：

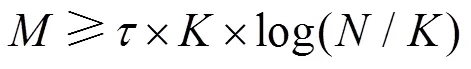
（a）城市 （b）掩模板 （c）采样图

（a）City （b）Mask （c）Sampling image

图2 基于真实图像的二级采样

Fig.2 Sampling based on real image

图2中的小的红色矩形框标注的就是二级尺度的局部编码，每一小红色矩形框之间的关系决定了二级尺度的全局编码。由上述分析得到，编码矩阵设计的条件是：

1）获取二级尺度矩阵内×个像素值中的个像素值，1<<×；

2）二级尺度内的像素值满足0，1分布；

3）二级尺度内像素的透光位置之间的关系；

4）二级尺度间像素的透光位置之间的关系。

根据编码矩阵设计的条件4），二级尺度之间的排列组合情况如下式所示：

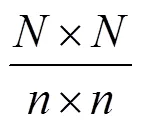
式中为二级尺度的个数，大小的矩阵共有种二级尺度之间的排列组合。本文以二级尺度作为编码的基本单位，以一级尺度作为重构的基本单元。从一级尺度的角度看编码矩阵，每个二级尺度可看作单独的一个像素点，需要满足二级尺度排列后的连续透光规则，这个编码过程称为全局编码。

结合上述分析，编码步骤如下：

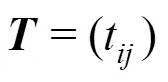
3）设置一个大小的矩阵，其内的值全为1，令该矩阵对造成编码矩阵设计的条件。

4）情况的任意一个编码矩阵中的×矩阵进行异或操作，则调整后的矩阵为本文所设计的全局最优编码矩阵。

测量矩阵和稀疏矩阵要满足不相干性和受限等距性，由于受限等距性的复杂度高，文献[22]指出若矩阵与稀疏基满足不相干性即矩阵与稀疏基互相不能线性表示，则该矩阵可用作编码矩阵。所以本文依据该性质证明所提矩阵的可行性，不相干性可表示如下：

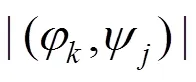
3 实验

本次实验的软件环境为matlab r2012a，选用大小为700×700像素的城市、农田、山脉三种地物类型。采样率设置为0.25，重构算法采用OMP，稀疏基采用DCT，一级尺度矩阵大小为16×16像素，二级尺度矩阵大小为2×2像素，选取2×2像素中的两个像素值，选择高斯矩阵（Gaosi）、伯努利矩阵（Bernoulli）、和哈达玛矩阵（Hadamard）作为实验对比对象。由第二章节可知，对2×2矩阵按列排列成列向量，透光位置与未透光位置有图3所示的6种情况（白色圆圈代表编码矩阵中的透光位置，黑色圆圈代表不透光位置）：

图3 2×2块内排列

二级尺度之间则会出现如图4所示的需要调整的4种情况：

图4 2×2块间排列

为了更准确的反映实验结果，采用一个指标：可辨识度。图5所示为靶标图。图5（c）能清晰的看到图中所示位置的靶标，从视觉的角度观察，重构的效果很好。

（a）原图 （b）采样图 （c）重构图

图6中横坐标的“0”与“1”用“0”表示图3、4中的实心黑色圆圈，“1”表示空白圆圈。1010、1001、0101、1100、0011、0110称为局部编码，“模块为0”表示局部编码组合在一起出现4个像素为0，由图6可以看出局部编码中的透光像素不连续的时候效果比现有的方法差很多。针对编码矩阵设计的条件3）（参见本文第2节）进行优化后的效果远远好于现有的编码矩阵。对编码矩阵设计的条件4）（参见本文第2节）的优化分为两种情况：一是图4第一种“模块为0”的时候，对其进行优化后的结果如图中的“优化1”所示；二是对模块间连续像素为0的情况进行优化，如图4后三种情况，在此基础上加入全局因素，使得局部编码保持连续像素透光之外，模块与模块间减少连续为0的情况，由“优化2”可知效果有所提升。本文选取城市地物的重构图像比较重构图像的细节，如图7所示：

图6 不同地物在不同编码矩阵下的PSNR值

（a）高斯 （c）哈达玛 （e）伯努利

（a）Gauss （c）Hadamard （e）Bernoulli

（b）1010 （d）优化1 （f）优化2

图7（b）表示局部编码透光像素点不连续的情况，对应图6中的1010情况，7（d）图中的优化1表示子模块透光像素点连续的情况，对应图7中的0110情况，7（f）图中的优化2表示在优化1的情况下，子模块间不出现连续透光像素的情况。由图6和7可知，本文最终生成的编码矩阵的采样效果优于常见的编码矩阵。

4 结束语

本文分析了目前常用矩阵在应用中的局限性，为了能够在所搭建的硬件平台中设计出易于制作且有高效率的硬件采样平台，结合确定性观测矩阵与分块压缩感知重构提出了多尺度压缩感知采样矩阵。多尺度的划分不仅为掩模板的设计带来了便利，而且在终端也能够快速且精确的重构原始遥感图像。本文讨论了局部编码的几种情况并且加入全局因素进行优化，使得各模块之间的像素信息能够尽可能保留下来。根据靶标图来看，无论是软件仿真采样后的重构效果还是真实采样后的重构效果，从视觉上来看，都满足实际应用的需求。由于遥感图像的特殊性，我们采取了三种地物类型加以验证，从实验数据上来看，只考虑局部编码则只有像素相邻时才有好的效果，最后进行全局优化后，效果又有显著的提升。但是，本文所做的仿真实验没有考虑实际采样中光照和硬件平台的局限性，在编码矩阵中再加入一些约束条件逼近真实的采样是接下来的研究重点。

[1] BARANIUK R G. Compressed Sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121.

[2] CANDES E J, WAKIN M B. An Introduction to Compressive Sampling[J]. IEEE Signal Process. Mag., 2008, 25(2): 21-30.

[3] CANDES Emmanuel, TAO Terence. Near Optimal Signal Recovery from Random[J]. Projections: Universal Encoding Strategies. IEEE Trans. Inf. Theory, 2006, 52(12): 5406-5425.

[4] BARANIUK R, DAVENPORT M, DEBORE R, et al. A simple Proof of the Restricted Isometry Property for Random Matrices[J]. Constructive Approximation, 2008, 28(3): 253-263.

[5] GUREVICH S, HADANI R. Incoherent Dictionaries and the Statistical Restricted Isometry Property[J]. Eprint Arxiv, 1997: 175-181.

[6] 傅迎华. 可压缩传感重建算法与QR分解[J]. 计算机应用, 2008, 25(9): 2300-2306. FU Yinghua. Compressible Sensing Reconstruction Algorithm and QR Decomposition[J].Computer Application, 2008, 25(9): 2300-2306. (in Chinese)

[7] SZAREK S J. Condition Number of Random Matrices[J]. Journal of Complexity, 1991, 7(2): 131-149.

[8] 李小波. 基于压缩感知的测量矩阵研究[D]. 北京交通大学, 2010. LI Xiaobo. Research on Measurement Matrix Based on Compressive Sensing[D]. Beijing:Beijing Jiaotong University, 2010. (in Chinese)

[9] 顾国生, 战荫伟. 一种混沌序列在压缩感知观测矩阵中的应用[C]. 全国图象图形学学术会议, 2010. GU Guosheng, ZHAN Yinwei. Application of a Chaotic Sequence in the Compressed Sensing Observation Matrix[C]// National Conference on Graphics and Graphics, 2010: 111-114. (in Chinese)

[10] 方红, 章权兵. 基于亚高斯随机投影的图像重建方法[J]. 计算机研究与发展, 2008, 45(8): 1402-1407. FANG Hong, ZHANG Quanbing. A Method of Image Reconstruction Based on Subgaussian Random Projection[J]. Journal of Computer Research and Development, 2008, 45(8): 1402-1407. (in Chinese)

[11] NIE Y, YU X L, YANG Z X. Deterministic Construction of Compressed Sensing Matrices[J]. International Journal of Grid and Pistributed Comprting, 2016(9): 397-406.

[12] LU G. Block Compressed Sensing of Natural Images[C]// International Conference on Digital Signal Proc, 2007: 403-406.

[13] DONHO D. For Most Large Underdetermined Systems of Linear Equations the Minimal L1-norm Solution is also the Sparsest Solution[J]. Communications on Pure & Applied Mathematics, 2006, 59(6): 797-829.

[14] ZHANG Z, RAO B D. Extension of SBL Algorithms for the Recovery of Block Sparse Signals with Intra-block Correlation[J]. IEEE Transactions on Signal Processing, 2013, 61(8): 2009-2015.

[15] NEEDELL D, TROPP J A. CoSaMP: Iterative Signal Recovery from Imcomplete and Inaccurate Samples[J]. Applied & Computational Harmonic Analysis, 2008, 26(3): 301-321.

[16] CANDES E J. Compressive Sampling[J]. Marta Sanz Solé, 2006, 17(2): 1433-1452.

[17] DUARTE M F, DAVENPORT M A, TAKHARAKHAR D, et al. Single-pixel Imaging via Compressive Sampling[J]. IEEE Signal Processing Mag, 2008, 25(2): 83-91.

[18] JAFARPOUR S, XU W, HASSIBI B, et al. Efficient and Robust Compressed Sensing Using Optimized Expander graphs[J]. IEEE Transactions on Information Theory, 2009, 55(9): 4299-4308.

[19] BRADY D J, GEHM M E, STACK R A, et al. Multiscale Gigapixel Photography[J]. Nature, 2012, 486(7403): 386-389.

[20] 柳家福, 贺金平. 基于GPU 的高光谱遥感主成分分析并行优化. 航天返回与遥感[J]. 2014, 35(6): 99-106. LIU Jiafu, HE Jinping. Parallel Optimization of Principal Component Analysis of Hyperspectral Remote Sensing Based on GPU[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(6): 99-106. (in Chinese)

[21] 刘吉鑫, 孙权森. 分形压缩感知在数字成像中的应用[J]. 测绘学报, 2013(6): 846-852. LIU Jixin, SUN Quansen. Applied Research of Fractal Compressed Sensing in Digital Imaging[J]. Acta Geodaetica et Cartographica Sinica, 2013(6): 846-852. (in Chinese)

[22] RAUHUT H, SCHNASS K, VANDERGHEYNST P. Compressed Sensing and Redundant Dictionaries[J]. IEEE Transactions on Information Theory, 2008, 54(5): 2210-2219.

（编辑：刘颖）

Design of Compressed Sensing Coding Matrix in Remote Sensing Imaging System

ZHANG Lulu SUN Quansen LIU Jixin

（Nanjing University of Science and Technology, Computer Institute, Nanjing 210094, China）

As a new way to break through the traditional Nyquist signal acquisition theorem, compressed sensing has received widespread attention in recent years, especial in remote sense imaging. The design of the observation matrix in compressed sensing plays a very important role. In fact, whether the original signal can be effectively compressed and then be accurately reconstructed in the receiving device, largely depends onthe quality ofthe observation matrix. However, the observation matrix at present has a serious drawback: it is hard to be implemented; especially in remote sensing image sampling a simple and power-saving equipment is indispensable. The purpose of this study is to find a matrix with good performance and also easy to be implemented. In view of the advantages of the sub block compression perception in the reconstruction speed and quality, the two-level scale encoding matrix design was proposed based on the sub blocks, that is, the first block was divided, and then the encoding matrix was set. Through the simulation of optical mask sampling process, the design of the encoding matrix was analyzed and optimized and then the origin image was reconstructed with high quality in the terminal device.

compressed sensing; encoding matrix; multi-scale; image reconstruction; remote sense imaging system

TN919.81

A

1009-8518(2017)05-0068-08

10.3969/j.issn.1009-8518.2017.05.009

张路路，男，1989生，南京理工大学计算机科学与工程学院硕士研究生，研究方向为遥感图像处理与应用。E-mail：870225800@qq.com。

2017-02-07

国家自然科学基金（61273251）