前缘切口参数对大型冲压式翼伞的性能影响分析
黄炎 张红英 杨璐瑜 陈建平 童明波
前缘切口参数对大型冲压式翼伞的性能影响分析
黄炎 张红英 杨璐瑜 陈建平 童明波
(南京航空航天大学飞行器先进设计技术国防重点学科实验室,南京 210016)
影响冲压式翼伞气动性能的主要参数除翼型结构参数外,还有翼伞前缘切口角度和前缘切口长度。为了更准确地找到冲压式翼伞前缘切口参数适用的工程应用范围,文章以某大型冲压式翼伞的基础翼型剖面为研究基础,通过改变前缘切口角度和前缘切口长度这两项重要参数,得到四种具有代表性的前缘切口参数的翼型剖面,并采用数值计算方法对其气动性能进行分析。研究表明:负攻角时,上翼面的压力梯度随前缘切口角度的增大而增大,而下翼面的压力梯度随前缘切口角度的增大而减小;正攻角时,前缘切口角度对上、下翼面的压力梯度没有太大影响;同时,随着前缘切口角度的增加,翼型最大升阻比也增大,但是会有一个临界值,而前缘切口参数对翼型俯仰力矩系数的影响并不大。文章的研究结果对翼伞的设计优化有一定的参考意义。
前缘切口角度 前缘切口长度 气动性能优化分析 冲压式翼伞
0 引言
冲压式翼伞作为一种可控的气动减速装置,在空间探测与航天返回着陆、精确空降空投、航天器回收等领域都有广泛的应用。
在大部分飞行时间中,翼伞均处于稳定滑行阶段,这个阶段翼伞的气动性能对于翼伞的总体设计尤为重要。翼伞基本翼型截面在其前缘有切口,空气能够通过切口进入翼伞,使织物撑起气动外形,而切口的位置和尺寸对翼伞系统的性能有着重要影响。太小的前缘切口会导致翼伞充气时间过长,甚至失败。一个非常大的切口会使气动性能不佳,而且在更短的充气时间内,翼伞会受到很大的拉力影响。因此前缘切口的理想尺寸是翼伞设计的关键要素[1-4]。
近年来,国内外对冲压式翼伞气动性能研究的关注度与日俱增。20世纪60年代,美国开始进行翼伞研究,从起初的空投试验、风洞试验到后来盛行的计算机仿真分析[5-9],研究表明翼伞前缘切口形式对翼伞的气动性能有很大影响。21世纪初,文献[1]和文献[10]对带前缘切口的Clark-Y翼型剖面进行了二维数值模拟;文献[11]对带有“唇部”前缘切口的Clark-Y翼型进行了研究;文献[12]通过数值计算对比分析了完整翼型、带前缘切口翼型以及带前缘切口和上翼面绕流装置翼型的气动参数。国内的研究主要集中于前缘切口形状对翼伞气动性能影响的探讨。文献[13-14]对前缘切口形状对翼伞气动性能的影响进行了初步的探讨,得出了前缘切口对翼伞影响区域限于前缘附近,压力分布同干净翼类似;降低了其失速迎角,对升力影响不大,阻力却明显增大。但全文对前缘切口的角度和长度的影响没有进行详细的讨论。
区别于上述研究成果,为了更准确地对前缘切口参数(对气动数据较为敏感)的气动性能进行对比分析,尽可能找到最适用于工程应用的参数范围,本文以某大型冲压式翼伞的基础翼型剖面为研究基础,通过改变前缘切口角度和前缘切口长度这两项参数,最终得到四种有代表性的前缘切口参数的翼型剖面,并对这四种翼型剖面进行仿真计算,以期为翼伞设计优化分析提供参考。
1 计算模型与数值方法
1.1 模型建立和网格生成
本文所选用的某大型翼伞的基础翼型剖面,如图1所示。其弦长(定义为前缘切口上端到翼型后缘点连线)=7.5m,前缘切口角度=30°,前缘切口长度=0.8m。

图1 基础翼型剖面
由于太小的前缘切口会导致翼伞充气时间过长,而非常大的切口则会使气动性能不佳,因此综合考虑前缘切口参数对气动数据较为敏感的范围,改变前缘切口角度和前缘切口长度后,得到的四种翼型剖面(Y1、Y2、Y3和Y4)的前缘切口参数,如表1所示。与其他研究者对前缘切口参数的定义不同,为了增强对计算不变量的控制,对于前缘切口角度和前缘切口长度的定义是以上翼面前缘点为不动点,切口绕其顺时针转动,从而形成更大的前缘切口角度和更小的前缘切口长度,这样能保证上翼面结构的完整性。
表1 翼型剖面前缘切口参数

Tab.1 Leading edge cut parameters of airfoil profile
二维流场域的范围根据弦长成整数倍设置,为了使翼型的流场特征都要在计算域内,根据经验,流场入口距离和上下边界距离均为5~10,出口距离为10~20。因此,文中计算时取左、上、下方距离翼型剖面前缘点(也是流场计算的坐标原点)7,右方距离后缘点12,以保证计算准确的同时降低计算成本。
网格的生成采用全流场二维非结构网格,并在近壁面处进行细化,附上边界层网格,以便更好地模拟翼型表面的流动特性。其他模型的网格均采用同样方式生成,最后的计算网格模型如图2所示,四种翼型前缘切口处的局部网格分布如图3所示。

图2 网格模型

图3 四种翼型前缘切口局部网格
1.2 计算条件和数值方法
在计算前,首先对翼型剖面计算模型做简化处理,并假设:1)翼型剖面做刚性化处理,不考虑其在气流作用下的变形;2)翼型剖面透气量为零;3)在流动情况确定的条件下,做定常流动处理。
对四种翼型剖面在选取不同攻角下展开数值计算,分析其气动参数随攻角的变化以及流场分布情况。本文计算选取-8°~32°之间的一部分攻角(即-8°,-4°,0°,4°,6°,8°,10°,12°,14°,16°,20°,24°,28°,32°)作为计算工况。计算条件为在海拔高度6km的大气条件下,来流速度为=0.111(约35m/s),声速为316m/s,具体计算条件如表2所示。
表2 翼型剖面气动计算条件

Tab.2 Aerodynamic calculation conditions of airfoil profile
由于本文研究的冲压式翼伞近似于平滑的壁面,在来流速度为35m/s的条件下,流体看作是不可压缩流。气体采用理想气体模型,雷诺数=1.7×106(其中分别是流体的密度、流速和特征长度,而是流体的动力粘度)属于高雷诺数范畴。因此本文的气动计算根据假设可以合理考虑为定常不可压湍流流动,选用标准K-epsilon湍流模型进行求解比较合适。翼伞流场满足流体力学基本控制方程为

式中为速度矢量;为通用求解变量;为广义扩散系数;为时间。
数值方法采用压力耦合方程的半隐式算法(Semi-implicit Method for Pressure-linked Equations,SIMPLE),控制方程均采用二阶离散格式,虽然其计算成本高于一阶离散格式,相同情况下的收敛速度也较慢,但一般来说,其计算精度更高,结果更为准确。
2 仿真计算及结果分析
本章节对Y1、Y2、Y3、Y4四种翼型剖面的流场压力分布情况、速度分布范围以及气动参数变化情况进行了对比分析,其结果可为翼伞的改进设计提供指导。
2.1 压力分布
为了分析四种翼型剖面附近的流场压力分布情况,取负攻角=-8°、=0°、小攻角=8°以及大攻角=20°四种典型情况来进行研究。
图4(a)为负攻角时四种翼型的压力分布图,从图中可以看出负攻角时,气流从切口上方流向翼型剖面,最先到达上翼面前端,随着前缘切口角度的增大(即前缘切口长度的减小),在前缘切口中部形成的压力梯度越来越小;在上翼面前缘点处的压力梯度向切口方向移动,上翼面的压力梯度也越来越大;下翼面的压力梯度先减小后增大,Y3翼型最小,Y4翼型又有较为明显的增大;由于切口长度的减小,更多的气流受到下翼面前缘点的阻挡,减速进入到气室内,使得气室内的压力逐渐增大,即从Y1翼型到Y4翼型气室内的压力是依次增大的。
图4(b)为0°攻角时的压力分布图,当气流从翼型上翼面前缘点处流向翼型后缘时,随着前缘切口角度的增大(前缘切口长度的减小),切口与下翼面交界点附近的气流外翻现象减弱,下翼面的压力梯度越来越小,而气室内形成的压力越来越大;同时,上翼面前缘点附近的压力梯度也越来越小,而上翼面中部的压力梯度变化并不明显。
当攻角增大到8°时,如图4(c)所示,气流迎面流向前缘切口处,随着前缘切口角度的增大(前缘切口长度的减小),在四种翼型剖面的上翼面形成的压力梯度差别不大,而下翼面前缘处的气流外翻现象越来越严重,形成的压力梯度越来越大;前缘切口中部的压力梯度变化并不明显,正攻角下流入气室内的气流受到前缘切口的阻挡很小,因此四种翼型气室内的压力分布以及压力值差别不大。这说明小攻角下,前缘切口参数只对下翼面前缘点处的压力分布有较为明显的影响。
当攻角达到20°,随前缘切口角度的增大(前缘切口长度的减小),上翼面压力梯度继续减小;下翼面前缘点不再有气流外翻,压力梯度也减小,但后缘部分压力梯度却在增大;前缘切口处压力梯度也在增大,但四种翼型气室内的压力分布基本一致。不同攻角下翼型剖面的压力云图,如图4(d)所示,由此可知,当攻角增大到一定程度后,前缘切口参数的改变对四种翼型的气动性能不再有明显影响。
(a)=-8°
(b)=0°
(c)=8°
(d)=20°
图4 不同攻角下翼型剖面的压力云图
Fig.4 Pressure contours of airfoil profile at different attack angles
2.2 速度分布
为了分析四种翼型剖面附近的流场速度分布情况,取失速攻角前后的三个攻角=12°、14°、16°作为研究对象,图5(a)给出了四种翼型在攻角=12°时的流场流线分布,可看出四种翼型剖面前缘切口附近的压力梯度均很大,但随着切口角度的增加,前缘切口处的压力梯度减小,流动分离点越来越靠近切口中心;上翼面的压力梯度也越来越大。
当攻角增大到14°时,如图5(b)所示,基础翼型(Y1)上翼面后缘处仍能较好地保持附着于翼型表面流动,Y2、Y4翼型有轻微的分离现象,而Y3翼型出现了流动分离,并产生了脱体漩涡,即Y3翼型已经达到了其失速迎角,而Y1、Y2、Y4翼型还未失速,说明Y3翼型在四种翼型里面是最易失速的。
当攻角继续增大到16°时,如图5(c)所示,四种翼型在上翼面后缘处均出现了流动分离,产生了脱体漩涡,而Y3翼型的脱体漩涡最大,影响范围也最广,其次是Y2翼型、Y4翼型、Y1翼型。这说明Y3翼型失速后气动力最容易受影响,而Y1翼型失速后气动力最不易受影响,这与其气动参数的变化情况相一致。
(a)=12°
(b)=14°
2.3 气动参数
图6为四种切口参数翼型升力系数L变化曲线图,从图中可以得到四种切口参数翼型的升力系数L均随着攻角的增大,呈现先增大后减小的趋势。其中,Y3翼型L的最大值出现在12°攻角,而Y1、Y2、Y4翼型的L最大值出现在14°攻角。在负攻角以及12°攻角以上的范围内,四种翼型的升力系数有较为明显的差别,但在正攻角范围内,Y2和Y4翼型的L差别很小。因此,单从升力系数变化曲线来看,基础翼型Y1的气动性能最好,而Y3翼型的最差,这说明Y3翼型达到失速迎角后的气动性能对攻角最为敏感。
图7为四种翼型阻力系数d随攻角的变化曲线图。在整个计算攻角范围内,四种翼型的d均呈现先缓慢减少,再缓慢增加,之后快速增长的变化趋势。在负攻角以及较大的正攻角范围,d有一定的差别:1)负攻角时,随着前缘切口角度的增大(前缘切口长度的减小),d增大,曲线上移。45°切口角度时(Y4翼型)达到最大值,这与负攻角时,气流从左上方流向翼型剖面,在大的前缘切口角度下,受到的气室内气流阻挡更大有关;2)在较大的正攻角范围内,随着前缘切口角度的增大(前缘切口长度的减小),d却有所减小,但Y2、Y3、Y4翼型间的阻力系数d差别很小。这与正攻角时,气流从左下方流向翼型剖面,在大的切口角度下受到的气室内气流阻挡变弱有关。
在0°~8°迎角范围内,d增长缓慢,并且四种翼型间相差无几。但基础翼型Y1的阻力系数d的最小值出现在0°攻角;Y2翼型的阻力系数d最小值出现在4°攻角;Y3、Y4翼型的阻力系数d最小值出现在6°攻角。
图8为四种翼型升阻比随攻角的变化曲线图,由图可直观看出:基础翼型Y1的升阻比最大值出现在10°攻角,而Y2、Y3、Y4翼型的升阻比最大值均出现在8°攻角。随着前缘切口角度的增加(前缘切口长度的减少),升阻比的最大值也增大;Y3翼型的升阻比最大;而Y4翼型的升阻比最大值又有明显的减少。在负攻角范围内,随着切口角度的增加(前缘切口长度的减少),升阻比在数值上有明显减小,在Y3翼型达到最小,之后Y4翼型的升阻比又有所增大。
图9为四种翼型剖面的俯仰力矩系数m的变化曲线图。从图中可以看出在负攻角及12°攻角以上的范围内,Y2、Y3、Y4翼型剖面始终是保持稳定的。但在负攻角时,基础翼型不稳定;在4°~12°攻角范围内,Y3翼型的稳定性最好,而Y4翼型稳定性最差。冲压式翼伞稳定滑翔阶段的俯仰角一般在10°左右,因此,总的来说,前缘切口参数对俯仰力矩系数m的影响并不大。

图6 升力系数CL变化

图7 阻力系数Cd变化
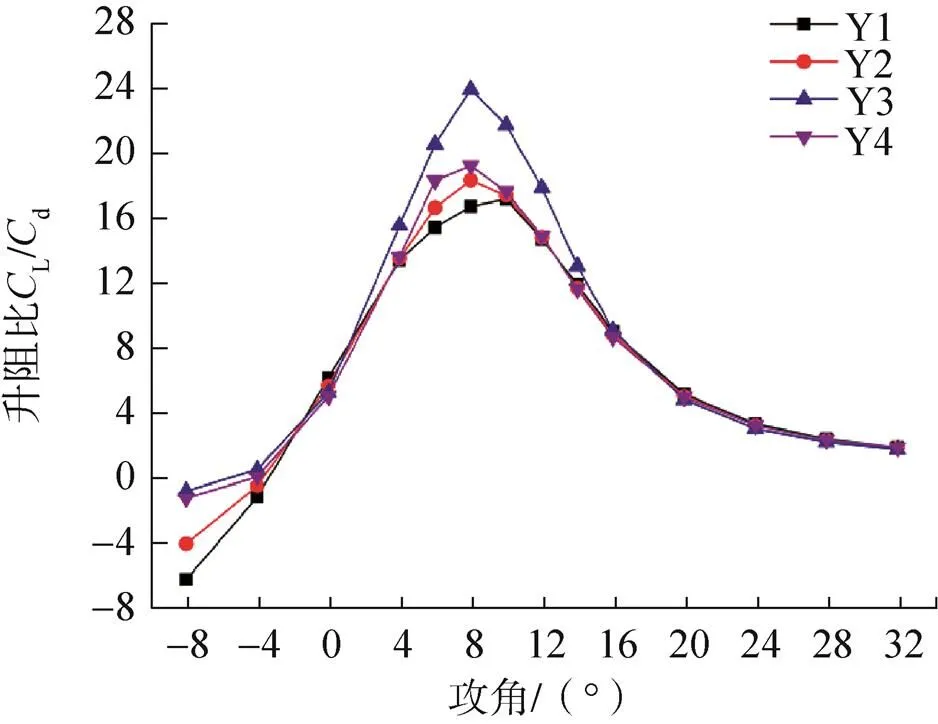
图8 升阻比CL/Cd变化

图9 俯仰力矩系数Cm变化
3 结束语
文章通过对Y1、Y2、Y3、Y4四种翼型剖面的流场压力分布情况、速度分布范围以及气动参数变化情况进行对比分析,得出以下结论,可为冲压式翼伞设计的改进和优化设计提供指导。
1)负攻角时,上翼面的压力梯度随前缘切口角度的增大而增大,而下翼面的压力梯度随前缘切口角度的增大而减小。正攻角时,上、下翼面的压力梯度对前缘切口角度并不敏感;气室内的压力分布随切口参数的变化没明显改变,只是在小攻角范围气室内的压力随攻角增大有所增大。当攻角增大到一定程度后,前缘切口参数的改变对翼型压力分布情况不再有明显影响。
2)四种翼型的升力系数随攻角的增大,均呈现出先增大后减小的趋势;阻力系数则呈现先缓慢减少,再缓慢增加,之后快速增长的变化趋势。但是前缘切口参数对翼型升力系数达到最大时和阻力系数达到最小时的攻角大小有一定的影响。
3)随着前缘切口角度的增加(即前缘切口长度的减少),翼型最大升阻比也增大,但是会有一个临界值。
4)冲压式翼伞稳定滑翔阶段的俯仰角一般在10°左右,所以前缘切口参数对俯仰力矩系数的影响不大。
本文主要通过对冲压式翼伞二维翼型剖面进行了研究,在计算条件允许的情况下开展三维气动计算能更准确地分析翼伞表面的流动情况,从而为工程应用提供更有价值的参考。
[1] MITTAL S, SAXENA P, SINGH A. Computation of Two-dimensional Flows Past Ram-air Parachutes[J]. International Journal for Numerical Methods in Fluids, 2001, 35(6): 643-667.
[2] NICOLAIDES J D. Parafoil Wind Tunnel Tests[R]. Indiana: University of Notre Dame, AD731564, 1971.
[3] BERGERON K, WARD M, COSTELLO M. Aerodynamic Effects of Parafoil Upper Surface Bleed Air Actuation[C]//AIAA Atmospheric Flight Mechanics Conference, Minneapolis, Minnesota, 2012.
[4] GAVRILOVSKI A, WARD M, COSTELLO M. Parafoil Control Authority with Upper-surface Canopy Spoilers[J]. Journal of Aircraft, 2015, 49(5): 1391-1397.
[5] KNACKE T W. Parachute Recovery Systems: Design Manual[M]. Parachute Publishing, USA, 1991.
[6] ROSS J. Computational Aerodynamics in the Design and Analysis of Ram-air-inflated Wings[C]//Raes/AIAA, Aerodynamic Decelerator Systems Technology Conference, London, 1993.
[7] LINGARD J S. Precison Aerial Delivery Seminar Ram-air Parachute Design[R]. Clearwater Beach: Proceedings of Aiaa Aerodynamic Decelerator Systems Technology Seminar AIAA, 1995.
[8] LINGARD J. The Aerodynamics of Gliding Parachutes[C]//Aerodynamic Decelerator and Balloon Technology Conference, Albuquerque, USA, 1986.
[9] 陆伟伟, 张红英, 连亮. 大型翼伞的三维气动性能分析[J]. 航天返回与遥感, 2015, 36(3): 1-10. LU Weiwei, ZHANG Hongying, LIAN Liang. A Three-dimensional Analysis on Aerodynamic Performance of a Large Parafoil[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(3): 1-10. (in Chinese)
[10] BALAJI R, MITTAL S, RAI A K. Effect of Leading Edge Cut on the Aerodynamics of Ram-air Parachutes[J]. International Journal for Numerical Methods in Fluids, 2005, 47(1): 1-17.
[11] MOHAMMADI M A, JOHARI H. Computation of Flow over a High-performance Parafoil Canopy[J]. Journal of Aircraft, 2015, 47(4): 1338-1345.
[12] BERGERON K, WARD M, COSTELLO M. Aerodynamic Effects of Parafoil Upper Surface Bleed Air Actuation[C]//AIAA Atmospheric Flight Mechanics Conference, Minneapolis, Minnesota, USA, 2012.
[13] 朱旭, 曹义华. 翼伞弧面下反角、翼型和前缘切口对翼伞气动性能的影响[J]. 航空学报, 2012, 33(7): 1189-1200. ZHU Xu, CAO Yihua. Effects of Arc-anhedral Angle, Air-foil and Leading Edge Cut on Parafoil Aerodynamic Performance[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(6): 1189-1200. (in Chinese)
[14] 聂帅, 曹义华, 田似营. 前缘切口对翼伞气动性能的影响[J]. 航空动力学报, 2016, 31(6):1477-1485. NIE Shuai, CAO Yihua, TIAN Siying. Effect on Parafoil Aerodynamic Performance of Leading Edge[J]. Journal of Aerospace Power, 2016, 31(6): 1477-1485. (in Chinese)
[15] MADSEN C M, CERIMELE C J. Flight Perfromance, Aerodynamics, and Simulation Development for the X-38 Parafoil Test Program [C]//Aerodynamic Decelerator Systems Technology Conference Monterey, California, USA, 2003.
[16] ALTMANN I H. Numerical Simulation of Parafoil Aerodynamics and Dynamic Behavior[C]//AIAA Structures, Structural Dynamics, and Materials Conference, California, USA, 2009.
[17] KALRO V, TEZDUYAR T E. A Parallel 3D Computational Method for Fluid–structure Interactions in Parachute Systems[J]. Computer Methods in Applied Mechanics & Engineering, 2000, 190(3-4): 321-332.
[18] STEIN K, BENNEY R, KALRO V, et al. Parachute Fluid–structure Interactions: 3-D Computation[J]. Computer Methods in Applied Mechanics & Engineering, 2000, 190(3-4): 373-386.
(编辑:陈艳霞)
Analysis of Leading Edge Cut Parameters on Performance of Large Ram-air Parachute
HUANG Yan ZHANG Hongying YANG Luyu CHEN Jianping TONG Mingbo
(Ministerial Key Discipline Laboratory of Advanced Design Technology of Aircraft, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
In addition to the structure parameters of the airfoil profile, the angle and the length of leading edge cut are the main parameters that affect the aerodynamic performance of the ram-air parachute. In this paper, based on the fundamental airfoil profile of the large ram-air parachute, two important parameters, the angle and the length of leading edge cut, are changed and four kinds of airfoil profile with representative parameters of leading edge cut can be obtained in order to find the range of engineering applications on leading edge cut parameters more accurately. The numerical calculation method is adopted to study the aerodynamic performance of four airfoils and the results show that the pressure gradient of upper surface grows and the pressure gradient of lower surface decreases with the increase of the angle of the leading edge cut at negative angles of attack, while the angle of leading edge cut does not have significant effect on the pressure gradient of the upper and lower surface at positive angles of attack. With the increase of the angle of leading edge cut, the maximum lift-drag ratio of the airfoils also increases, but there will be a threshold. The influence of the leading edge cut parameters on the pitch moment coefficient is not significant. The results of this paper provide some reference value for design and optimization of ram-air parachute.
angle of leading edge cut; length of leading edge cut; aerodynamic performance; ram-air parachute
V411.3
A
1009-8518(2017)05-0010-08
10.3969/j.issn.1009-8518.2017.05.002
黄炎,男,1993年生,2016年获南京航空航天大学飞行器设计与工程专业学士学位,现在南京航空航天大学航空工程专业攻读硕士学位。研究方向为降落伞设计。E-mail:1012269519@qq.com。
2017-05-23
航空科学基金(2016ZC 52031)

