单相级联多电平H桥整流器有限集模型预测电流控制

蒋 蔚， 刘 碧， 曹梦华， 谢望玉， 宋文胜

(1. 西南交通大学电气工程学院， 四川 成都 610031；2. 中国铁道科学研究院机车车辆所， 北京 100081)

单相级联多电平H桥整流器有限集模型预测电流控制

蒋 蔚1， 刘 碧1， 曹梦华1， 谢望玉2， 宋文胜1

(1. 西南交通大学电气工程学院， 四川 成都 610031；2. 中国铁道科学研究院机车车辆所， 北京 100081)

本文以基于电力电子变压器的高速列车牵引传动系统中的单相级联多电平H桥整流器为控制对象，以提升系统动态响应速度、减小网侧电流谐波含量为控制目标，提出了一种基于两矢量的有限集模型预测电流控制算法。首先，推导单相级联多电平H桥整流器的α-β静止坐标系下数学模型；然后，基于空间矢量调制思想，对单相级联多电平整流器进行基本电压矢量定义与空间扇区划分；在此基础上，建立包含最小电流误差的目标函数，通过对其求导实时计算出两个矢量的最优占空比，同时为了保证各模块直流侧电容电压的平衡关系，设计了选取冗余矢量的原则。与基于PI的瞬态电流控制算法相比，所提出的模型预测控制算法无需内环PI控制器，显著提高了电流内环的动态响应速度；最后，对所提算法与传统的瞬态电流控制算法进行硬件在环半实物实验对比研究，结果表明了所提算法的可行性与有效性。

级联多电平H桥整流器； 单相； 模型预测控制； 电容电压平衡； 直接电流控制

1 引言

在高速铁路技术发展过程中，传统的工频牵引变压器存在着体积庞大、笨重、效率低下等缺点，严重阻碍了高速列车动力与速度的提升，因此，实现高速列车牵引传动系统的轻量化是亟待解决的难题之一[1,2]。基于电力电子变压器的牵引传动技术是目前较为典型的解决方案。在该系统的拓扑结构中，作为前级输入的单相级联H桥整流器，具有模块化、易于维护、电压均衡易实现等优点，其控制性能的优越性将对后级的全桥隔离DC-DC变换器乃至整个负载系统产生巨大的影响，因此对其研究具有重要的意义[3,4]。

在单相脉冲宽度调制(Pulse Width Modulation，PWM)整流器众多控制方法中，按照内环被控对象的不同可分为直接电流控制与直接功率控制。目前直接电流控制已在单相PWM整流器中得到广泛应用，它包括滞环电流控制[5]、瞬态电流控制[6]、dq电流解耦控制[7-9]、预测电流控制[10-12]等。其中，滞环电流控制结构比较简单，电流跟踪和控制特性非常好，但其电流谐波含量大，且开关频率具有随机性，容易造成系统不稳定。瞬态电流控制具有良好的动态特性，并且由于电流内环的存在，过流保护非常容易实现。dq电流解耦控制方法通过独立控制交流侧电流有功和无功分量，从而实现系统有功和无功功率的解耦控制，其零稳态误差均能达到较高要求，但由于存在多个PI控制器，系统动态响应较慢。

随着人们对PWM整流器的研究深入，越来越多的预测控制方案被提出。模型预测控制(Model Predictive Control, MPC)作为一种新颖的控制方式，具有控制方式灵活、动态性能良好、鲁棒性强等优点，近年来已逐渐推广应用于电力电子与电力传动领域。传统MPC中，利用电力电子器件开关的离散特性，分别计算出不同的电压矢量对系统状态的影响，在线优化寻求最小的目标函数，并进行滚动优化，从而预测出下一个控制周期的最优开关序列[13]。文献[14]通过构建目标函数，选出系统所期望的最优电压矢量，该方法动态响应迅速、控制灵活，易处理约束优化；但是其矢量个数有限，必须采用较高开关频率，造成系统开关损耗过大，而且其开关频率不固定，造成电流谐波分布不规律。针对上述问题，文献[15]通过加入数字滤波器有效地实现了定频控制，但采样频率同样过高。文献[16]提出一种基于占空比优化的模型预测控制方法，它将零矢量与非零矢量以占空比的方式相结合，获得了更好的功率跟踪效果；但该方法难以解决有功、无功功率同时优化的问题。基于MPC的单相PWM整流器近年来受到了广泛关注，而MPC在级联H桥多电平整流器上的应用却鲜有研究。

本文以单相级联多电平H桥整流器为研究对象，为了提升系统的动态特性，提出了基于有限集的模型预测电流控制(Finite Control Set Model Predictive Current Control，FCS-MPCC)，并针对传统模型预测控制中电流谐波含量大、开关频率不固定等缺点进行改善。所提算法首先划分了单相级联多电平H桥整流器的空间矢量扇区，在每个开关周期内，根据所设计的目标函数以及各模块之间的电容电压平衡关系，选择出扇区边界的两个矢量，合成等效参考电压矢量。最后，本文对所提出的优化算法和传统瞬态电流控制算法进行了计算机仿真与半实物实验对比研究，验证了所提算法的有效性与可行性。

2 单相级联H桥整流器数学模型

单相级联H桥七电平整流器拓扑结构如图1所示。三个H桥整流器输入端通过级联的形式叠加起来，并通过网侧电感和网侧等效电阻接入电网，每个H桥直流侧相互独立。为了方便分析该结构的工作原理，本文先对单个功率模块进行分析。

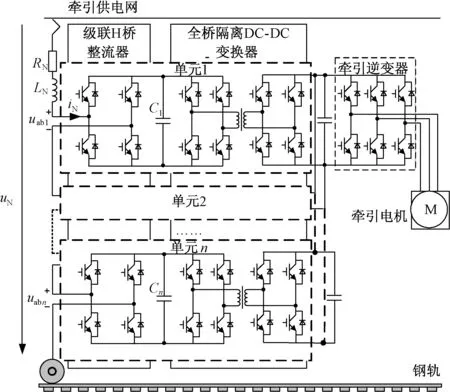
图1 基于H全桥结构的PET列车牵引传动系统拓扑图Fig.1 Topology of PET train traction transmission system based on H-bridge structure

由于单相级联多电平H桥整流器网侧电阻很小，可以忽略，其基尔霍夫电压平衡方程可以表示为：

(1)

式中，LN为网侧电感器与线路等效电感之和；RN为网侧电阻与线路电阻之和；uN与iN分别为网侧电压和电流；uabk为第k个H桥的输入端电压。

通过正交延迟构造的网侧电压与电流在静止坐标系下的方程为：

(2)

(3)

式中，UNm和INm分别为网侧电压电流的幅值；uNα、iNα分别为网侧电压和电流在α轴上的分量；uNβ、iNβ分别为网侧电压和电流在β轴上的分量；φ为网侧电压电流的相位差。单相级联多电平H桥整流器在αβ静止坐标系下的方程为：

(4)

式中，uabα、uabβ为输入端电压uab在α轴和β轴上的分量。为了便于分析，定义第k个模块的理想二值逻辑开关函数Ski(k=1, 2, …,n；i=a, b)：

(5)

(6)

第k个模块输入端电压uabk可由开关函数Ski表示为：

uabk=(Ska-Skb)udck

(7)

式中，udck为第k个模块直流侧电压。

则级联H桥整流器的输入端电压uab为：

(8)

根据级联H桥整流器与每个功率模块的拓扑关系，可以推出级联H桥整流器在α-β坐标系下的数学模型为：

(9)

式中，Skaα、Skaβ为Ska在α轴与β轴上的坐标分量；Skbα、Skbβ为Skb在α轴与β轴上的坐标分量。

由式(9)可以得到网侧电压电流的变化率为：

(10)

采用前向欧拉法，可以得到式(10)的离散化表达式为：

(11)

式中，Ts为系统的采样周期；iNα(k)、iNβ(k)分别为当前k时刻αβ轴的电流值；iNα(k+1)、iNβ(k+1)分别为k+1时刻αβ轴的电流值。

由式(5)和式(6)可知，每个H桥模块有四种开关模式，它们对直流侧电容电压的影响如表1所示。可以看出，在不同的开关模式下，各模块对直流侧电容电压的影响不同。例如，当输入电流为正时，若某模块开关模式为01，则其电容电压会下降，且下降程度最为明显。

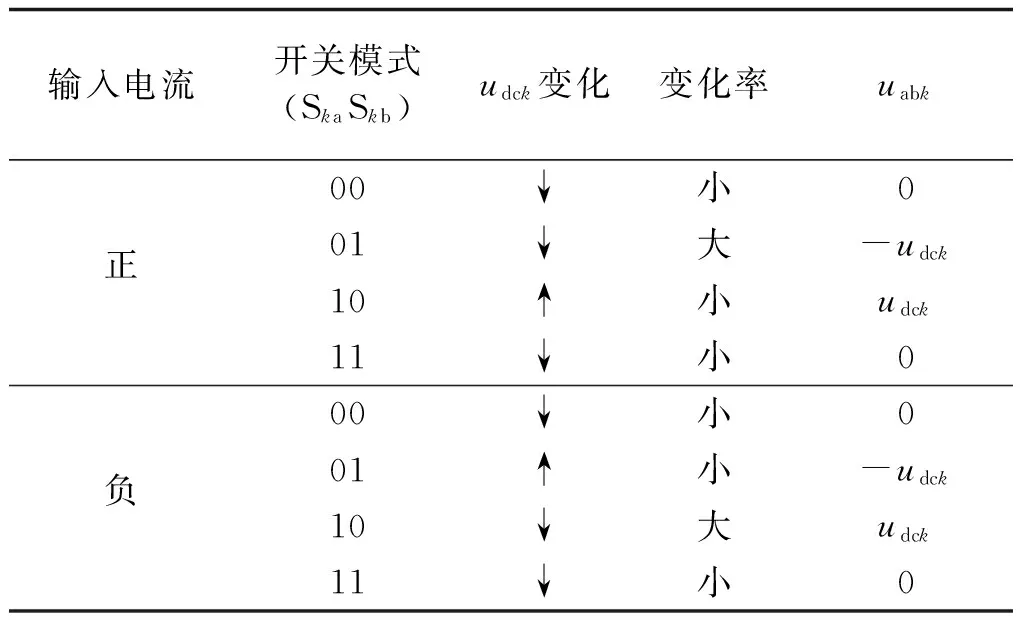
表1 不同工作状态对直流侧电压的影响Tab.1 Influence of different operating conditions on DC voltage

3 本文所提FCS-MPCC算法

FCS-MPCC算法的基本原理为：在每一个控制周期的开始时刻，根据系统参数和采样参数，利用离散化表达式得到下一时刻的预测值，通过构建目标函数，在线寻优得到使目标函数最小所对应的开关矢量，作用于下一时刻。本文所提出的FCS-MPCC算法中建立的目标函数表达式为：

(12)

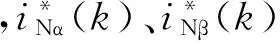
由于整流器的开关状态有限，传统的FCS-MPCC在每个开关周期只选取了一个开关矢量，其控制精度难以保证，且开关频率不固定，电流谐波含量大。为了克服以上缺点，本文所提 FCS-MPCC算法通过对级联多电平H桥整流器进行空间矢量扇区划分，在每个开关周期内选用所选扇区的两个矢量，从而减小电流谐波含量，同时保持较快的动态响应。

3.1扇区划分与判断

借鉴单相SVPWM的思想，这里对单相n电平级联H桥整流器进行扇区划分，如图2所示。

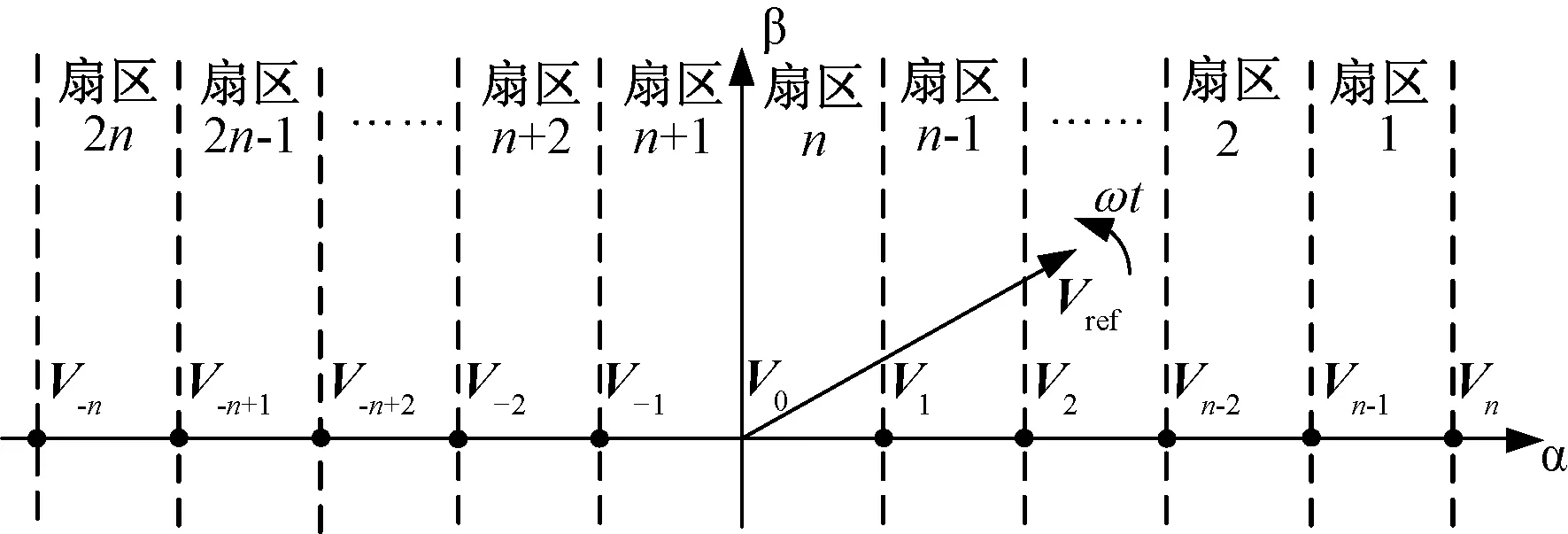
图2 扇区划分与基本矢量定义示意图Fig.2 Sector partition diagram

⋮

⋮

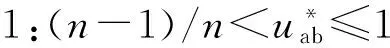
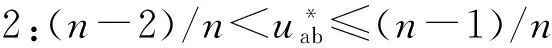
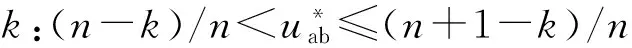
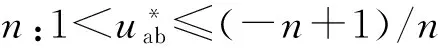
3.2矢量合成与占空比计算

根据单相级联多电平H桥整流器的2n+1种电平状态，定义对应的2n+1个基本矢量，如图2所示。在一个开关周期Ts内，可通过选择某个扇区内两个基本矢量Vg和Vg+1来合成该扇区的参考电压矢量Vref，其中，Vg和Vg+1的幅值|Vg|和|Vg+1|的幅值满足：

(13)

式中，g为区间[-n,n-1]内的整数。

根据式(10)可知，矢量Vg+1和Vg对应的电流变化率分别为：

(14)

式中，Udc为各模块直流侧电压之和，即

(15)

在实际系统中，β轴调制信号uabβ为零。在当前k时刻，任意一个扇区内的两个基本矢量分别作用一段时间后，可以预测得到下一时刻的电流为：

(16)

由式(16)可知，矢量Vg作用的时间tg决定了下一时刻的电流值，当矢量Vg作用时间tg取得最优时，对应的目标函数能够取得最小值，此时，目标函数J的导数为零，表示如下：

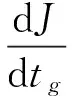
(17)

将式(12)和式(16)代入式(17)中，可以得到矢量Vg+1与Vg的作用时间tg+1、tg分别为：

(18)

若矢量Vg+1作用时间tg+1大于控制周期Ts，则取tg+1=Ts，若tg+1小于Ts，则取tg+1=0。

将Vg+1与Vg的最优作用时间tg+1、tg代入目标函数，可得：

(19)

式中，J(g)(k)为矢量Vg所对应的目标函数。

比较各个扇区边界基本矢量Vg对应的目标函数，并选择其中最小的目标函数Jmin。Jmin对应于扇区内的基本矢量作用最优时间，可以使静止坐标轴电流分量快速精确地跟踪上给定值。

3.3电容电压平衡控制与脉冲生成

由图2可知，每个基本矢量存在冗余矢量，它们对直流侧电容进行充放电，影响着各个H桥模块的直流侧电压大小，所以，需要根据各H桥模块直流侧电容电压的大小关系来选取冗余电压矢量。每个开关周期内作用的两个基本矢量所对应的冗余矢量对各模块直流侧电容电压影响一致。例如，以iN>0和3个H桥为例，当扇区2对应的目标函数最优时，若第一个H桥模块电容电压最大，则选择两个矢量(0 1 1)，(-1 1 1)，这样可以保持各模块电容电压的动态平衡。

当确定了两个矢量之后，在一个开关周期内，为了减小电流谐波，矢量作用顺序应具有对称性，矢量作用时序遵循：

Vg→Vg+1→Vg→Vg+1→Vg

(或Vg+1→Vg→Vg+1→Vg→Vg+1)

其对应的作用时间为：

tg/4→tg+1/2→tg/2→tg+1/2→tg/4

(或tg+1/4→tg/2→tg+1/2→tg/2→tg+1/4)

以3个H桥的扇区2和扇区6为例，若选择扇区2的两个矢量分别为Vg+1=V2(0 1 1)与Vg=V1(0 0 1)，扇区6的两个矢量分别为Vg+1=V-2(-1 -1 0)与Vg=V-3(-1 -1 -1)，该调制算法在这两个扇区下的矢量作用时序图以及输入端电压与网侧电流变化趋势如图3所示。

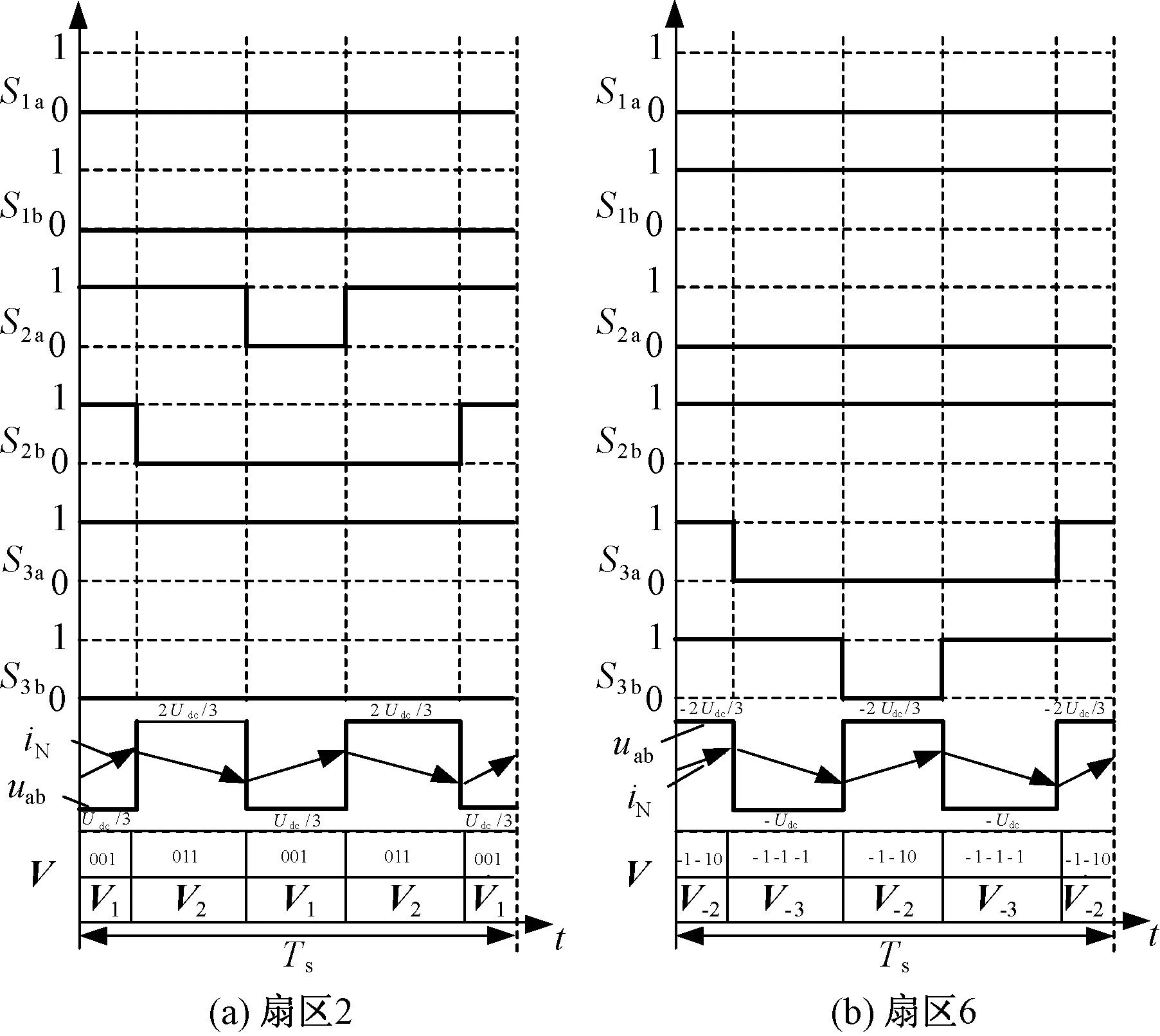
图3 SVPWM调制算法示意图Fig.3 Diagram of SVPWM modulation algorithm

从图3可以看出，在一个开关周期Ts内，网侧电流变化了四次，该调制算法所引起的网侧电流高次谐波分布在两倍开关频率附近。

3.4本文所提FCS-MPCC算法的实现

本文所提FCS-MPCC保留了传统单矢量MPCC算法的基本框架，通过预测下一时刻的电流信息来确定目标函数。而针对单相级联H桥整流器，本文所提FCS-MPCC算法对其划分扇区，通过对目标函数求导的方式来求解最优占空比与最优矢量，并通过选择合适的冗余矢量实现电压平衡控制，经过SVPWM调制产生脉冲信号。其控制系统框图如图4所示。

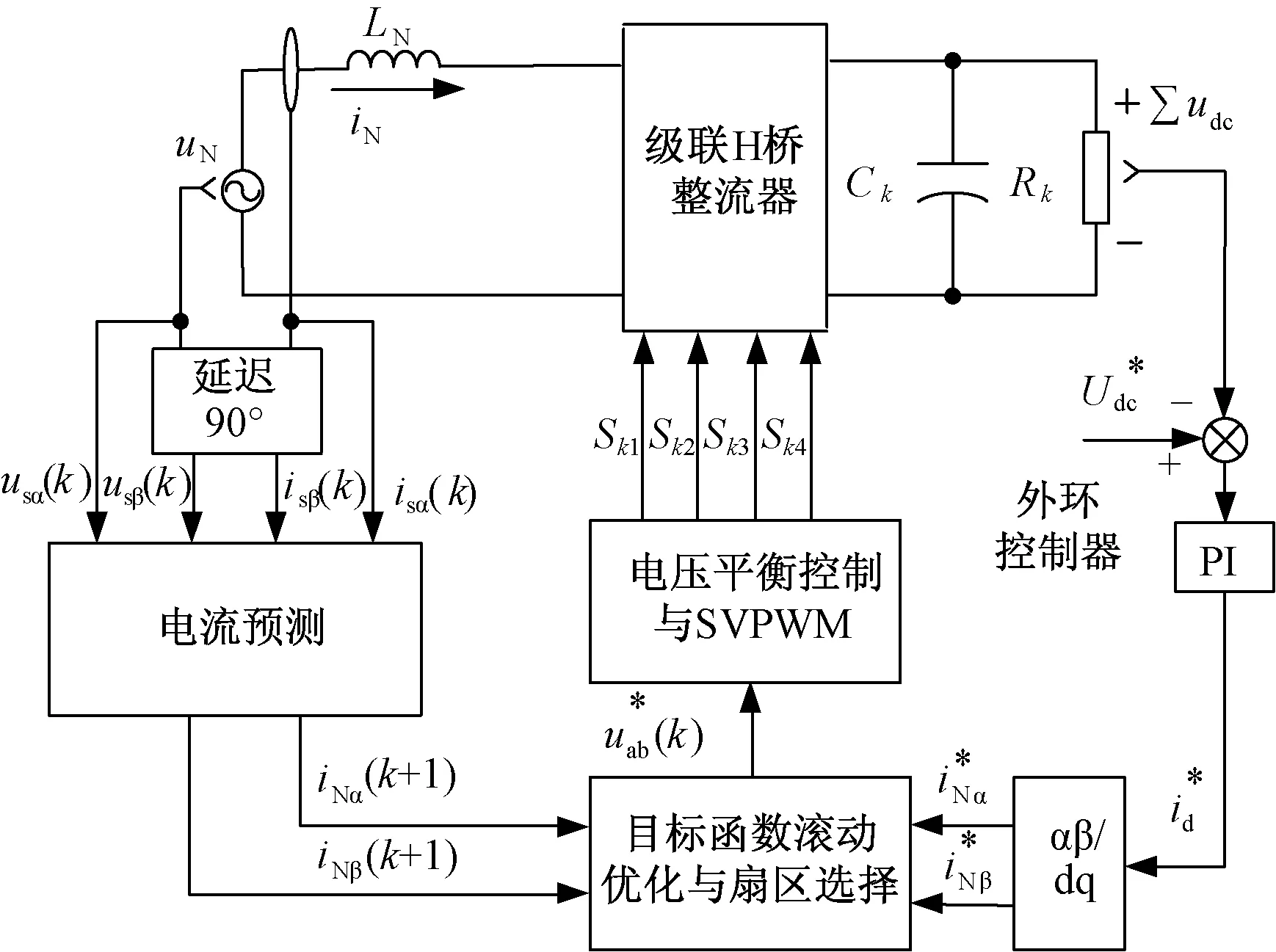
图4 模型预测电流控制系统框图Fig.4 Block diagram of adopted model predictive current control system

4 实验验证

为了验证本文所提FCS-MPCC的正确性，以单相七电平级联H桥整流器为例，对本文所提算法与传统PI瞬态电流控制算法在基于TMS32028335的RT-LAB半实物实验平台分别进行仿真和实验对比分析。表2给出了半实物实验系统的实验参数。

表2 半实物平台参数Tab.2 Experimental system parameters

图5给出了稳态情况下传统瞬态电流控制与本文所提FCS-MPCC算法的网侧电压与电流的波形。由图5(b)可知，本文所提出的FCS-MPCC很好地实现了网侧电流电压同相位，且网侧电流正弦度较高。

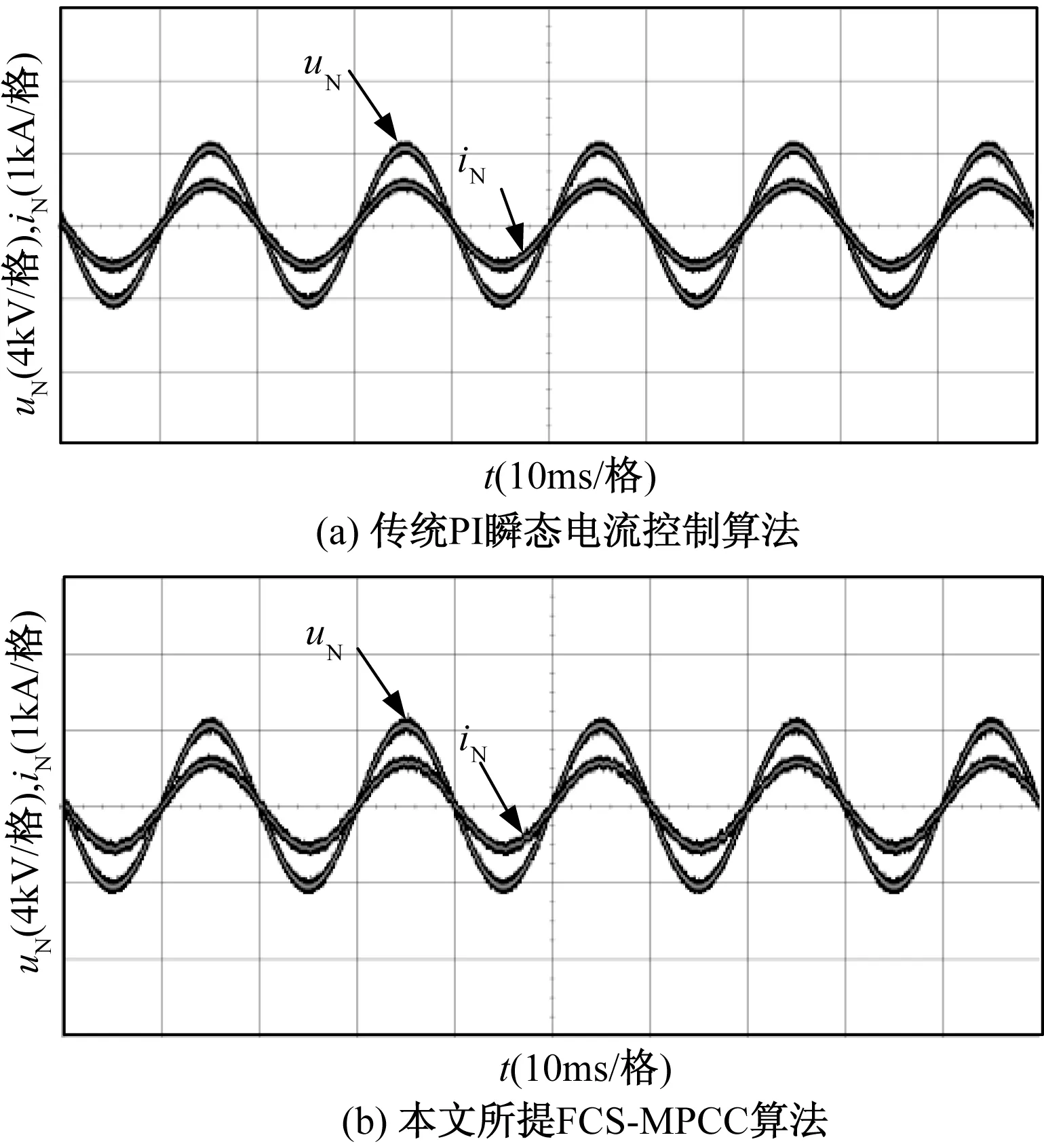
图5 两种算法稳态电压电流实验结果Fig.5 Experimental results of main voltage and line current in steady state

图6为瞬态电流控制与两矢量MPCC算法的直流侧电压与输入端电压“七电平”波形，可以清晰地看到，本文所提FCS-MPCC在稳态时实现了电容电压平衡。

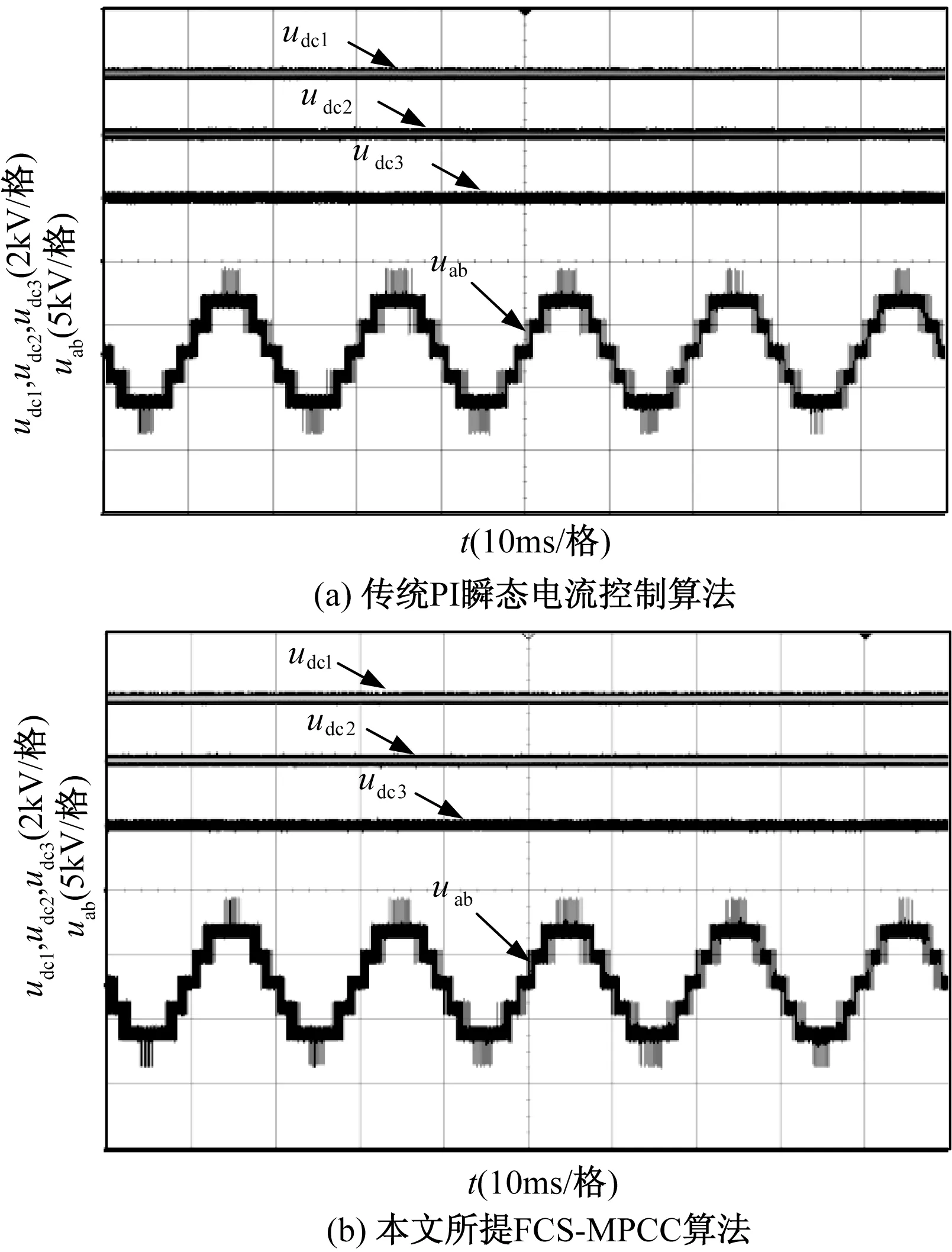
图6 两种算法稳态电容电压与输入端电压实验结果Fig.6 Experimental results of DC-link three capacitors’ voltages and input voltage

图7给出了稳态情况下瞬态电流控制与本文所提FCS-MPCC的FFT分析电流谐波含量图。可以看出，本文所提FCS-MPCC算法的高次谐波主要分布在2倍开关频率5kHz附近，总谐波失真(THD)为3.77%，与瞬态电流控制近似。由此可知，本文所提FCS-MPCC算法能良好地保持稳态精度。

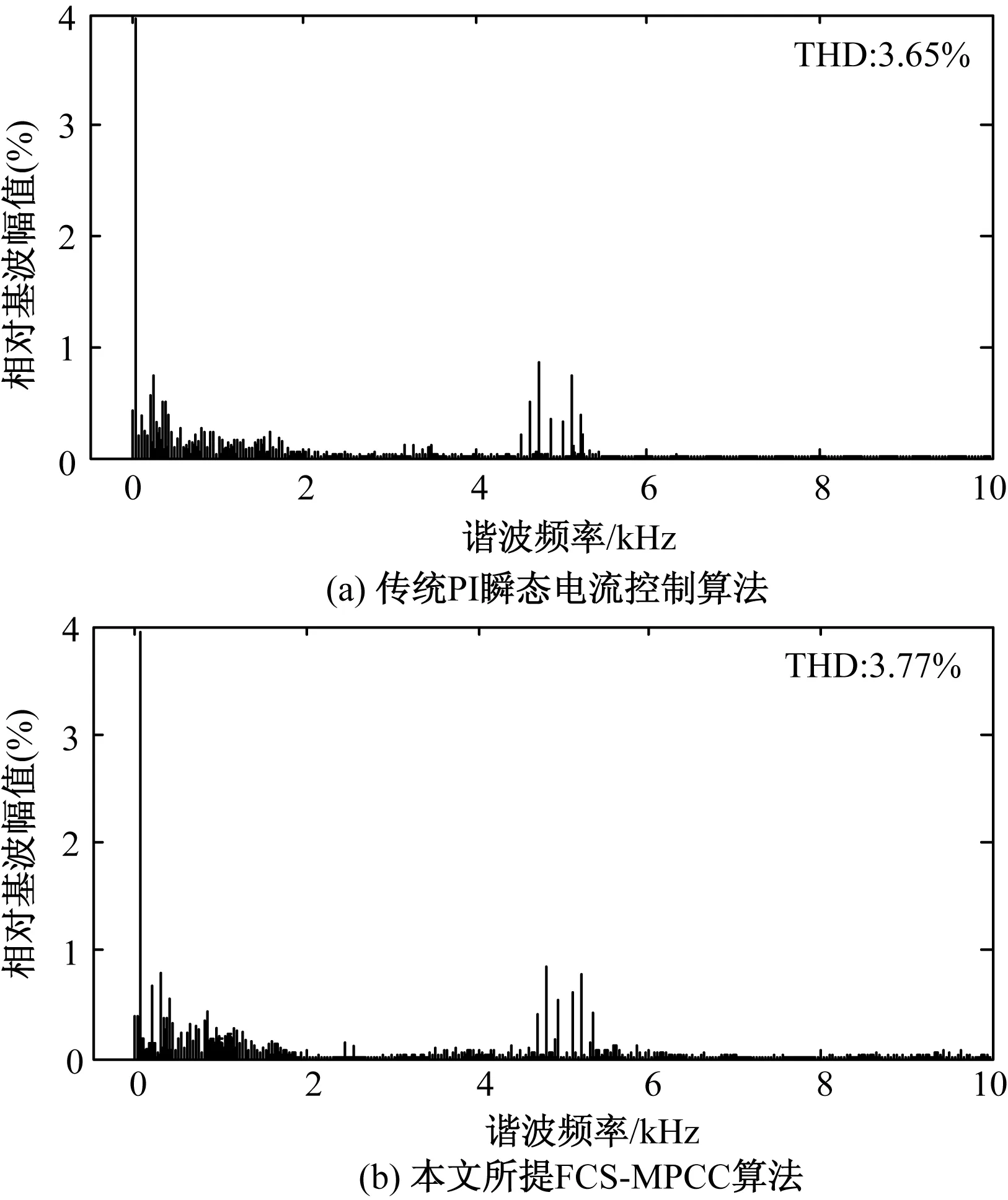
图7 网侧电流波形FFT分析实验结果Fig.7 FFT analysis result of line current of adopted scheme in experiment

图8给出了负载由额定负载突变为两倍额定负载时的实验结果。与内环相比，电压外环PI控制器速度较慢，电流内环对负载突变所产生的效果不明显，因此，在这种情况下，电压外环起主导作用。由图8可知，两种控制在经历8个工频开关周期后达到稳定。

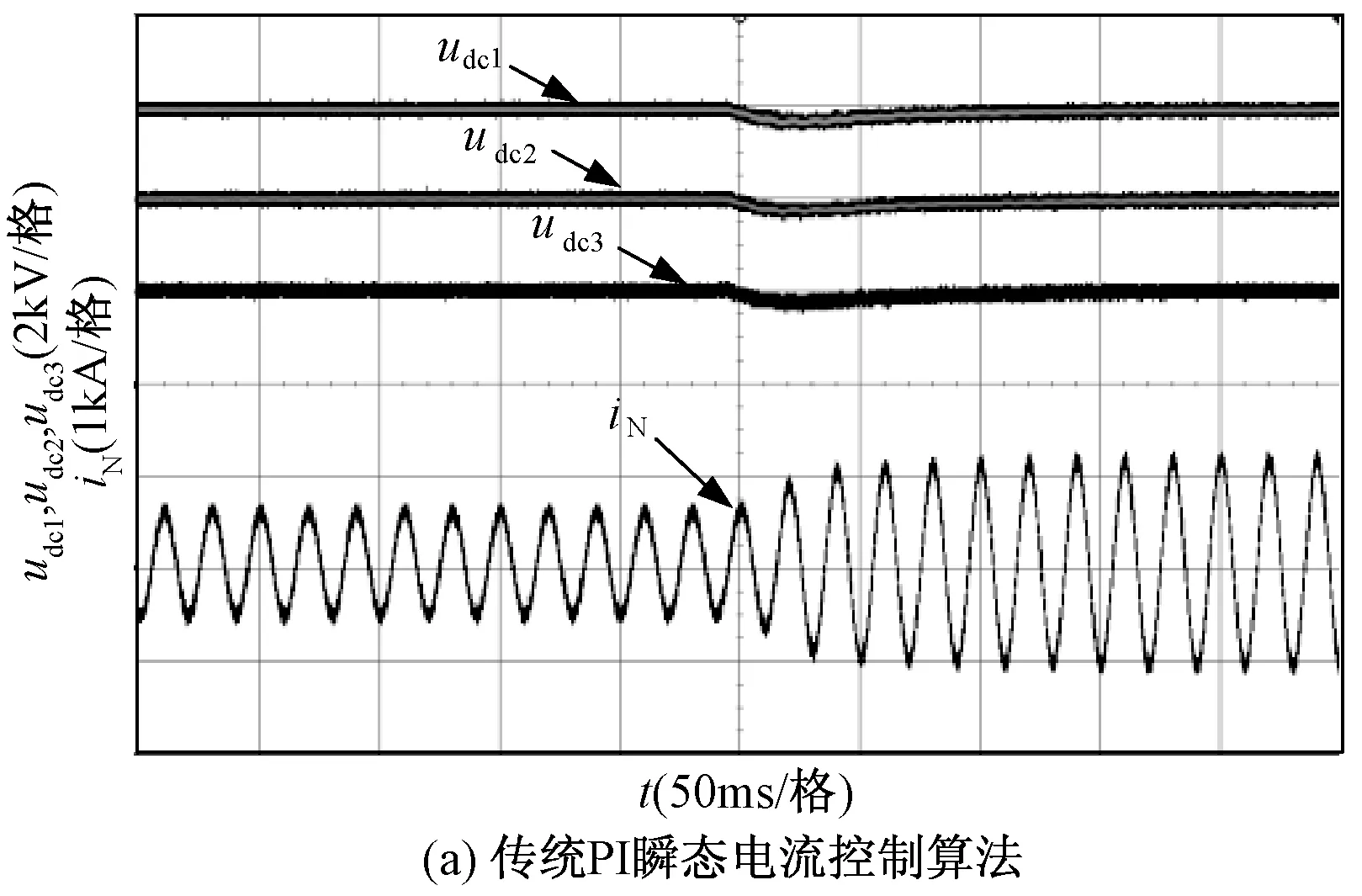
图8 两种算法在负载突变情况下的动态响应实验结果Fig.8 Experimental results of dynamic response of both algorithms under load step-change condition

图9 两种算法在电流突变情况下的实验结果Fig.9 Experimental results of currents in these two schemes under current step-change condition

通过半实物实验，将瞬态电流控制与本文所提FCS-MPCC算法进行性能对比，结果如表3所示。

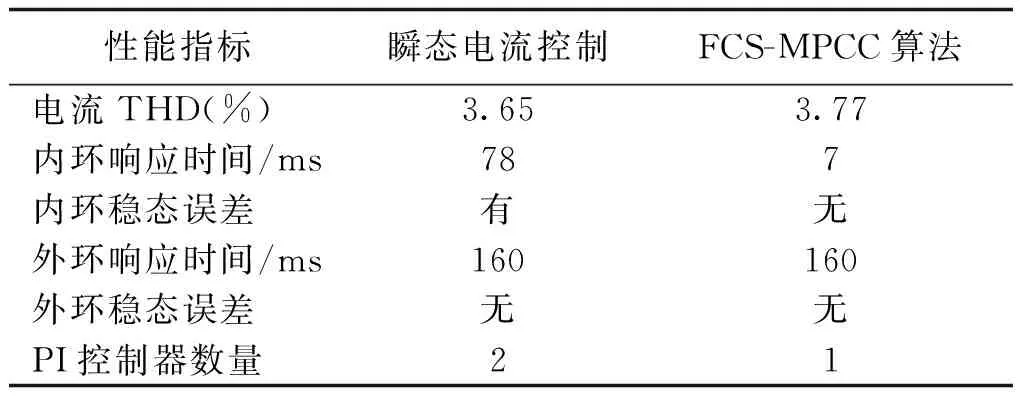
表3 两种控制算法的性能对比Tab.3 Comparison of performance for two control schemes

5 结论

本文以单相级联多电平H桥整流器为研究对象，以提高系统响应速度，减小电流谐波为控制目标，提出了一种基于两矢量的FCS-MPCC算法，并对级联多电平整流器进行空间扇区划分。通过半实物实验对比研究，验证了该算法的可行性。本文所提FCS-MPCC算法的特点可总结如下：

(1)实现了单相级联多电平H桥整流器的电容电压平衡。

(2)与传统瞬态电流控制算法相比，无需内环PI控制器，简化了参数设计。且电流内环具有快速动态响应，可实现无稳态电流误差跟踪。

(3)由于采用扇区划分判断，有效简化了每个控制周期内的最小评价函数估算次数。

(4)两个矢量合成方法保证了该FCS-MPCC算法具有恒定开关频率。

[ 1] 王顺亮，宋文胜，冯晓云(Wang Shunliang，Song Wensheng，Feng Xiaoyun). 基于电压补偿分量注入的单相级联H桥载波控制与电容电压平衡方法(Carrier-based modulation and capacitor voltage balance control method with voltage offset injection of single phase cascaded H-bridge rectifiers) [J]. 中国电机工程学报(Proceedings of the CSEE)， 2015，35(12)：3117-3123.

[ 2] 陈启超，纪延超，潘延林，等(Chen Qichao，Ji Yanchao, Pan Yanlin，et al.). 配电系统电力电子变压器拓扑结构综述(Review of power electronic transformer topologies applied to distribution system) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015, 34(3)：41-48.

[ 3] 王杉杉，王玉斌，林意斐，等(Wang Shanshan，Wang Yubin，Lin Yifei，et al.). 级联型电力电子变压器电压与功率均衡控制方法(Voltage and power balance control for cascaded multilevel converter based power electronic transformer) [J]. 电工技术学报(Transactions of China Electrotechnical Society)，2016，31(22)：92-99.

[ 4] 侯聂，宋文胜(Hou Nie，Song Wensheng). 全桥隔离DC/DC变换器的三重相移控制及其软启动方法(Full-bridge isolated DC/DC converters with triple-phase-shift control and soft starting control method)[J]. 中国电机工程学报(Proceedings of the CSEE)，2015，35(23)：6113-6121.

[ 5] 毛惠丰，孔德鹏，陈增禄，等(Mao Huifeng，Kong Depeng，Chen Zenglu，et al.). 一种单相H桥电压型逆变器三电平滞环电流跟踪控制方法(A new three-level hysteresis current controlled single-phase H-bridge voltage source inverters)[J]. 中国电机工程学报(Proceedings of the CSEE)，2015，35(15)：3904-3911.

[ 6] Brenna M, Foiadelli F, Zaninelli D. New stability analysis for tuning PI controller of power converters in railway application[J]. IEEE Transactions on Industrial Electronics， 2011，58(2)：533-543.

[ 7] 马俊鹏，宋文胜，王顺亮，等(Ma Junpeng， Song Wensheng，Wang Shunliang，et al.). 单相三电平脉冲整流器无差拍预测直接功率控制(Deadbeat predictive direct power control of single-phase three-level pulse rectifiers)[J]. 中国电机工程学报(Proceedings of the CSEE)，2015，35(4)：935-943.

[ 8] 宋文胜，冯晓云，谢望玉，等(Song Wensheng，Feng Xiaoyun，Xie Wangyu，et al.). 单相三电平整流器d-q坐标系下的控制与SVPWM方法(Space vector pulse width modulation and control techinique for single phase three level rectifier in d-q coordinate system)[J]. 电机与控制学报(Electric Machines and Control)，2012，16(4)：56-63.

[ 9] Salaet J，Alepuz S，Gilabert A，et al. D-Q modeling and control of a single-phase three-level Boost rectifier with power factor correction and neutral-point voltage balancing[A]. IEEE 33rd Annual IEEE Power Electronics Specialists Conference[C]. 2002. 2：514-519.

[10] 杨立永，杨烁，张卫平，等(Yang Liyong，Yang Shuo，Zhang Weiping，et al.). 单相PWM整流器改进无差拍电流预测控制方法(The improved deadbeat predictive current control method for single-phase PWM rectifiers)[J]. 中国电机工程学报(Proceedings of the CSEE)，2015，35(22)：5842-5850.

[11] Hung G K，Chang C C，Chen C L. Analysis and implementation of a delay-compensated deadbeat current controller for solar inverters[J]. IEE Proceedings - Circuits, Devices and Systems，2001, 148(5)：279-286.

[12] Holmes D G，Martin D A. Implementation of a direct digital predictive current controller for single and three phase voltage source inverters[A]. IEEE Industry Applications Conference, Thirty-first IAS Annual Meeting[C]. 1996. 2：906-913.

[13] Kouro S，Corté P, Vargas R，et al. Model predictive control-A simple and powerful method to control power converters[J]. IEEE Transactions on Industrial Electronics， 2009, 56(6)：1826-1838.

[14] Rodríguez J，Pontt J，Silva C A，et al. Predictive current control of a voltage source inverter[J]. IEEE Transactions on Industrial Electronics，2007，54(1)：495-503.

[15] Cortés P，Rodríguez J，Quevedo D E，et al. Predictive current control strategy with imposed load current spectrum[J]. IEEE Transactions on Power Electronics， 2008，23(2)：612-618.

[16] Zhang Y C，Xie W，Li Z X，et al. Model predictive direct power control of a PWM rectifier with duty cycle optimization[J]. IEEE Transactions on Power Electronics，2013，28(11)：5343-5351.

Finite-control-setmodelpredictivecurrentcontrolschemeforsinglephasecascadedmultilevelHbridgerectifiers

JIANG Wei1， LIU Bi1， CAO Meng-hua1， XIE Wang-yu2， SONG Wen-sheng1

(1. School of Electrical Engineering， Southwest Jiaotong University， Chengdu 610031，China; 2. Locomotive & Car Research Institute， China Academy of Railway Sciences， Beijing 100081， China)

This paper focuses on a single phase cascaded multilevel H bridge rectifier adopted as the front-end converter in power electronic transformer (PET) in high-speed train application. A two-vector-based model predictive current control (MPCC) scheme is proposed to improve controller’s dynamic responsibility and reduce current harmonic distortion. Firstly, the single phase cascaded multilevel H bridge rectifier is modeled in α-β stationary coordinate frame. Secondly, the basic vectors and the corresponding sector definition are designed for single phase cascaded multilevel rectifiers based on the space vector modulation. On the basis of this principle, the optimal dwell time of two vectors is derived from minimizing the cost function which evaluates the current error. Then, the appropriate redundancy vector is selected according to the DC-link capacitor voltage balance rule in each module. Compared with the traditional instantaneous current control (ICC) based on proportional-integral (PI) controller, the proposed MPCC scheme can achieve fast dynamic response, keep DC-link capacitor voltage balance, and be free of PI current controller as the inner loop. Finally, the proposed MPCC and the traditional PI-ICC scheme are compared and verified by hardware-in-loop (HIL) experiment platform. HIL experimental results verify the feasibility and validity of the proposed MPCC scheme.

cascaded multilevel H bridge rectifier; single phase; model predictive control; capacitor voltage balance; direct current control

2017-01-09

国家自然科学基金项目(51577160)

蒋 蔚(1993-)， 男， 四川籍， 硕士研究生， 研究方向为电力牵引交流传动及其控制；

宋文胜(1985-)， 男， 安徽籍， 副教授， 硕导， 博士， 研究方向为电力牵引交流传动及其控制(通讯作者)。

10.12067/ATEEE1701035

1003-3076(2017)11-0036-08

TM461