高炉冶炼过程的大数据建模研究

曹正盛 冯健沛 杨非 蔡俊 廖进（南昌大学 理学院，江西 南昌 330031）

高炉冶炼过程的大数据建模研究

曹正盛 冯健沛 杨非 蔡俊 廖进（南昌大学 理学院，江西 南昌 330031）

利用遗传算法优化的BP神经网络和局部线性的混沌时间序列模型对连续1000组高炉数据进行了预测。实验结果表明GA-BP神经网络相比传统BP神经网络在各方面都有了很大的提升；局部线性混沌时间序列的预测结果相当好，均高达80%以上，对实际生产有很好的指导作用。

含硅量[Si]；GA-BP神经网络；混沌时间序列；预测模型

对高炉复杂系统的建模与控制一直以来都是冶金科技发展的前沿，其中对高炉炉温的预测与控制更是难点所在[1]。本文采用GA-BP神经网络和局部线性的混沌时间序列预测模型，对含硅量[Si]进行预测。GA-BP神经网络利用遗传算法的全局搜索改进了传统BP神经网络易陷入局部最小值的问题,提高了模型的预测性能。并且神经网络的泛化能力和非线性映射能力都使模型的应用突破了传统模型的局限性，而混沌时间序列模型充分利用信息，精度较高。

1 含硅量Si的动态建模预处理

炼铁过程依时间顺序采集的工艺参数是一个高维的大数据时间序列。本文利用某高炉连续1000组正常时间生产的数据作为数学建模分析的基础。

为避免对预测造成影响，我们对样本数据进行预处理，对原始数据做异常值剔除。

第一步，剔除含硅量[Si]、含硫量[S]、喷煤量PML和鼓风量FL时间序列中的异常值，异常值的判断准则为：

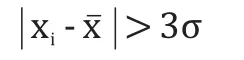
其中，σ的计算公式为：

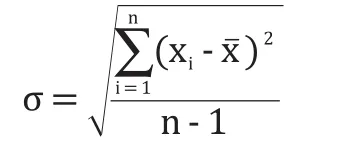
得到剔除异常值之后的 932组数据。

第二步，含硅量[Si]、含硫量[S]、喷煤量PML和鼓风量FL的量纲存在很大差异，会极大地影响后面的预测。因此我们对数据归一化至[0,1]区间，以消除这种影响。

2GA-BP神经网络预测模型

GA-BP神经网络预测模型包括：BP神经网络拓扑结构的确定、遗传算法的优化和BP神经网络的预测输出3个部分[2]。

确定BP神经网络结构主要根据输入和输出单元的个数，确定网络层的层数和节点数，进而确定遗传个体的长度。种群中的每个个体都记录了网络的所有的权值和阈值，网络每训练1次，个体就更新1次，通过适应度函数计算个体的适应度,以及利用GA算法对个体进行选择、交叉和变异。进化后的个体不断更新权值和阈值，使BP神经网络预测更加准确。

2.1 神经网络的拓扑结构及参数的确定

本文的有3个输入，1个输出。在模型训练过程中发现单隐层网络结构的效果并不很好，于是考虑双隐层结构。根据文献[3]，利用经验公式综合确定两层隐含层的单元数。

2.2 适应度函数

F为个体适应度值，k为系数，n为网络的神经元个数，yi和ai分别是预测输出和期望输出。

把训练数据预测误差的绝对值和作为个体适应度值，个体适应度值越小个体越优。

2.3 遗传操作

（1）基因选择：计算出个体适应度值，适应度越小的个体越好，被选中的概率也越高。本文选择轮盘赌法：

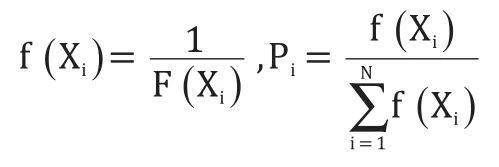
式中N为种群规模。

（2）交叉操作：交叉操作是希望通过使用交叉算子从全局考虑改善个体编码结构。个体使用实数编码，第i个染色体Xi和第j个染色体Xj在其第k位进行交叉操作的公式：

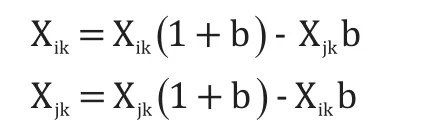
式中b为常数，取值为[ ]0,1。

（3）变异操作：为提高算法局部搜索能力及维持种群的多样性。选取第i个个体的第j个基因Xij做变异操作。则新的基因点表示为：

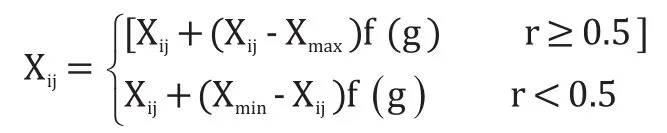
其中f(g)=r2(1-g/Gmax),Xmax和Xmin分别为初始个体基因的上界和下界，r和r2为[0,1]之间的随机数，Gmax为最大进化次数，g为当前迭代次数。

2.4 预测模型及结果

最终神经网络结构为 3-13-12-1，共有207个权值，25个阈值，所以遗传算法个体编码长度为232。932组有效数据，从中随机选择900组作为训练数据，用于BP神经网络学习，剩下32组作为测试数据。

最终得到最佳参数为：种群规模为20，进化次数为50，交叉概率为0.4，变异概率为0.2。

利用该参数重新训练模型，对含硅量[Si]预测，结果如下(见图1、图2所示)

含硅量[Si]的预测取得较好的效果：训练集的预测成功率为75.33%，测试集的预测成功率为71.88%。

相比于传统BP神经网络，笔者经过试验发现成功率不足30%，其预测性能有了一个很大的提高。当然，由于该网络模型结构较为复杂，采用了双隐层，故训练的成功率比测试的成功率略高。

图1. GA—BP神经网络训练结果

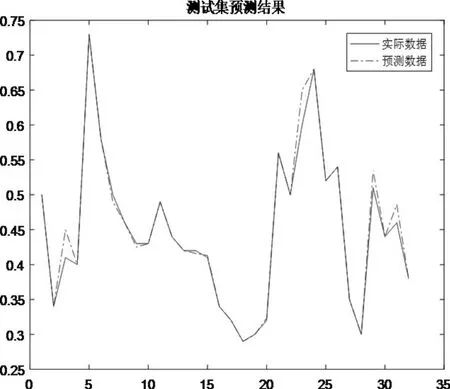
图2. GA—BP神经网络测试预测结果

3 局部线性混沌时间序列预测

对于已知的混沌时间序列{Xt},t=1,2,…,n，利用相空间重构技术和Takens定理[4]，将其嵌入到维数为 d、时滞为τ的状态空间中，重构相空间中的矢量点则可表示为：

Xt=(xt,xt+τ,…,xt+(d-1)τ)T

设预测步长为T，由Takens定理可建立混沌时间序列的预测模型为

Xt+T=f(Xt)

局部线性预测模型就是用线性多项式拟合预测器f，表示为

Xt+T=aXt+b I

式中，a，b∈R1为拟合系数，I∈Rd为各分量均为1的 d维列向量，R为实数域。

给定高炉的混沌时间序列 Xp，在重构相空间的矢量点中，选取适当的邻域半径 ε，找到邻近 Xp的 k个矢量点，

Xp1,Xp2

,…,Xpk,使满足：

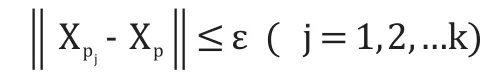
定义：

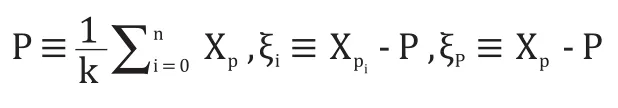
同样对 k个矢量点的 T步迭代点 Xp1+T,Xp2+T,…,Xpk+T定义：

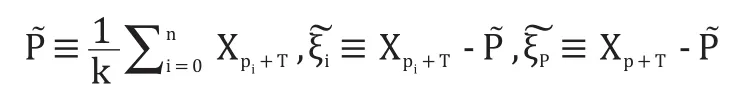
由混沌局部线性理论拟合这k个矢量点求差后的迭代规律，即使得

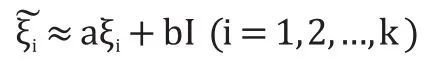
利用最小二乘法拟合系数 a,b得：

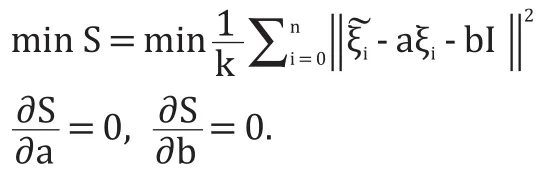
于是解得

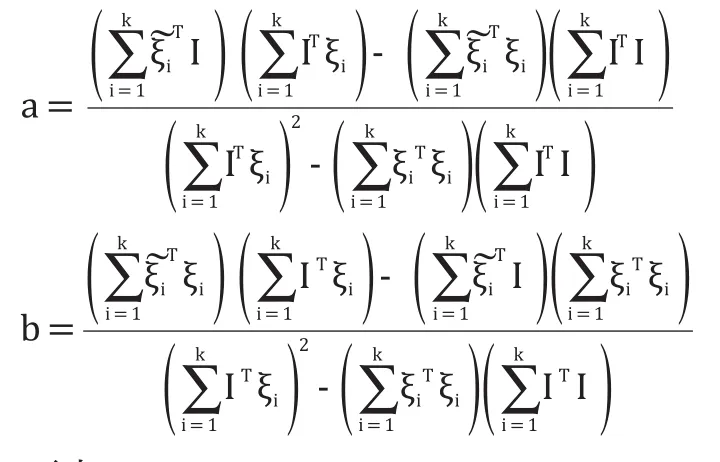
再由

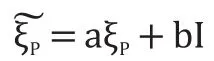
混沌时间序列模型中的线性拟合仅限于Xp的ε邻域，相当于用分段线性函数来拟合全局函数，因此整体效果仍是非线性的，故不失一般性[4]。

根据混沌分析结果[5]，对高炉冶炼过程进行了重构，经试验得到了最佳参数：

步长 T为1时，嵌入维度 d=6，滞后时间 τ=8，邻域半径 ε=0.33；步长 T为1时，嵌入维度 d=6，滞后时间 τ=7，邻域半径 ε=0.347。

混沌时间序列一步预测和两步预测含硅量[Si]的结果如下图所示，可以看出，预测数据分布在Xpi+T=X'pi+T附近，除了少部分点外，预测值与实际值基本一致。通过计算得到预测命中率在[]

Si±0.1% 分别为86.67%、83.34%，一步预测和两步预测结果如下：

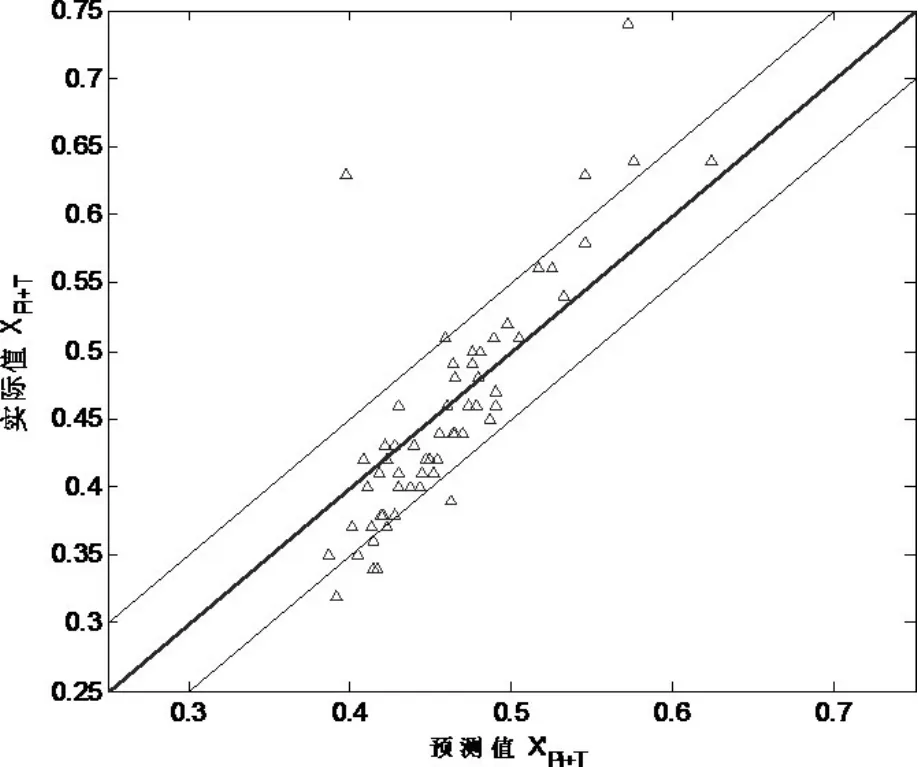
图3. 混沌时间序列一步预测结果

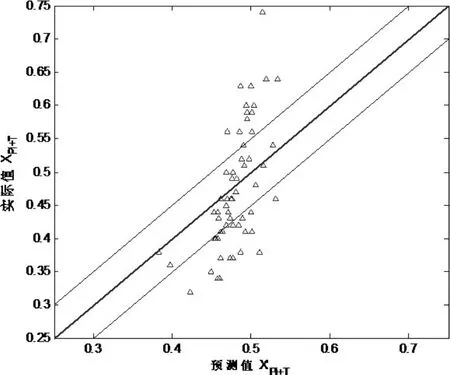
图4. 混沌时间序列两步预测结果

并且通过下面公式计算预测的精度：

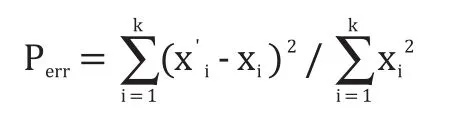
最终得到预测的结果：一步预测成功率为86.67%，精度为0.0123；二步预测成功率为83.34%，精度为0.0252。

由此可见，二步预测略差于一步预测，说明做预测时信息会逐渐的衰退、消减。除此之外，一、二步预测的精度都控制在10-2数量级，符合高炉冶炼的工艺要求，对生产有较好的指导作用。

4 结语

GA-BP神经网络模型和混沌时间序列模型预测含硅量[Si]都取得了不错的效果。相比之下，混沌时间序列相比较而言更好，原因是时间序列将滞后考虑在内，即将前几炉含硅量[Si]所包含的信息也考虑在内。

而且混沌时间序列的预测成功率都在80%以上而一步预测成功率在[Si]±0.1%更高达86.67%，这在国内也是十分少见的，对于我国中小型炉的冶炼过程和实际生产具有良好的指导意义。

另外，GA-BP神经网络虽然预测结果不错，但它的网络结构过于复杂，虽然笔者在训练时已经注意避免了过训练或过拟合的情况，但是不可避免还是会有一些影响，因而如何精简网络的拓扑结构是将来的主要工作之一；其次局部线性混沌时间序列邻域半径 ε的选取具有主观性，而ε的值对于预测的影响很大，所以需要我们经过反复试验才能得到，仍需进一步改进。

[1]Committee of National Natural Science Foundation of China. Automatic Science and Technology— The Re⁃search Report on Development Stratagem of Natural Science Subject.Bejing：Science Press,1995:132（国家自然科学基金委员会,自动化科学与技术 —自然科学学科发展战略调研报告.北京：科学出版社，1995:132）

[2]刘奕君,赵强,郝文利.基于遗传算法优化BP神经网络的瓦斯浓度预测研究[J].矿业安全与环保，2015,42(2):56-60.

[3]沈花玉,王兆霞.BP神经网络隐含层单元数的确定[J].天津理工大学学报,2008,24(5):13-15

[4]郜传厚,刘祥官.高炉冶炼过程的混沌性辨识Ⅰ.饱和关联维数的确定[J].金属学报,2004,40(4):347-350

[5]郜传厚,周志敏.高炉铁水的含硅量混沌局部线性预测[J].金属学报,2005,41(4):433-436