奥运会奖牌榜影响因素的数学分析①

朱梦楠 彭涛 陈轲

(江苏大学能源与动力工程学院 江苏镇江 212013)

奥运会奖牌榜影响因素的数学分析①

朱梦楠 彭涛 陈轲

(江苏大学能源与动力工程学院 江苏镇江 212013)

利用第26～31届夏季奥运会奖牌榜排名前10位国家的相关数据，使用多元线性回归法建立了奥运会奖牌榜排名在影响因素：国家综合实力、人口数量、国家体制和东道主效应作用下的线性回归方程。运用基于GM（1,1）模型的灰色预测，利用前6届国家影响奖牌榜排名相关数据，预测出了2020年相应影响因素对应的数值，采用加权求和和定量计算的方式预测了2020年东京奥运会的奖牌榜前10名的排名。

奖牌榜排名 影响因素 多元线性回归 灰色预测

2016年里约奥运会已经落下帷幕，中国代表队取得了金牌榜第三，奖牌榜第二的好成绩。2020年东京奥运在即，一旦比赛敲响，一切准备与喧哗都将化为赛场上的真实较量。哪个国家将在本次奥运会上争夺最多的奖牌？哪个国家的国歌将最频繁地在奥运领奖台上响起？这些问题也成为人们期待中的热点[1]。一个国家所获得的奖牌数不仅仅受到运动员竞技水平单一要素的影响，更受到国家经济实力、人口数量、政治结构等多因素的影响。对于奥运会奖牌榜排名的影响因素，已经有学者开始相关的研究工作。但是相关文献研究大多只进行定性分析，而不进行定量分析。在定量分析的研究中，存在着相关影响因素少、分析方法单一的问题。本文在借鉴以前相关研究的基础上，通过多元线性回归模型，建立了2020年东京奥运会奖牌榜排名预测的数学模型。影响2020年东京奥运会的因素有国家综合实力、人口数量、政治体制和东道主组成，本文分别选用人均GDP，人口规模等级，同时将政治体制和东道主用虚拟变量1，0表示，分别作为相应因素的指标，采用加权求和和定量计算的方式预测了2020年东京奥运会的奖牌榜排名。

1 影响因素分析及数学模型建立、分析

1.1 影响因素分析

预测奥运会的奖牌榜排名这一问题，本质上为统计学问题，即运用一些基于客观变量的数学模型对奥运比赛进行预测，问题的关键在于找到各个影响因素对于获得奖牌事件影响作用的大小。影响奖牌榜排名的因素分为国家综合实力、人口、政治环境、举办地四个指标，分别以人均GDP，人口规模等级，政治体制以及东道主效应作为反映以上4点影响因素的指标。这4个指标的影响系数分别为人均GDP对奖牌榜的影响系数β1，人口总量对奖牌榜的影响系数β2，政治环境对奖牌榜的影响系数β3，东道主对奖牌榜的影响系数β4。

总的说来，国家的综合实力E是否雄厚，决定这个国家对体育事业资金投入的多少。如果各个国家各种人才的概率分布是相同的，那么在其他条件相同的情况下，人口规模等级P大的国家将拥有绝对数量更多的优秀运动员，大大提高一个国家在奥运会得奖的概率。人口规模与等级的关系见表1所示。国家性质决定政府职能，政府制定什么样的政策取决于一个国家用的是什么样的体制。这里把国家体制G作为政府政策的主要影响因素。而国家体制G是指一个国家采取的社会制度，主要分为社会主义国家和资本主义国家两类。通常社会主义国家的中央政府比资本主义国家有更高的号召力和对全国资源的整合能力。这里把国家体制G作为虚拟变量，取值0或1，1表示社会主义，0表示资本主义。东道主H拥有主场优势的同时，本国运动员对本国的气候、食物等条件比外国运动员更加适应[2]，这里东道主效应H为虚拟变量，取值0或1，1表示有东道主效应，0表示无东道主效应。

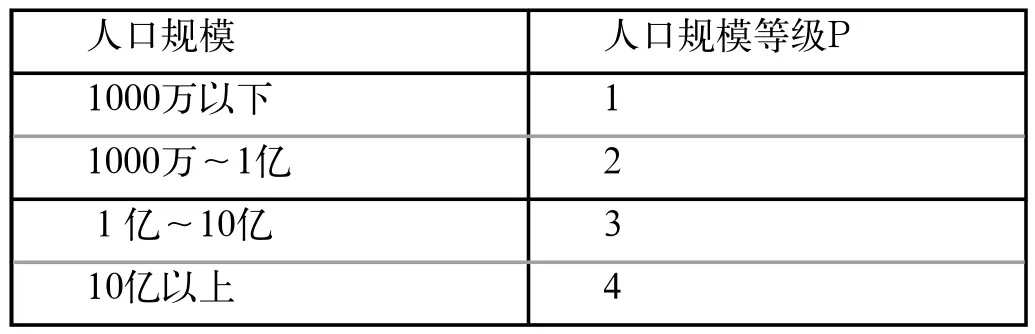
表1 人口规模与等级的关系

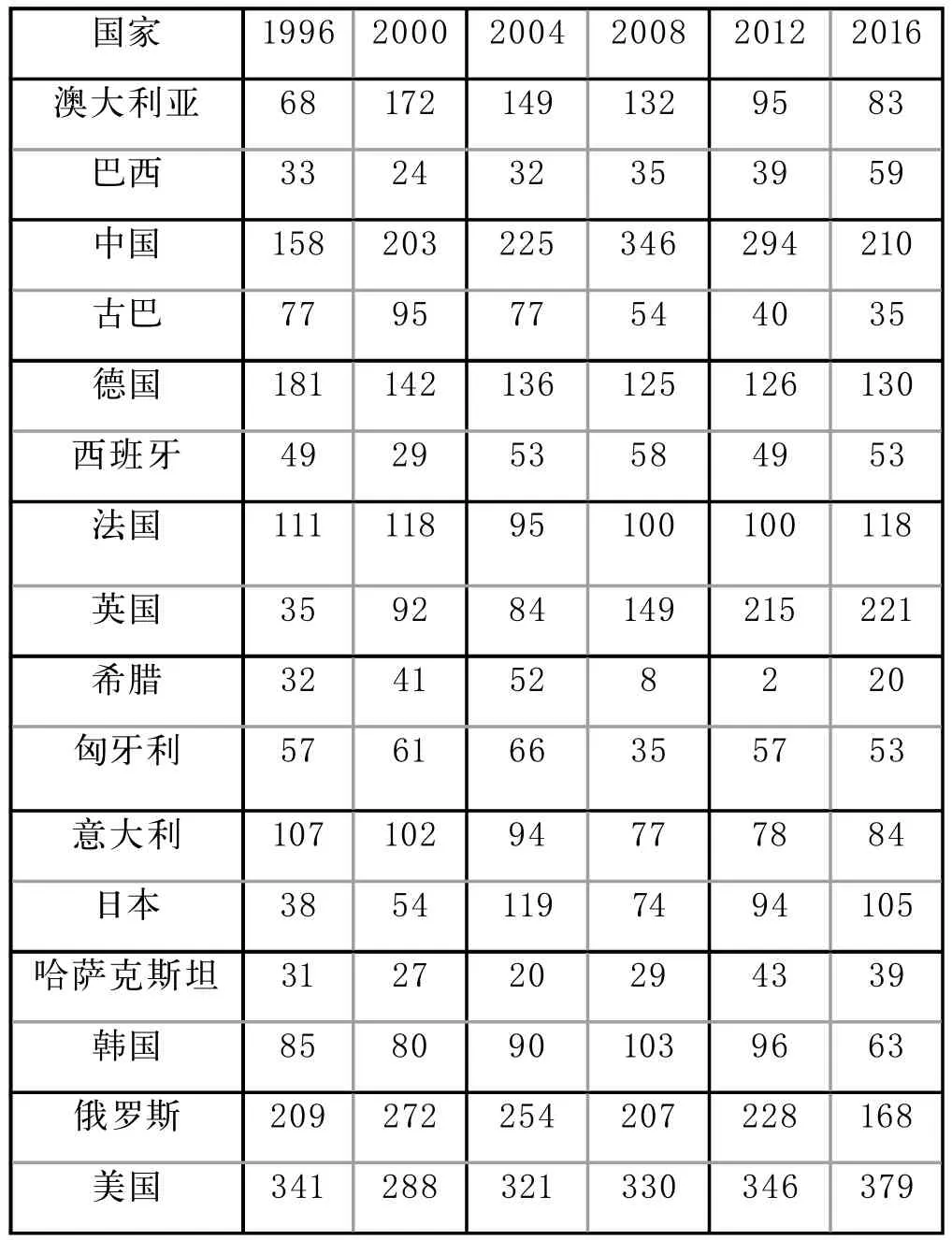
表2 6届奖牌榜前10名国家奖牌榜影响因素加权值

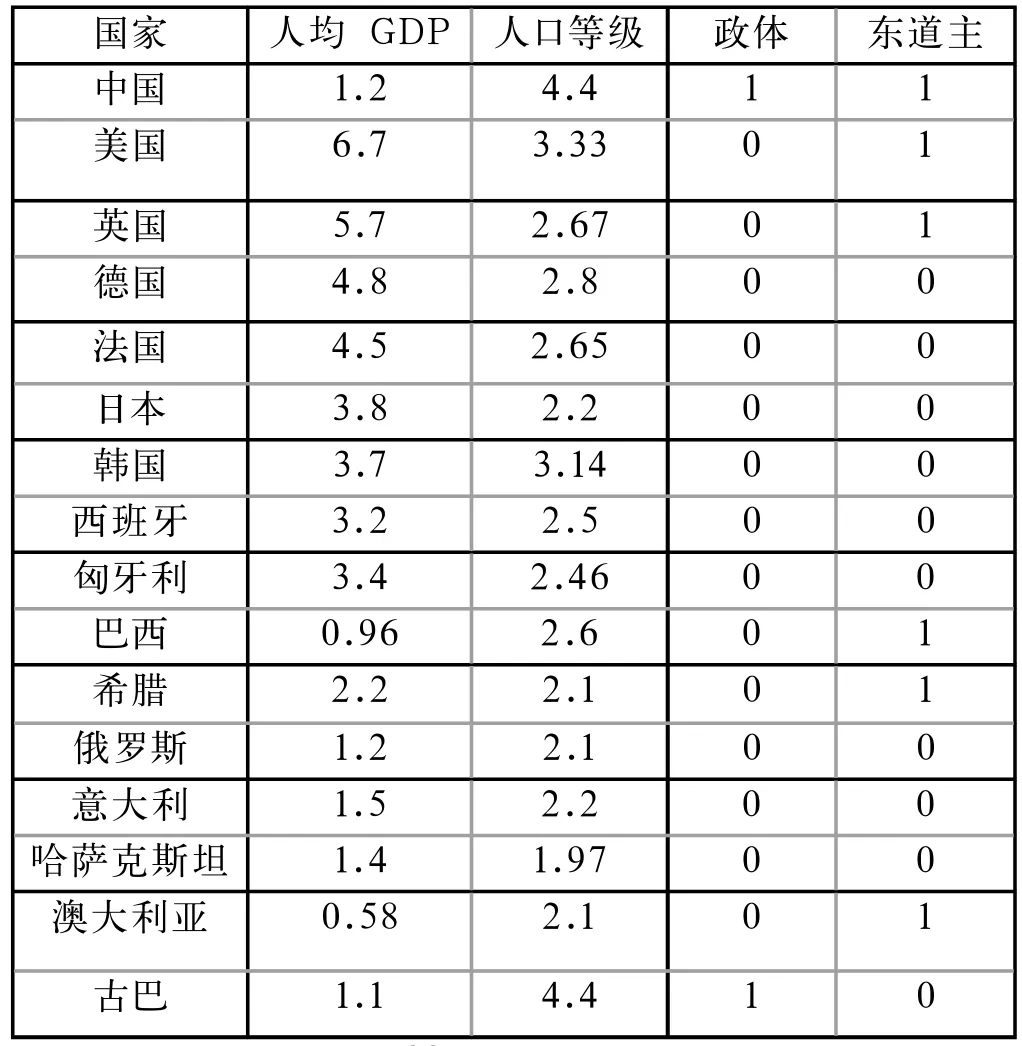
表3 2020年奖牌榜排名影响因素预测值

1.2 模型的建立、分析

1.2.1 模型的建立

利用奖牌积分作为奖牌榜排名确定的依据，其中奖牌积分计算方法为：Y=金牌数×5+银牌数×3+铜牌数×1（即金牌权重为5分，银牌权重为3分，铜牌的权重为1分）。

一般而言，设系统变量y与k个自变量x1，x2…xk之间存在统计线性相关关系，且给定n组样本数据点如下：

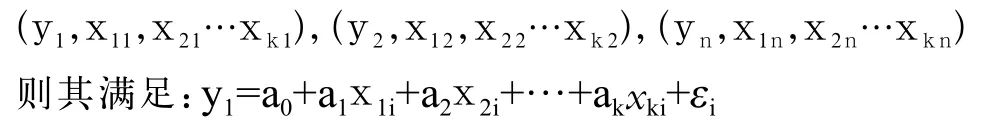
多元线性回归模型可以表示为：

解上面的方程组即可得到a0，a1，…，ak的估计值，系统值奖牌榜排名Y即是在4个自变量：人均GDP、人口规模等级、政治体制以及东道主效应作用下的线性回归问题。可以认为每届奥运会获得奖牌榜前10名的国家基本不变，即可以认为每届奥运会奖牌榜的前10名从以前得过奥运会奖牌榜前10名的国家中产生。这种假设符合实际情况的同时，减少了数据收集和分析的工作量。收集1996—2016年得过奥运会奖牌榜前10名的16个国家的人均GDP、人口规模等级、政治体制以及东道主效应，按照奖牌榜积分值计算方法得到表2的数据。

利用MATLAB中regress多元线性回归分析得到的结果为：Y=-201.2233+23.5087×E+96.5315×P+33.3057×G+1.0899×H。

1.2.2 灰色预测

灰色预测模型是通过少量的、不完全的信息，建立数学模型并做出预测的一种预测方法。当我们应用运筹学的思想方法解决实际问题，制定发展战略和政策、进行重大问题的决策时，都必须对未来进行科学的预测。预测是根据客观事物的过去和现在的发展规律，借助于科学的方法对其未来的发展趋势和状况进行描述和分析，并形成科学的假设和判断。所以，基于我们收集到的有限的数据，我们利用灰色预测模型，分别预测出2020年的参赛国家的人均GDP以及人口数量的变化。灰色预测的一般步骤如下文所示：

表4 2020年东京奥运会奖牌榜预测排名

表5 模型综述

表6 参数估计值

在此我们依据x(0)数据建立GM（1，1）实现预测功能，具体步骤如此下：记x(1)为生成数列：

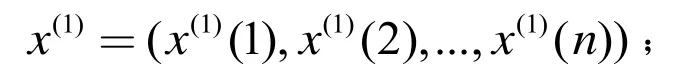
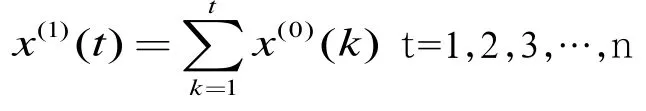
对x(1)(t)建立x(1)(t)的一阶线性微分方程：

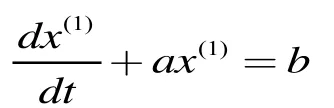
其中a，b为待定系数，分别为发展系数和灰色作用量，a的区间为（-2，2），记a，b组成的矩阵为求出参数a，b，就能求出进而求出的预测值。

对累加生成数据做均值生成B与常数项向量yn，即：

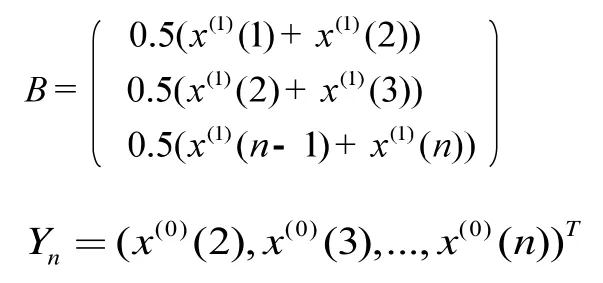
用最小二乘法，通过最小误差的平方和寻找数据函数的最佳匹配求解灰参数a'：

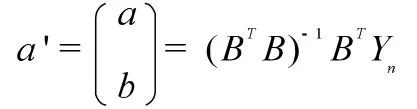
将灰色参数a'代入进行求解，得：

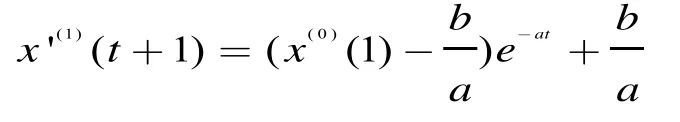
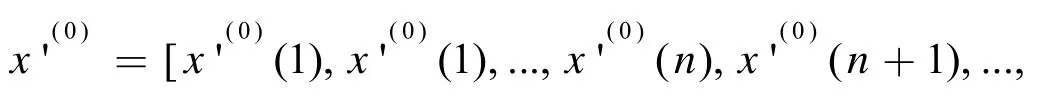
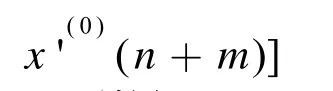
利用MATLAB软件实现GM(1，1)灰色预测，得出2020年16个相关国家的影响奥运会奖牌榜排名因素的权值，见表3。

根据多元线性回归表达式：

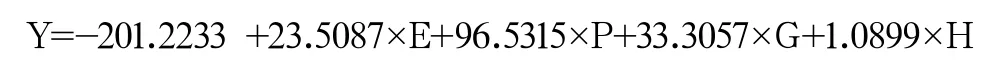
可得，2020年各个国家的奖牌榜排名见表4。

从模型可得2020年东京奥运会的奖牌榜前10名预测结果为：中国、美国、英国、日本、德国、法国、澳大利亚、俄罗斯、韩国、西班牙。

1.2.3 模型的分析

模型的回归系数分析见表5。

F分布的显著性概率为0，即检验假设“H0：回归系数B=0”成立的概率为0，从而拒绝0假设，说明因变量与自变量的线性关系是显著的，可建立线性模型，见表6。

复相关系数检验如下：

y的每次取值yk（k=1，2，3…）是有波动的，这种波动称为变差。每次观测值yk的变差大小常用该次观测值与n次观测值的平均值的差来表示，称为离差，而全部观测值的总变差可由总的离差的平方和用Syy表示。

Q称为剩余平方和(或称残差平方和)，是实测值yk与回归值之差的平方和，它是由试验误差及其他因素引起的，其自由度fQ=n-m-1（n为数据个数，该线性回归数据个数为16个，m为自变量个数，为4个），

引入无量纲指标复相关系数R（0＜R＜1）作为检验总的回归效果的指标，回归平方和U实际上是反映回归方程中全部自变量的“方差贡献”，因此R就是这种贡献在总回归平方和中所占的比例，因此R表示全部自变量与因变量y的相关程度。复相关系数越接近1，回归效果就越好。记Ra为临界复相关系数，

当R＞Ra时，称线性回归方程显著，则在4个影响因素作用下的奥运会奖牌榜排名积分线性回归方程显著。

F检验分析如下：

要检验y与x1，x2…是否存在线性关系， 就是要检验假设H0：β1=β2=……=0。

当假设H0成立时，则无线性关系，否则认为线性关系显著。所以应该拒绝假设H0。检验假设H0应用统计量这是两个方差之比，它服从自由度为m及n-m-1的F分布，即

用此统计量可检验回归的总体效果。如果假设成立，则当给定检验水平α=0.01下，统计量F应有对于给定的置信度α=0.01，由F分布表可查得的值，如果根据统计量算得的值为则拒绝假设H0， 即不能认为全部βi为0，即m个自变量的总体回归效果是显著的， 否则认为回归效果不显著。查表可得，则，则F检验通过。

2 结论

利用多元线性回归方法得出了在国家综合实力、人口数量、国家体制和东道主效应4个影响因素作用下的奥运会奖牌榜积分的线性回归方程，使用灰色预测克服了数据少且规律性不强的特点[3]，预测得出了2020年东京奥运会的奖牌榜积分前10名的国家为：中国、美国、英国、日本、德国、法国、澳大利亚、俄罗斯、韩国、西班牙。综合以上分析，可以得出以下几点结论。

(1)对回归系数进行检验，利用复相关系数检验和F检验，说明基于多元线性回归方法得出的回归方程具备合理性和科学性。采用多元线性回归的方法，将复杂的问题分解成能够被量化分析的简单问题。

(2)上述所建立的模型具有一定的推广性，可用于以后多届奥运会的结果。

(3)除了上述文中已经考虑到的因素，还有其他因素可能影响最终的结果。日后的研究中，可将更多的因素考虑进去，做出更合理、有效地预测。

[1]王雅平.国家之间的体育角逐？——经济学家运用经济模式预测各国奥运奖牌总数[EB/OL].http：//carnegieendowment.org/2008/07/01/zhpub-47475.2017.5.14.

[2]王宇鹏，许健，张媛媛.奥运会奖牌榜影响因素的实证分析[J].统计研究，2008，25（10）：138-139.

[3]王道林，樊新生.奥运金牌数预测的灰色模型[J].山东体育科技，2005，27（2）：45.

Use the 5 Olympic Games medal table data since the 26th Olympic Game and the multiple linear regression to establish the linear regression equation, based on the relevant factors: national comprehensive strength, population, state system and effects of the host. Based the grey forecasting model, predict the relevant data influencing the medal table. Use the weighted sum and quantitative calculate and forecast the result of the Tokyo Olympic Game medal table.

Olympic medals；Factors；Multiple linear regression；Grey forecasting model

G812

A

2095-2813(2017)09(c)-0239-05

10.16655/j.cnki.2095-2813.2017.27.239

朱梦楠(1995，9—)，男，汉族，江苏徐州人，本科，研究方向：流体机械，计算机应用。