理解DFT如何逼近FT的实例教学法

徐友根， 彭开南， 郑一鸣

(北京理工大学 信息与电子学院， 北京 100081)

理解DFT如何逼近FT的实例教学法

徐友根， 彭开南， 郑一鸣

(北京理工大学 信息与电子学院， 北京 100081)

本文结合一个离散傅里叶变换DFT计算实例，分析了DFT与连续时间傅里叶变换FT之间的联系，以较为直观的方式阐述了由FT到DFT的演变过程，以及该过程关键环节对最终结果的影响，主要包括谱泄漏，折叠效应，栅栏效应以及谱折移等。教学实践表明，通过该实例讲述DFT对FT的逼近问题，能有效加深学生对DFT的认识和理解。

数字信号处理；傅里叶变换；离散傅里叶变换

0 引言

离散傅里叶变换DFT作为有限长序列的一种频域表示法，在理论上有着重要的作用。由于其存在快速计算方法—快速傅里叶变换FFT，因而在数字信号处理中也有着重要的作用。

现有数字信号处理教材在引入DFT概念时，一般从连续非周期信号的傅立叶变换FT出发，将信号时域采样，从而FT转化为离散时间傅里叶变换DTFT。然后将信号的频谱采样，得到离散傅立叶级数DFS的公式。再将时域和频域上各取一个主值区间就形成了DFT。这一过程中存在四种变化需要注意，也即截断效应(谱泄漏)，折叠效应，栅栏效应以及谱折移[1,2]。根据笔者的教学体会，很多学生虽然应用DFT公式计算相当熟练，但对DFT概念的来龙去脉未必清楚，对上述四种变化引出的误差也缺乏直观认识。

本文通过DFT计算实例，对由FT到DFT的演变过程作了简单而系统的阐述，将其引入到教学中，讲授DFT对FT的逼近问题能加深学生对DFT概念的理解和掌握。

1 DFT逼近FT的过程

图1所示为DFT逼近FT的详细过程。

2 DFT计算

考虑下述DFT计算实例：

对模拟信号xa(t)=-0.5+cos2(200πt)以一定的采样率进行采样，得到一个 256点数字序列，记作x(n)，其中n=0～255。

图1 DFT逼近FT的过程

若采样率为Fs=0.8 kHz，计算序列x(n)的256点DFT。

对于该实例，如果直接利用公式求取DFT，结果为

DFT[x(n)]=64[δ(k-64)+δ(k-192)]

(1)

式中，δ(·)表示狄拉克Delta函数,k=0～255。

上述计算过程十分简单，但是直接公式计算的方法无法体现出如图1所示的由DFT逼近FT的详细过程。本节探讨上述实例的另一种解法，借此分析由DFT逼近FT的全过程。

2.1信号数字化前后的时域变化

首先，根据题意可知时域采样后的离散信号为x(n)=0.5cos(400πn/Fs)，其中n=0～255。故此，采样区间应为0～255/Fss，而记录长度则为tp=256/Fs=0.32 s。这一采样截断过程也等效于先将原信号xa(t)加窗截断为x(t)再采样，其中窗函数w(t)长度为tp，如图2所示。

由于xa(t)的周期为T=0.005 s，也即采样间隔为1/Fs=0.00125 s，故此采样的完整周期数应是tp/T=64，由此可知，一个周期内的采样点数为FsT=Fs/200=4，如图2所示。

2.2信号数字化前后的频谱变化

根据定义，不难得到原周期余弦信号xa(t)的频谱为Xa(f)=0.5π[δ(f-200)+δ(f+200)]。由卷积定理可知，截断信号x(t)的频谱应为Xa(f)与窗函数频谱W(f)的卷积，其中

W(f)=tpsinc(ftp)e-j2πftp/2

=0.32sinc(0.32f)e-j0.32πf

(2)

图2 信号数字化前后时域关系示意图

式中，sinc(·)表示辛格函数。根据辛格函数的性质，函数零点位于f=n/tp处，其中n为非零整数。再注意到tp=256/Fs，也即1/tp=Fs/256，所以W(f)的零点间隔刚好应该为DFT频率分辨率Fs/256的整数倍，如图3所示。

根据定义，W(f)与Xa(f)卷积后的结果为

(3)

卷积之后的频谱零点仍位于f=n/tp处，其中f≠±200 Hz。

对x(t)采样后，所得信号xs(t)其频谱将以采样率Fs=0.8 KHz为周期进行周期延拓，同时谱值变为原来的Fs倍，即tpFs/4=64，如图3所示。

对上述频谱进行采样，主值区间值即为x(n)的DFT结果。根据DFT的定义，其主值区间内频谱采样点数为256。又由于DFT的频率分辨率为Fs/256，所以采样点应位于f=kFs/256处，其中k=0～255。当k在0～255这一范围内取值时，由于频谱零点位于f=n/tp=nFs/256处，其中f≠(±200+800m)Hz，m为任意整数。故此，只有在f=200 Hz和f=600 Hz，也即k=64和k=192时，采样结果不为0，其他点全部对应着频谱的零点，如图3所示，此DFT结果与式(1)所示结果完全相同。

3 结果辨析

上述DFT计算结果中仅有两根谱线，似乎很接近FT频谱，但两者具有明显区别。

(徐友根等文)

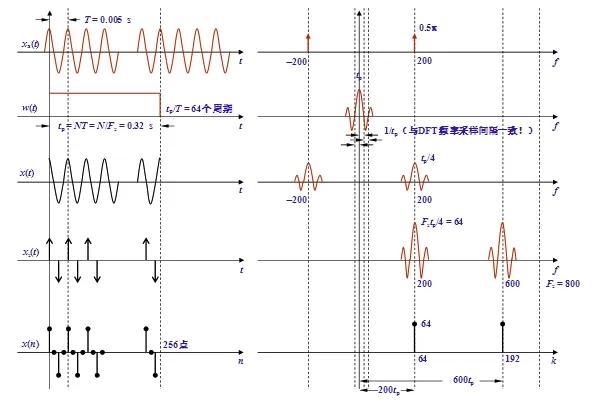
图3 信号数字化前后频谱关系示意图

事实上，无论时域采样率多高，DFT逼近的仅是截断采样信号xs(t)的FT主值区间内容，或者序列x(n)的DTFT的主值区间内容，这一过程存在谱泄露，折叠效应，栅栏效应以及谱折移等几点问题需要注意。

本例中的采样为整周期采样，采样点刚好位于辛格函数的零点处，DFT的结果只含有两条谱线，但由第2.2节中的讨论可知，该两根谱线位置取决于频率分辨率。

现800×64/256=200 Hz，位置相同。离散信号频谱幅度与连续信号频谱积分幅度之间的关系与信号的时域离散化、加窗(频谱卷积)等有关。另外，本例中是存在谱泄露现象的，但由于栅栏效应而并未被观察到。

若采用非整周期采样的方法，使频率采样点避开辛格函数的零点，即可观察到栅栏效应，计算机仿真结果如图4所示，通过对比，可以看出非整周期采样使DFT的结果更加逼近截断采样信号xs(t)的FT，或者说更逼近x(n)的DTFT主值区间内容。当然，采用补零的方法也可减小栅栏效应，但其与非周期采样结果的实质并不完全相同，具体如图4所示。

图4 整周期采样和非整周期采样DFT的比较

4 结语

通过本文列举的一个DFT计算实例，可以清楚地阐述DFT对FT的逼近过程，及其中所存在的四种主要变化。笔者在讲授数字信号处理DFT部分时，采用了上述实例法，起到了很好的教学效果。实践表明，采用该法，使学生很易理解和掌握DFT基本概念，一定程度上跳出了仅注重表面公式计算而忽视其内涵和实质的误区。

[1] 程佩青. 数字信号处理教程[M]. 北京: 清华大学出版社, 2013年2月.

[2] 赵春晖, 乔玉龙, 崔颖. 数字信号处理学习指导及实验[M]. 北京: 电子工业出版社, 2008年10月.

AnExample-BasedIllustrationoftheConnectionbetweenDFTandFT

XUYou-gen,PENGKai-nan,ZHENGYi-ming

(SchoolofInformationandElectronics,BeijingInstituteofTechnology,Beijing100081,China)

The connection relationship between the discrete Fourier transform (DFT) and the continuous time Fourier transform (FT) is analyzed in this paper based on an example. The main contents of the relationship are spectral leakage, aliasing problem, grating phenomenon, and spectral shift. Teaching practice shows that this example-based method is very helpful for student to understand how DFT works.

digital signal processing; Fourier transform; discrete Fourier transform

2016-10-18;

2017-02-16

徐友根(1975-)，男，博士，教授，主要从事数字信号处理方面的教学与科研工作，E-mail: yougenxu@bit.edu.cn

TN913

A

1008-0686(2017)05-0076-03