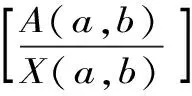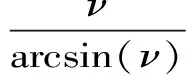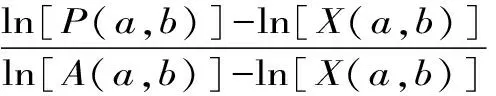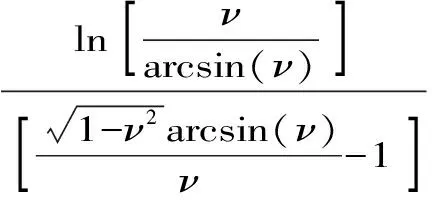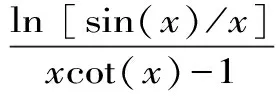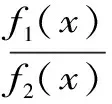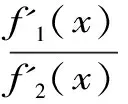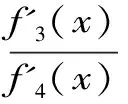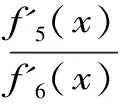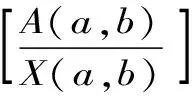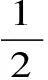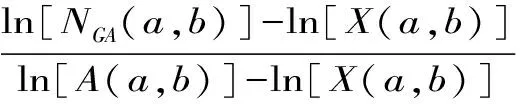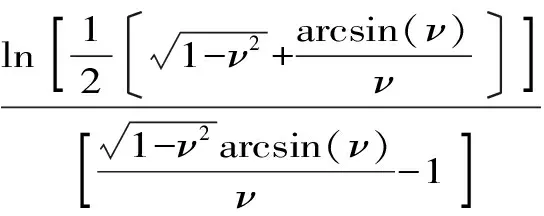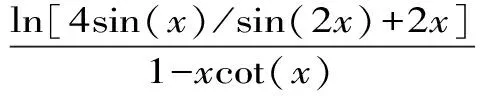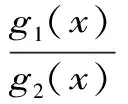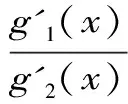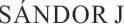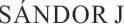两个涉及Seiffert和Neuman平均的双向不等式
沈林昌, 王君丽
(1.湖州善琏成人文化学校, 浙江 湖州 313000; 2.台州科技职业学院 成人教育学院, 浙江 台州 318020)
两个涉及Seiffert和Neuman平均的双向不等式
沈林昌1, 王君丽2
(1.湖州善琏成人文化学校, 浙江 湖州 313000; 2.台州科技职业学院 成人教育学院, 浙江 台州 318020)
应用实分析的方法,找到了最佳参数α1,α2,β1,β2∈(0,1)使得双向不等式:
Aα1(a,b)X1-α1(a,b) Aα2(a,b)X1-α2(a,b) 对所有a,b>0和a≠b成立。其中P(a,b),NGA(a,b),X(a,b)和A(a,b)分别表示两个正数a和b的第一类Seiffert平均,Neuman平均,Sándor平均和算术平均。 第一类Seiffert平均; Neuman平均; Sándor平均; 算术平均; 不等式 Aα1(a,b)X1-α1(a,b) Aα2(a,b)X1-α2(a,b) 对于a,b>0和a≠b,第一类Seiffert平均P(a,b)[1]253-266 [2]49-59,Neuman平均NGA(a,b)[3]277-289,Sándor平均X(a,b)[4]409-413和调和平均H(a,b)、几何平均G(a,b)、算术平均A(a,b)和p阶幂平均Mp(a,b)分别定义如下: (1) (2) (3) H(a,b) =M-1(a,b) 一直以来,第一类Seiffert平均P(a,b)、Neuman平均NGA(a,b)和Sándor平均X(a,b)与其他各种二元平均组合的比较研究吸引了许多学者的注意。 Seiffert[5]195-198证明了 对所有a,b>0和a≠b成立。 褚玉明等[6] [7]发现了最大值α1,α2和最小值β1,β2使得双向不等式 对所有a,b>0和a≠b成立。 在文献[3]277-289,Neuman证明了双向不等式 αA(a,b) +(1-α)G(a,b) 对所有a,b>0 和a≠b成立,当且仅当a≤2/3和β≥π/4。 Sándor[8]1-9证明了如下不等式: 推荐理由:作者曾获以色列布伦纳奖、以色列总理奖、美国犹太图书奖等奖项,这部小说被他视为自己创作成熟的标志。中文译本首次出版。小说讲述了1930年代巴勒斯坦的一个小村庄里,朱迪斯与她的三个爱慕者之间发生的故事。作者从宗教故事和神话传说中汲取灵感,并融入犹太乡村的风土人情,用魔幻现实主义的高超技法,将这个《雅歌》般的传奇娓娓道来。 对所有a,b>0和a≠b成立。 杨镇杭[9]证明了双向不等式: 对所有a,b>0 和a≠b成立。 本文的主要目的是给出最佳参数α1,α2,β1,β2∈(0,1)使得双向不等式: Aα1(a,b)X1-α1(a,b) 对所有a,b>0和a≠b成立。 为了证明本文主要结果,需要以下引理2.1。 引理2.1 对于-∞ 定理2.2 双向不等式: Aα1(a,b)X1-α1(a,b) (4) 对所有a,b>0和a≠成立,当且仅当α1≤1/2和β1≥1- ln (π/2)=0.548 4L。 证明:双向不等式(4)可以写成如下形式: (5) 从二元平均P(a,b),X(a,b) 和A(a,b)是对称和一阶齐次的,不妨假设a>b>0。设ν=(a-b)/(a+b)∈(0,1),则从等式(1)和(3)式导致: (6) 根据等式(6),不等式(5)等价于: (7) 设x=arcsin(ν)∈(0,π/2)。则简单计算可得: (8) 其中 (9) 设f1(x)=ln[sin(x)/x],f2(x)=xcot(x)-1,f3(x)=xsin(2x)-2sin2(x),f4(x)=xsin(2x)-2x2,f5(x)=2xcos(2x)-sin(2x),f6(x)=sin(2x)+2xcos(2x)-4x。那么,简单计算导致: (10) (11) (12) (13) 不难证明,函数x→tan(x)/x在(0,π/2)是严格单调上升且值域为(1,+∞),从而等式(13)导致的结果是f'5(x)/f'6(x)在(0,π/2)是严格单调下降;那么,从引理2.1和等式(10)-(12)协同f'5(x)/f'6(x)的单调性,就可以清楚地看到函数f(x)在(0,π/2)是严格单调下降的。注意到: (14) (15) 所以,容易从不等式(5),(7)和等式(8),(9),(14),(15)协同函数f(x)的单调性得到定理2.2。 定理2.3 双向不等式: Aα2(a,b)X1-α2(a,b) (16) 对所有a,b>0和a≠b成立,当且仅当α2≤1/2和β2≥1+ln(4/π)=0.758 4L。 证明:双向不等式(16)能够表达成如下形式 (17) (18) 设x=arcsin(ν) ∈(0,π/2)。则简单计算可得: (19) 其中 (20) 设g1(x)= ln[4sin(x)/sin(2x)+2x],g2(x)=1-xcot(x)。那么,简单计算导致: (21) (22) 不难证明函数x→x/sin(x)在(0,π)是严格单调上升,从而等式(22)导致的结果是g'1(x)/g'2(x)在(0,π/2)是严格单调下降;那么,从引理2.1和等式(21)协同g'1(x)/g'2(x)的单调性,可以清楚地看到函数g(x)在(0,π/2)是严格单调下降。注意到: (23) (24) 所以,容易从不等式(17),(18)和等式(19),(20),(23),(24)协同函数g(x)的单调性得到定理2.3。 [3] NEUMAM E.On a new bivariate mean,Aequationes[J].Mathematicac,2014(3). [6] CHU Y M,QIU Y F,WANG M K,etc.The optimal convex combination bounds ofarithmetic and harmonic means for the Seiffert’s mean[J].Journal of Inequalities and Applications,Article ID 436457,7 pages,2010. [7] CHU Y M,QIAN W M,WU L M,etc.Optimal bounds for the first and secondSeiffert means in terms of geometric,arithmetic and contra-harmonic means[J].Journal of Inequalities and Applications,2015(44). [9] YANG Z H,WU L M and CHU Y M.Sharp power mean bounds for Sándor mean[J].Abstract and Applied Analysis,Article ID 172867,5 pages,2014. [10] ANDERSON G D,VAMANAMURTHY M K and VUORINEN M.K.Conformal Invariants,Inequalities,and Quasiconformal Maps, Canadian Mathematical Society Series of Monographs and Advanced Texts[J].New York:John Wiley & Sons,1997. TwotheDoubleInequalitiesInvolvingSeiffertandNeumanMeans SHEN Lin-chang1, WANG Jun-li2 (1.Huzhou Shanlian Adult School, Huzhou 313000, China;2.School of Adult Education, Taizhou Vocational College of Science & Technology, Taizhou 318020, China ) In this paper, we apply the method of real analysisand and find the best possible parameterα1,α2,β1,β2∈(0,1) such that the double inequalities: hold for alla,b>0 anda≠b, whereP(a,b),NGA(a,b),X(a,b)andA(a,b) are the fires Seiffert, Neuman, Sándor and arithmetic means of two positive numbersaandb, respectively. first Seiffert mean; Neuman mean; Sándor mean; arithmetic mean; inequalities 2016-12-08 1.沈林昌(1961-),男,浙江湖州人,中学一级,主要从事解析不等式研究;2.王君丽(1972-),女,浙江台州人,副教授,主要从事凸函数与解析不等式研究。 O151.23 A 1672-2388(2017)03-0074-04一、前 言
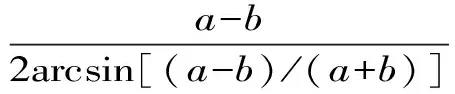
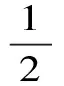

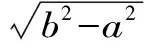
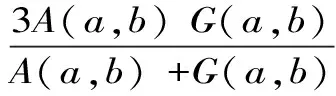
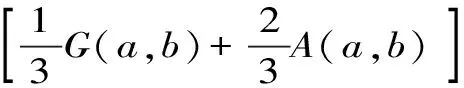
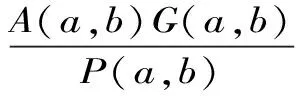
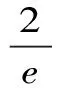
二、主要结果