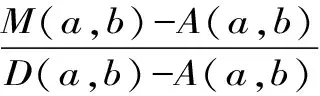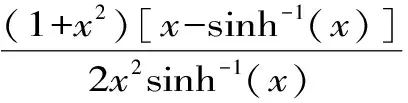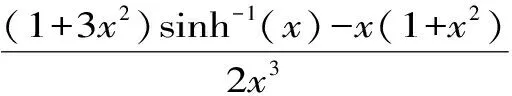关于Neuman-Sándor平均的三个最佳不等式
马 萍 , 杨月英
(湖州职业技术学院 机电与汽车工程学院, 浙江 湖州 313000)
关于Neuman-Sándor平均的三个最佳不等式
马 萍 , 杨月英
(湖州职业技术学院 机电与汽车工程学院, 浙江 湖州 313000)
给出了Neuman-Sándor平均关于第二类反调和平均与算术平均的最佳不等式,所得结论加强了已知结果。
第二类反调和平均; 算术平均; Neuman-Sándor 平均
一、引 言
对于p∈,a,b>0且a≠b,Neuman-Sándor平均M(a,b)[1]253-266 [2]49-59和p阶Lehmer平均Lp(a,b)[3]183-200定义为

(1)
Lp(a,b)=(ap+1+bp+1)/(ap+bp)
(2)
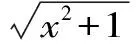
一般地,p阶Lehmer平均Lp(a,b)对于p∈和固定的a,b>0且a≠b是连续且严格单调递增的。特别地,L-1(a,b)=H(a,b)=2ab/(a+b)是调和平均,L-1/2(a,b)=G(a,b)=是几何平均,L0(a,b)=A(a,b)=(a+b)/2是算术平均,L1(a,b)=C(a,b)=(a2+b2)/(a+b)是第一类反调和平均和L2(a,b)=D(a,b)=(a3+b3)/(a2+b2)是第二类反调和平均。设a,b>0且a≠b,则第一类Seiffert平均P(a,b)和第二类Seiffert平均T(a,b)分别定义为
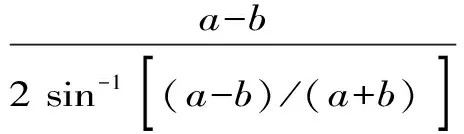
对于上述这些平均有以下不等式:
H(a,b) (3) 对所有a,b>0且a≠b成立。 近年来,Neuman-Sándor平均得到了深入的研究,数学工作者们从Neuman-Sándor平均M(a,b)发现了许多重要不等式[4] [5] [6] [7]567-577 [8] [9] [10] [11]。Neuman和Sándor[1]253-266 [2]49-59证明了不等式 对所有a,b>0且a≠b时成立。 在文献[12]637-643中Neuman证明了双向不等式 Cλ1(a,b)A1-λ1(a,b) λ2C(a,b)+(1-λ2)A(a,b) 对所有a,b>0且a≠b成立的充要条件是: 在文献[13]14-16 [14]299-302中作者发现了最佳参数α1,α2,β1,β2∈(0,1)使得双向不等式 α1D(a,b) +(1-α1)A(a,b) 对所有a,b>0且a≠b时成立。 杨月英等[15]207-217找到了最大值α1,α2和最小值β1,β2使得双向不等式 α1D(a,b) +(1-α1)G(a,b) 对所有a,b>0且a≠b时成立。 在文献[16]中,钱伟茂等证明了双向不等式 对所有a,b>0且a≠b成立的充要条件是: 从不等式(3)得到如下定理1.1、1.2和1.3。 定理1.1 双向不等式 α1D(a,b) +(1-α1)A(a,b) (4) 定理1.2 双向不等式 Dα2(a,b)A1-α2(a,b) (5) 定理1.3 双向不等式 (6) 为证明定理1.1-1.3,需要以下五个引理。 引理2.1 参见文献[17]中定理1.25,对于-∞ 在(a,b)内也单调递增(递减)。当f'(x)/g'(x)是严格单调时,那么上式也是严格单调的。 引理2.3 函数 (7) (8) 其中 (9) 从等式(9)得 (10) 对所有n≥0成立。注意到 (11) 所以,容易从引理2.2和(8)~(11)式得到引理2.3。 引理2.4 函数 (12) 证明:设φ1(t)=ln[sinh(t)/t],φ2(t)=ln[1+3sinh2(t)]-ln[1+sinh2(t)]。简单计算得到 (13) (14) 其中 (15) 由式(15)得 (16) 对所有n≥0成立。 (17) 所以,容易从引理2.1和等式(13)和(17)协同函数φ'1(x)/φ'2(x)的单调性得到引理2.4。 引理2.5 函数 (18) (19) 其中 (20) 由式(20)得 <0 (21) 对所有n≥0成立。注意到 (22) 所以,容易从引理2.2和(19)~(22)式得到引理2.5。 定理1.1的证明:因为D(a,b),A(a,b)和M(a,b)是对称和一阶齐次的,不失一般性,假设a>b>0。设x=(a-b)/(a+b),那么x∈(0,1)。则有 (23) 将(4)式变形为 (24) 利用等式(23),不等式(24)可变形为 (25) α1<Φ(t)<β1 (26) 其中,函数Φ(t)定义在引理2.3。 根据引理2.3协同不等式(24)-(26),可以得到不等式(4)成立的充要条件是: 定理1.2的证明:不失一般性,假设a>b>0。设x=(a-b)/(a+b),那么x∈(0,1)。将(5)式变形得 (27) 利用等式(23),不等式 (27)可变形为 (28) α2<φ(t)<β2 (29) 其中,函数φ(t)定义在引理2.4。 根据引理2.4协同不等式(27)-(29),可以得到不等式(5)成立的充要条件是: 定理1.3的证明:不失一般性,假设a>b>0。记x=(a-b)/(a+b),那么x∈(0,1)。将(6)式变形为 (30) 利用等式(23),不等式(30)可变形为 (31) α3<γ(t)<β3 (32) 其中,函数γ(t)定义在引理2.5。 根据引理2.5协同不等式(30)-(32),可以得到不等式(6)成立的充要条件是 : [3]LEHMERD H.On the Computing of Certain Means[J].J.Math.Anal.Appl.,1971(1). [4] QIAN W M,CHU Y M.On Certain Inequalities forNeuman-SándorMean[J].Abstr.Appl.Anal.,2013,Article ID 790783,6 pages. [5] ZHAO T H,CHU Y M,LIU B Y.Optimal Bounds forNeuman-SándorMean in Terms of the Convex Combinations of Harmonic,Geometric,Quadratic,and Contraharmonic Means[J].Abstr.Appl.Anal.,2012,Article ID302635,9pages. [6] SUN H,ZHAO T H,CHU Y M,LIU B Y.A Note on theNeuman-SándorMean[J].J.Math.Inequal.,2014(2). [7] LI Y M,LONG B Y,CHU Y M.Sharp Bounds for theNeuman-SándorMean in Terms of Generalized Logarithmic Mean[J]. J.Math.Inequal.,2012(4). [8] CHU Y M,LONG B Y,GONG W M,etc.Sharp Bounds for Seiffert andNeuman-SándorMeans in Terms of Generalized logarithmic Means[J].J.Inequal.Appl.,2013,10 pages. [9] CHU Y M,LONG B Y.Bounds of theNeuman-SándorMean Using Power and Identric Means[J].Abstr.Appl.Anal.,2013,Arti cle ID 832591,6 pages. [10] ZHAO T H,CHU Y M,JIANG Y L,etc.Best Possible Bounds forNeuman-SándorMean by the Identric,Quadratic and Contra-Harmonic Means[J].Abstr.Appl.Anal.,2013,Article ID 348326,12 pages. [11] HE Z Y,QIAN W M,JIANG Y L,SONG Y Q,etc.Bounds for the Combinations ofNeuman-Sándor,Arithmetic and Second Seiffer Means in Terms of Contra-Harmonic Mean[J].Abstr.Appl.Anal.,2013,Article ID 903982,5 pages. [12] NEUMAN E.A Note on a Certain Bivariate Mean[J].J.Math.Inequal.,2012(4). [13] 孟祥菊,刘 红,高红亚.第二类Seiffert平均的最优凸组合界[J].宁夏大学学报(自然科学版),2012(1). [14] 孟祥菊,王淑燕,田淑环.关于第二类Seiffert平均的最佳双边不等式[J].数学的实践与认识,2015(18). [15] YANG Y Y,SHEN L C,QIAN W M.The Optimal Convex Combination Bounds of Second Contra-harmonic and Geometric Mean for the Seiffert Means[J].Pac.J.Appl.Math.,2016(3). [16] QIAN W M,SONG Y Q,ZHANG X H,etc.Sharp Bounds for Toader Mean in Terms of Arithmetic and Second Contra-harmonic Means[J].J.Func.Spaces,2015,Article ID 452823,5 pages. [17] ANDERSON D.D.,VAMANAMURTHY M.K,VUORINEN M.K.Conformal Invariants,Inequalities,and Quasiconformal Maps, Canadian Mathematical Society Series of Monographs and Advanced Texts[M].New York,NY,USA:John Wiley & Sons,1997. ID 932061,11 pages. ThreeOptimalInequalitiesforNeuman-SándorMean MA Ping , YANG Yue-ying (School of Mechanic Electronic & Automotive Engineering, Huzhou Vocational and Technological College, Huzhou 313000, China ) In the article, we present optimal inequalities for the Neuman-Sándor means in terms of the sencond contra-harmonic and arithmetic means. The given results are the improvements of some known result. second contra-harmonic mean; arithmetic mean; Neuman-Sándor mean 2017-01-09 本文系2016年度湖州职业技术学院教改课题“基于自动化类专业课的《应用数学基础》课程教学研究”(2016xj26)的成果。 马 萍(1963-),女,浙江临海人,副教授,主要从事解析不等式研究;杨月英(1979-),女,湖南益阳人,副教授,计算数学硕士,主要从事解析不等式研究。 0151.25 A 1672-2388(2017)03-0069-05



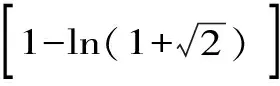
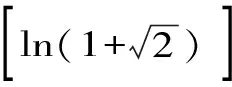
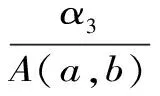
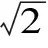
二、引 理
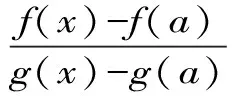
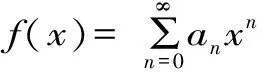

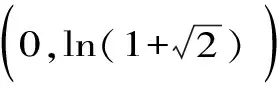

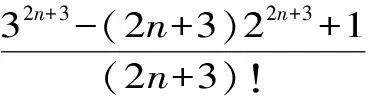
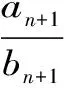

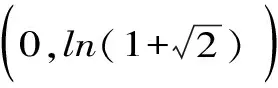
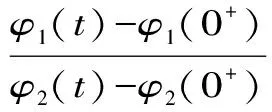
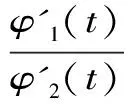
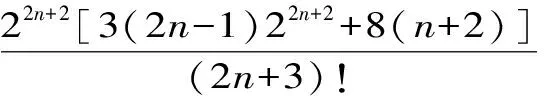


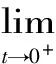

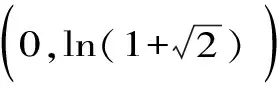

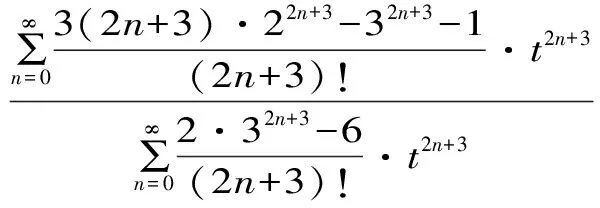
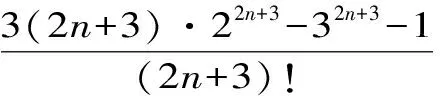

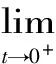
三、定理的证明