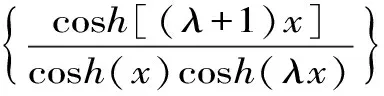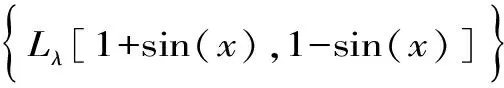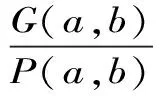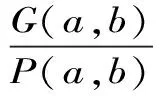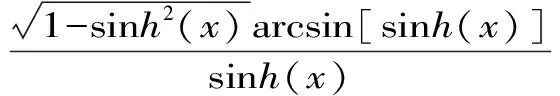Sándor平均的Lehmer平均界及其应用
钱 伟 茂
(湖州职业技术学院 远程教育学院, 浙江 湖州 313000)
Sándor平均的Lehmer平均界及其应用
钱 伟 茂
(湖州职业技术学院 远程教育学院, 浙江 湖州 313000)
通过研究发现了最大值λ和最小值μ,使得双向不等式Lλ(a,b)
Sándor平均;p阶Lehmer平均;双向不等式
一、前 言
设p∈和a,b>0且a≠b,则p阶Lehmer平均Lp(a,b)[1]183-200定义为:
(1)
众所周知,p阶Lehmer平均Lp(a,b) 对于固定的a,b>0且a≠b,关于p∈是严格单调递增的。许多对称二元平均是p阶Lehmer平均的特殊情形。例如:L-1(a,b) =2ab/(a+b)=H(a,b) 是调和平均,L-1/2(a,b)==G(a,b)是几何平均,L0(a,b)=(a+b)/2=A(a,b)是算术平均等。
设a,b>0且a≠b,P(a,b) =(a-b)/[2arcsin((a-b)/(a+b))]是第一类Seiffert平均,则Sándor平均X(a,b)[2]409-413定义为:
X(a,b)=A(a,b)eG(a,b)/P(a,b) -1
(2)
2014年,Sándor[3]1-9得到了以下不等式:

对所有a,b>0且a≠b成立,其中L(a,b)=(a-b)/(lna-lnb)是对数平均。
杨镇杭和周爽爽等[4] [5]证明了双向不等式:
M1/3 钱伟茂等[6]证明了双向不等式: α1A(a,b)+(1-α1)H(a,b) α2A(a,b)+(1-α2)G(a,b) H[α3a+(1-α3b)+(1-α3a)] G[α4a+(1-α4b)+(1-α4a)] 本文的主要目的是寻找并证明最大值λ以及最小值μ,使得双向不等式: Lλ(a,b) 对所有a,b>0且a≠b成立。 定理1 双向不等式: Lλ(a,b) 对所有a,b>0且a≠b成立当且仅当λ≤-1/3且μ≥0。 证明:根据Lp(a,b)和X(a,b) 是对称且一阶齐次的,不失一般性,假设a=x>1且b=1。设p∈,则从(1)式和(2)式可得: (3) 设 (4) 简单计算得: F(1+)=0 (5) (6) 其中: (7) (8) 其中: f(x)=3x4p+3+x4p+2-p(2p-1)x3p+4+(2p2+9p+7)x3p+3+(2p2-5p+2)x3p+2 -(2p2+5p+1)x3p+1+px2p+4+(14p+5)x2p+3-(14p+5)x2p+1-px2p +(2p2+5p+1)xp+3-(2p2-5p+2)xp+2-(2p2+9p+7)xp+1+p(2p-1)xp-x2-3x (9) 现分四种情形进行证明。 情形1:当p=-1/3时,则(9)式变成: (10) 等式(6)-(8)和(10)导致的结果是函数F(x)在区间(1,∞)严格单调递增。 所以,可从(3)-(5)式和函数F(x)的单调性得到: X(a,b)>L-1/3(a,b)。 情形2:当p>-1/3时,设x>0和x→0,从(1)式和(2)式协同Taylor展式给出: (11) 等式(11)意味着存在充分小的δ1=δ1(p)使得 X(1,1+x) 对所有x∈(0,δ1)成立。 情形3:当p=0时,则从(9)式得到: f(x)=16x(x2-1)>0 (12) 对所有x>1成立。 所以,容易从(3)-(8)和(12)式得到: X(a,b) 情形4:当p<0时,从(1)式和(2)式可得: (13) 等式(13)意味着存在充分大的X1=X1(p)>1使得 X(x,1)>Lp(x,1) 对所有x∈(X1,+∞)成立。 应用定理1可得四个涉及双曲函数、三角函数和反双曲函数的精确不等式。 设a>b>0和x=arctanh[(a-b)/(a+b)]=(lna-lnb)/2∈(0,+∞)。经过简单计算可得: (14) 根据(14)式和定理1可得定理2。 定理2 双向不等式 对所有x∈(0,+∞)成立,当且仅当λ≤-1/3且μ≥0。 设a>b>0和x=arcsin[(a-b)/(a+b)]∈(0,π/2)。容易得到: (15) 从(15)式和定理1可得定理3。 定理3 双向不等式 对所有x∈(0,π/2)成立,当且仅当λ≤-1/3且μ≥0。 设a>b>0和x=arctan[(a-b)/(a+b)]∈(0,π/4)。经过简单计算得到: (16) (17) 从(16)和(17)式协同定理1可得定理4。 定理4 双向不等式 对所有x∈(0,π/4)成立当且仅当λ≤-1/3且μ≥0。 (18) (19) 根据(18)式和(19)式协同定理1得到定理5。 定理5 双向不等式 [1] LEHMER D H.On the Compounding of Certain Means[J].J.Math.Anal.Appl.,1971(4). [4] YANG Z H,WU L M,CHU Y M.Sharp Power Mean Bounds for Sándor Mean[J].Abstr.Appl.Anal.2014,Article ID 172867,2014. [5] ZHOU S S,QIAN W M,CHU Y M,etc.Sharp Power-type Heronian Mean Bounds for the Sándorand Yang Mean[J].J.Ianequal. Appl.,2015:159,2015. [6] QIAN W M,CHU Y M,ZHANG X H.Sharp Bounds for Sándor Mean in Terms of Arithmetic,Geometric and Harmonic Means[J]. J.Ianequal.Appl.,2015:221,2015. SharpLehmerMeanBoundsforSándorMeanwithApplications QIAN Wei-mao (School of Distance Education, Huzhou Vocational and Technological College, Huzhou 313000, China ) In the article, the authors find the greatest values λ and the least values μ such that the double inequalitiesLλ(a,b) Sándor mean;p-th Lehmer mean; double inequalities 2016-12-12 本文系2013年度浙江省自然科学基金项目“拟双曲度量和拟共形映射的稳定性理论研究”(LY13A010004),2015年度浙江广播电视大学科研课题“Schwab-Borchardt平均及其不等式”(XKT-15G17)的研究成果之一。 钱伟茂(1962-),男,浙江海宁人,教授,主要从事拟共形映射、特殊函数和平均值理论研究。 O174.6 A 1672-2388(2017)03-0065-04


二、主要结果
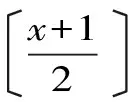
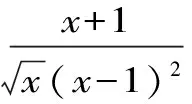
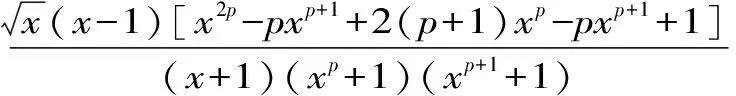
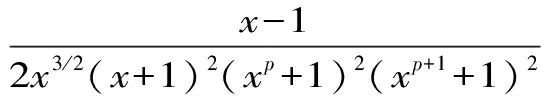
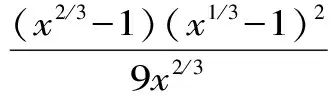
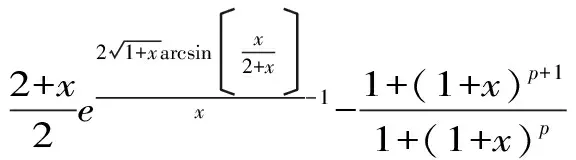
三、应 用