引导学生自主操作的新探究
滕敏健
(浙江省桐乡市实验小学教育集团春晖小学)
引导学生自主操作的新探究
滕敏健
(浙江省桐乡市实验小学教育集团春晖小学)
新课程强调学生自主学习,体现在学生学具操作探究的过程中,要给予学生更多自主的机会,充分发挥他们借助操作理解数学的主动性和积极性。然而调研发现,学生数学课堂在操作上存在没有把握好时机,走过场,没有深入地分析总结,没有发挥价值所在等问题。
学生操作 问题 自主操作 策略
目前学生数学课堂在操作上主要存在以下问题:(1)学生被动操作,学生操作受教师或者同学支配的现象较突出,较少有选择权。(2)学生操作的机会不均等,尤其在合作操作过程中,往往只有少数几个优秀生在操作,而较多学生只是旁观者。(3)操作走过场,为操作而操作,目的性不强。存在这些问题的数学课堂,学生的操作是被动的,效率是低下的,有时只是形式而已,达不到操作想要达到的真正目的。为此,教师要结合课堂教学的实际需要,让学生自主操作,在活动中“感悟”“经历”“体验”数学知识的形成过程。在动手实践过程中发现问题、思考问题,在合作讨论中解决问题。自主指自己做主,不受别人支配,操作是指人用手活动的一种行为。可见,自主操作的主体是学生,是一种手脑并用的有效行为,而不是随意的一种摆设。
苏霍姆林斯基也曾说:“在儿童的心灵深处,有一种根深蒂固的需要,那就是希望自己是一个发现者、研究者、探究者。”只有通过自主操作发现问题、解决问题,课堂上营造一种温馨的思维空间和气氛,才能充分发挥学生操作的热情和潜能,真正收到好的教学效果。
引导学生自主操作的策略
(一)积极体验,初步感知
皮亚杰曾说:“数学的抽象仍是属于操作性质的,它的发生发展要经过连续不断的阶段。而其最初的来源又是十分具体的行动。”小学生的年龄特点和认知规律,决定他们数学学习离不开操作感知这一基本途径。
1.折折拼拼,体会特征
教师积极创造条件,组织学生动手操作,以此来帮助学生参与知识的形成过程,使他们在亲身体验和探索中认识和感悟图形的特征,理解和掌握图形拼组的规律所在,发展学生的思维,提高实践能力。
例如,人教版一年级下册《平面图形的转换和拼组》教学,如果向学生灌输知识,学生对长方形对边相等、正方形四条边相等的特征,图形拼组中的很多细节感知都会是干巴巴的,所学的知识是有“形”无“神”的。通过让学生折一折体会长方形对边相等,通过折让小朋友直观感知图形之间的转化:有的把长方形纸折成了(如图1)两个长方形;有的折成(如图2)两个长方形,效果就完全不同了。

图1
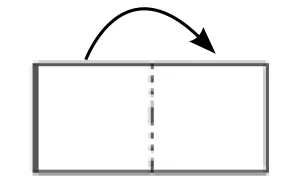
图2
2.搭搭想想,直观体验
通过操作活动,引导学生在观察、对比、反思中抽象数学。教师要重视学生“动态操作”后的“静态的数学思考”。
例如,在教学“有余数的除法”时,让学生用小棒操作后填表格(如图3)。反馈时,学生根据自己的亲身体验发现,有些正好分完,没有剩余;有些没有分完,还有剩余,初步体验“余数”所蕴含的意义。
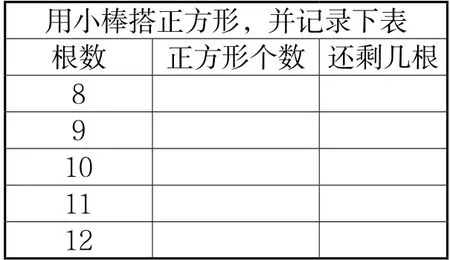
图3
(二)积累经验,逐步抽象
数学教学应该向学生提供从事数学活动与交流的机会,帮助他们在自主探索的过程中,真正理解和掌握基本的数学知识与技能、数学思想与方法。所以在教学过程中,我们要把数学看成一种充满情感、富于思考的经历体验和探索的活动。
1.找出联系,理解算理
借助学具的操作,并且善于找出实物与算式之间的内在联系,能较好地帮助学生理解算理。例如,教学进位加法“6+5=?”时,(如图4)让学生摆一摆,圈一圈,说一说,然后尝试让他们根据自己的操作过程用分解式写出来。经过多次操作、交流,学生能逐步理解进位加法的“凑十法”的算理。
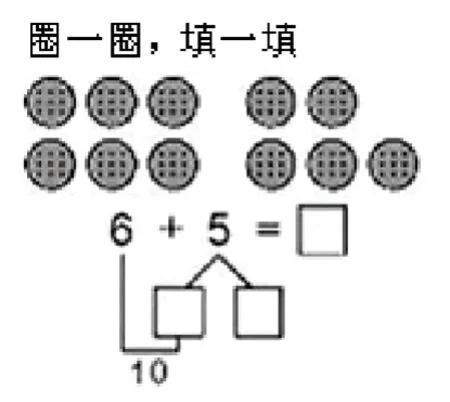
图4
2.合理分工,合作操作
合作是指两个或两个以上的学生或群体,为了达到共同的目的而在行动上相互配合的过程。合作操作是合作学习的重要组成部分,教师以学生学习小组为重要的推动性,通过指导小组成员展开合作,发挥群体的积极功能,提高个体的学习动力和能力,达到完成特定的教学任务的目的,从而激发学生的主动性、创造性,也因此得以充分地发挥。为了达到人人有责任,个个在探索的目的,有必要进行合理分工。
例如,在教学《两位数除以一位数》“52÷2=?”时,让学生在合作小组里拿出小棒来分一分、说一说。组长进行分工后,有的先拿出4捆小棒,每份2捆;有的把剩下的一捆和零散的2根合起来,共12根,平均分成两份,每份可以分到6根;有的进行记录等,结果发现每份共可以分得26根(如图5)。教师根据学生说的过程慢慢写竖式,让他们感知这个操作过程跟竖式之间的关系,慢慢理解除法竖式的含义。
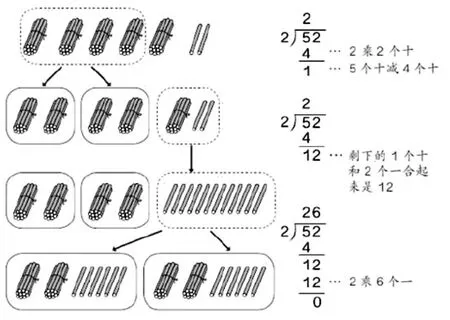
图5
(三)逐渐深化,理性提升
心理学研究表明,小学生的思维是从具体形象思维到抽象逻辑思维过渡的,小学生的思维特点决定了教学中应尽可能地联系学生已有的经验,创设问题情境,在直观操作中体验知识的发生、发展过程,在交流反馈中,对知识技能进行梳理建构,对思想方法进行理性提升。
1.思维冲突,加深理解
碰到一些具有思维冲突的情境,经过学生自己实践操作、探究体验,不仅能感受理解知识的产生与发展过程,也能感悟到观察、操作、比较、归纳、推理、概括、转化等数学思想方法。
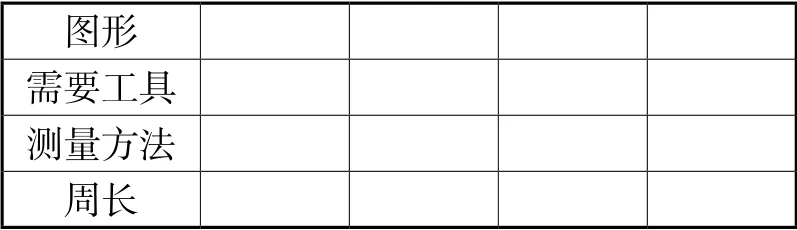
图6
例如,在《认识周长》一课,我给学生发里面装有一张长方形、正方形、三角形、树叶、硬币、线等的工具包以及记录表(图6),让学生小组合作动手测量它们的周长。像长方形、正方形等直边的图形用直尺容易得出图形的周长,而像树叶这样不规则的物体,无法用直尺进行测量,能引起孩子们的思维冲突。于是,经过思考,终于有人想出用线围着树叶的边缘一周,再把细线拉直,用直尺量线的长度。这个过程让他们深刻理解周长的本质含义,也初步体现了“化曲为直”的思想方法。
2.解决问题,发现规律
数学问题是千变万化的,学生面对一些疑难问题,如果不借助操作,有时是很难解决的,而通过直观地摆一摆等方法,孩子们就能在老师的引导下或者自己的感悟中解决问题。例如,用12个小正方形学具摆长方形,有几种不同的摆法,它们的周长相等吗?你能发现什么规律?孩子们无从下手。有学生问:“老师能不能用正方形摆一摆?”这给大家启发,他们自觉分成学习小组进行操作,结果发现了图7所示的3种不同结果。图形摆得越紧密,重合的边越多,这样它的周长就越短,相反,它的周长就越长。这样的规律,如果没有孩子们的亲身经历,是很难理解其中道理的。
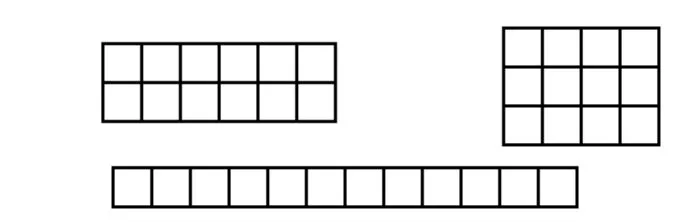
图7
综上所述,数学知识的学习过程,就是学生对数学知识的探究过程。只有给予学生自主的探究时间和空间,以学生自己喜欢的方式自由探索、发现、交流,让不同层次的学生真正经历一个自主探索的过程,才能让学生感悟知识的本质、构建数学模型,走向思维深处。
[1] 钱科英.让思维在操作之后的理性思辨中走向深入[J].小学数学教师,2016(1).
[2] 张卫星.例谈小学数学模型的建构方式[J].小学月刊小学数学版,2015(7-8).
[3] 李秀银.感性体验,理性提升[J].中小学数学,2015(9).
[4] 王家元.让学生在经历学习的过程中,积累数学基本活动经验[J].新课程:教师版, 2013(3).
责任编辑:王天舒

