多级轴流压气机静子三维造型优化设计
米 攀,李清华,安利平
(中国航发四川燃气涡轮研究院,成都610500)
多级轴流压气机静子三维造型优化设计
米 攀,李清华,安利平
(中国航发四川燃气涡轮研究院,成都610500)
以Isight为优化平台,通过集成三维造型程序、CFD计算程序与多岛遗传算法,搭建了一套三维造型优化设计系统。以高效高负荷多级轴流压气机的前两级为研究对象,针对第一级静子根区存在的角区分离,对其50%叶高以下的3个主要叶片造型控制参数的径向分布形式进行了优化。结果表明:优化叶型有效削弱了第一级静子的角区分离,根部区域的总压恢复系数最大增加了1.8%,且改善了级间匹配,提高了压气机效率。
航空发动机;轴流压气机;三维造型;数值优化;遗传算法;级匹配
1 引言
随着航空发动机对推重比要求的提高,压气机级负荷不断增加,其设计难度也越来越大。由于叶片造型和级间匹配的设计参数较多,造成单叶排径向匹配和级间匹配成为压气机设计的主要难点之一。其设计需花费大量的时间和精力,且对设计经验的依赖性较强。但在实际设计中发现,通过将优化算法与正问题数值计算分析相结合,可为高性能压气机的设计提供有效参考,提高设计效率,减少对设计经验的依赖。为此,国内外研究人员开展了大量研究工作。Astrua等[1]借助数值模拟,采用人工神经网络与随机漫步法对跨声轴流压气机转子叶型进行了三维优化,在设计点流量不变情况下,设计点与非设计点性能均得到改善。Okui等[2]在对一台跨声压气机单转子叶型积叠轴进行的多目标优化中,前掠使峰值效率增加了0.3%,后掠与S型中弧线结合使效率提高0.6%。在级优化中,级效率提高0.7%。国内研究人员[3-4]的优化结果也表明,借助三维造型优化设计,风扇/压气机转子性能有较大提升。
纵观上述文献,多以单一截面或单叶排环境的优化居多,忽略了多级间的性能匹配对优化目标的影响。本文以某高负荷多级高压压气机的前两级为研究对象,对第一级静子多个设计参数的径向分布形式进行优化,通过减小静子角区分离,改善多级压气机的性能匹配,以提高压气机效率。
2 数值模型与优化方法
2.1 数值计算模型
该压气机具有高级负荷、高效率的技术指标。通过多轮设计修改,总体性能基本达到了技术指标;但第一级静子根部存在一定分离,且多次修改流道和叶片造型参数后仍无法消除。为此,本次优化主要针对其第一级静子角区进行。为控制计算量,仅以多级压气机的前两级为对象,在多级匹配情况下研究单叶排优化对性能的改善。
数值计算网格由北京航空航天大学宁方飞发展的Turbomesh2.0网格程序生成[5],所有叶排采用单通道,对每个叶片通道,叶片周围采用O型网格,叶片上游、下游和叶片通道内采用H型网格。图1给出了数值计算的网格模型。为尽量接近压气机真实几何结构,网格模型考虑了压气机转子尖部间隙、可调静子部分间隙以及根部倒圆。表1给出了网格模型拓扑结构,其中静子间隙为轴向部分间隙,转子间隙为轴向全间隙。

图1 数值计算网格模型示意图Fig.1 Numerical calculation grid model

表1 数值计算网格拓扑模型Table 1 Topological model of numerical calculation
数值计算求解三维雷诺平均N-S方程,湍流模型选择Spalart-Allmaras一方程模型。计算进口边界给定总温、总压与气流角,出口边界给定静压。调节出口静压来逼近数值边界点,数值发散前的最后一个工况对应数值近失速点。具体的计算方法、格式和模型介绍参见文献[5-6]。
2.2 三维造型优化方法
以Isight为优化平台开展三维造型优化,图2为优化系统的流程示意图。寻优方法采用多岛遗传算法,优化前期需指定优化变量与优化目标,通过试验设计确定初始种群中各个体变量值。对初始种群个体进行三维造型与数值计算,根据计算结果提取优化变量与优化目标的适应关系。在初始种群中选出较优个体进行交叉与变异,得到后代种群个体。对后代个体再次进行三维造型与数值计算,判断是否满足优化目标。若不满足则重新计算个体适应度并生成下一代种群,直到满足优化目标,最终输出最优造型方案。整个优化过程集成了叶片造型程序、CFD程序以及多岛遗传算法,形成了一套三维造型优化设计系统。

图2 优化流程示意图Fig.2 Optimization flowchart
在造型程序中,以三次样条函数对叶片造型主要控制参数的径向分布形式采用径向7点进行参数化。在不影响叶片结构强度性能前提下,选取叶片造型的主要影响参数作为优化参数。本次优化目的是控制第一级静子根部分离,所以仅选取落后角、最大相对厚度位置与最大挠度位置在其50%叶高以下的3个控制点作为优化变量。图3给出了各变量参数化分布形式以及扰动的上下限。各变量在指定的范围内进行扰动,采用可控扩散叶型造型方法构造三维叶片。优化过程中通过改变落后角与最大挠度位置对叶型中弧线进行修正,最大相对厚度位置可对厚度分布进行修正,叠加修正后的中弧线与厚度分布可得到不同叶高基元叶型的吸/压力面型线,最后通过径向积叠得到三维叶片。
优化过程中,以压气机设计点作为优化工况点,所有数值计算的网格模型与计算模型一致,并保证出口背压不变。以优化压气机效率为目标,通过反复恰当的使用遗传算法的择优原则对静子造型控制参数的分布形式进行修正,改善压气机内部流动,提高压气机效率,直到压气机效率在优化过程中基本收敛,最终得到最优静子叶型。

图3 各优化变量分布形式及其扰动范围Fig.3 Optimal variables and their perturbation bounds
3 优化结果与分析
图4给出了压气机效率优化收敛过程。因计算周期较长,优化过程中对迭代步数进行了限制。在优化后期,压气机效率提高已基本接近收敛。针对最终叶型进行性能分析,图5为优化前后压气机的性能对比。由图可知,优化后压气机近堵点流量减小0.04%,近失速点流量减小0.17%。优化前后压气机压比基本不变,但效率有一定增加,其中优化点D′相对于原始点D增加了0.6%。

图4 压气机效率收敛过程Fig.4 The convergence history of compressor efficiency

图5 优化前后压气机性能对比Fig.5 Comparison of compressor performance before and after optimization
图6给出了第一级静子在叶片优化前后的实体对比和部分截面叶型对比。由于优化变量的控制点位于径向50%叶高以下,所以优化前后100%与50%叶高的叶型完全重合。静子根部区域的截面叶型以及实体有一定改变。10%叶高截面叶型对比表明,最大挠度位置后移,叶型安装角增加。图7给出了优化前后的静子安装角对比,在相同压比点,安装角增加可能引起压气机流量减小。
图8为优化前后一级静子吸力面与10%叶高的马赫数分布云图。吸力面马赫数分布云图表明,优化后静子根部分离区明显减小。对比10%叶高截面马赫数分布云图,在叶型前半段,气流经历了先加速后减速的过程。原始叶型中,由于最大绕度位置靠前,气流在前半段弦长范围内过早减速导致气流轴向速度与通道逆压梯度不匹配,气流在中间弦长开始形成分离,分离由叶根向叶尖发展,进而引起整个根部角区分离。优化后由于叶型最大挠度位置后移,气流在叶型前段弦长范围内加速段延长,最大马赫数位置M′相对于M后移,气流在叶型中后段弦长范围内的速度相对于原始叶型的增加,加速气流能有效抵抗通道内的逆压梯度,减小根区分离。
图9为优化前后静子10%叶高的壁面静压分布对比。可见,在原始叶型吸力面,气流在前段迅速降压增速,并在15%轴向弦长达到最小静压,对应图8中M点。15%轴向弦长到50%轴向弦长,气流增压降速;中间弦长以后,由于气流分离,叶型静压升能力降低。在原始叶型压力面,叶型静压升集中在40%轴向弦长之前,在40%轴向弦长之后静压有一定减小。优化后的叶型吸力面前段加速区更长,气流在25%轴向弦长处的静压值达到最小,且最小静压值比原始叶型的低,说明图8中M′点的马赫数比M点的大。由于分离明显减弱,在25%轴向弦长到叶型尾缘,吸力面气流静压持续增加。在压力面,气流静压升分布更加均匀。优化后叶型前缘的吸/压力面静压曲线交叉点后移,叶型进口负攻角增加,有利于增加压气机裕度。

图6 优化前后静子实体与各截面叶型对比Fig.6 Comparison of blade solid and section before and after optimization

图7 优化前后安装角对比Fig.7 Comparison of the stagger angle before and after optimization

图8 静子马赫数云图Fig.8 Stator relative Mach number

图9 静子10%叶高静压分布Fig.9 The distribution of static pressure at 10%span
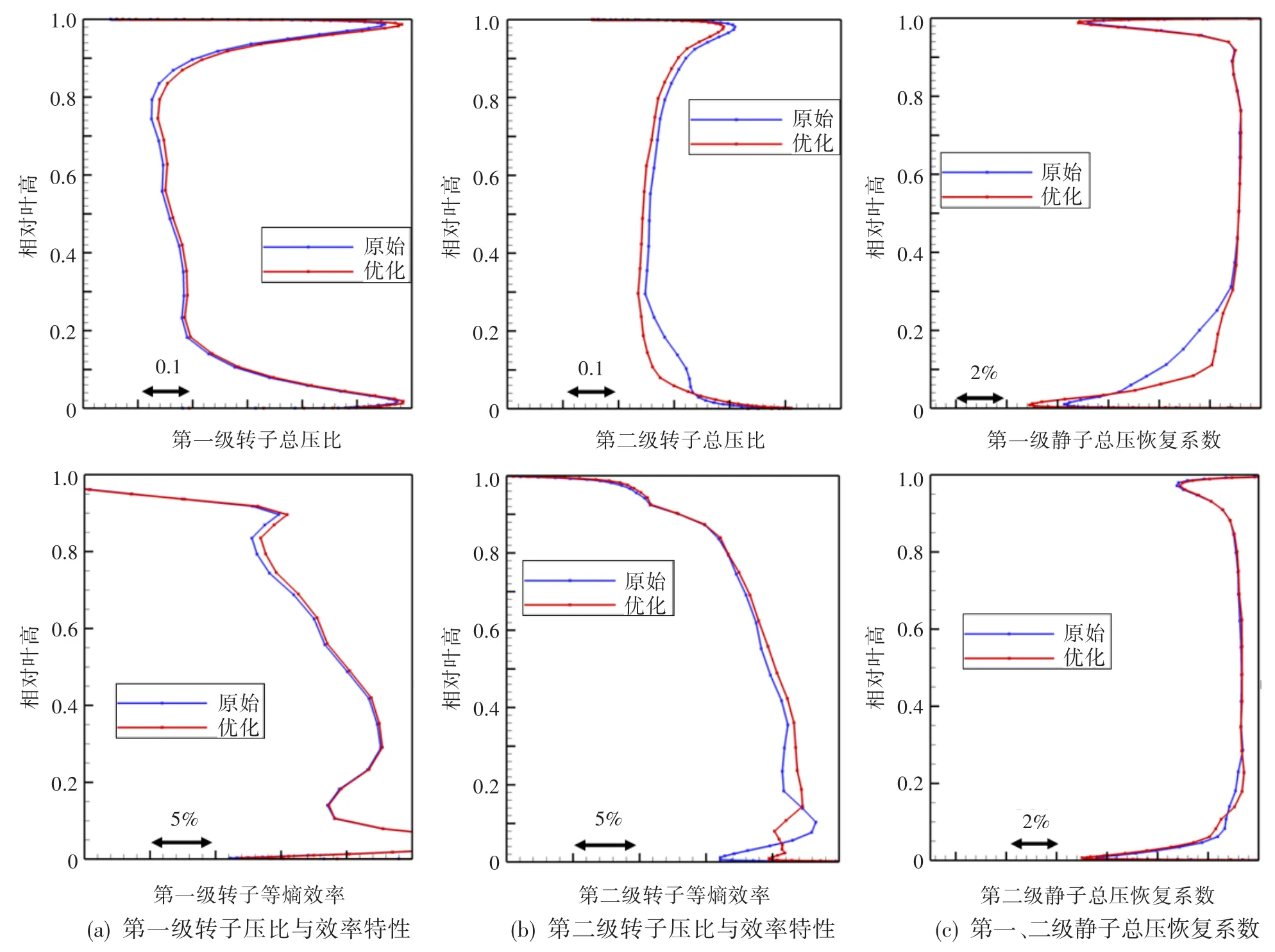
图10 优化前后各排叶片特性参数径向分布Fig.10 The radial distribution of blade characteristics before and after optimization
对第一级静子10%叶高马赫数与壁面静压的分析结果表明,在原始叶片中,由于根区叶型最大绕度靠前,吸力面气流过早完成降压加速过程,导致叶片中后段气流速度不能克服通道逆压梯度,进而引起分离。优化叶片通过调整弯度分配,使气流在叶片前段充分加速,有效控制了端区分离。
为分析各级匹配改善情况,图10给出了特性线上D点优化前后压气机各级径向特性参数对比。优化后第一级静子安装角增加引起压气机进口流量减小,第一级转子压比与效率在60%到90%叶高范围内有一定增加。第一级静子在有效减小角区分离后,根部区域的总压恢复系数最大增加了1.8%。在压气机总压比不变情况下,由于前面级性能的改善,第二级转子负荷相对减小,其中根部区域的压比减小较多,并在10%到60%叶高范围内效率有一定增加;第二级静子根部区域总压恢复系数也有一定改善。整体上,在对第一级静子优化中,通过调整静子总压恢复系数与安装角,改善了多级环境中各叶排间的性能匹配,压气机总体性能改善。
4 结论
针对某高效高负荷多级压气机第一级静子端区存在的角区分离,利用搭建的三维优化系统,对静子的造型参数进行了三维优化。优化结果表明:降低静子前段弯度分配,能有效控制根区分离,提高静子总压恢复系数,并改善多级压气机前后叶排的性能匹配,压气机效率最大增加了0.6%;该优化设计技术可有效改善压气机性能。
[1]Astrua P,Piola S,Silingardi A,et al.Multi-objective con⁃strained aero-mechanical optimization of an axial com⁃pressor transonic blade[R].ASME GT2012-68993,2012.
[2]Okui H,Verstraete T,Alsalihi Z,et al.Three dimensional design and optimization of a transonic rotor in axial flow compressors[R].ASME GT2011-45425,2011.
[3]Zheng R Y,Xiang J H,Sun J J.Blade geometry optimiza⁃tion for axial flow compressor[R].ASME GT2010-22229,2010.
[4]黄 磊,余华蔚.单级跨声速风扇转子叶片多目标优化设计[J].燃气涡轮试验与研究,2016,29(3):30—34.
[5]宁方飞.考虑真实几何复杂性的跨音压气机内部流动的数值模拟[D].北京:北京航空航天大学,2002.
[6]Ning F F,Xu L P.Numerical investigation of transonic compressor rotor flow using an implicit 3D flow solver with one-equation Spalart-Allmaras turbulence model[R].ASME 2001-GT-0359,2001.
3D optimization design of multi-stage axial flow compressor stator
MI Pan,LI Qing-hua,AN Li-ping
(AECC Sichuan Gas Turbine Establishment,Chengdu 610500,China)
With Isight as an optimization platform,a 3D optimization design system of compressor blade was composed by 3D blade design procedure,CFD procedure and multi-island genetic algorithm.For the first stage stator hub with corner separation,the first two stages of a high load multi-stage axial flow com⁃pressor were studied.The radial distribution of 3 main blading control parameters under the middle span was optimized.The optimization results show that the stator's total pressure recovery coefficient increased by 1.8%as the corner separation was effectively weakened,and the improvement of the matching between stages increased the compressor efficiency.
aero-engine;axial flow compressor;3D profile;numerical optimization;genetic algorithm;stage matching
V231.3
A
1672-2620(2017)05-0013-05
2016-12-16;
2017-03-01
米 攀(1985-),男,四川广安人,工程师,主要从事压气机气动设计研究。

