基于截尾概率－非概率混合模型的可靠性优化算法

周凌，李艳辉

基于截尾概率－非概率混合模型的可靠性优化算法

周凌＊，李艳辉

中国科学院长春光学精密机械与物理研究所，长春 130033

针对工程中截尾概率变量与非概率变量同时存在的情况，给出一种新的截尾概率与非概率混合可靠性模型。在该混合可靠性模型基础上，按照可靠性指标（RIA）法给出双层嵌套可靠性优化模型，并采用改进搜索策略后的ST－Powell优化算法在外层搜索设计变量的最优值，内层采用能保证收敛的改进的有限步长迭代法求解混合可靠性指标。数值算例表明，改进搜索策略后的ST－Powell优化算法的全局寻优性得到显著提升；改进搜索策略后的ST－Powell优化算法与改进的有限步长迭代法相结合求解双层嵌套混合可靠性优化模型的正确性得到验证，且对于非线性程度较高的极限状态函数同样能够得到满足截尾概率与非概率混合可靠性模型指标要求的最优解，并对工程结构算例具有很好的适应性。

截尾概率变量；非概率变量；混合可靠性模型；改进搜索策略后的ST－Powell优化算法；改进的有限步长迭代法；可靠性优化

自然界中不确定信息是广泛存在的，因而在工程中对关键重要结构只进行确定性优化设计是不够的，有必要进行可靠性基础上的优化设计［1－3］。除了传统概率可靠性分析及其基础上的优化设计，目前越来越多的文献考虑传统概率与非概率变量混合存在情况下的结构混合可靠性分析及优化设计［4－7］。这是因为在工程实践中经常遇见某些变量的数据样本较少，而其他变量的数据样本充足的情况。对于数据样本充足的变量，能够得到不确定变量的准确概率分布，采用传统概率变量进行描述是合适的；对于数据样本较少的不确定变量，准确的概率分布无法得到，而变量分布的微小误差会导致最终可靠性计算结果有较大误差，此时采用传统概率变量进行描述是不合适的，而其边界容易获得，按照Ben－Haim思想采用非概率变量进行描述较为合适［8－9］。因而对于概率与非概率混合可靠性及其优化的研究已成为一个热点研究领域。

Luo等［4］提出一种新的随机变量与多维超椭球凸集合非概率变量的混合可靠性模型，并采用高效的迭代算法求解混合可靠性指标。Jiang等［10］对随机变量与区间变量同时存在的结构断裂问题进行了研究，结构断裂可靠性指标区间由基于响应面法的高效迭代算法得到。Qiu和Wang［5］基于概率可靠性模型与区间数学方法，给出了结构系统的概率可靠性指标的区间。Yang等［11］采用 Monte－Carlo法与Kriging模型对概率变量与凸集合变量同时存在的混合可靠性模型进行了求解。Wu等［12］提出采用统一的区间随机抽样方法求解带有随机与区间不确定系统参数的工程结构的断裂破坏载荷上下界的统计特性。王军和邱志平［13］先将功能函数进行非概率可靠性分析，然后将标准化区间变量空间所有区域的可靠度进行求和计算，给出一种新的概率－非概率混合可靠性模型。孙文彩等［14］提出根据区间变量是否相关和问题的精度要求，在区间变量域中按照一定规则抽取一定量的实现值，将对应的随机失效度的平均值作为结构失效度的近似值，从而形成随机－区间混合变量下的结构可靠性分析模型。

Du等［6］给出了混合可靠性模型的优化设计与求解算法。程远胜等［7］研究了概率和区间不确定性条件下的结构鲁棒设计方法。Ge等［15］对带有随机变量与区间变量的复合材料结构进行了基于混合可靠性模型的优化设计。基于文献［4］提出的混合可靠性模型，罗阳军等［16－17］对带有概率与非概率不确定信息的粘接钢筋混凝土复合材料梁、导弹翼面进行了混合可靠性基础上的优化设计。Xia等［18］采用混合扰动随机矩法估算目标函数，运用混合扰动逆映射法求解零件可靠性，这样将嵌套的随机与区间混合可靠性优化模型转换成单个循环求解过程，以此提高计算效率。

以上文献给出的混合可靠性模型中随机变量的分布区间是无穷大的，而在工程可靠性应用的大多数情况下，随机变量的分布是有界的，因而采用截尾随机变量代替随机变量更为合适［19］。文中将给出截尾随机变量与多维超椭球凸集合非概率变量同时存在的混合可靠性模型及其基础上的优化算法。首先给出混合可靠性模型指标定义与求解步骤；然后基于可靠性指标（RIA）法给出混合可靠性基础上的优化模型与求解方法，其中外环采用改进搜索策略的ST－Powell优化算法搜索设计变量最优值，内环采用改进的有限步长迭代法求解混合可靠性指标，并分别给出了内环改进的有限步长迭代法求解混合可靠性指标的步骤，以及改进搜索策略后的ST－Powell优化算法的计算步骤；最后，通过算例验证改进搜索策略后的ST－Powell优化算法搜索的全局性、改进搜索策略后的ST－Powell优化搜索算法与改进的有限步长迭代法相结合搜索混合可靠性基础上设计变量最优值的正确性，以及对非线性程度较高的极限状态函数的混合可靠性基础上优化搜索的适应性。

1 混合可靠性模型指标定义

在工程实践中，同一分析对象中的不确定变量根据数据样本是否充足而分别采用截尾随机变量（代替随机变量）与多维超椭球凸集合非概率变量进行描述［4，16］，其中区间变量是多维超椭球凸集合非概率变量的一种特殊形式，因而在对其进行可靠性评估时，会存在截尾随机变量与非概率变量存在于同一个极限状态函数中的情况。式（1）给出了带有截尾随机变量与多维超椭球凸集合非概率变量的极限状态函数。

式中：珚X为截尾随机向量；Y为多维超椭球凸集合向量；珡Xi为第i个截尾随机变量；Yj为第j个超椭球凸集合向量。

目前对于随机变量与非概率变量混合存在的可靠性指标的定义都是基于传统概率可靠性指标β的定义发展而来的，混合可靠性指标求解是一双层优化模型，即内层在非概率变量约束下搜索极限状态函数的最小值，外层在传统概率空间迭代求解概率可靠性指标β［4，11］。然而当前的混合可靠性模型不能适应截尾随机变量与非概率变量混合存在的情况，因为会存在β取值为无穷大的情况，若采用迭代算法则无法求解。下面以最简单极限状态函数中只包含强度珚R（截尾随机变量）与应力S（区间变量）两个不确定变量的情况进行说明，如图1所示。当珚R与S不干涉时，此时强度区间距离应力区间的远近，不符合Ben－Haim提出的非概率思想［9］。此时截尾随机变量的概率分布信息对最终可靠性度量结果无影响，可只取其上下界将其当作非概率区间变量，采用非概率可靠性指标珔η进行度量较为合适。而当珚R与S干涉时，采用珔η指标不合适，因为绝对安全已经不存在，只考虑最可能失效点一点的信息是不够的，应该考虑干涉域的信息，采用传统概率可靠性指标珋β是合适的，应当充分考虑截尾随机变量的概率分布信息。因而需要综合考虑这两种情况，即对应标准超球空间中，单位超球与极限状态曲面干涉与不干涉两种情况，如图1所示。

在文献［20］中，作者针对上述存在的干涉与不干涉两种情况提出多维超椭球凸集合可靠性综合指标定义，但极限状态函数中只包含多维超椭球凸集合变量，将其扩展到截尾随机变量与多维超椭球凸集合非概率变量同时存在的情况，则一种新的混合可靠性指标珔κ（珚X，Y）定义为

式中：珔η在非概率可靠性指标基础上发展而来；珋β由传统概率可靠性指标发展而来；Φ（·）为标准正态分布函数。

在文献［4］提出的混合模型的基础上，加入截尾随机变量的上下界约束，则得到珋β（珚X，Y）的表达式为

式中：G为标准正态空间中的极限状态函数；u为标准正态空间变量；uR与uL为的上下界；Δvj为第j个标准超球空间向量。sgn （））提取G （0，Δv）取值的正负号，确定搜索到的概率可靠性指标β珋（最短距离）的正负值。

η珔（X珚，Y）在非概率可靠性指标η 的基础上加入截尾随机变量，其表达式为

式中：Δv′为从截尾随机变量珚X转换来的等效标准超球空间向量；m为截尾随机变量个数；n为超椭球凸集合个数；δi为第i个截尾随机变量转化的等效区间变量；δj为第j个超椭球凸集合转化的等效区间变量。sgn（G（0，0））提取G 0，（）0取值的正负号，确定搜索到的非概率可靠性指标珔η（最短距离）的正负值。为了提高计算效率，方便迭代计算，可将珔η（珚X，Y）这一极小－极大值双层优化问题转换为标准超球空间中原点到极限状态曲面最短距离问题［20］，即

式中：G′为极限状态方程约束函数；C为权重系数，其涵义是加快中括号中“非概率可靠性指标只可能存在于无穷空间中通过原点与区间集合顶点的超射线上”这一必要条件迅速收敛于0。

2 混合可靠性指标求解步骤

由式（3）与式（5）可以看出，珋β（珚X，Y）与珔η（珚X，Y）均可采用与传统概率可靠性指标求解类似的改进的一次二阶矩法快速迭代求解，为保证迭代收敛性，采用改进的有限步长迭代法进行求解［20－21］。改进的有限步长迭代法具体求解步骤将不再赘述，只给出混合可靠性指标κ珔的求解过程。首先迭代求解η珔，若η珔≥1，则κ珔＝η珔；若η珔＜1，则迭代求解β珋，κ珔＝Φ（β珋）。下面给出η珔与β珋 的求解过程。

2．1 η珚的求解步骤

步骤1 只考虑截尾随机变量X珡i的上下界，将其转化为等效区间变量Y′i∈ ［］。再将Y′转化为标准超球空间变量Δv′i，即

步骤2 将多维超椭球凸集合向量Yj转化为标准超球空间向量Δvj，即

式中：Λj为对角矩阵；Pj为正交矩阵；且Wj＝为描述超椭球形状的已知正定矩阵；αj为确定超椭球大小的已知正实数。

步骤3 采用改进的有限步长迭代法求解珔η。

2．2 珔β的求解步骤

步骤4 令k＝k＋1，若 Δv（k＋1）－Δv（k）＋u（k＋1）－u（k）＜ε，则迭代循环终止；否则，返回步骤1。

3 混合可靠性基础上的优化算法

在上述给出的截尾随机变量与多维超椭球凸集合非概率变量同时存在的混合可靠性指标珋κ（珚X，Y）基础上，基于RIA法给出的优化模型为［18］

式中：d为设计向量；f（d）为目标函数；珔κj为第j个极限状态函数对应的混合可靠性指标约束允许值；gj（d，珚X，Y）为第j个极限状态函数；Rj（d，珚X，Y）为第j个极限状态函数对应的混合可靠性指标约束；珔κ［gj（d，珚X，珚Y）］为第j个极限状态函数计算得到的混合可靠性指标；hi（d）为确定性约束；dL和dU为设计变量的上下界；Ng为混合可靠性约束个数；Nh为确定性约束个数。

为了保证搜索到的最优值的全局性与快速性，将具有全局性的混沌优化算法与高效的局部优化算法Powell算法相结合，并对组合优化算法的搜索策略进行改进，以达到既保证全局性又具有搜索速度快的特点。在采用混沌－Powell优化算法搜索式（9）的混合可靠性优化模型时，需先用乘子法将约束优化转化为无约束优化模型［22］，即

式中：ψ（d）为无约束优化目标函数；r为系数；λ为乘子，设计变量的上下界约束可归到确定性约束中。乘子迭代公式为

文中采用均匀性较好的Skew－Tent映射式进行混沌搜索，其表达式为［23］

下面给出基于Skew－Tent映射式的改进搜索 后 的 混 沌－Powell（ST－Powell）优 化 算 法 对式（10）混合可靠性优化模型进行搜索的步骤。

步骤1 初始化参数，设置混沌运动最大次数N1，并置k＝k1＝k2＝0。赋n个微小差异的初值给Skew－Tent映射式（12）中的（不取不动点：0．25，0．50，0．75），则可由式（12）得到n个轨迹不同的混沌变量序列

2）若k≠0，则进行以下比较：若ψk＜（k1－1），则ψ1＊（k1）＝ψk，（k1）＝dk，进行步骤4；否则，进行步骤5。

步骤4 以混沌当前迭代步搜索得到的最优点d1＊（k1）为初始点进行Powell局部快速搜索得到最优值ψ2＊（k1）与最优点（k1）。

1）若k1＝0，则ψ＊（k2）＝（k1），d＊（k2）＝（k1）。

2）若k1≠0，进行以下比较：若（k1）＜ψ＊（k2），则ψ＊（k2）＝（k1），d＊（k2）＝（k1）。

3）置k1＝k1＋1，进行步骤5。

步骤5 置k＝k＋1，若k≤N，并由式（12）得到n个轨迹不同的新的混沌变量tk＋1i，返回步骤2。若k＞N1，则进行步骤6。

步骤6 若k2＞0∩ d＊（k2）－d＊（k2－1）＜ε，则ST－Powell算法搜索终止，输出最优值ψ＊（k2）与最优点d＊（k2）；否则，置k2＝k2＋1，并将当前最优值所对应的混沌变量加微小扰动作为下次混沌搜索的初值，即t0i＝t＊i＋δ，返回步骤1。

这里对全局性混沌优化算法与局部快速优化算法组合后的搜索策略进行了改进，目前组合算法的搜索策略是先由混沌搜索到一当前最优解，然后以当前最优解为初始点进行局部快速寻优［24］；而改进搜索策略后的ST－Powell组合算法是混沌变量每搜索到一改进解（此时混沌算法并未结束），即进行一次Powell算法局部搜索，相当于将Powell算法嵌入到混沌搜索中。下面以图2说明改进搜索策略后的ST－Powell优化算法在全局性搜索上的优越性。前一种搜索策略的不足在于混沌搜索由于局部搜索能力较弱得到的当前最优解很可能不是全局最优解，尽管混沌的遍历性保证混沌轨道点能到达过全局最优解附近（图2中E点和F点），但由于没能到达全局最优点（图2中A点），而最优解附近的函数值（图2中E点和F点）比局部最优值（图2中B点、C点和D点）小，则全局最优解附近点被局部最优点取代的可能性非常大，因而混沌搜索得到的最优解往往不是全局最优而是局部最优，以局部最优点进行局部快速优化算法搜索得到的也是局部最优点。这将大大降低组合优化算法全局性的搜索能力，若需要得到较好的全局寻优率，则需要大幅提升混沌运动次数，降低搜索效率。而改进搜索策略后的ST－Powell优化算法则很好解决了这个不足，每找到一混沌改进解就进行Powell算法局部搜索，加强了混沌搜索每一步的局部寻优能力，从而当混沌搜索到达全局最优附近时（图2中E点和F点），能通过Powell算法局部搜索到达全局最优（图2中A点），不会被局部最优（图2中B点、C点和D点）所取代，增大全局寻优率，提高了搜索效率。

改进搜索策略后的ST－Powell优化算法的全局搜索效果将在数值算例1中进行验证。另外在求解式（10）中目标函数最优值时将会用到第2节中介绍的混合可靠性指标求解步骤。由于在求解式（10）时是由乘子法将约束优化转为无约束优化模型，因而改进搜索策略后的ST－Powell优化算法与改进的有限步长迭代算法搜索混合可靠性基础上的最优值的流程如图3所示，其中Kcz为乘子法迭代步数，ζ为r的调节系数［22］。

4 数值算例

下面给出4个数值算例：算例1验证改进搜索策略后的ST－Powell优化算法的全局性；算例2验证文中提出的算法搜索混合可靠性基础上的最优值的正确性；算例3给出带有截尾随机变量与非概率变量的高非线性极限状态函数的混合可靠性基础上的优化搜索过程；算例4对飞行器上的执行机构电动舵机的关重件滚珠丝杆尺寸进行重量最轻的混合可靠性优化设计，以显示文中提出的混合可靠性指标及其基础上的优化算法在工程上具有较好的应用前景和适用性。

算例1 下面引用文献［24］的2个常用的全局性测试函数，其表达式为

f1有多个局部极小值，一个全局最优点（0，0，0），全局最优值为0。f2有几千个局部极小值，一个全局最优点（0，0，0，0，0），全局最优值为0。

表1与表2对比了改进搜索策略后的STPowell优化算法与文献［24］中的混沌－BFGS混合法对式（13）和式（14）的搜索结果。为测试优化算法的全局寻优率，随机给出100个混沌变量的初值，进行100次算法搜索，记录搜索到的全局最优值（i＝1，2）与最优点x＊、搜索时间Time及全局寻优率P（%），其中、x＊和Time为100次搜索中搜到的所有全局最优解的相应项相加取均值。

表1 f1函数的全局寻优结果Table 1 Global optimization results of function f1

表2 f2函数的全局寻优结果Table 2 Global optimization results of function f2

从寻优结果可以看出，改进搜索策略后的ST－Powell优化算法在较少混沌运动次数N1的情况下，全局寻优率却得到较大提升，表明改进搜索策略后的ST－Powell优化算法全局寻优性好、寻优速度快。

算例2 为验证改进搜索策略后的STPowell优化算法与改进的有限步长迭代法搜索混合可靠性基础上的最优值的正确性，采用文献［17］的算例进行验证，注意此时求解的混合可靠性指标是β（X，Y），X为无截尾区间的普通随机向量，不是文中提出的κ珔（X珚，Y）。算例的优化模型为

式中：

设计变量μ1和μ2分别为随机变量X1和X2的均值，X1和X2的标准差σ1＝σ2＝0．3。Y1与Y2采用凸集合描述为Y∈｛Y｜（Y－Y ）TWy·（Y－Y）≤1｝，其 名 义 值Y＝ ［Y珚1Y珚2］T＝标目标值βm，j＝3．0（j＝1，2，3）。

采用改进搜索策略后的ST－Powell优化算法与改进的有限步长迭代法相结合的搜索过程如表3所示，可以看出文中提出的算法与文献［17］的计算结果一致，说明了本文算法搜索混合可靠性基础上的最优值的正确性。同时本算法是由全局性与局部快速相结合的组合优化算法，并采用改进的有限步长迭代法（快速算法）求解混合可靠性指标，乘子法只进行3步即得到最优值，计算较快、耗时较少。

表3 算例2的最优值搜索过程Table 3 Search process of optimal value of Example 2

算例3 本算例的极限状态函数的非线性程度较高［19］，且极限状态函数中包含截尾随机变量与非概率变量，可靠性指标采用文中提出的混合可靠性指标珔κ，算例优化模型为

其中：μ1和μ2分别为截尾标准正态分布变量X1与X2的均值；X1和X2的标准差σ1＝σ2＝1．0；其 截 尾 区 间 为 X1∈ ［－0．9，0．9］与X2∈［－2．5，2 ．5］ ；Y1为区间变量，Y1∈ ［－1，1］。很显然函数f的最小值为0。

最优值的搜索过程如表4所示，迭代4步即得到最优值，表明算法搜索速度较快。表5与表6给出了μ1和μ2取最优值时，改进的有限步长迭代法求解η珔（X珚，Y）与β珋（X珚，Y）的迭代过程，可以看出对于高非线性极限状态函数算例，混合可靠性指标迭代求解时算法能得到收敛结果，且搜索速度较快。因为η珔（X珚，Y）＝0．903 0＜1，所以κ珋（X珚，Y）＝Φ（1 ．251 3）＝0．894 6。从 表6还可以看出，X1在迭代过程中受到截尾区间的约束。

表4 算例3的最优值搜索过程Table 4 Search process of optimal value of Example 3

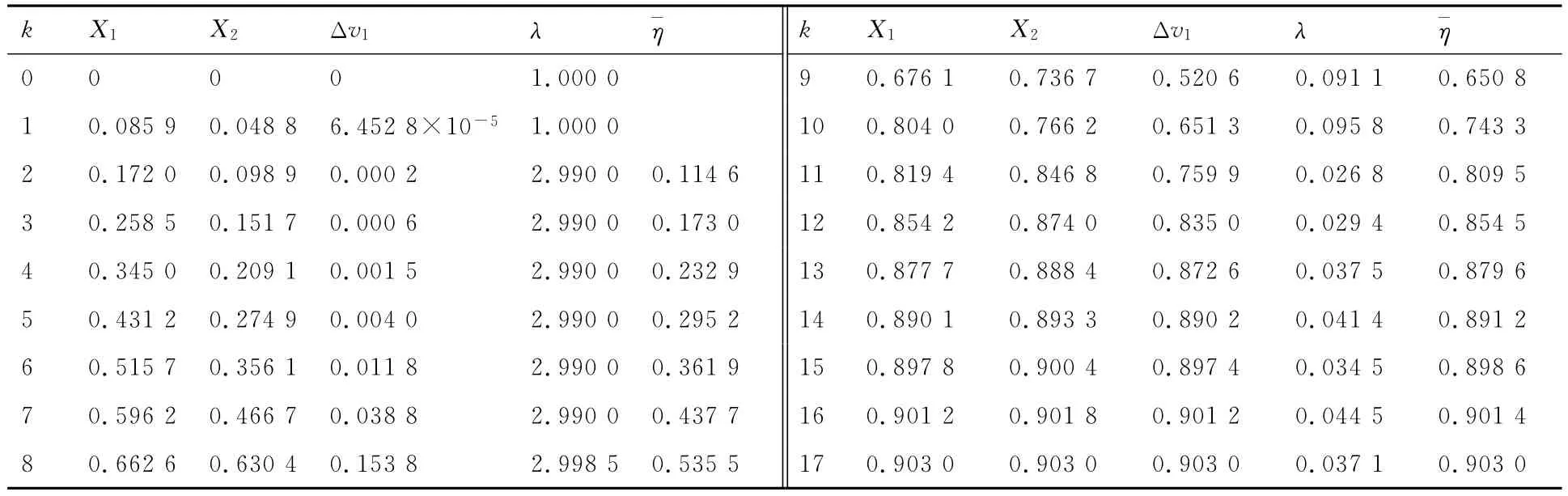
表5 珔η（珚X，Y）迭代过程列表Table 5 List of iterative process of珔η（珚X，Y）

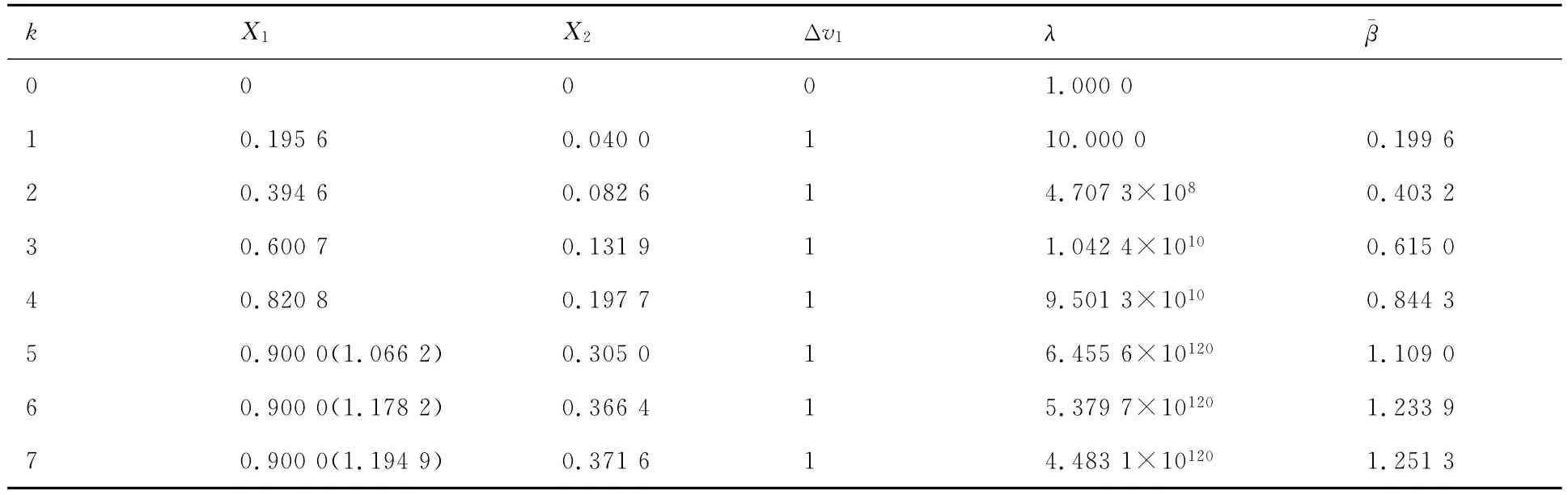
表6 珔β（珚X，Y）迭代过程列表Table 6 List of iterative process珔β（珚X，Y）

算例4 某型飞行器上电动舵机及其滚珠丝杆如图4所示。滚珠丝杆作为电动舵机重要的传动件，其主要有屈曲、转速过大和拉伸破坏3种失效模式。

下面给出以滚珠丝杆尺寸为设计变量，重量最轻为目标函数，3种失效模式对应的混合可靠度及设计变量范围作为约束函数的可靠性优化模型为

式中：d0为滚珠丝杆的公称直径；L为滚珠丝杆的长度；ρ＝7 800kg／m3为滚珠丝杆材料密度；W为滚珠丝杆的质量；珔κj为第j个极限状态函数对应的允许混合可靠度；gj为第j个极限状态函数。3个极限状态函数对应3种失效模式，其表达式为

式中：c为与丝杠支承方式有关的临界载荷系数；Mh为铰链力矩；Mj为惯性力矩；i2＝0．02为曲柄滑块机构减速比；f为与丝杠支承方式有关的临界转速系数；nmax为丝杠的最大转速；［］σ为丝杠的许用拉伸应力；d1＝d0－0．8为丝杠的内径，滚珠直径为0．8mm。从设计师处得知，式（20）中的系数、材料许用拉伸应力数据样本缺乏，不能得到它们的准确概率分布，但它们的范围能够得到，因而将系数c、f与［］σ处理为区间变量；所受力矩、最大转速可以通过充足的试验数据得到其准确的概率分布，且是有上下界的，即处理为截尾随机变量。从设计师处得到的工程数据确定式（20）中的不确定变量类型与取值如表7所示。

表8给出了滚珠丝杆尺寸的最优值搜索过程，图5给出了在尺寸取最优值情况下，屈曲、转速过大、拉伸破坏3种失效模式对应的混合可靠度计算迭代过程。从表8与图5可以看出，文中提出的算法很快就搜索到最优值，并且在迭代计算混合可靠度时，虽然前段出现振荡，但最终都能收敛。该算例的最优尺寸在尺寸区间的下限处获得。

算例5 结合工程设计需要与设计师要求，更改滚珠丝杆尺寸搜索范围并降低混合可靠度允许值，得到如式（21）所示的可靠性优化搜索模型。

表9给出了滚珠丝杆尺寸的最优值搜索过程，图6给出了在尺寸取最优值情况下，3种失效模式对应的混合可靠度计算迭代过程。此时d0在优化搜索区间内获得，L仍取下限值。

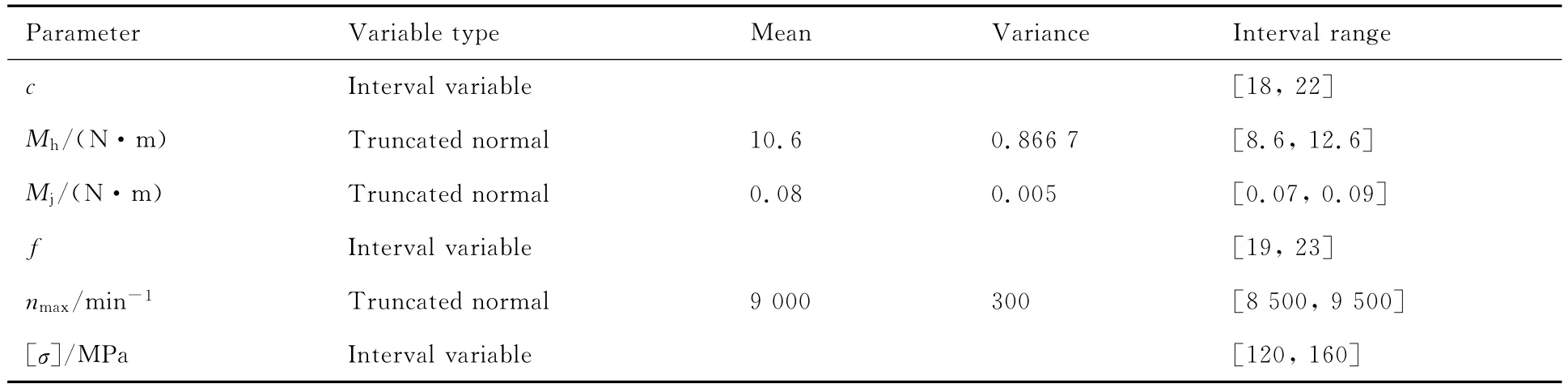
表7 电动舵机参数的不确定变量列表Table 7 List of uncertainty variables of electro－mechanical actuator parameters

表8 算例4的最优值搜索过程Table 8 Search process of optimal value of Example 4

表9 算例5的最优值搜索过程Table 9 Search process of optimal value of Example 5

5 结 论

1）文中提出的截尾随机－非概率变量混合可靠性模型能够适应在标准超球空间中极限状态曲面与单位超球干涉与不干涉两种情况。

2）改进搜索策略后的ST－Powell优化算法的全局寻优率得到较大提升，相应最大混沌运动次数却大幅下降，表明搜索速度也得到大幅提升。

3）改进搜索策略后的ST－Powell优化算法与改进的有限步长迭代法相结合能够正确搜索到混合可靠性基础上的最优值，且对于非线性程度较高的极限状态函数、工程结构算例同样适用。参 考 文 献

［1］ 王光远．工程软设计理论［M］．北京：科学出版社，1992：1－10．WANG G Y．Theory of soft design in engineering［M］．Beijing：Science Press，1992：1－10（in Chinese）．

［2］ 安伟光，蔡荫林，陈卫东．随机结构系统可靠性分析与优化设计［M］．哈尔滨：哈尔滨工程大学出版社，2005：15－20．AN W G，CAI Y L，CHEN W D．Reliability analysis and optimization design of random structure system［M］．Harbin：Harbin Engineering University Press，2005：15－20（in Chinese）．

［3］ VALDEBENITO M A，SCHUELLER G I．A survey on approaches for reliability－based optimization［J］．Structural ＆ Multidisciplinary Optimization，2010，42（5）：645－663．

［4］ LUO Y J，KANG Z，ALEX L．Structural reliability assessment based on probability and convex set mixed model［J］．Computers ＆ Structures，2009，87（21）：1408－1415．

［5］ QIU Z P，WANG J．The interval estimation of reliability for probabilistic and non－probabilistic hybrid structural system［J］．Engineering Failure Analysis，2010，17（5）：1142－1154．

［6］ DU X，SUDJIANTO A，HUANG B．Reliability－based design with the mixture of random and interval variables［J］．Journal of Mechanical Design，2005，127（6）：1068－1076．

［7］ 程远胜，钟玉湘，游建军．概率及非概率不确定性条件下结构鲁棒设计方法［J］．工程力学，2005，22（4）：10－14．CHENG Y S，ZHONG Y X，YOU J J．Structural robust design subject to probabilistic and non－probabilistic uncertainties［J］．Engineering Mechanics，2005，22（4）：10－14（in Chinese）．

［8］ ELISHAKOFF I．Essay on uncertainties in elastic and viscoelastic structure：From A．M．Freudenthal’s criticisms to modern convex modeling［J］．Computers ＆Structures，1995，56（6）：871－895．

［9］ BEN－HAIM Y．A non－probabilistic concept of reliability［J］．Structural Safety，1994，14（4）：227－245．

［10］ JIANG C，LONG X Y，HAN X，et al．Probability－interval hybrid reliability analysis for cracked structures existing epistemic uncertainty［J］．Engineering Fracture Mechanics，2013，112－113（11）：148－164．

［11］ YANG X F，LIU Y S，ZHANG Y S，et al．Probability and convex set hybrid reliability analysis based on active learning Kriging model［J］．Applied Mathematical Modelling，2015，39（14）：3954－3971．

［12］ WU D，GAO W，FRANCIS T L，et al．Probabilistic interval limit analysis for structures with hybrid uncertainty［J］．Engineering Structures，2016，114：195－208．

［13］ 王军，邱志平．结构的概率－非概率混合可靠性模型［J］．航空学报，2009，30（8）：1398－1404．WANG J，QIU Z P．Probabilistic and non－probabilistic hybrid reliability model of structures［J］．Acta Aeronautica et Astronautica Sinica，2009，30（8）：1398－1404 （in Chinese）．

［14］ 孙文彩，杨自春，唐卫平．随机和区间混合变量下结构可靠性分析方法研究［J］．工程力学，2010，27（11）：22－27．SUN W C，YANG Z C，TANG W P［J］．Structural reliability analysis based on random and interval mixed model［J］．Engineering Mechanics，2010，27（11）：22－27 （in Chinese）．

［15］ GE R，CHEN J Q，WEI J H．Reliability－based design of composites under the mixed uncertainties and the optimization algorithm［J］．Acta Mechanica Solida Sinica，2008，21（1）：19－27．

［16］ LUO Y J，ALEX L，KANG Z．Reliability－based design optimization of adhesive bonded steel－concrete composite beams with probabilistic and non－probabilistic uncertainties［J］．Engineering Structures，2011，33（7）：2110－2119．

［17］ 罗阳军，高宗战，岳珠峰，等．随机－有界混合不确定性下结构可靠性优化设计［J］．航空学报，2011，32（6）：1058－1066．LUO Y J，GAO Z Z，YUE Z F，et al．Reliability－based optimization design for structures with stochastic and bounded parameter uncertainties［J］．Acta Aeronautica et Astronautica Sinica，2011，32（6）：1058－1066 （in Chinese）．

［18］ XIA B Z，L H，YU D J，et al．Reliability－based design optimization of structural systems under hybrid probabilistic and interval model［J］．Computers and Structures，2015，160：126－134．

［19］ XIAO N C，LI Y F，YANG Y J，et al．A novel reliability method for structural systems with truncated random variables［J］．Structural Safety，2014，50：57－65．

［20］ 周凌，安伟光，贾宏光．超脱球凸集合可靠性综合指标定义与求解方法［J］．航空学报，2011，32（11）：2025－2035．ZHOU L，AN W G，JIA H G．Definition and solution of reliability comprehensivc index of super－ellipsoid convex set［J］．Acta Aeronautica et Astronautica Sinica，2011，32（11）：2025－2035（in Chinese）．

［21］ 周凌，贾宏光，安伟光．相关正态空间中改进的有限步长迭代法［J］．工程力学，2012，29（11）：137－142．ZHOU L，JIA H G，AN W G．Modified limit step length iteration algorithm in correlation normal space［J］．Engineering Mechanics，2012，29（11）：137－142（in Chinese）．

［22］ 陈卫东，蔡荫林，于诗源．工程优化方法［M］．哈尔滨：哈尔滨工程大学出版社，2006：100－110．CHEN W D，CAI Y L，YU S Y．Engineering optimization methods［M］．Harbin：Harbin Engineering University Press，2006：100－110（in Chinese）．

［23］ 江善和，王其申，江巨浪．一种新型SkewTent映射的混沌混合优化算法［J］．控制理论与应用，2007，24（2）：269－273．JIANG S H，WANG Q S，JIANG J L．Chaotic hybrid optimization algorithm of a new SkewTent map［J］．Control Theory ＆ Applications，2007，24（2）：269－273（in Chinese）．

［24］ 杨迪雄，李刚，程耿东．非线性函数的混沌优化方法比较研究［J］．计算力学学报，2004，21（3）：257－262．YANG D X，LI G，CHEN G D．Comparative study on chaos optimization algorithm for nonlinear function［J］．Chinese Journal of Computational Mechanics，2004，21（3）：257－262（in Chinese）．

Reliability－based optimization algorithm using hybrid model with truncated probability and non－probability

ZHOU Ling＊，LI Yanhui
Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China

A new hybrid reliability model is presented for the case that truncated probabilistic variables and non－probabilistic variables exist simultaneously in engineering．Based on the new hybrid reliability model and reliability index assessment（RIA）method，a nested loop hybrid reliability－based optimization model is also presented．Modified ST－Powell optimization algorithm with better search strategy is used to search the optimal values of design variables in the out－loop．Modified limit step length iteration algorithm，which can ensure convergence，is used to solve the new hybrid reliability index in the innerloop．Numerical examples show that the global optimization rate of the modified ST－Powell optimization algorithm with better search strategy can be promoted significantly，and the validity of hybrid reliability－based optimization model searched by the algorithm presented in this paper is proved．The algorithm can obtain the optimal values for hybrid reliability－based optimization model with high nonlinear limit state function．The algorithm presented in this paper has a good adaptability to hybrid reliability－based optimization problems of engineering structure．

truncated probabilistic variable；non－probabilistic variable；hybrid reliability model；modified ST－Powell optimization algorithm with better search strategy；modified limit step length iteration algorithm；reliability－based optimization

2016－03－11；Revised：2016－05－15；Accepted：2016－08－12；Published online：2016－08－26 10：05

URL：www．cnki．net／kcms／detail／11．1929．V．20160826．1005．002．html

s：National Natural Science Foundation of China（51305421）；National Defence Technology Basis Research Project of China（JSZL2014130B005）；Young Scholars Fund of Development Project of Science and Technology of Jilin Province（20140520137JH）＊Corresponding author．E－mail：hszl007＠163．com

V215．7；O213．2；TB114．3

A

1000－6893（2017）01－220216－13

http：／hkxb．buaa．edu．cn hkxb＠buaa．edu．cn

10．7527／S1000－6893．2016．0233

2016－03－11；退修日期：2016－05－15；录用日期：2016－08－12；网络出版时间：2016－08－26 10：05

www．cnki．net／kcms／detail／11．1929．V．20160826．1005．002．html

国家自然科学基金 （51305421）；国防技术基础科研项目 （JSZL2014130B005）；吉林省科技发展项目青年基金 （20140520137JH）

＊通讯作者 ．E－mail：hszl007＠163．com

周凌，李艳辉．基于截尾概率－非概率混合模型的可靠性优化算法［J］．航空学报，2017，38（1）：220216．ZHOU L，LI Y H．Reliability－based optimization algorithm using hybrid model with truncated probability and non－probability［J］．Acta Aeronautica et Astronautica Sinica，2017，38（1）：220216．

（责任编辑：徐晓）