Dryden型大气紊流对平流层飞艇能量最优轨迹影响

郑黎明，杏建军，陈子昂，王祎，于洋

Dryden型大气紊流对平流层飞艇能量最优轨迹影响

郑黎明，杏建军＊，陈子昂，王祎，于洋

中南大学 航空航天学院，长沙 410083

研究了常值风场作用下平流层飞艇的上升段轨迹优化和大气紊流对最优轨迹的影响问题。首先基于平流层飞艇的受力分析，建立了考虑常值风场、地球自转和飞艇质量变化等诸多因素的三自由度动力学模型，处理参数得到归一化的系统方程；其次采用直接配点法将平流层飞艇的最优轨迹问题转换为非线性规划问题，以最小能量为目标函数，给出非线性规划问题的求解策略，优化得出可行解后对飞艇的最优上升轨迹及相应的加速度项进行了分析，将优化的控制量代入微分方程验证了优化轨迹的准确性；最后加入Dryden型大气紊流的干扰，选取多组大气紊流干扰下的数据进行对比分析，仿真结果表明大气紊流叠加风场均值与飞艇终端位置误差存在一定规律，分析并提出了平流层飞艇抵御大气紊流干扰的策略。

平流层飞艇；轨迹优化；直接配点法；非线性规划；Dryden型大气紊流

平流层飞艇作为一个承担多元化任务的浮空器平台，相比于其他航空器和航天器在某些领域具有巨大的优势［1］，低耗能和长航时的工作特性使其成为国内外航空航天领域研究的热点［2］。平流层飞艇的工作环境为大气环境相对稳定的平流层［3］，适合飞艇的定点驻留和低速飞行，但是对于巨型低速的飞艇而言，穿越对流层时必然要面对恶劣的空间环境，受到各种干扰带来的负面影响［4］，为了让飞艇迅速而稳定到达平流层空间，开展平流层飞艇的轨迹优化势在必行。

目前，面向平流层飞艇轨迹优化的研究文献较少，Lee等［5－6］在韩国高空飞艇 VIA－200的基础上进行平流层飞艇上升段最优轨迹的研究，考虑湍流作用下根据三自由度模型求得最小时间和最小能量的最优轨迹，并基于最优轨迹研究非线性路径跟踪控制；Mueller等［7］针对最小时间和最小能量两种情况评估了时间和能量的经济性，研究不同起飞位置对飞艇最优轨迹的影响；Guo和Zhu［8］通过对飞艇热力学模型的建立，综合分析热力学效应对于飞艇最优轨迹的影响，但是轨迹优化问题中仅考虑常值风场作用，并未考虑随机风场对于最优轨迹有何影响。

实际飞行过程中，飞行器不仅受到常值风的作用，更会因为大气紊流的影响而导致飞行器飞行性能和品质下降，甚至难以正常飞行。大气紊流是指叠加在平均风上的连续随机脉动，赵震炎等［9］利用电子计算机产生复合Dryden模型的三维大气紊流信号，并对飞行模拟器如何使用该数学模型提出一些看法；吉洪蕾等［10］发展了一种适用于直升机飞行力学分析的三维空间大气紊流模型，并分析大气紊流对直升机飞行品质的影响；Dogan和Lewis［11］针对空中加油机综合考虑了常值风场，涡流风场以及大气紊流干扰等综合因素，通过对多种大气紊流干扰下飞机之间的相对位置、相对速度等相关飞行数据分析验证风场建模技术。飞艇作为巨型低速的浮空器，受到大气紊流干扰的负面影响更为显著，产生的扰动速度会使得飞艇无法按照预定轨迹到达目标位置。在目前公开的文献中，针对大气紊流对飞艇最优轨迹影响的文献较少，找出大气紊流对飞艇飞行轨迹的影响并给出飞艇抵御大气紊流干扰的策略，对于平流层飞艇放飞后能够精确地到达目标位置具有重要意义。

本文基于平流层飞艇的三自由度模型，采用直接配点法将轨迹优化问题转换为非线性规划（NLP）问题，求解出飞艇上升段能量最优轨迹；分析结果表明风场对于能量最优轨迹影响显著，而综合考虑常值风场和Dryden型大气紊流的复合作用，更接近于飞艇的真实飞行环境；最终基于优化结果中的控制输入，计算常值风场与复合风场作用下轨迹的终端误差并对比分析，找出规律并提出平流层飞艇抵御大气紊流干扰的策略。

1 平流层飞艇三自由度模型

1．1 基本假设

1．1．1 姿态稳定可控假设

在现有的关于平流层飞艇研究中，假设平流层飞艇为具有纵向对称平面的刚体，体积中心与浮力中心重合，体积中心与重心均在纵向面内且重心位于体积中心的正下方［1］。

所研究的飞艇模型主要参考韩国高空飞艇VIA－200的模型参数［5］，该飞艇通过矢量发动机和三角形尾翼的舵面系统完成飞艇的质心位置和姿态系统控制，推力和舵面系统如图1所示，其中μmax和εmax分别为矢量发动机转动过程中在艇身纵向面和横向面允许转动的最大角度。

研究内容为飞艇的轨迹优化问题，仅考虑质心位置变化，故默认飞艇的姿态稳定可控且整个飞行动力系统可提供该优化问题中的4个控制输入量：矢量发动机推力T和转角μ、迎角α、航向角ψ，有关航向角ψ作为控制量的解释将在下文飞艇三自由度动力学模型建立后给出。

1．1．2 滚转角为零假设

考虑飞艇的工作原理和任务特性，此处采用飞艇滚转角为零的假设，原因如下：

1）传统飞行器如飞机在实现横侧向的机动时需要倾斜机身产生一定的滚转角，而巨型低速的飞艇气动升力较小，通过改变滚转角完成横侧向机动收益过小。同时，飞艇可通过矢量发动机的推力T和横向面转角ε实现侧向力FL的控制，能够更有效地实现横侧向机动。

2）飞艇的优势在于能够实现低耗能长航时的对地定点观测任务，一般携带载荷为高分辨率观测器件，滚转角过大变化会影响飞艇对地观测任务的执行。

3）在文献［5］的轨迹优化研究中，并未采取滚转角为零的假设而是作为一个优化问题状态量处理，最终优化结果中滚转角几乎全程处于0°附近变化且最大值未超过5°。

1．1．3 静浮力假设

不同于传统的飞行器，飞艇在低速飞行中产生的气动升力远小于飞艇的重力，主要依靠巨大体积获得的浮力来平衡重力。在飞艇的初步设计阶段应该考虑飞艇受到的浮力能够通过压力调节系统调节而大于、等于或者小于重力，定义系数ζ为飞艇浮力B与重力G之差与飞艇的重力之比，即

系数ζ在较小范围内变化，本文选取ζ＝0，认为飞艇上升过程中浮力与重力始终平衡，即静浮力假设。将飞艇浮力与重力的方程代入式（1），可得到飞艇质量m（t）与质量变化率m（t）的表达式为

式中： 为飞艇体积；ρ（h（t））为飞行过程的大气密度；h（t）为飞艇的高度。

1．2 运动学模型

建立3个坐标系（见图2和图3）描述飞艇的运动：地心惯性坐标系OIJK［12］、北天东坐标系Onenu和速度坐标系Owxwywzw，在地心惯性坐标系中用飞艇距离地面的高度h，经度l和纬度λ来描述飞艇的质心位置，地球自转角速度为we，则飞艇的惯性速度VI可以表示为

式中：向量VL为北天东坐标系下的当地速度；V、W和E分别为飞艇空速、风速和地球自转速度。

飞艇在惯性坐标系的位置矢量r在Onenu中为

则惯性速度为

式中：R为地球半径；Ω为北天东坐标系Onenu相对于地心惯性坐标系OIJK的转动角速度，即

由图3可知，飞艇的航迹角γ和航向角ψ可描述北天东坐标系和速度坐标系之间的关系，其转置矩阵R满足

式中：x、y和z分别为速度坐标系x方向、y方向和z方向的矢量；e、n和u分别为北天东坐标系东西方向、南北方向和高度方向的矢量。

将式（4）中所有速度矢量转置于Onenu系中得到飞艇空速、风速以及地球转速的表达式并代入式（4）中，即可得到飞艇的运动学方程为

式中：WE为东西向风场速度；WN为南北向风场速度。

1．3 动力学方程

由牛顿第二定律知飞艇的动力学方程为

质量M为飞艇质量与附加惯性质量和，其表达式为

式中：mair为飞艇排开周围空气的质量；k1、k2和k3为附加惯性质量系数，可通过飞艇的外形尺寸确定［13］

通过对惯性速度VI的导数展开并整理得到其表达式为［7］

1．4 受力分析

飞艇所受到的力有重力G、浮力B、矢量发动机推力T和侧向力FL、气动升力L和阻力D。考虑飞艇在上升过程中重心位置随着质量变化而改变，此处选取浮心为受力作用点，其中重力、发动机推力和侧向力相对于浮心均有一定的力矩作用，会影响飞艇的姿态，但在该轨迹优化问题采用的是飞艇的质点模型，默认飞艇的姿态系统稳定可控，即上述力矩产生的影响可通过飞艇的舵面系统消除。

最终选取浮心为受力作用点，得到飞艇在纵向平面的受力如图4所示，各力均表示于速度坐标系中，即

式中：向量F为飞艇所受外力；向量L、D、T、G和B分别为速度坐标系中升力、阻力、推力、重力和浮力的表达式。

飞艇在横侧向平面仅有侧向力的作用，其大小的控制可以通过矢量发动机推力与横向面转角ε获得，其表达式为

飞艇上升过程中随着高度的增加，大气密度ρ（h（t））变化较大，必须考虑飞艇的质量变化率m（t）对飞艇的影响，此处引入反作用力FA描述飞艇质量变化产生的影响［14］，假设从飞艇气囊放出的气体速度与飞艇空速大小相等，方向相反。如图5所示，取飞艇质量变化间隔时间dt，气体质量为－dm，速度为－V，则飞艇质量为m（t）＋dm，速度为V＋dV，由动量守恒可知：

忽略二阶小项dmdV，则作用于x方向的合力∑Fx满足

综合考虑式（10），根据之前假设放出的气体速度与飞艇空速大小相等，方向相反且飞艇质量变化率为负值，故反作用力FA的方向指向x正方向，大小为FA＝m（t）V。为了便于计算飞艇的质量变化率，采用多项式拟合的方法来表示大气密度，其表达式为

式中：珔h＝h／hc，hc为高度的归一化常数。

联立式（10）、式（12）、式（13）和式（16）即可得到飞艇的三自由度动力学模型：

其中航向角变化率ψ表达式中包含可控侧向力FL，故将航向角ψ由状态变量转换为系统的可控输入，其上下界和变化速率受到系统约束。

1．5 气动力与风场模型

飞艇飞行过程中的气动升力和阻力的表达式为

式中：S＝2／3为参考面积；CL和CD分别为升力系数和阻力系数。这3个参数可通过风洞试验、CFD仿真［15］和半经验公式［16］获取，此处系数采用韩国VIA－200飞艇风洞试验数据拟合而成，其大小仅随飞艇迎角α变化［5］，即

风场的模型采用多项式拟合得到的HWM93常值风场模型［7］，表示为东西方向和南北方向，其大小仅随高度h变化，便于描述风的强度与梯度对飞艇上升轨迹的影响。

1．6 归一化处理

为了提高优化问题中的计算精度和运行效率，需对变量进行归一化处理。给出归一化常数k＝20，针对速度、时间、高度、加速度、力和密度定义归一化常数为

归一化常数数值和飞艇参数在附录B的表B1中给出，基于飞艇的运动学方程式（9）和动力学方程式（18）得到归一化的系统方程，包含4个控制输入和5个状态变量：

2 最优轨迹问题的转换与求解策略

2．1 基于直接配点法的问题转换

求解平流层飞艇上升段最优轨迹，即寻找控制变量u（t）使在时间［t0，tf］上目标函数J（x（t），u（t），t）取极小值。本文采用直接配点法［17］，在时间域［t0，tf］上离散状态变量x（t）与控制输入u（t），将轨迹优化问题转换为NLP问题。

现于时间域［t0，tf］选取 N 个节点，即有tk＝t0＋τktf，需要优化的变量数目为9 N＋1，表示为

通过直接配置法，将求解目标函数J（x（t），u（t），t）取得极小值的问题转换为J［X］取极小值的NLP问题。

2．2 目标函数选取

平流层飞艇的理想工作环境为高度h＝18～50km的广大平流层区域，在上升过程更少的能源消耗有助于延长飞艇的驻空时间，故选取能量最小性能指标为

考虑飞艇的迎角α、发动机转角μ和航向角ψ这3个控制输入所消耗能量属于姿态控制系统，此处选取矢量发动机推力T作为能量最优轨迹参考量。

2．3 系统约束条件

系统约束条件包含初值和终端约束，过程约束，控制变化率约束和变量上下界约束。

1）初值和终端约束。飞艇从起始位置放飞，最终到达目标位置，详细数值在仿真中给出，同时要求飞艇到达终端位置的当地水平速度VLf＝10m／s，满足表达式

2）过程约束。飞艇飞行过程中通过压力调节系统从气囊充放空气保持浮力与重力平衡，其系统调节能力受到一定限制，因此飞艇高度变化率受到压力调节系统的约束；同时飞艇正常飞行时总功率不能超过总体系统最大功率

3）控制变化率约束。控制输入的变化速率不能过大，需满足一定约束条件

4）变量上下界约束。所有变量的上下界约束如表1所示。

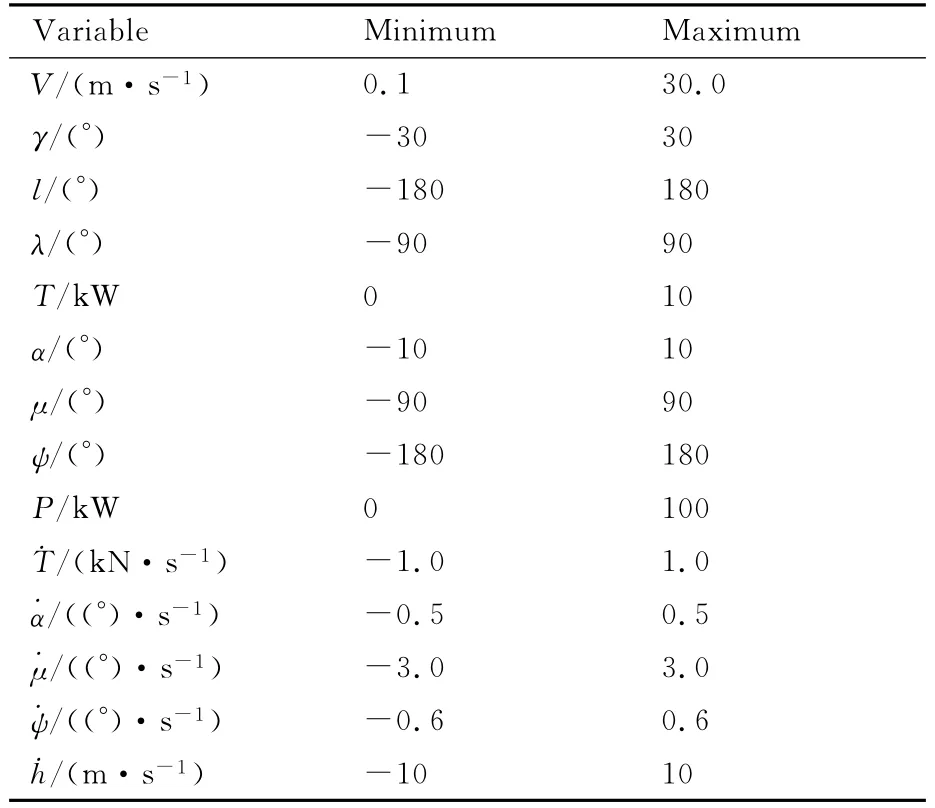
表1 变量上下界Table 1 Bounds of variables

2．4 NLP问题的求解策略

采用直接配点法求解最优轨迹时，为了提高计算的精度，需要选取更多的节点，而节点数目的增加势必会造成决策变量数目迅速增加［18］。本文采用序列二次规划（SQP）算法对NLP问题进行求解，需要给出优化问题的猜测初值，当节点数目过多且猜测初值选取不好时，很难甚至无法得到可行解，针对该问题提出以下3种求解策略：

1）对优化变量进行归一化处理，使得所有待优化变量集中于相近数量级，可以提高求解精度和运行效率。

2）采用较少的节点数目（N＝10）进行预优化，再得到初步可行解后通过插值处理得到多节点数（N＝20，40，60）情况下的迭代初值，重复此过程直至获得较多节点数目（N＝60）情况下的猜测初值。

3）设置低精度的截断误差获得初步可行解，然后逐步提高截断误差的精度，将获得的可行解作为初值代入，直至获得较高精度的猜测初值。

3 优化求解与模型验证

3．1 优化初值猜测

本文使用的SQP算法是一种局部优化算法，其优化结果依赖于初值的猜测，因此无法避免的收敛到局部最优解。目前解决该问题的方法一般有两个，一是根据工程经验直接判断该可行解是否为全局最优解；二是通过全局优化算法进行检验。

在使用全局优化算法（遗传算法）进行初值搜索时，仅选取节点数N＝10仍较难获得有效初值，且时效性很低；因此在该优化问题的初值猜测中，除了考虑2．4节中提到的NLP问题求解策略，仍需针对不同目标函数场景综合飞艇的动力学方程在理论上选取出较恰当的初值。例如在该最小能量问题的优化过程中，需考虑以下因素：

1）关注飞艇的总飞行时间tf变化，因为对于该优化问题只能确定飞行时间下限为2 133．4s（由高度变化率限制）且在系统约束条件中大部分方程均包含此项，因此必须密切关注tf变化，尝试较大范围的初值选取。

2）最小能量问题中以推力为参考量且假设飞艇浮力始终等于重力，故对于推力和飞艇空速的初值估计不宜过大；对于飞艇的放飞起点与目标位置，存在较大范围的经度差和高度差，纬度不变，综合考虑此情况中风场作用可能强于推力的作用，故预估整个飞行过程中纬度不变，经度和高度数值用简单的线性插值作为初值；飞艇的高度变化率h＝Vsinγ且飞行过程中高度应递增，故航迹角应选取正值才能实现升空。

通过采用2．4节提到的NLP问题的求解策略以及针对最小能量场景理论初值的猜测，较好地解决了该优化问题的初值猜测问题。

3．2 仿真场景选取

飞艇的放飞场景中存在自西向东的较强风场，为使飞艇消耗更少能量到达目标位置，选取距离终点正西方向250km的位置作为放飞地点，飞行过程中飞艇始终顺风而行，其初值和终值如表2所示，具体飞艇尺寸参数见附录B的表B1。

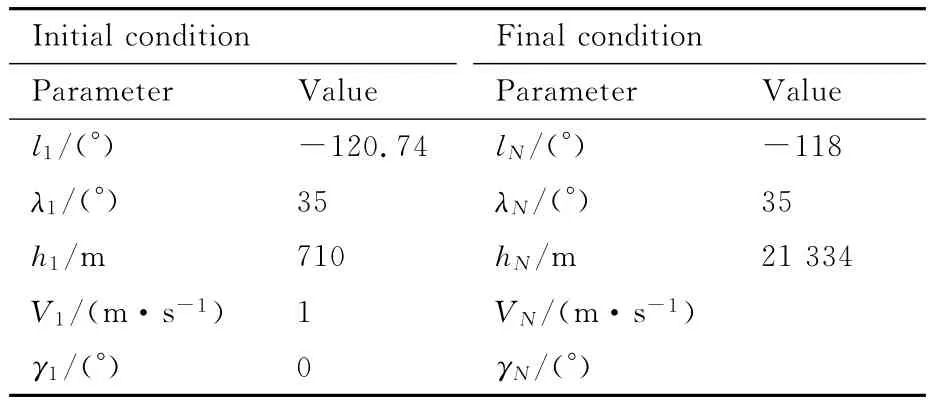
表2 仿真初值与终值Table 2Initial and final values of simulation

3．3 优化数据分析

3．3．1 仿真时效性分析

仿真计算在PC机上进行，CPU为Inter?2．90GHz，基于MATLAB环境的Fmincon函数对该NLP问题进行求解。该优化问题由于采用N＝10时获得的可行解并插值得到N＝20的初值，然后依次增加节点数并将前一次可行解插值作为更多节点数的初值，保证了仿真的时效性。如表3所示即为不同节点数优化所需时间。

在最小能量场景下，选取节点数N＝20时已经能够获得较高精度的可行解，与N＝40，60对比，3条状态曲线趋势和节点数值误差很小，通过一定插值处理后得到的初值已经很接近于可行解，所以能够快速的收敛，所用时间更少，虽然此时4个输入量的曲线仍有较大范围波动，但整体数值偏小，对状态量几乎无影响。

表3 不同节点所需时间Table 3 Running time for different numbers of nodes

3．3．2 能量最优轨迹

仿真选取节点数N＝20，40，60进行对比分析，结果如图6和图7所示。由表2中给出的仿真初值可知，飞艇在放飞后到达目标位置要完成高度方向约20km的高度差以及东西方向250km的经度差（南北方向初值与终值相同且受到较弱的风场影响），现就2个方面分析飞艇能量最优轨迹的可行解：

1）高度方向。由图6可知，整个飞行过程中飞艇的空速V 较小，最大值仅为5．06m／s，远低于优化中设置的上界30m／s，这是由于在能量最优轨迹中发动机推力T极小（如图7所示），以较长的飞行时间为代价节省了能量，用时4．47h；但是航迹角γ却几乎全程为最大值30°，保证了飞艇的高度上升（h＝Vsinγ），整个飞行过程中高度变化率h虽然数值较小（如图8所示），但是通过较长时间的积累作用完成了约20km的高度差。

2）东西方向。飞艇东西方向速度为VE＝Vcosγsinψ＋WE，其组成分别为空速分量Vcosγsinψ和东西风场项WE，其数值大小如图9所示，可以发现东西风场项占有较大比重，飞艇在静浮力的情况下主要借助于自西向东的常值风场完成250km的经度差。综上所述，在静浮力的条件下，飞艇在高度方向主要依靠较长时间的速度积累，在东西方向主要依靠东西向常值风场，最终从放飞点到达目标位置。同时由图7可知能量最优轨迹中发动机推力极小，风场对于飞行轨迹的影响显著，在实际飞行过程中由于风场的复杂性和随机性，会使得飞艇偏离预定的飞行轨迹而无法到达目标位置，这也是后文研究大气紊流对能量最优轨迹影响的意义所在。

3．3．3 加速度项分析

3．4 模型验证

为了验证优化结果的可行性，选取节点数目N＝60时控制输入代入三自由度模型积分得到对应的状态参数曲线，与优化所得最优轨迹状态参数曲线进行对比验证，两条曲线几乎完全一致。

4 大气紊流对飞艇最优轨迹的影响

4．1 Dryden大气紊流模型

作为巨型低速的浮空器，飞艇在飞行过程中受到风的干扰作用较大。在实际放飞过程中，不仅会受到常值风场的影响，更会因为大气紊流的干扰严重影响飞行品质。在飞行力学领域中研究飞行器对于大气紊流的响应时通常采用Dryden大气紊流模型［19］，本文采用 MATLAB／Simulink中Dryden大气紊流模块［20］进行仿真试验，其输入参数为飞艇的空速V，高度h以及转置矩阵R，输出参数为3个方向的线速度和角速度扰动。根据之前的基本假设，飞艇的姿态系统可通过矢量发动机和舵面系统控制，即飞艇姿态稳定可控，故只考虑大气紊流产生的3个线速度扰动对于飞艇质心位置的影响。

4．2 仿真分析

在3．4节的模型验证中，可知能量最优轨迹与数值积分曲线几乎完全一致，故基于能量最优轨迹分析飞艇对大气紊流的响应。

为便于数据对比分析，统计数据均选取最终高度h＝21 334m处数据进行采集（若最终时间未到达指定高度，则以当前高度记录），最终得到飞艇在无大气紊流和受到不同大气紊流干扰下的数据，详细统计数据见附录C。由于数据重合部分过多，故选取典型的4组场景与无大气紊流干扰场景绘制图形，如图11所示。统计飞艇飞行过程中受到3个方向常值风和大气紊流叠加风场的均值珚E、珡N和珡U，以及终端位置误差Δl、Δλ和Δh，如附录C中表C1所示。

假设飞艇在东西向飞行速度与风速相同，则可用东西向风场的均值来计算飞艇在时间t内沿东西向飞行的距离，得出经度计算误差Δl ，同理可得纬度计算误差Δ珓λ，均表示于附录C的表C2中。

将东西向计算误差与仿真误差进行对比，几乎每一组计算误差Δ珓l都比仿真误差Δl大0．1°数量级，这是由于飞艇在东西方向除了受到风的影响，还有地球自转项与反作用力项的综合作用。其中大气紊流3的情况下误差较大，原因是该情况下7 000s之前大气紊流产生高度方向的较大负值的线速度扰动，飞艇高度h几乎不变，故受到的东西向常值风较小，在7 000～16 000s内由于航迹角γ急剧增加，高度h和东西向均值风也随之增大，但是飞行的时间t较短，因此计算误差会相差较多。

由于南北方向的风场较弱，飞行过程中纬度几乎不变，但是能量最优情况下仿真时间偏长，会有累计误差。在未受到大气紊流的影响时，主要通过航向角ψ控制使其回到纬度35°的位置。此处计算误差Δ珘λ和仿真误差Δλ之间的差异主要是由于以下两个原因：

1）实际飞行过程不仅受到南北风的影响，还有推力和反作用力项的作用。

2）仿真过程的误差，验证过程按照给定的控制输入代入模型中，但是由于大气紊流的干扰，各状态量与理想情况均有差异，这种差异对风速较小的南北向影响尤为显著。

飞艇上升的高度项中含有飞艇空速分项Vsinγ和高度方向线速度扰动的叠加，因此对于高度h的分析较为复杂。一般情况下，若高度方向线速度扰动均值珡U为正值，则飞艇的高度变化剧烈，速率V会明显增大，二者的结合使得飞艇在较短时间内上升至高度h＝21 334m的位置，此时珡U起到正面主导作用（如大气紊流2）；若珡U为较大负值，则飞艇的升空难以实现，因为飞艇的高度h增加主要依靠飞艇空速分项Vsinγ长时间的累计作用到达目标点高度，较大负值的珡U与Vsinγ的叠加使飞艇上升困难甚至降落至地面，此时珡U起到负面主导作用（如大气紊流1）；若珡U为负值但数值较小时，仍会对飞艇的高度h有一定的影响，且空速分项Vsinγ会因为3个方向的线速度扰动而变化，使得飞艇最终高度h由这3项共同决定，有可能提前到达目标高度，也有可能低于目标高度（如大气紊流3和6）。

为了验证以上分析结果，另选取10组大气紊流干扰下的数据进行对比，如附录C中表C3和表C4所示，验证数据与分析结果体现了良好的一致性。

4．3 抵御大气紊流干扰的策略

根据以上分析，大气紊流对于飞艇的上升过程影响较大，为使飞艇能够抵御大气紊流干扰到达目标位置，需要对飞艇3个方向的实时位置误差进行控制。当终端时刻的位置误差趋近于0时，即认为飞艇可有效抵御大气紊流干扰。现通过终端时刻的位置误差控制阐述飞艇抵御大气紊流干扰的策略：

1）东西向 误差产生的主要原因是由于风场随机性，故需要在放飞飞艇之前对风场进行实时观测或者选择风场数据库较大的场地进行放飞，当风场的数据足够准确时，可以通过控制飞艇飞行时间t减小位置误差。

2）南北向 当飞艇自西向东飞行可通过控制侧向力FL（航向角ψ）来减小位置误差。

3）高度向 飞艇的高度项h会受到空速V，航迹角γ，紊流干扰ΔU的高度耦合作用，可通过改变飞艇浮力大小控制高度h的误差。

5 结 论

1）在求解非线性规划问题中，通过采用NLP问题求解策略以及在具体优化问题中的初值猜测方法，较好地解决了优化中对于猜测初值敏感的问题。

2）在飞艇的能量最优轨迹中，控制输入推力T极小，在高度方向主要依靠长时间的速度积累，在东西方向主要依靠常值风场的作用，以飞行较长时间为代价节省了能量，同时也说明了风场对于飞艇轨迹的影响显著，对加速度项的分析结果验证了上述结论。

3）根据常值风与大气紊流叠加风场均值计算飞艇终端误差并与仿真误差进行对比，找出两者之间规律并分析存在差异的原因，给出了飞艇抵御大气紊流的策略。

［1］ 李智斌，吴雷，张景瑞，等．平流层飞艇动力学与控制研究进展［J］．力学进展，2012，42（4）：483－493．LI Z B，WU L，ZHANG J R，et al．Review of dynamic and control of stratospheric airships［J］．Advances in Mechanics，2012，42（4）：483－493（in Chinese）．

［2］ LI Y W，NAHON M，SHARF I．Airship dynamics modeling：A literature review［J］．Progress in Aerospace Sciences，2011，47（3）：217－239．

［3］ 张礼学，王中伟．平流层飞艇环境适应性评价模型［J］．航空学报，2013，34（4）：719－726．ZHANG L X，WANG Z W．Environmental adaptabiity evaluation model for stratospheric airships［J］．Acta Aeronautica et Astronautica Sinica，2013，34（4）：719－726（in Chinese）．

［4］ 郭建国，周军．临近空间低动态飞行器控制研究综述［J］．航空学报，2014，35（2）：320－331．GUO J G，ZHOU J．Review of the control of low dynamic vehicles in near space［J］．Acta Aeronautica et Astronautica Sinica，2014，35（2）：320－331（in Chinese）．

［5］ LEE S，BANG H．Three－dimensional ascent trajectory optimization for stratospheric airship platforms in the jet stream［J］．Journal of Guidance，Control，and Dynamics，2007，30（5）：1341－1352．

［6］ LEE S，JANG J，RYU H，et al．Matching trajectory optimization and nonlinear tracking control for HALE［J］．Advances in Space Research，2014，54（9）：1870－1887．

［7］ MUELLER J B，ZHAO Y J，GARRARD W L．Optimal ascent trajectories for stratospheric airships using wind energy［J］．Journal of Guidance，Control，and Dynamics，2009，32（4）：1232－1245．

［8］ GUO X，ZHU M．Ascent trajectory optimization for stratospheric airships with thermal effects［J］．Advances in Space Research，2013，52（6）：1097－1110．

［9］ 赵震炎，肖业伦，施毅坚．Dryden大气紊流模型的数字仿真技术［J］．航空学报，1986，7（5）：432－443．ZHAO Z Y，XIAO Y L，SHI Y J．A digital simulation technique for Dryden atmospheric turbulence model［J］．Acta Aeronautica et Astronautica Sinica，1986，7（5）：432－443（in Chinese）．

［10］ 吉洪蕾，陈仁良，李攀．适用于直升机飞行力学分析的三维空间大气紊流模型［J］．航空学报，2014，35（7）：1825－1835．JI H L，CHEN R L，LI P．A model of three－dimensionalfield atmospheric turbulence for helicopter flight dynamics analysis［J］．Acta Aeronautica et Astronautica Sinica，2014，35（7）：1825－1835（in Chinese）．

［11］ DOGAN A，LEWIS T A．Flight data analysis and simulation of wind effects during aerial refueling［J］．Journal of Aircraft，2008，45（6）：2036－2048．

［12］ XING J J，TANG G J，CHENG W K，et al．Robust nonlinear control of spacecraft formation flying using constraint forces［J］．Science China Technological Sciences，2011，54（9）：2276－2282．

［13］ TUCKERMAN L B．Inertia factors of ellopsoids for use in airship design：NACA report No．210［R］．Washington，D．C．：NACA，1925．

［14］ MUELLER J B．Design and analysis of optimal ascent trajectories for stratospheric airships［D］．Minnesota：The University of Minnesota，2013．

［15］ 糜攀攀，孟军辉，吕明云．浮升混合飞艇气动性能及总体参数分析［J］．北京航空航天大学学报，2015，41（6）：1108－1116．MI P P，MENG J H，LYU M Y．Aerodynamic and overall parameters analysis of buoyancy－lifting hybrid air－ship［J］．Journal of Beijing University of Aeronautics and Astronautics，2015，41（6）：1108－1116（in Chinese）．

［16］ MUELLER J B，PALUSZEK M A，ZHAO Y J．Development of an aerodynamic model and control law design for a high altitude airship： AIAA－2004－6479［R］． Reston：AIAA，2004．

［17］ 雍恩米，陈磊，唐国金．飞行器轨迹优化数值方法综述［J］．宇航学报，2008，29（2）：397－406．YONG E M，CHEN L，TANG G J．A survey of numerical Methods for trajectory optimization of spacecraft［J］．Journal of Astronautics，2008，29（2）：397－406 （in Chinese）．

［18］ 张煜，张万鹏，陈璟，等．基于Gauss伪谱法的UCAV对地攻击武器投放轨迹规划［J］．航空学报，2011，32（7）：1240－1251．ZHANG Y，ZHANG W P，CHEN J，et al．Air－to－ground weapon delivery trajectory planning for UCAVs using Gauss pseudospectral method［J］．Acta Aeronautica et Astronautica Sinica，2011，32（7）：1240－1251（in Chinese）．

［19］ 肖业伦．Dryden大气紊流频谱的等价确定性函数及其在飞机相应问题中的应用［J］．航空学报，1986，7（2）：198－204．XIAO Y L．The equivalent deterministic function of the Dryden’s spectra of atmospheric turbulence and its application to the aircraft response problem［J］．Acta Aeronautica et Astronautica Sinica，1986，7（2）：198－204（in Chinese）．

［20］ CAMPBELL C W．A spatial model of wind shear and turbulence for flight simulation：NASA－TR－TP－2313［R］．Washington，D．C．：NASA，1984．

附录A：

风场梯度项和地球自转项的具体表达式为

附录B：

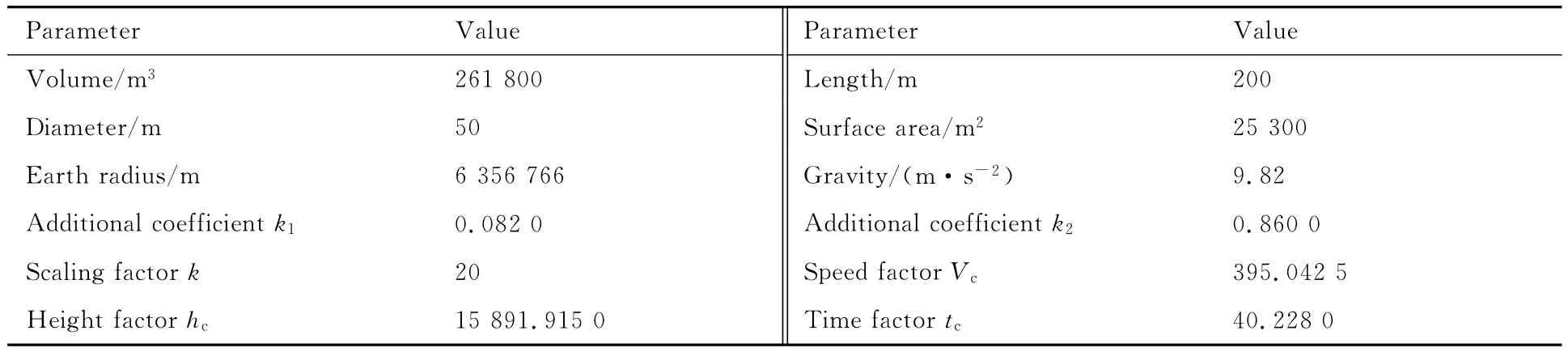
表B1 飞艇参数表Table B1 Parameters of airship

附录C：

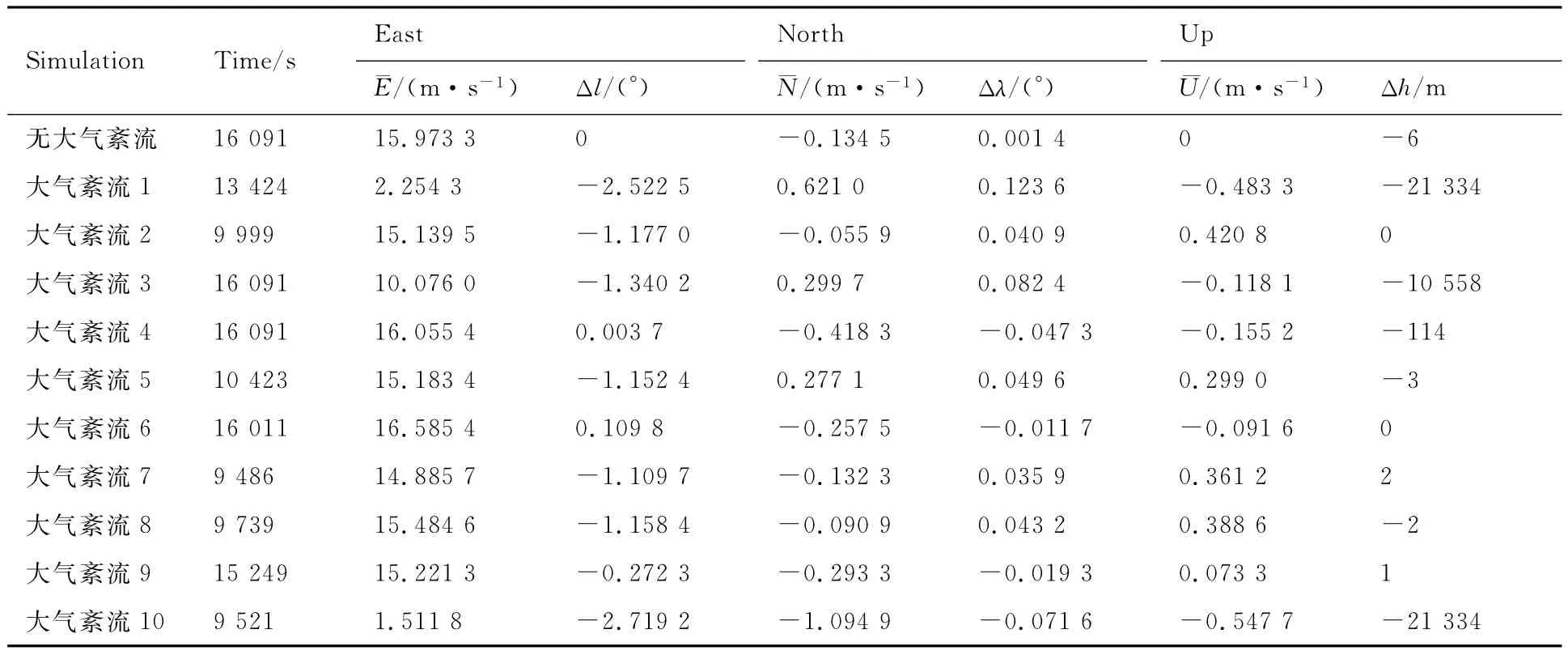
表C1 叠加风场均值与终端位置误差Table C1 Mean of complex wind and final position error

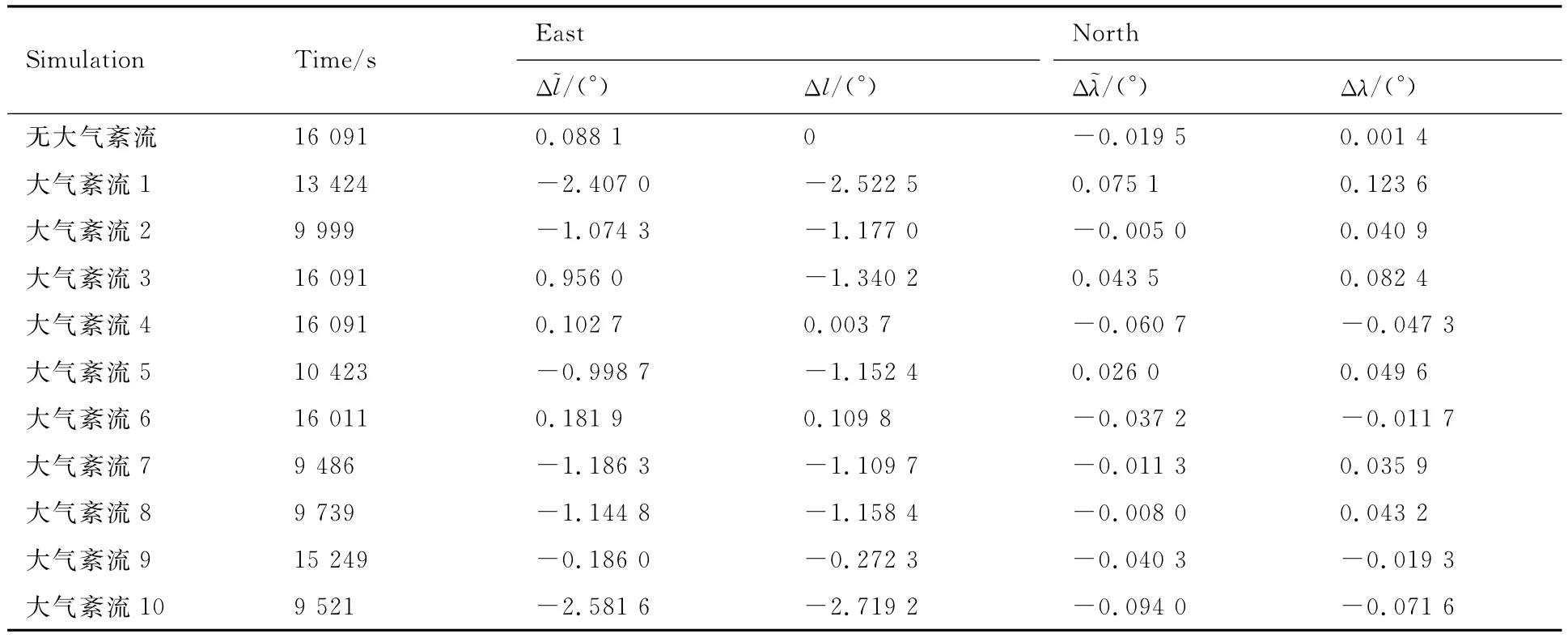
表C2 计算误差与仿真误差Table C2 Errors from calculation and simulation

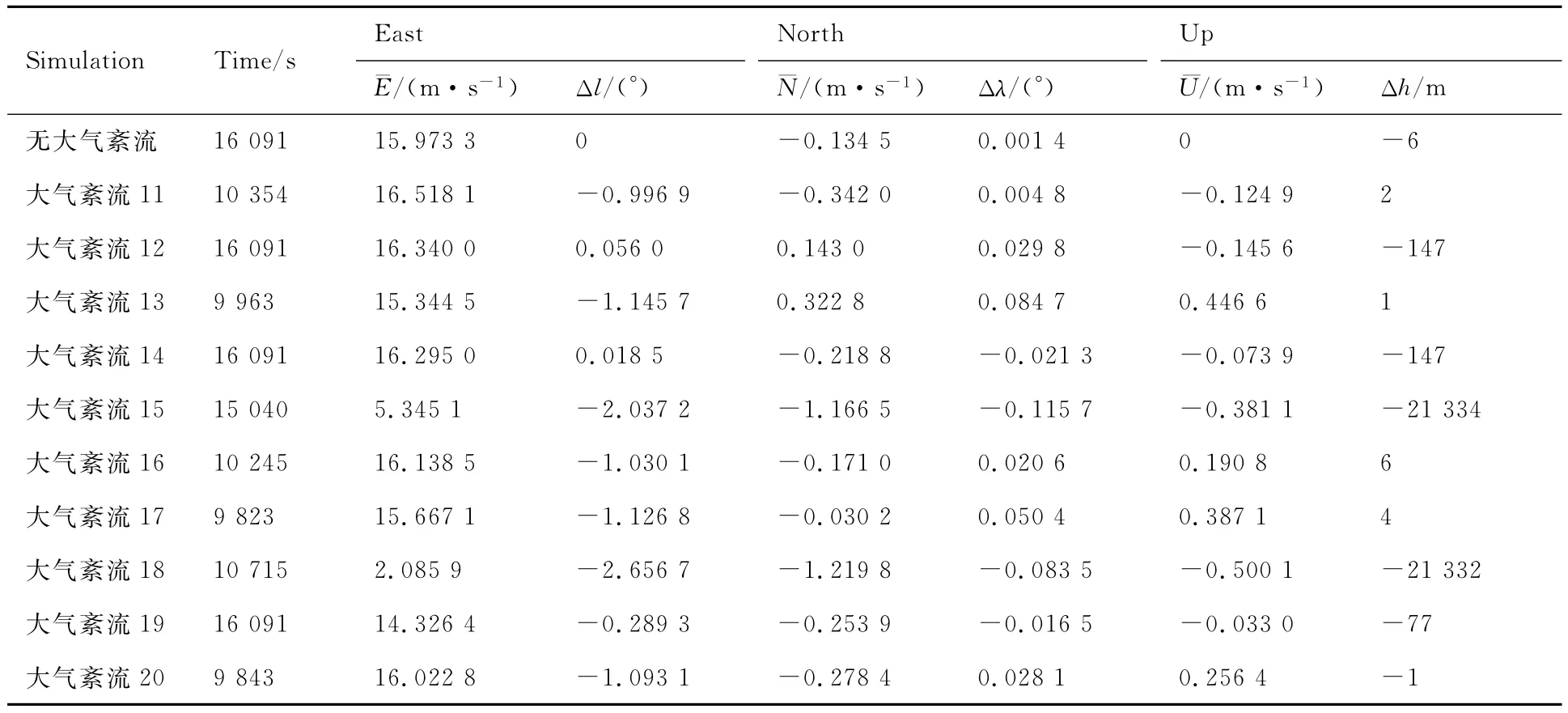
表C3 验证数据 （1）Table C3 Examination data（1）

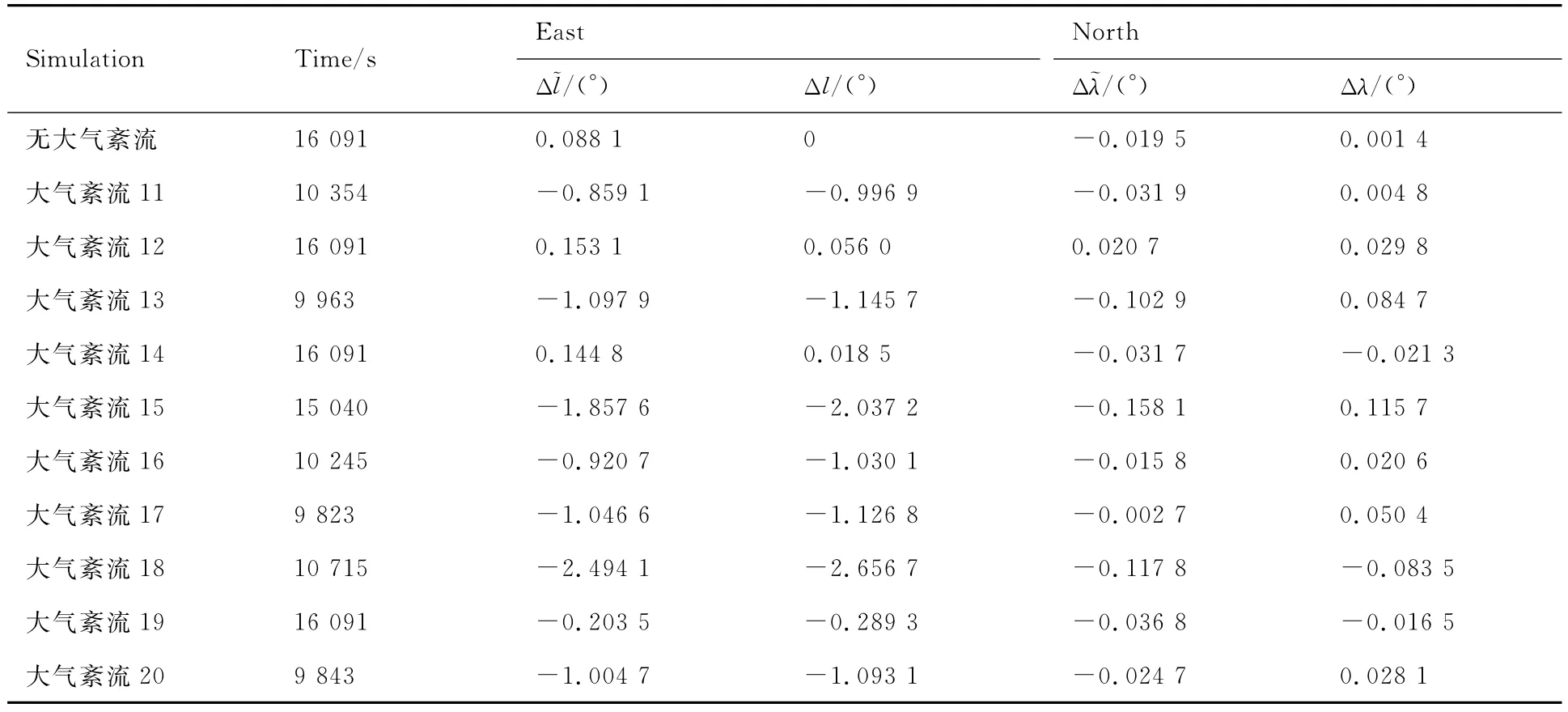
表C4 验证数据（2）Table C4 Examination data（2）

Effect of Dryden atmospheric turbulence on minimum－energy trajectory of stratospheric airships

ZHENG Liming，XING Jianjun＊，CHEN Ziang，WANG Yi，YU Yang
School of Aeronautics and Astronautics，Central South University，Changsha 410083，China

This paper investigates the ascent optimal trajectory of stratospheric airship with constant wind and the effect of atmospheric turbulence on optimal trajectory．First，three－degree－of－freedom dynamics model of stratospheric airship was completed by forces analysis，considering the constant wind，earth rotation，mass rate and other factors，and then the variables were scaled to obtain a normalized system equation．Second，this problem of optimal trajectory was transformed into a problem of nonlinear programming by using the direct collocation method．Considering the minimum energy scenario，an appropriate solution for nonlinear programming problem was determined，and the feasible solution was obtained．Then the control history of solution was taken into the system equation to examine the feasibility and the acceleration components were analyzed．Finally，the Dryden atmospheric turbulence was introduced to the minimum energy scene，and then the data of computation and comparison analysis were obtained．By discussing the error between calculation and simulation，the relation of the error of final position and the mean of complex wind was found，and a strategy for resisting the interference of Dryden atmospheric turbulence for stratospheric airships was raised．

stratospheric airship；trajectory optimization；direct collocation method；nonlinear programming；Dryden atmospheric turbulence

2016－03－02；Revised：2016－04－13；Accepted：2016－05－22；Published online：2016－05－26 11：37

URL：www．cnki．net／kcms／detail／11．1929．V．20160526．1137．004．html

s：China Postdoctoral Science Foundation（20080440217，200902666）

V19；V274

A

1000－6893（2017）01－120180－15

http：／hkxb．buaa．edu．cn hkxb＠buaa．edu．cn

10．7527／S1000－6893．2016．0157

2016－03－02；退修日期：2016－04－13；录用日期：2016－05－22；网络出版时间：2016－05－26 11：37

www．cnki．net／kcms／detail／11．1929．V．20160526．1137．004．html

中国博士后科学基金 （20080440217，200902666）

＊通讯作者 ．E－mail：xjj＠csu．edu．cn

郑黎明，杏建军，陈子昂，等．Dryden型大气紊流对平流层飞艇能量最优轨迹影响［J］．航空学报，2017，38（1）：120180．ZHENG L M，XING J J，CHEN Z A，et al．Effect of Dryden atmospheric turbulence on minimum－energy trajectory of stratospheric airships［J］．Acta Aeronautica et Astronautica Sinica，2017，38（1）：120180．

（责任编辑：鲍亚平）

＊Corresponding author．E－mail：xjj＠csu．edu．cn