藏在手机里的微型陀螺仪
刘延柱 杨晓东(上海交通大学工程力学系,上海200240)(北京工业大学机电学院,北京100124)
藏在手机里的微型陀螺仪
刘延柱∗,1)杨晓东†∗(上海交通大学工程力学系,上海200240)†(北京工业大学机电学院,北京100124)
叙述安装在手机内的各种微型振动陀螺仪及其力学原理.
振动陀螺仪,科氏惯性力,微机电系统
手机技术的飞跃式发展堪称奇迹.20世纪笨重的“大哥大”今日已大变样,成为人手一只不可替代的随身法宝.手机的功能早已不限于通话,它能写信、阅读、录音、拍照、摄像、上网、发文件、支付、看电视,几乎无所不能.留心一下还能发现,手机的不少功能与手机的姿态和运动有关.最常见的如手机的“摇一摇”功能,图像随手机转动的功能,拍照消除手抖的功能,提供水平面的功能,纪录走路步数的功能,老年人防跌预警功能等等.还有些不常用但更复杂的功能,如自主导航的功能.要实现这些功能,手机的姿态或角速度是必不可少的信息,它们是如何量测出来的呢?
在飞机或导弹等飞行器的导航系统里,量测姿态或角速度的核心元件是陀螺仪.传统陀螺仪就是一个旋转轴能自由改变方向的转子.转子高速旋转时可出现独特的动力学现象:无力矩作用时旋转轴在惯性空间中指向不变,有力矩作用时旋转轴朝力矩矢量的方向进动.陀螺仪的量测功能即来源于此动力学特性.如能将陀螺仪装在手机里,姿态或角速度的量测自然不成问题,但要实现这一想法却谈何容易.手机的体积比飞机和导弹缩小了何止千万倍,要在小小的手机里安装这种元件,首先要将陀螺仪的体积缩小千万倍.
幸运的是,20世纪60年代兴起的微机电系统MEMS(microelectromechanical systems)至今已发展成熟.所谓微机电系统,就是借助电子芯片的印刷蚀刻等特殊加工工艺,在硅基或金属基上制造各种微小的机械装置.采用这种技术,陀螺仪的缩微问题即迎刃而解[1].不过转子的动量矩随几何尺度的缩小以4次方比例减弱,而且高速旋转转子的缩微加工也难度太大.因此缩微成功的陀螺仪仅限于无转动部件的陀螺仪,即振动陀螺仪.

图1 音叉式振动陀螺
振动陀螺仪是一种非传统陀螺仪,它是利用质点振动因载体转动产生的科氏惯性力来确定载体的角速度.将图1所示音叉形装置固定在载体上,两臂的质量集中为两个质点 A和 B.激励音叉的两臂产生持续的振动,振型保持对称,A和 B的相对速度 vA和vB方向相反.当载体以角速度 ω转动时,质点 A,B上产生方向相反的科氏惯性力FA=−2mω×vA和FB=−2mω×vB,组成交变的力偶作用在音叉的立柱上,使其作扭转振动.其幅值与科氏惯性力成正比,也与载体角速度ω大小成正比.这种音叉式振动陀螺在自然界其实早已存在.苍蝇的后翅演化成的称为楫翅的小棒就是微缩的振动陀螺(图2).当楫翅以每秒 330次的频率作对称振动时,苍蝇就能在飞行中感知自身的转动角速度,判断飞行的方向.

图2 苍蝇的楫翅
比音叉构造更简单的振动陀螺是一个由弹簧支承可沿x轴和y轴两个方向振动的单个质点(图3).对质点沿x轴施加与固有频率ν接近的周期激励,使质点维持接近谐振的周期运动.当载体绕z轴转动时,产生沿 y轴的科氏惯性力,使质点出现沿 y轴的振动,振幅与载体角速度ω大小成正比[2].这种装置由于构造简单,更适合微缩加工,制造出的微型陀螺元件可缩小到毫米尺度(图4).

图3 质点式振动陀螺
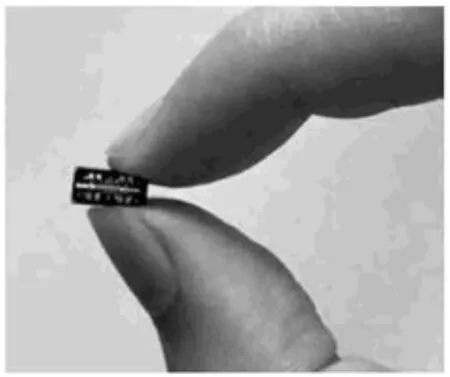
图4 微缩的陀螺元件
基于相同原理,将一个弹性柱体的侧面贴上压电基片,沿x轴方向施加交变激励使柱体产生弯曲振动.在相隔90◦的另一侧面也贴上压电基片,当载体绕z轴转动时,量测科氏惯性力激起的沿y轴的弹性位移以提供角速度信息[3](图5).

图5 柱式振动陀螺
振动陀螺的另一种微缩设计由一个弹性圆环构成[4].实验和理论分析都证明,对圆环沿x轴施加交变的激励力,可出现4个波腹伴随4个节点的拍振动.沿 x轴的波腹 A,A′和沿 y轴的波腹 B,B′处有最大径向相对速度.当载体绕z轴以角速度ω转动时,圆环上各点产生切向的科氏惯性力.在A点至B点的范围内,科氏惯性力的合力FC作用于45◦方向的节点 C.A′点至 B′点范围内的科氏惯性力合力FC′作用于节点C′.圆环受交变的惯性力FC和FC′的驱动,在节点C和C′处产生附加径向振动,其振幅与角速度ω的大小成正比(图6).
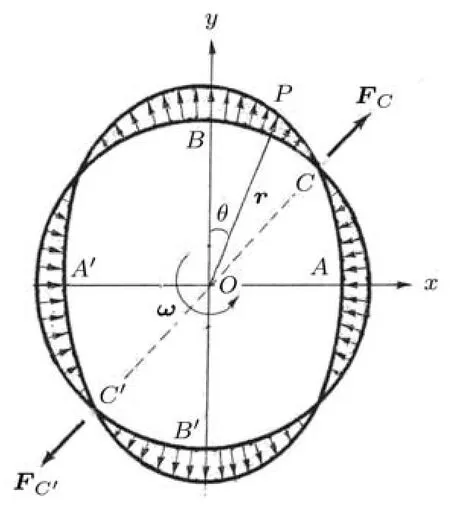
图6 圆环式振动陀螺
上述几种振动陀螺仪均可利用MEMS加工方法制成微型惯性元件,装在手机里量测转动角速度,积分后提供转角信息.利用电阻或电容因压力变化的微型元件还可提供加速度信息.微型振动陀螺仪成本低廉可批量生产,与导航系统的精密陀螺仪相比,精度虽低但能满足民用要求.因此是广泛用于民用产品的惯性元件.不仅用于手机,而且在照相机防抖、虚拟现实的眼镜、自平衡滑板、使用气囊的汽车安全系统等消费领域里,微型陀螺仪也大有用武之地.
附录1 质点式振动陀螺的力学分析
设质量为m的质点与刚度为k沿x轴和y轴的弹簧组成二自由度质量弹簧系统 (图 3).设沿 x轴对质点施加角频率为ν的周期激励F cosνt,基体绕z轴以角速度ω转动,考虑科氏惯性力,列写质点的动力学方程

方程(1)有以下特解
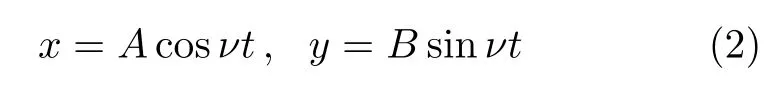
将式(2)代入式(1),因待测的角速度ω远小于激励角频率ν,仅保留ω/ν的一次项,解出
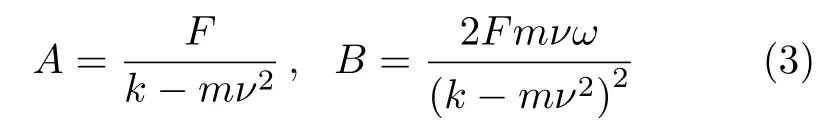
质点沿y轴受迫振动的振幅 B与载体转动角速度ω成正比,可用于提供角速度信息.沿 y轴和沿 x轴的振动之间有90◦相位差.如激励频率ν接近质点单向振动的固有频率则出现谐振现象,A和B均增大使信号增强.
附录2 圆环式振动陀螺的力学分析
如图6所示,设圆环中心线上任意点P相对中心点O的矢径r与y轴的夹角为θ,圆环在力矩作用下的拍振动以θ和t的函数表示为
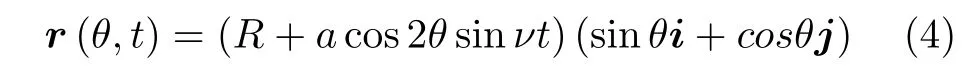

其中R为圆环半径,a,ν为拍振动的振幅和角频率.P点的相对速度v沿径向,以x轴和y轴的基矢量i,j表示为设基体绕z轴以角速度ω转动,圆环的单位长度质量为ρ,P点处长度为ds=Rdθ的微元体上作用沿切向的科氏惯性力

计算科氏惯性力在(x,y)平面第一象限内的合力,得到
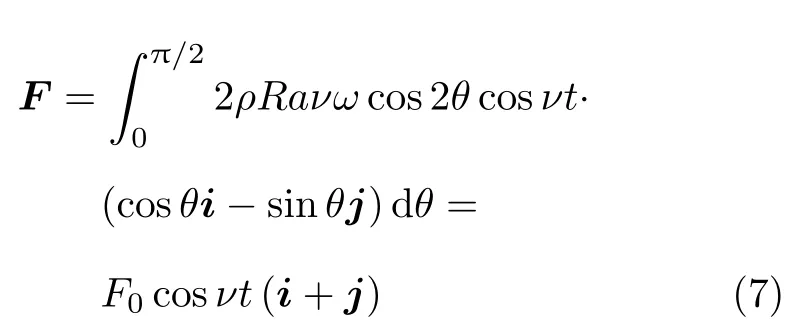
此合力沿θ=45◦方向,幅值F0与角速度幅值ω成正比

科氏惯性力的合力F导致圆环在θ=45◦方向产生附加振动,振幅与角速度ω成正比,与x轴的振动之间有90◦相位差.计算其他象限内的科氏惯性力合力,可得到类似结果.
1 成宇翔,张卫平,陈文元等.MEMS微陀螺仪研究进展.微纳电子技术,2011,48(5):277-285
2 Cetin H,Yaralioglu GG.Analysis of Vibratory Gyroscopes:Drive and Sense Mode Resonance Shift by Coriolis Force.IEEE Sensors Journal,2017,17(2):347-358
3 Ghommem M,Nayfeh AH,Choura S.Model reduction and analysis of a vibrating beam microgyroscope.Journal of Vibration and Control,2012,19(8):1240-1249
4 Yoon SW,Lee S,Najafi K.Vibration sensitivity analysis of MEMS vibratory ring gyroscopes.Sensors and Actuators A:Physical,2011,171(2):163-177
O313
A
10.6052/1000-0879-17-219
本文于2017-06-19收到.
1)刘延柱,教授,E-mail:liuyzhc@163.com
刘延柱,杨晓东.藏在手机里的微型陀螺仪.力学与实践,2017,39(5):506-508
Liu Yanzhu,Yang Xiaodong.Microscale gyroscopes hidden in cellphones.Mechanics in Engineering,2017,39(5):506-508
(责任编辑:周冬冬)

