上倾管道充气排液过程两相流动特性
郭 芮, 张伟明, 姜俊泽, 李 江, 张源涛
(中国人民解放军后勤工程学院军事供油工程系,重庆 401311)
上倾管道充气排液过程两相流动特性
郭 芮, 张伟明, 姜俊泽, 李 江, 张源涛
(中国人民解放军后勤工程学院军事供油工程系,重庆 401311)
在直径为40 mm、倾斜角为20°的管道内,以空气、水为试验介质,利用高速摄影仪和数据采集仪对上倾管道充气排液过程气液两相流动特性进行研究。建立跟随气泡和领先气泡速度比与气泡距离的关系,对比不同入口气体流速下管道内部压力、流量、气泡变化特性。结果表明,充气排液过程分为4个阶段,气体侵入和气液喷发阶段是气液混合物产生阶段,此阶段上倾管内流型以段塞流为主。管道底部压力和出口流量随气体流速的增大而增大,排空时间随气体流速的增大而减小。气体侵入过程气泡呈合并趋势,入口气速越大气泡越长,形状越不规则,领先气泡的速度和液体速度呈线性关系。Hout公式与本文中拟合公式最为接近。
上倾管道; 充气排液; 段塞流; 气液两相流; Taylor气泡
机动输油管线是野战条件下输送油料的装配式管线系统。管道在撤收时需要将管线中的残油排出,以便重复利用。采用压缩空气从管线一端注气排液是目前较为经济、高效的手段。对于水平或下坡管道,液体较易排空,但是当管线遇到上坡段时,充气过程将产生气液两相流,气液混合物以段塞流形式存在[1],气体以Taylor气泡的形式进入液体,液体从管道另一端排出。段塞流的产生使排空过程参数具有一定的复杂性和波动性[2],同时导致排空结束管道中形成大量积液,影响管线的撤收。Lizarraga-Garcia等[3-4]通过数值模拟的方式模拟管道中Taylor气泡的运动规律,得到了统一的Taylor气泡上升速度公式。Behafarid等[5]研究了管道中长距离可变形气泡动力特性及气泡间液层、管壁弯头对段塞流动的影响。姜俊泽等[6]采用VOF模型对管道充气排液工况进行了数值模拟,研究分析了充气过程中不同时刻的管道内压力分布、气相体积分数、管流摩阻和能量交换情况,得到这一工况下气液两相的流动特性。Callie等[7]研究了垂直和倾斜管中气泡在牛顿和非牛顿流体中的上升速度,发现气泡上升过程的弗鲁德数与管长、倾角和流体物性参数均有关系。关于管道段塞流的形成和发展已经有了一些研究[8],但是气泡产生方式多为常压释放或冷凝释放[9],鲜有采用压缩气体侵入常规液体管道的研究,而机动管线排空过程需要采用空压机释放较大压力的压缩空气将液体排出,有必要研究这一特定工况下的两相流动特性。笔者以空气、水为工质,利用高速摄影仪和数据采集装置对上倾管道充气排液过程两相流动特性进行研究。
1 试 验
1.1 设 备
上倾管道充气排液试验装置如图1所示。整个试验装置由注水系统和排空系统组成。注水系统的作用是在排空之前将管路注满水,由离心泵、水箱、阀门组成。排空系统由压缩机、缓冲罐、气体流量计、有机玻璃管、液体流量计组成。
试验采用活塞式空压机,型号为SUB50-15/40(额定排气量18 m3/h,排气压力0.1 MPa),空压机出口安装气体缓冲罐,以保证管道入口气体流量稳定。气体垂直注入管道,装配图如图2所示。管路系统由微下倾管、弯头和上倾管组成。下倾、上倾管采用有机玻璃管,弯头采用钢丝橡胶管。微下倾管设置的目的是保证气液混合物在进入上倾管之前处于分层流动,避免对上倾管段塞流的干扰。上倾管路倾角为20°,管长为2 m,内径为40 mm。为获取出口液体流量,在上倾管出口安装KATflow200型超声流量计(量程为0.01 ~25 m/s,精度等级0.5级)。空压机出口、上倾管底和上倾管顶分别安装MIK-P300型号压力传感器(量程范围为-0.1 ~ 0.1 MPa,精度等级0.1级)。为捕捉管路中Taylor气泡的清晰图像,在上倾管中间位置距离管道1 m处安装高速摄影仪。采用Photron公司FASTCAM Ultima512型高速摄影仪,采集速度为500帧/s。
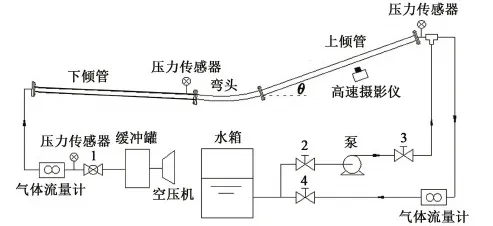
图1 试验流程Fig.1 Experimental flow loop
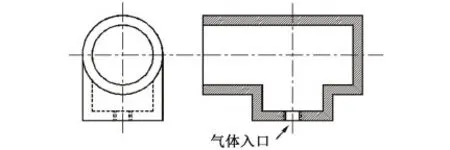
图2 注气装置Fig.2 Configuration of gas injector
1.2 试验步骤
试验在室温17°C下进行,首先打开阀门2、3,关闭阀门1、4,开启离心泵向管路中注水,通过观察玻璃管中水量判断是否注满。然后关闭阀门2、3,开启阀门1、4,开启空压机,通过改变空压机出口阀门1的开度来控制气体流速,流速变化范围UG=0 ~ 1.32 m/s。利用高速摄影仪记录上倾管内Taylor气泡流动过程,排空结束后关闭空压机,打开弯头将残液卸流,进行下一组试验。
1.3 误差分析
试验的误差主要源于测试仪表,采用测量不确定度来表示实测数据的误差范围。测量的物理量有压力和流量,其中压力为间接测量参数,流量为直接测量参数。压力传感器精度等级0.1级,输出标准两线制电流信号经250 Ω标准电阻转换为1~5 V电压信号,通过研华公司USB4711A数据采集模块读入计算机,采集卡的模/数转换精度等级为0.012级,则测量电压时的最大偏差为δU=0.1%×5 V+0.012%×5 V=0.005 6 V。则压力的不确定度为δP=0.05δU=0.28 kPa。压力的相对不确定度为δP/δPmin=4.6%。
液体流量通过KATflow200型超声流量计测量,精度等级为0.15。流量计直接输出数字信号,因此不存在转换误差,仪表提供的精确度为所测流量的相对不确定度,即0.15%。
2 试验结果及其讨论
2.1 排空全过程压力流量变化规律
不同入口气速下上倾管底压力p与出口液体流量Q随时间的变化关系示于图3。排空过程管内流态变化可以分为4个阶段:①液体流出;②气体侵入;③液气喷发(mixture production);④液塞震荡(slug oscillation),如图4所示。首先,打开阀门1的瞬间,由于管内静压较大,管线入口出现瞬时憋压,出口压力跃升。出口压力稳定后,排空正式开始,上倾管底部压力开始稳定上升,原因是此阶段液体做加速运动,速度越来越快,测压点之后的压降越来越大,因此此点压力缓慢上升。气体进入上倾管时,排空第二阶段开始,上倾管内出现气液混合物。此时压力出现陡降,原因是由于气体的置换作用,上倾管内静水压力减少,为平衡减小的静水压力,上倾管底部压力相应减小。前两阶段液体流量基本不变,因为排气压力较小,液体可以看作准稳态流动。随着气液混合物中的领先气泡到达管顶,气液混合物开始被排出,排空进入第三阶段即气液喷发阶段。由于此阶段大部分液体已被排出,管内残余液体以间歇段塞的形式震动,所以底部压力不再减小,而是以不稳定周期进行波动。此阶段流体以段塞流的形式间断排出,排出的瞬间液体流量迅速增长。气液喷发结束后,管内残余液体较少,剩余液体无法形成完整大段塞,气体流速不足以将液体携带出管道,因此液体以小段塞的形式在管内循环震荡。管底压力继续波动,出口流量为零。

图3 压力和流量随时间变化关系Fig.3 Measured pressure and flow rate variation with time changing
由于大部分液体在前两个阶段被排出,而且第三阶段混合物喷发过程排液量较少且具有一定的随机性,因此前两阶段为排空阶段,对应的时间为排空时间。由图3可得,4种工况下排空时间分别是15.6、11.1、8.6和8.5s,最大流量分别为2.59、2.77、3.13和4.03 m3/h,即随着气速增加,排空时间减小,排空速度增大。
2.2 排水期Taylor气泡变化规律
2.2.1 气泡外形变化
本试验条件下,气液喷发阶段仅观察到了段塞流一种流型。段塞流每个液塞单元中间的弹状气泡被称为Taylor气泡[10]。图5为入口气速为0.88 m/s工况下上倾管内Taylor气泡演变过程。观测段为整个上倾管,起始点分别距离空压机出口57D和107D(D为管径)。Taylor气泡在排空过程中分为产生、增长和合并3个阶段。气泡从入口处产生,逐渐与前面的气泡合并,领先的气泡不断增长,在管顶达到最大值,这与Liu等[11]的研究结论类似。t=10 s时气体进入上倾管,Taylor气泡形成,随后领先气泡不断被跟随气泡合并,合并细节如图5(t=11.41~11.59 s)所示。在领先气泡和若干跟随气泡流出管道后,气液喷发过程结束,剩余残留液体因无法被排出而在管内震荡,呈循环段塞的形式,图5中t=26.21~26.77 s显示了循环段塞从产生、增长到溃灭的一个完整周期。

图4 流动状态示意图Fig.4 Stages of evacuation process
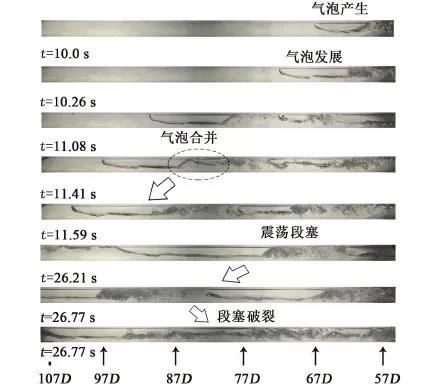
图5 入口气速0.88 m/s时气泡随时间演变示意图Fig.5 Taylor bubble evolution for UG=0.88 m/s
图6为不同气速下同一观测段领先气泡到达管路出口,即气液喷发阶段开始瞬间的气泡形状。对比3种工况下领先气泡的长度,可知,气速越大,气泡长度越大。对比领先气泡的形状,当气速较低时(UG=0.44 m/s),领先气泡能够保持结构的完整性,分为气鼻、气泡主体和气尾。气泡尾部有清晰的水跃(hydraulic jump),受重力和惯性力控制。气速较高时(UG=0.88,1.10 m/s),气泡尾部湍流强度较大,形成不规则湍流涡旋(turbulent eddies)。气体流速越大,气泡之间的液弹中夹带的小气泡数量越多,原因是液体速度越快,气泡稳定性越低,气泡尾部的小气泡越容易脱离。对比3种工况下的气泡数量,气体流速越大,上倾管内气泡数量越少,原因是随着气速增加,气泡合并速度更快,气液喷发瞬间,大量小气泡已并入了领先气泡。
2.2.2 Taylor气泡速度变化规律
由于受到试验管道长度限制,气顶排液过程持续时间较短,跟随气泡不断地被领先气泡合并,领先气泡的长度呈规律性增长,气泡并未得到充分发展。在此只讨论领先气泡的速度变化规律。

图6 不同气速上倾管内Taylor气泡形态对比Fig.6 Taylor bubble shape in ascending pipe for different gas velocity
经试验观察,排液过程中领先气泡近似匀速运动,因此只讨论排空过程中的平均速度。领先气泡平均速度ULTB的大小可以由气泡在前后两个不同时刻的相对位置决定,如图7所示。气泡在n1和n2两帧之间运动的平均速度可由两个时刻的相对位置确定。

图7 气泡速度测量方法Fig.7 Bubble velocity measurement
速度计算式为

(1)
式中,x1、x2分别为n1帧和n2帧气泡头部对应在侧面标尺上的坐标;fps为相机采集频率;γ为标度因子,即标尺中每一单位长度对应的实际长度。
管道真实长度已知,因此其计算方法为γ为两点间真实距离/两点在标尺上的距离。
关于段塞流气泡上升规律的研究主要针对常压下向静止液体释放气泡[12]或气液混输工况[13-14],研究发现段塞流中气泡流动速度UTB和气液两相折算速度近似呈线性关系,表达式为
UTB=C0Um+Ud.
(2)
式中,Um为气液混合物折算速度,即气相和液相的速度之和;Ud为静水中Taylor气泡漂移速度;C0为无量纲分布参数,仅与液体速度有关。
本试验为单相压缩气体注入静止液体,入口不存在气液混合物,探讨领先气泡和出口液体速度之间的关系。排液过程近似看作准稳态流动,管道出口仅为液体,因此取液体速度的平均值为计算对象。液体平均速度计算方法为在液体流出阶段将流量取平均值。每个工况下液体平均速度和领先气泡平均速度如表1所示。将试验数据进行线性回归,得到领先气泡和液体速度的关系曲线为ULTB=1.639 92UW+0.150 68,如图8所示。
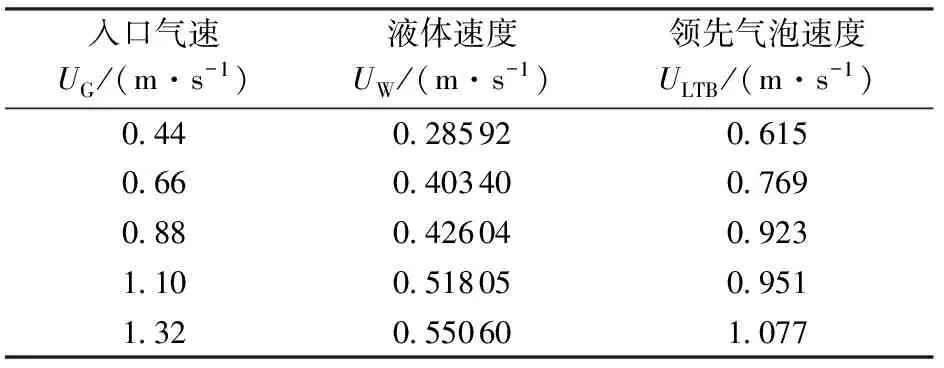
表1 速度变化
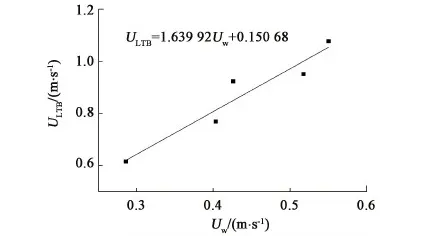
图8 气泡速度拟合Fig.8 Bubble velocity fitting
2.2.3 Taylor气泡合并规律
选取3种工况对领先气泡和追随气泡的合并进行研究。从气泡产生开始,记录前两个气泡的间距和瞬时速度变化,计算出每一个间距下的速度比值,如图9所示。根据Mayor等[15]的研究,采用指数函数对其进行拟合,拟合关系式为
(3)
式中,ULTB为领先气泡速度;UTTB为跟随气泡速度;a、b、c、d的取值见表2。
图9为速度比值和气泡间距关系的拟合曲线。Hout等[16]指出,领先的Taylor气泡尾部流场会对其后的气泡产生扰动,导致跟随气泡速度大于领先气泡,这种扰动可以波及至领先气泡尾部50D范围内,所以跟随气泡和领先气泡的速度比始终大于1。Liu等[11]发现当Taylor气泡间距小于2.5D时合并趋势较强烈。由图9可得气泡间距大于4D时,气泡速度相对恒定,没有很强的合并趋势,但是当间距小于4D时,速度比陡增,气泡呈现很强的合并趋势。与Liu等的研究结果不同的原因是本文管径较大,表面张力作用较小,气泡稳定性较弱,所以同一间距下的合并趋势更加强烈。
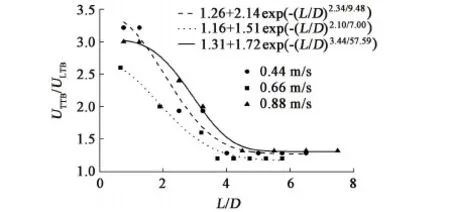
图9 三种工况下气泡合并速度比值和气泡间距的关系Fig.9 Velocity ratio of trailing Taylor bubble to leading one as a function of bubble distance under three conditions
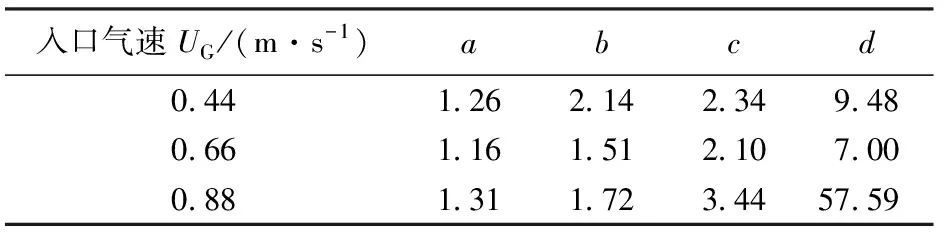
入口气速UG/(m·s-1)abcd0441262142349480661161512107000881311723445759
图10为气速0.66 m/s工况下的拟合曲线同Moissis & Griffith[17]、Hout等[18]和Mayor等[19]的公式的对比图。
由图10可得,Hout公式与本文试验最为接近。原因是本文将压缩空气注入静止液体,产生连续的Taylor气泡,领先气泡的前方无任何干扰,其速度不变,所以气泡速度比仅取决于跟随气泡的速度。而Moissis和Mayor等的研究均为气液混输工况,研究对象为持续段塞流中某一个中间气泡及其跟随气泡的速度,因此领先气泡前端均存在加速现象。Hout公式虽为连续气泡下的工况,但是参考了Nicklin等[20]给出的流动液相中的Taylor气泡速度,将领先气泡的速度取为定值,避免了领先气泡速度波动对结果的影响,因此与本文中公式较为接近。
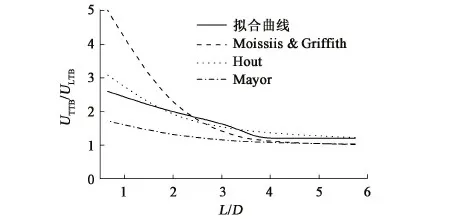
图10 排空过程Taylor气泡相互作用曲线和已有研究对比Fig.10 Taylor bubble interaction curves with previous studies
3 结 论
(1)排空过程可分为液体流出、气体侵入、液气喷发、液塞震荡4个阶段,其中气体侵入阶段上倾管内流型为段塞流。
(2)入口气体流速对排空时间、上倾管底压力、出口流量有显著影响。入口流速越大,液体流量也越大,排空时间越短,压力波动幅度越大。
(3)排空过程上倾管内气泡呈现合并的趋势,入口流速越大领先气泡越长,形状越不规则。气泡速度和液体流速呈线性变化关系。Hout公式与本文中拟合公式最为接近。
[1] MOREIRAS J, PEREYRA E, SARICA C, et al. Unified drift velocity closure relationship for large bubbles rising in stagnant viscous fluids in pipes[J]. Journal of Petroleum Science & Engineering, 2014,124:359-366.
[2] LI N, GUO L, LI W. Gas-liquid two-phase flow patterns in a pipeline-riser system with an S-shaped riser[J]. International Journal of Multiphase Flow, 2013,55:1-10.
[3] LIZARRAGA G E, BUONGIORNO J, Al-SAFRAN E,et al. A broadly-applicable unified closure relation for Taylor bubble rise velocity in pipes with stagnant liquid[J]. International Journal of Multiphase Flow, 2017,89:345-358.
[4] LIZARRAGA G E, BUONGIORNO J, BUCCI M. An analytical film drainage model and breakup criterion for Taylor bubbles in slug flow in inclined round pipes[J]. International Journal of Multiphase Flow, 2016,84:46-53.
[5] BEHAFARID F, JANSEN K E, PODOWSKI M Z. A study on large bubble motion and liquid film in vertical pipes and inclined narrow channels[J]. International Journal of Multiphase Flow, 2015,75:288-299.
[6] 姜俊泽,张伟明,李正阳.管道充气排液工况下气液两相流数值模拟研究[J].系统仿真学报,2013,25(2):383-388.
JIANG Junze, ZHANG Weiming, LI Zhengyang. Mathematic simulation on gas-liquid two-phase flow of pipe pigging by gas condition[J]. Journal of System Simulation, 2013,25(2):383-388.
[7] CALLIE E S, RYAN M E. An experimental study of the motion of long bubbles in inclined tubes[J]. Chemical Engineering Science, 2001,56(6):2191-2204.
[8] 杨娅君,刘楚芸,段毅,等.漂移流模型用于毛细管两相流数值计算[J].高校化学工程学报,2004,18(3):303-307.
YANG Yajun, LIU Chuyun, DUAN Yi, et al. A drift flux model for numerical simulation of two-phase refrigerant flow through capillary tubes[J]. Journal of Chemical Engineering of Chinese Universities, 2004,18(3):303-307.
[9] LIU Y P, WANG P Y, WANG J,et al. Investigation of Taylor bubble wake structure in liquid nitrogen by PIV technique[J]. Cryogenics, 2013,55/56(5):20-29.
[10] AZEVEDO M, SANTOS D, FACCINI J, et al. Experimental study of the falling film of liquid around a Taylor bubble[J]. International Journal of Multiphase Flow, 2016,88:133-141.
[11] LIU Y, WANG P, HU X,et al. Visualization research on characteristics of the cryogenic slug flow in vertical and inclined tubes[J]. Canadian Journal of Chemical Engineering, 2015,90(6):1588-1601.
[12] IRIKURA M, MAEKAWA M, HOSOKAWA S,et al. Numerical simulation of slugging of stagnant liquid at a V-shaped elbow in a pipeline[J]. Applied Mathematical Modeling, 2014,38(17/18):4238-4248.
[13] Al-SAFRAN E, SARICA C, ZHANG H Q,et al. Investigation of slug flow characteristics in the valley of a hilly-terrain pipeline[J]. International Journal of Multiphase Flow, 2005,31(3):337-357.
[14] ROITBERG E, BARNEA D, SHEMER L. Elongated bubble shape in inclined air-water slug flow[J]. International Journal of Multiphase Flow, 2016,85:76-85.
[15] MAYOR T S, PINTO A M F R, CAMPOS J B L M. Hydrodynamics of gas-liquid slug flow along vertical pipes in turbulent regime: a simulation study[J].International Journal of Heat & Fluid Flow, 2007,85(11):1497-1513.
[16] HOUT R V, SHEMER L, BARNEA D. Evolution of hydrodynamic and statistical parameters of gas-liquid slug flow along inclined pipes[J]. Chemical Engineering Science, 2003,58(1):115-133.
[17] MOISSIS R, GRIFFITH P. Entrance effects in a two-phase slug flow[J]. Journal of Heat Transfer, 1962,84(1):29-38.
[18] HOUT R V, BARNEA D, SHEMER L. Evolution of statistical parameters of gas-liquid slug flow along vertical pipes[J]. International Journal of Multiphase Flow, 2001,27(9):1579-1602.
[19] MAYOR T S, PINTO A M F R, CAMPOS J B L M. Hydrodynamics of gas-liquid slug flow along vertical pipes in the laminar regime: experimental and simulation study[J]. Industrial & Engineering Chemistry Research, 2007,46(11):3794-3809.
[20] NICKLIN D J, WILKES J O, DAVIDSON J F. Two-phase flow in vertical tubes[J]. Transactions of the Institute of Chemical Engineers, 1962,40:61-68.
(编辑 沈玉英)
Gas-liquidflowcharacteristicsinevacuationprocessforascendingpipelines
GUO Rui, ZHANG Weiming, JIANG Junze, LI Jiang, ZHANG Yuantao
(DepartmentofMilitaryPetroleumSupportingEngineering,LogisticalEngineeringUniversity,Chongqing401311,China)
An experiment investigation was conducted in a pipeline with the radius 40 mm and the ascending angle 20°, where the gas and water are used as the mediums. The high speed camera and data collector are utilized to study the gas-liquid two phase flow characteristics in the liquid draining process. The function of the velocity ratio between the leading bubble and following bubble, with respect to the bubble distance was established. Then the internal pressure, the flow and bubble variation characteristics were compared for different inlet velocities. The results show that the liquid evacuation process is divided into four stages, where the gas invasion and gas-liquid eruption stage deals with the production of the mixture of gas and liquid, and the slug flow is the main flow type in the ascending pipeline. The bottom pressure and outlet flow rate increase, while the draining time decreases with the increase of the inlet velocity. The leading bubble takes on a merging and increasing tendency. The bubble becomes longer and less regular with the increase of the inlet velocity. The velocity of the leading bubble is linearly related with the outlet velocity. Also it is found that the Hout formula is close to the fitted one in the current work.
ascending pipeline; liquid evacuation; slug flow; gas-liquid two phase flow; Taylor bubble
2017-02-22
后勤工程学院研究生创新基金项目 (20151230);重庆市博士后特别资助项目(xm2016026)
郭芮(1989-),男,博士研究生,研究方向为油气输送技术与装备。E-mail:934425166@qq.com。
1673-5005(2017)05-0146-07
10.3969/j.issn.1673-5005.2017.05.018
TP 391.9
A
郭芮,张伟明,姜俊泽,等.上倾管道充气排液过程两相流动特性[J]. 中国石油大学学报(自然科学版), 2017,41(5):146-152.
GUO Rui, ZHANG Weiming, JIANG Junze, et al. Gas-liquid flow characteristics in evacuation process for ascending pipelines [J]. Journal of China University of Petroleum (Edition of Natural Science), 2017,41(5):146-152.

