随钻方位电磁波测井仪器偏心响应模拟及分析

巫振观, 范宜仁, 王 磊, 刘家雄, 邢 涛

(1.中国石油大学地球科学与技术学院,山东青岛 266580; 2.中国石油大学CNPC测井重点实验室,山东青岛 266580)

随钻方位电磁波测井仪器偏心响应模拟及分析

巫振观1,2, 范宜仁1,2, 王 磊1,2, 刘家雄1,2, 邢 涛1,2

(1.中国石油大学地球科学与技术学院,山东青岛 266580; 2.中国石油大学CNPC测井重点实验室,山东青岛 266580)

为研究随钻方位电磁波测井仪器偏心响应特征,基于交错网格时域有限差分方法,进行复杂偏心条件下测井响应模拟分析。采用共形网格技术实现复杂边界电导率等效,并通过与半解析解对比,验证算法正确性;进而对比分析仪器居中和偏心条件下电磁场分布特征;讨论不同仪器参数及井眼环境下单发单收结构的测量信号变化规律;最后探讨复杂偏心条件下随钻方位电磁波测井响应特征及方位信号变化。结果表明:油基钻井液和电阻率大于0.5 Ω·m的水基钻井液中随钻方位电磁波响应基本不受仪器偏心的影响;电阻率小于0.1 Ω·m的水基钻井液中,低频长源距测量模式可忽略偏心影响,能够较好地用于地质导向;而高频短源距测量模式受井眼环境影响严重,应当考虑适当的校正。

随钻方位电磁波测井; 仪器偏心; 三维时域有限差分; 共形网格

实时地层界面探测及地层电阻率确定是大斜度井/水平井钻井地质导向及储层评价的关键,随钻电磁波测井因其较大的探测深度、对地层界面敏感、能准确提供地层电阻率信息等优点得以广泛应用。近年来不断推广的随钻方位电磁波测井仪器,则通过引入倾斜线圈、正交线圈设计[1-2],弥补了传统随钻电磁波测井缺乏方位敏感性的不足,使得实时地质导向和地层评价更加精确。国内外学者针对随钻方位电磁波测井响应及应用开展了大量研究,揭示了其在大斜度井/水平井中的响应规律[3],讨论了方位信号的影响因素[4],并对实测数据进行了分析[5],在地质导向和地层评价中取得了较好的效果。大斜度井/水平井随钻测量中,受钻井仪器振动及重力作用影响,仪器将偏离井轴,这可能导致基于测井数据的地层边界和电阻率确定出现偏差[6]。为此,Hue和Teixeira等[7]建立了仪器偏心模型,模拟了传统随钻电磁波测井在偏心条件下的响应特征;魏宝君等[6,8]进一步分析了钻井液类型、地层电阻率以及仪器参数等对偏心响应的影响;Lee等[9-10]则考察了偏心条件下各向异性地层响应特征,并探索分析了倾斜线圈系响应规律,提高了随钻电磁波测井地质导向和地层评价的效果和精度。但是,国内外对于随钻方位电磁波测井仪器偏心的系统研究仍然较少,对偏心条件下测井响应的认识亟待完善。笔者基于交错网格三维时域有限差分法,采用共形网格技术进行复杂边界网格电导率等效,讨论仪器偏心条件下单发单收结构电磁波测井响应规律,并进一步以Schlumberger公司的PeriScope仪器为例,系统分析随钻方位电磁波响应特征,研究偏心条件下方位信号的影响因素,为基于随钻方位电磁波测井的地质导向和储层评价提供理论指导和技术支持。

1 电磁波测井时域有限差分方法

1.1 模型建立

大斜度井/水平井中,受重力作用及钻铤振动等的影响,随钻测井仪器将偏离井轴,出现仪器偏心的情况。为此,建立图1所示偏心模型,图1(a)中Rt为地层电阻率,Rmud为钻井液电阻率,发射线圈到接收线圈中点的距离为源距,对于单发单收的双线圈系结构,源距为发射与接收线圈的距离;图1(b)中,定义θR为接收线圈倾角,反映线圈倾斜程度,βR为仪器旋转的方位角;图1(c)中rb为井眼半径,rc为线圈在水平方向上投影的半径,rm为钻铤半径,roffset为仪器偏心距,βE为仪器偏心方位。

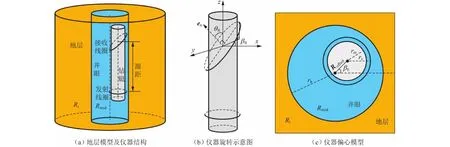
图1 随钻方位电磁波仪器偏心模型示意图Fig.1 Schematic diagram of azimuthal LWD and eccentric borehole model

1.2 柱坐标系下差分格式

考虑井眼及测井仪器的柱状结构,为减小网格与模型不匹配造成的误差,本文中采用圆柱坐标系时域有限差分方法进行三维随钻方位电磁波测井数值模拟。电磁波测井中,源位于发射线圈,从而井眼及地层中满足无源区Maxwell旋度方程,在圆柱坐标系下写成分量形式:

(1)

式中,H和E分别为磁场和电场,下标表示不同方向分量;ε为地层介电常数;μ为地层磁导率;σ为地层电导率;σm为地层导磁率。

基于交错网格时域有限差分方法,对式(1)进行离散,获得电场和磁场的推进公式,此处以周向分量为例:

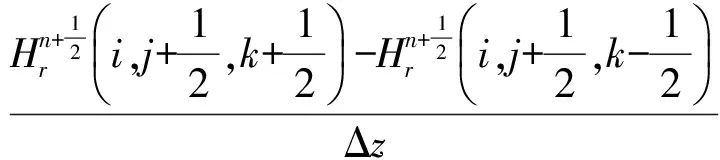
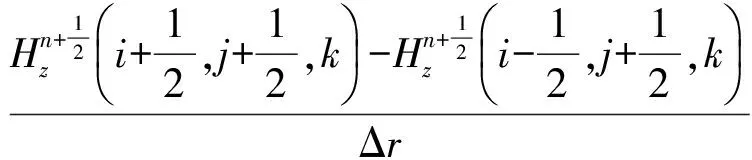
(2)

其中

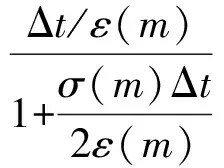
式中,i,j,k为节点空间坐标;n为时间节点。

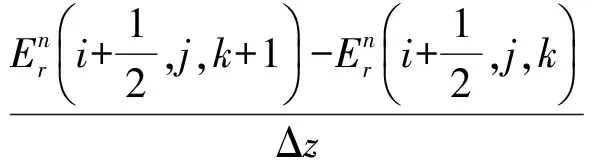
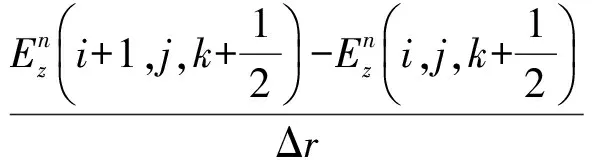
(3)

其中

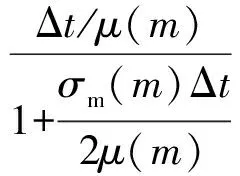
由式(2)可以看出,当前时刻周向上的电场可由上一时刻周向上电场和前1/2时刻径向和纵向磁场计算得到;磁场类似,从而实现电场和磁场的交替推进。

1.3 仪器偏心与倾斜线圈处理

存在仪器偏心时,仪器与井眼、地层的几何关系更为复杂,导致地层模型的精确剖分与刻画更为困难。细化网格剖分可以有效减小模型与网格不匹配造成的误差,但是,随着网格的加密,计算时间成本及内存要求将大大增加。为了更加高效、精确地研究复杂井眼条件下的仪器偏心响应,采用局部共形网格技术,以减小阶梯近似误差。

图2(a)所示,Ot为仪器轴心,Ob为井轴心,A1～An为井眼边界与纵向网格交点,B1～Bm为井眼边界与周向网格交点。可见,剖分网格与模型无法完全匹配时,与模型边界相交的网格内同时包含两种介质,可以根据边界两侧介质所占棱的比例,确定网格的等效参数[7],图2(c)所示,以径向等效电导率确定为例:

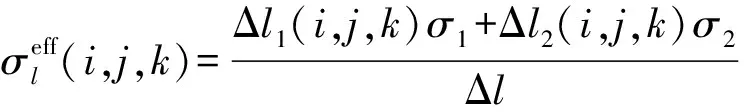
(4)

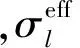
接收线圈感应电动势可由电场沿线圈积分求得,如下式:

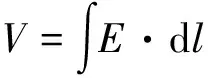
(5)

式中,E为接收线圈所在处沿线圈方向的电场;dl为沿接收线圈方向的微元。将式(5)分解为周向分量和纵向分量求解,如下式:

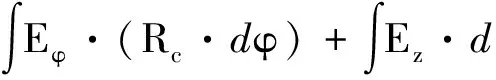
(6)

式中,Eφ为线圈所在处周向电场分量;Ez为纵向电场分量;Rc为线圈半径;dφ为周向网格步长。

由式(6)可知,接收线圈感应电动势可分解为周向和纵向求取,图2(b)所示C1C2C3C4组成的网格中,N1和N2为倾斜线圈与网格交点,则线圈处周向电场分量可通过上下周向棱上的电场插值得到;纵向分量电场计算时,则通过左右棱上纵向电场分量插值获取。

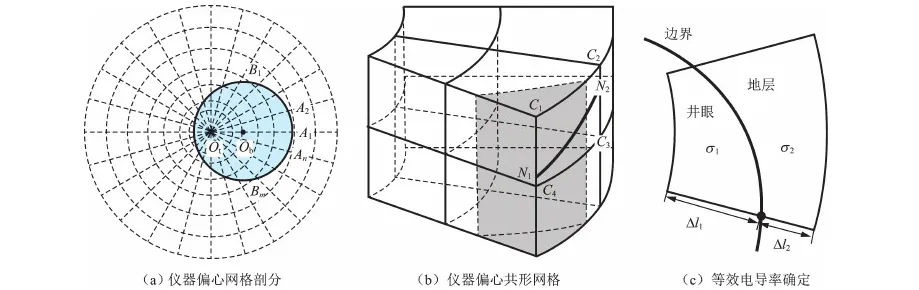
图2 仪器偏心及共形网格示意图Fig.2 Schematic diagram of eccentric and conformal grid

1.4 模型验证

通过同一地层模型条件下三维时域有限差分与半解析解法所得模拟结果对比,分别验证倾斜线圈和偏心程序的正确性。设定无限厚均匀地层,且其电阻率10 Ω·m,忽略井眼;仪器频率2 MHz,源距[60.96 76.2] cm,发射线圈倾角为0°,计算不同接收线圈倾角下相位差和幅度比。图3为本文中三维时域限差分方法与文献[10]半解析解的对比结果,可以看出,两者的计算结果很好地吻合。

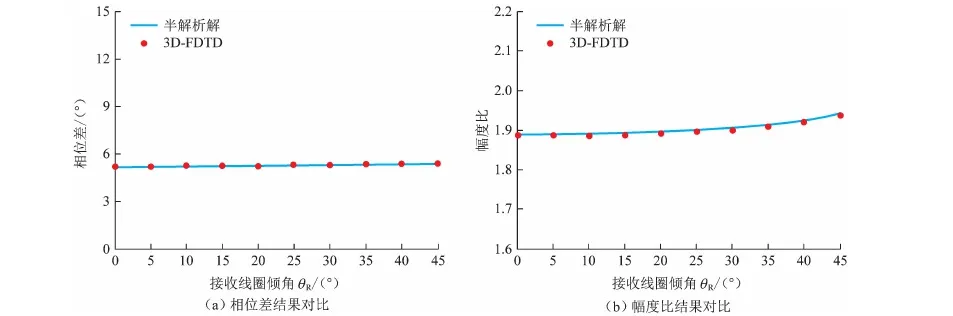
图3 倾斜线圈程序验证Fig.3 Validation of tilted coil codes

对于传统随钻电磁波测井,仪器发射线圈和接收线圈为同轴设计。设地层均匀且电阻率为0.1 Ω·m,井内钻井液电阻率2 000 Ω·m,井眼半径30.48 cm,仪器发射频率为2 MHz,线圈距为[60.96 76.20] cm,计算不同仪器偏心距时接收线圈感应电动势相位差和幅度比。图4为本文中三维时域有限差分方法与文献[7]半解析解对比结果,可以看出,两者的计算结果吻合。

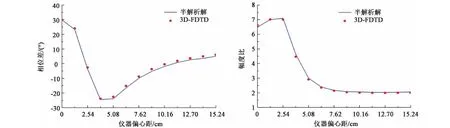
图4 仪器偏心程序验证Fig.4 Validation of eccentric borehole codes

2 偏心条件下线圈系响应特征

单发单收是感应/电磁波类测井最基本的仪器结构,其响应特征直接反映了电磁波测井的探测特性。讨论单一发射线圈在仪器居中和偏心时产生的电磁场,分析仪器参数、井眼环境等对单发单收结构在偏心条件下接收信号的影响,从而更深入地了解仪器偏心时的电磁波测井响应特征。

2.1 电磁场分布

仪器偏心条件下,地层不再关于仪器轴对称,与仪器居中时相比,地层中的电磁场分布将会发生变化。设地层电阻率为10 Ω·m、钻井液电阻率为0.1 Ω·m,井眼半径为30.48 cm,仪器频率为2 MHz,分别对仪器居中和偏心(偏心距15.24 cm)两种情况进行模拟,得到周向电场分布如图5。不难看出,仪器居中时,电磁场的分布关于井轴对称;仪器偏离井轴时,电磁场分布将发生变化,不再关于井轴对称,这势必会改变电磁波测井仪器的测量信号,进而影响方位电磁波测井地质导向和储层评价精度。

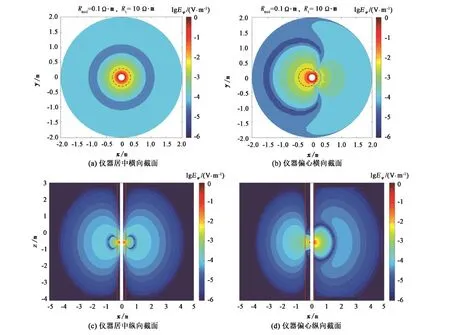
图5 周向电场分量Fig.5 Circumferential electric field distribution

2.2 发射频率及线圈距影响

发射频率和线圈距是电磁波测井仪器的两个重要参数,为了考察仪器偏心对不同发射频率以及不同线圈距下接收线圈处测量信号的影响,分别模拟了高频和低频条件下不同线圈距时仪器偏心响应。设井眼半径为30.48 cm,钻井液电阻率为0.1 Ω·m,地层电阻率为10 Ω·m;高频(2 MHz)和低频(400 kHz)条件下,不同线圈距偏心响应如图6。

模拟结果显示,线圈距不同时感应电动势相位和幅度均不同,线圈距越小,相位和幅度越大;随着仪器偏心距的增大,相位明显增大,幅度变化较小;总体上看,不同线圈距受仪器偏心影响差别不大;仪器发射频率为400 kHz时,相位和幅度受仪器偏心的影响大为减小。

2.3 线圈倾角影响

与传统随钻电磁波仪器相比,随钻方位电磁波测井仪器加入了倾斜线圈,为此讨论线圈不同倾斜程度时响应受仪器偏心影响。设仪器频率2 MHz,线圈距[55.88 71.12] cm,偏心距为0、5.08、10.16、15.24 cm,计算不同接收线圈倾角下响应如图7。可以看出,随着线圈倾角的增大,相位和幅度都增大,表明倾斜线圈的相位和幅度不同于水平线圈。

图6 不同线圈距电磁波响应Fig.6 Response of electromagnetic logging with different coil spacing

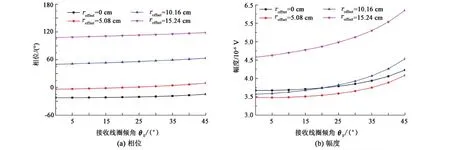
图7 不同线圈倾角下电磁波测井响应Fig.7 Response of electromagnetic logging with different coil inclination

进一步考察仪器偏心对不同倾角线圈的影响,设地层电阻率10 Ω·m,钻井液电阻率0.1 Ω·m,井眼半径30.48 cm,仪器频率2 MHz,线圈距55.88 cm。图8为不同接收线圈倾角条件下,相位和幅度随仪器偏心距的变化。相位随偏心距增大而增大,幅度随偏心距呈非线性变化;仪器偏心距较小时,不同倾角线圈的响应受偏心影响差别较小,随着偏心距的增大,不同线圈倾角仪器受偏心影响的程度也不断增大,且线圈倾角越大,受偏心影响越大。

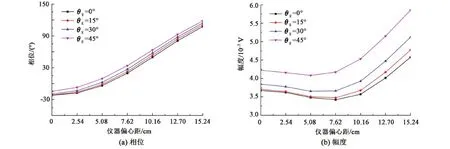
图8 不同线圈倾角下响应随偏心距的变化 Fig.8 Response variation with eccentricity for different coil inclination

2.4 线圈方位影响

仪器居中时,地层中的场具有轴对称性(图5),此时,无论仪器是否旋转,对接收线圈上的信号没有影响,但是仪器偏心条件下,地层中的场不再对称,仪器方位角变化时,接收线圈上的感应电动势也将发生变化。设地层电阻率为10 Ω·m,钻井液电阻率为0.1 Ω·m,井眼半径为30.48 cm,仪器发射频率为2 MHz,线圈距为55.88 cm,仪器偏心距为10.16 cm和15.24 cm。图9所示,仪器旋转至不同方位时,感应电动势相位和幅度不同,相位和幅度随方位角变化曲线关于方位角180°对称。

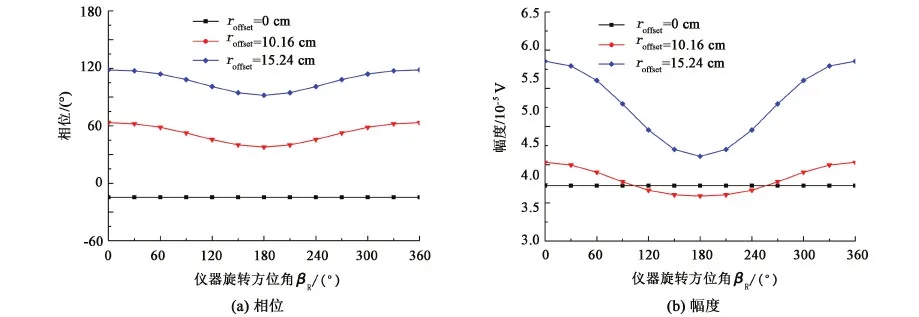
图9 不同方位角下电磁波测井响应Fig.9 Response of electromagnetic logging with different azimuthal angles

2.5 井眼尺寸影响

受地层岩性、应力等的影响,钻井过程中可能出现井眼垮塌、扩径以及缩径等现象,为此,分别模拟不同井径时仪器居中和贴井壁测井响应。图1所示模型,仪器居中时,偏心距为0 cm;仪器贴井壁时,仪器方位角为0°,线圈与井壁距离设为1.27 cm。

设地层电阻率为10 Ω·m,钻井液电阻率为0.1 Ω·m,井眼半径为30.48 cm;仪器发射频率为2 MHz,线圈距为55.88 cm,图10所示为不同线圈倾角条件下两种模型响应随井眼半径变化。仪器居中时,相位和幅度受井眼尺寸影响大,尤其是相位随着井眼半径增大迅速减小。

3 随钻方位电磁波响应偏心分析

3.1 电磁波测井信号合成

电磁波测井中,可提取接收线圈处感应电动势相位差[11]和幅度比[7,12]:

Dp=θR2-θR1,

(7)

(8)

式中,θR1、θR2分别为两个接收线圈处感应电动势的相位;AR1、AR2分别为两个接收线圈处感应电动势的幅度;Dp为相位差;Ra为幅度比。

线圈倾斜时,可根据仪器旋转至不同方位的测量结果提取方位信号,相位方位信号和幅度方位信号可通过相差180°方位的相位和幅度计算得到[14],计算公式如下:

(9)

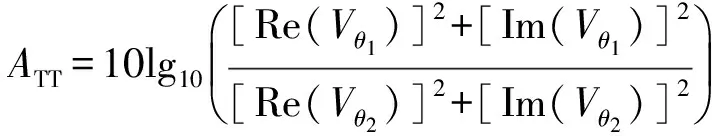
(10)

式中,Im和Re分别表示取变量的虚部和实部;Sp为相位方位信号;ATT为幅度方位信号;θ1和θ2为相差180°的方位角,特别地,取θ1=0°,θ2=180°;Vθ1和Vθ2分别为方位角θ1和θ2时接收线圈的感应电动势。

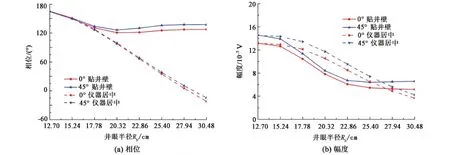
图10 不同井眼尺寸下电磁波测井响应Fig.10 Response of electromagnetic logging with different borehole sizes

3.2 随钻方位电磁波测井响应

设井眼半径30.48 cm,线圈距[55.88 71.12] cm,模拟传统随钻电磁波测井响应随偏心距变化(图11),随钻方位电磁波测井(接收线圈倾角均为45°)响应如图12。从图中可以看出,无论是传统随钻电磁波测井还是随钻方位电磁波测井,在钻井液电阻率低至0.1 Ω·m时,其受仪器偏心影响严重,而钻井液电阻率大于0.5 Ω·m时,基本不再受仪器偏心影响。

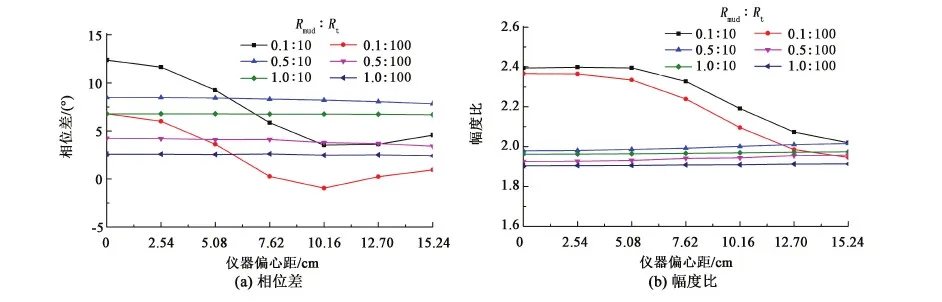
图11 传统随钻电磁波偏心响应Fig.11 Eccentric response of conventional LWD

考虑钻井液电阻率为0.1 Ω·m,线圈距为[78.74 93.98] cm条件下不同发射频率时,电磁波测井响应如图13。可以看出,随着仪器频率的降低,相位差和幅度比受偏心影响减弱;仪器频率大于2 MHz时,电磁波测井响应受仪器偏心影响严重;仪器频率低于400 kHz时,电磁波测井响应基本不受仪器偏心影响。考虑高频条件下,井眼环境变化对响应有较大的影响,讨论井径变化对电磁波测井响应影响。

对仪器居中及贴井壁模型,计算线圈距[55.88 71.12] cm,频率2 MHz的传统随钻电磁波与随钻方位电磁波测井仪器响应,结果如图14所示。仪器居中时,相位差和幅度比都随着井眼半径的增大而增大,而贴井壁测量时,相位差和幅度比随井眼半径呈非线性变化,随着井眼半径增大,其先增大后减小,相比之下,随钻方位电磁波受井眼半径影响更为复杂。因此,在井眼尺寸显著变化条件下进行仪器偏心校正及测井资料解释时,应当结合数值计算确定井径的影响程度。

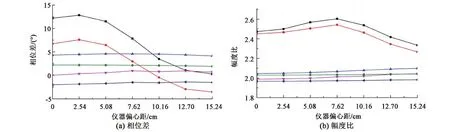
图12 随钻方位电磁波偏心响应Fig.12 Eccentric response of azimuthal LWD

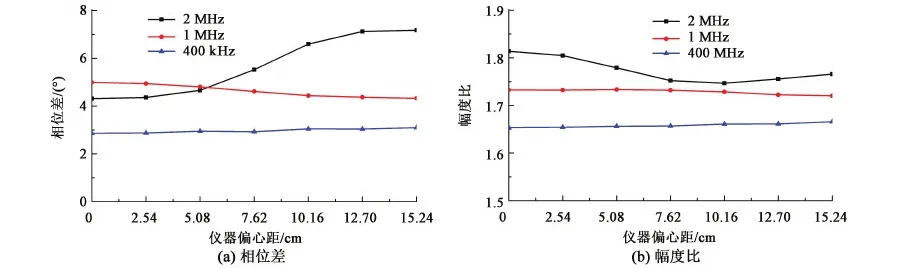
图13 不同频率响应Fig.13 Eccentric response with different transmitter frequencies

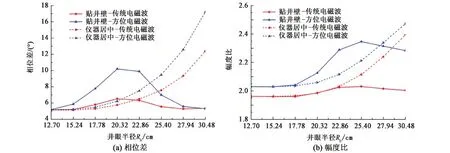
图14 不同井径电磁波测井响应Fig.14 Tool response of electromagnetic logging with different borehole sizes

3.3 方位信号

随钻方位电磁波测井的方位信号可用于识别地层边界,并判断仪器是由高阻目的层顶部穿出还是底部穿出,然而仪器偏心也会造成方位差异,产生方位信号。

设地层电阻率为10 Ω·m,钻井液电阻率为0.1 Ω·m,井眼半径为30.48 cm,线圈距为213.36 cm,利用方位角0°和180°的相位和幅度,提取方位信号,如图15所示。可以看出,仪器频率为100 kHz时,方位信号基本为0,且不随仪器偏心距变化。随着仪器频率的增高,方位信号受偏心影响增大,且随偏心距的增大,其影响增大。

进一步研究不同线圈距时方位信号变化,如图16。频率较低(小于400 kHz),线圈距较大(大于213.36 cm)时,方位信号基本不受仪器偏心影响,且随线圈距增大,受偏心影响减小;频率较高(2 MHz)的测量模式时,方位信号受仪器偏心影响严重。因此,对于随钻方位电磁波测井常用的低频长源距模式的400、100 kHz发射频率,213.36、243.84 cm的长源距数据,可忽略仪器偏心影响;而对于2 MHz,55.88和86.36 cm的高频短源距的电磁波数据,应当考虑仪器偏心对响应的贡献并做相应的校正。

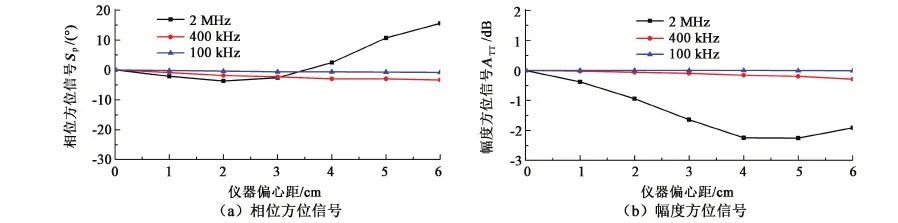
图15 不同频率下仪器方位信号Fig.15 Azimuthal signals with different transmitter frequencies

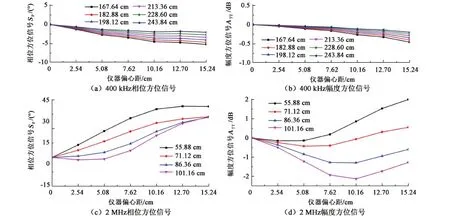
图16 不同线圈距方位信号Fig.16 Azimuthal signals with different spacing

不同井眼尺寸下仪器居中和贴井壁模拟结果如图17,图中展示了高频短源距模式和低频长源距模式的方位信号。可以看出，仅当井眼半径大于25.40 cm时,发射频率400 kHz的电磁波方位信号开始受到仪器偏心影响;而当井眼半径大于12.70 cm时,发射频率2 MHz、线圈距55.88 cm的方位信号已受井眼影响。因此,在进行地质导向时,低频长源距方位信号受井眼环境影响较小,可较好地反映地层界面信息,而高频短源距方位信号受井眼环境影响严重,井眼尺寸、仪器偏心程度等因素变化都会产生不可忽视的方位信号。

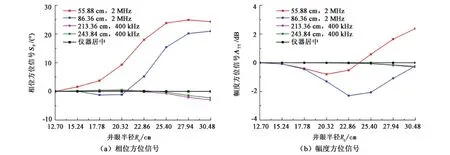
图17 不同井眼尺寸方位信号Fig.17 Azimuthal signals with different borehole sizes

4 结 论

(1)仪器偏心对随钻(方位)电磁波的影响与钻井液类型密切相关,油基钻井液钻井时,仪器偏心的影响可以忽略;水基钻井液钻井中,电阻率小于0.1 Ω·m时,响应受到仪器偏心影响,且仪器发射频率越高,受偏心影响越严重。

(2)水基钻井液条件下,仪器发射频率2 MHz时,随钻方位电磁波测井偏心响应受井眼影响严重,在进行地质导向和地层评价时,应当进行相应的校正;发射频率低至400 kHz时,随钻方位电磁波测井的方位信号基本不受仪器偏心及井径影响,可较好地用于随钻地质导向。

(3)利用随钻方位电磁波测井数据进行实时地质导向和地层评价时,应当首先确定钻井液类型、井眼尺寸以及测量仪器的参数,进而建立相应的模型进行仪器偏心校正,最终实现现场资料的处理解释。

[1] 汪宏年,商庆龙,朱天竹,等.用多分量感应资料快速重建层状地层的纵横向电阻率和水平界面深度[J]. 吉林大学学报(地球科学版), 2012,42(4):900-905.

WANG Hongnian, SHANG Qinglong, ZHU Tianzhu, et al. Simultaneously fast reconstruction of resistivities and interfaces in horizontally stratified TI formation by using multi component induction well logging data[J]. Journal of Jilin University (Earth Science Edition), 2012,42(4):900-905.

[2] 王磊,范宜仁,黄瑞,等.各向异性介质多分量感应测井三维Born几何因子理论研究[J].物理学报, 2015,64(23):438-448.

WANG Lei, FAN Yiren, HUANG Rui, et al. Three dimensional Born geometrical factor of multi-component induction logging in anisotropic media[J]. Acta Physica Sinica, 2015,64(23):438-448.

[3] LI Q M, OMERAGIC D, CHOU L, et al. New directional electromagnetic tool for proactive geosteering and accurate formation evaluation while drilling[C]. New Orleans, USA: SPWLA 46th Annual Logging Symposium, 2005.

[4] BITTAR M S, KLEIN J D, RANDY B, et al. A new azimuthal deep-reading resistivity tool for geosteering and advanced formation evaluation[J]. SPE Reservoir Evaluation & Engineering, 2009,12(2):270-279.

[5] OMERAGIC D, LI Q M, CHOU L, et al. Deep directional electromagnetic measurements for optimal well placement[C]. Dallas, TX: Society of Petroleum Engineers, 2005.

[6] 范宜仁,胡云云,李虎,等.随钻电磁波测井仪器偏心条件下响应模拟与分析[J].中国石油大学学报(自然科学版),2014,38(2):59-66.

FAN Yiren, HU Yunyun, LI Hu, et al. Numerical modeling and analysis of response of eccentric electromagnetics logging while drilling tool[J]. Journal of China University of Petroleum(Edition of Natural Science), 2014,38(2):59-66.

[7] HUE Y K, TEIXEIRA F L, MARTIN L S, et al. Three-dimensional simulation of eccentric LWD tool response in boreholes through dipping formations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005,43(2):257-268.

[8] 魏宝君,田坤,张旭,等.用并矢Green函数的矢量本征函数展开式评价偏心对随钻电磁波电阻率测井响应的影响[J].中国石油大学学报(自然科学版),2010,34(5):57-62.

WEI Baojun, TIAN Kun, ZHANG Xu, et al. Evaluating influence of eccentricity on response of electromagnetic wave resistivity logging-while-drilling by vector eigen function expansion formulae for dyadic Greens functions[J]. Journal of China University of Petroleum(Edition of Natural Science), 2010,34(5):57-62.

[9] LEE H O, TEIXEIRA F L, San Martin L E, et al. Numerical modeling of eccentered LWD borehole sensors in dipping and fully anisotropic earth formations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012,50(3):727-735.

[10] HUE Y K, TEIXEIRA F L. Analysis of tilted-coil eccentric borehole antennas in cylindrical multilayered formations for well-logging applications[J]. IEEE Transactions on Antennas and Propagation, 2006,54(4):1058-1064.

[11] HUANG F S, COOPE D, SHEN L C. The theory of 2 MHz resistivity tool and its application to measurement-while-drilling[J]. The Log Analyst, 1984,25(3):35-46.

[12] 高杰,辛秀艳,陈文辉,等.随钻电磁波电阻率测井之电阻率转化方法与研究[J].测井技术,2008,32(6):503-507.

GAO Jie, XIN Xiuyan, CHEN Wenhui, et al. Resistivity derivation in electromagnetic wave propagation resistivity logging while drilling[J]. Well Logging Technology, 2008,32(6):503-507.

(编辑 修荣荣)

Numericalmodelingandanalysisofeccentricityeffectonboreholeresponseofazimuthalelectromagneticloggingwhiledrillingtool

WU Zhenguan1,2, FAN Yiren1,2, WANG Lei1,2, LIU Jiaxiong1,2, XING Tao1,2

(1.SchoolofGeosciencesinChinaUniversityofPetroleum,Qingdao266580,China; 2.CNPCKeyLaboratoryforWellLogginginChinaUniversityofPetroleum,Qingdao266580,China)

In order to investigate the eccentricity effects of azimuthal resistivity LWD tools,the eccentric response is analyzed based on a staggered-grid finite-difference time-domain(FDTD) method. A conformal grid technology is implemented to obtain the effective conductivity of the complex boundary, and the algorithmis validated by comparing the results obtained by 3D-FDTD with the semi-analytic results. The electromagnetic field distribution is described under the centered and eccentric borehole conditions, and the signal law of dual coils configuration with different tool parameters and borehole environments is analyzed. Finally, the characteristics in the response and azimuthal signals of the LWD tool in eccentric borehole are investigated. The modeling results show that the eccentricity effects can be ignored in oil-based mud drilling, or water-based mud of which the resistivity is larger than 0.5 Ω·m. However, in water-based mud where the resistivity is less than 0.1 Ω·m, the eccentricity effects seem to correlate with the tool parameters. It is concluded that the long spacing and low frequency azimuthal signals can be used in geosteering directly, while the short spacing and high frequency azimuthal signals should be corrected to eliminate the borehole effects.

azimuthal resistivity LWD; eccentricity effect; 3D-finite-difference time-domain(FDTD); conformal grid

2016-09-01

国家自然科学基金项目(41474100, 41574118, 41674131)；山东省自然科学基金项目(ZR2013DM015)；中央高校基本科研业务费专项资金(17CX06041);中国石油大学(华东)研究生创新工程(YCX2017004,YCX2015003)

巫振观(1991-)，男，博士研究生，研究方向为电法测井快速正反演及电测井解释。E-mail：wuzg2014@163.com。

1673-5005(2017)05-0069-11

10.3969/j.issn.1673-5005.2017.05.008

P 631.8

A

巫振观,范宜仁,王磊,等. 随钻方位电磁波测井仪器偏心响应模拟及分析[J].中国石油大学学报(自然科学版),2017,41(5):69-79.

WU Zhenguan, FAN Yiren, WANG Lei, et al. Numerical modeling and analysis of eccentricity effect on borehole response of azimuthal electromagnetic logging while drilling tool[J].Journal of China University of Petroleum(Edition of Natural Science),2017,41(5):69-79.