基于声固耦合算法的发射模拟试验承压结构湿模态分析

陈炜彬, 段 浩, 王 云



基于声固耦合算法的发射模拟试验承压结构湿模态分析

陈炜彬, 段 浩, 王 云

(中国船舶重工集团公司第705研究所昆明分部, 云南昆明, 650106)

发射装置模拟试验承压结构——假海, 在试验过程中需要在其内部充水, 这种情况下的模态称为湿模态。文章通过充水管道的仿真结果同试验数据的对比, 验证了利用Workbench声学拓展模块进行基于声固耦合算法的结构湿模态仿真的可行性; 然后运用该方法对假海进行湿模态仿真, 并将结果同干模态仿真结果进行对比分析, 得到了充水对假海固有振动特性的影响, 为相关充液结构的湿模态研究提供参考。

假海; 声固耦合; 湿模态

0 引言

发射装置模拟试验承压结构[1]是一种在陆上模拟深海高压环境的试验设施, 主要由发射装置、筒体、循环水道、接收装置等设备组成, 以下简称假海。在实施发射装置陆上的模拟深海发射试验时, 假海通过充水并打压来实现对不同深度海洋环境的模拟。所以假海在实际工作时应视为储液容器, 对储液容器这种内部存有液体的结构, 湿模态才能准确地表征其动力学特性。为研究假海在发射冲击激励下, 结构的振动特性及对测试系统的影响, 文中对假海在充水状态下的湿模态进行研究。

在湿模态分析中, 流体对结构固有特性影响主要反映在2个方面: 首先是流体由于自身重力, 作用于流固交界面上的压力载荷, 而产生的预应力效应[2-3]; 其次是流体随结构运动而引起的附加质量效应[4-5]。由于假海的结构刚度较大, 预应力对假海振动特性的影响十分有限, 故文中主要研究附加质量效应对假海振动特性的影响。

目前对于结构湿模态的研究在各相关行业中已经得到普遍运用, 如: 姜峰等[6]对海洋立管的湿模态进行的仿真分析; 薛杰等[7]对充液容器进行了流固耦合模态分析; 陈先亮[8]对车用蓄水瓶进行了流固耦合动力学分析。

文中利用Workbench中的Acoustic Extension插件[6,9]通过声固耦合的方法分析假海的湿模态, 在分析过程中通过插件直接将水的附加质量加入到计算中, 简化了仿真计算过程。

1 湿模态分析

在实际的湿模态分析中, 由于相对振幅较小, 故结构服从胡克定律; 同时忽略空气和内部液体对结构振动的阻尼作用, 将充液结构视为无阻尼线性系统。通过有限元法离散化以后, 充液结构系统无阻尼自由振动[10]方程式为

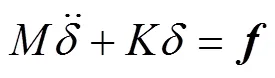
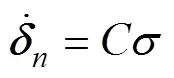
利用转换矩阵得到

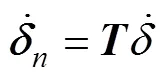
由式(2)和式(3)得

由虚功原理[12]得

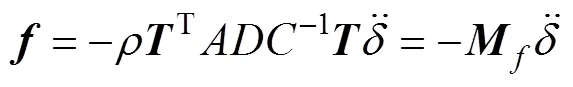
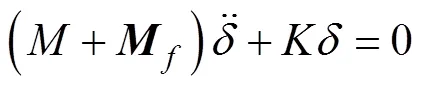
式(6)是考虑流体作用下的结构运动方程, 通过式(6)可进行结构湿模态分析。

2 声固耦合算法及验证

2.1 声固耦合理论

运用声固耦合算法进行湿模态分析时要把结构中的流体看成一种声学介质, 即一种弹性介质, 只需考虑流体体积应变的压力, 不考虑流体的粘性力。当结构振动时在流固交界面上对流体产生负载, 同时声压会对结构产生一个附加力, 为准确的模拟这种情况, 需要同时计算结构动力学方程和流体的波动方程来确定交界面上的位移和声压值。

接下来假设结构内的流体是理想的声学介质[13], 则波动方程为

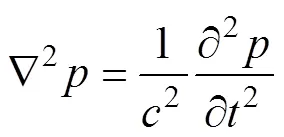
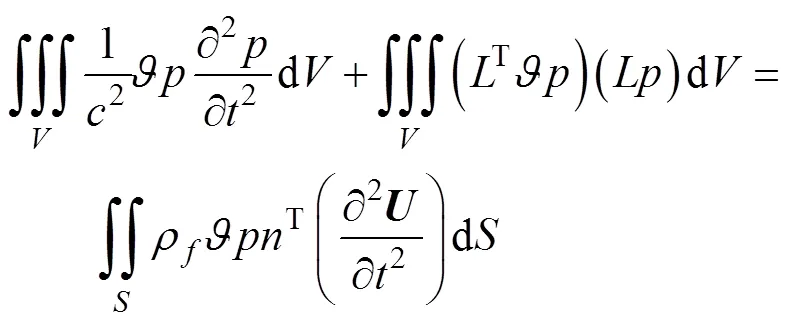
将流体方程离散化, 分成若干个有限单元, 用相应的插值表示单元的声压、质点位移等, 并约去声压变分, 可得到完全耦合的结构流体运动方程

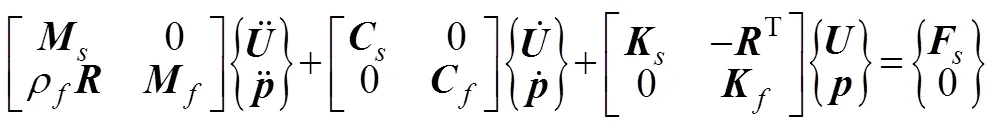
在分析中不考虑阻尼, 故将式(9)写成

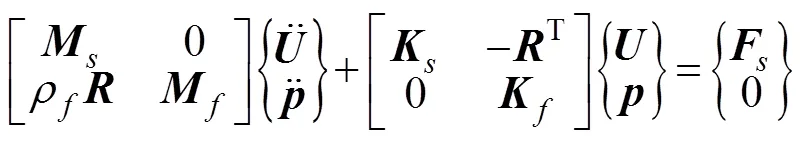
2.2 方法验证

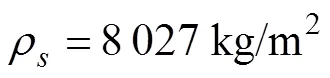
表1 测试结果

接下来通过Workbench对该模型进行干模态和湿模态的分析。在工作空间内建立共享同一模型的2个模态分析模块, 分别为湿模态分析模块和干模态分析模块。

在Workbench中建立充液管道模型, 将水的模型属性更改为Fluent, 管道模型保持为软件默认的Solid。在进行干模态分析时将水的模型抑制。

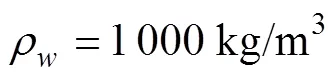
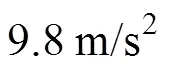
干模态分析的设置较为简单, 添加相应的边界条件即可, 设置完成后开始运算。得到计算结果见表2。

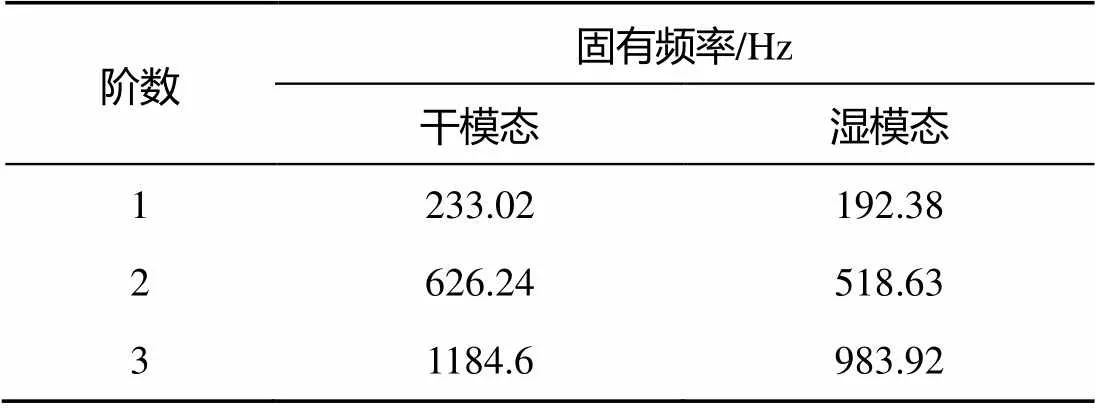
表2 仿真结果

通过试验和仿真的固有频率对比, 见表3。可以看到, 仿真得到的固有频率和实验测得的固有频率误差在3.5%以下, 湿模态的误差最高的只有2.54%, 所以可以认为仿真结果是准确的。这就说明使用声学拓展模块进行结构湿模态分析是可行的。

表3 试验与仿真对比

3 假海干湿模态对比分析

为了研究假海结构在充满水情况下的振动特性, 接下来用Workbench分别对假海在没有充水及充满水情况下的模态进行仿真分析, 并进行对比。

文中分析的对象——假海, 其整体结构长度30 m, 宽度11 m, 高度6.5 m; 筒体两支座之间距离为8.9 m; 主体结构内径为6 m; 循环水道安装中心线位置距接收管安装端面为7.1 m, 具体外形见图1。

图1 3D简化模型

在Workbench中建立关联分析模块, 使得干模态和湿模态共用一个模型, 在进行干模态分析时将水模型抑制。Acoustic Extension部分的设置同第2章中的设置相同, 在此基础上设置假海的固定约束和重力加速度等。

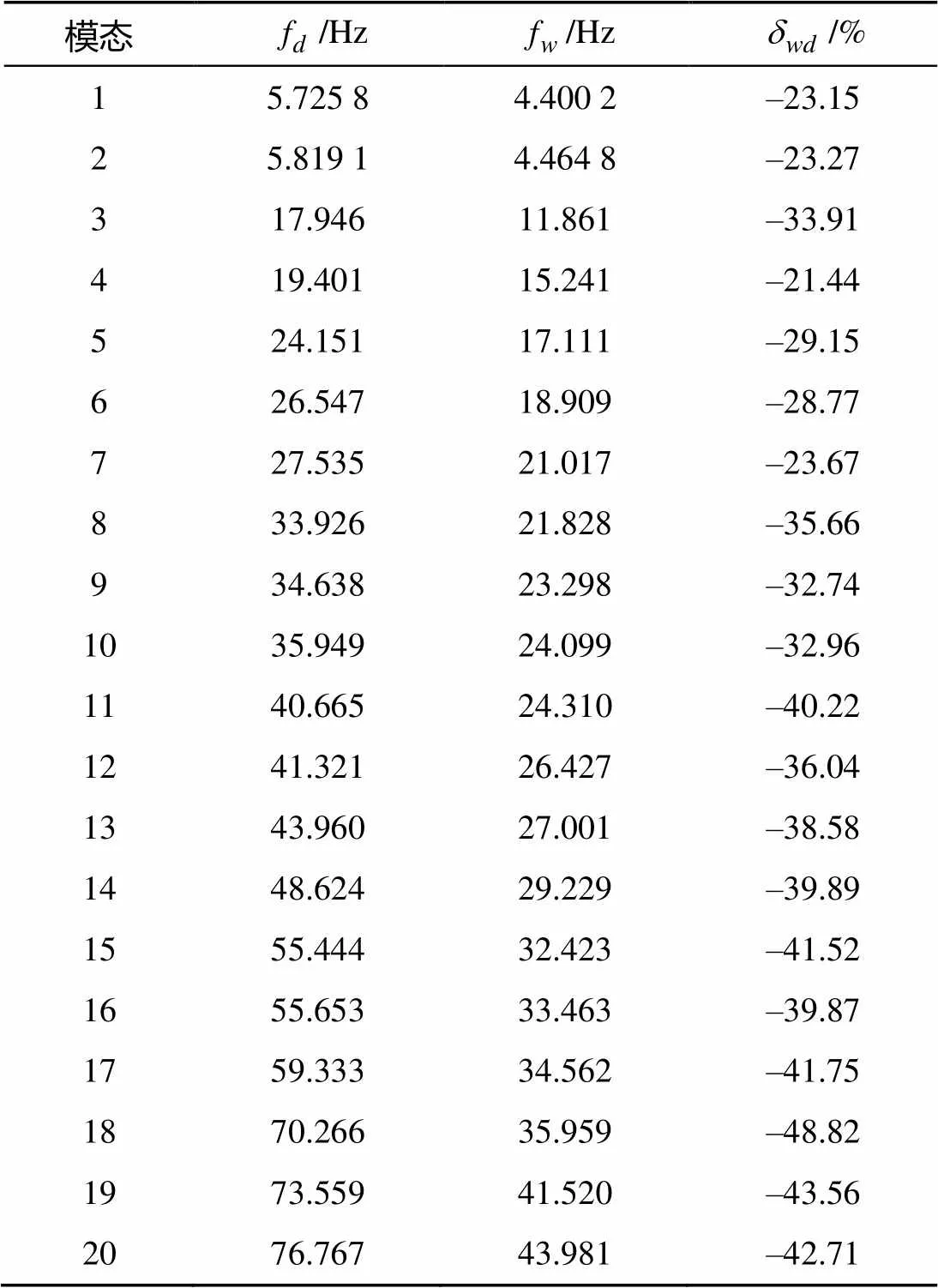
表4 假海干湿模态仿真结果对比

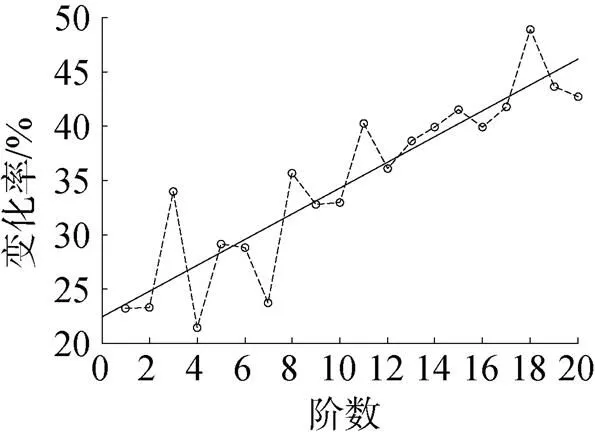
图2 变化率折线图

通过观察变化率折线图可以看到, 从1阶模态到20阶模态, 固有频率变化率总体上随着模态阶数的提高而逐渐增大, 中间略有波动, 这一趋势符合充水管道的试验结果。可以推断水的流固耦合作用对结构固有频率的影响和结构振动的频率存在内在的关联, 当干模态状态下结构固有频率越大, 湿模态状态下该固有频率下降的比率就越高, 如图3所示。

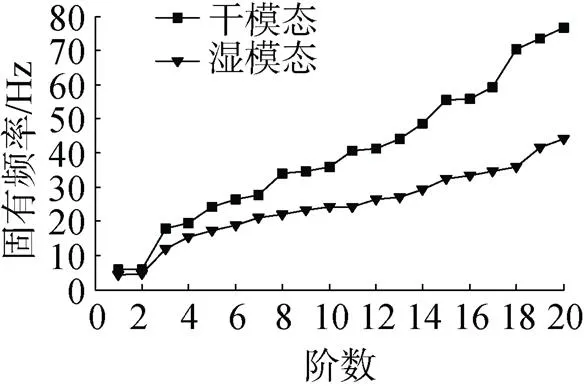
图3 干模态和湿模态固有频率变化趋势

图3的变化趋势说明, 水对结构振动的影响和振动的频率有关, 所以干模态固有频率越高,对应的湿模态固有频率相对下降的比率就越高。

如表5所示, 总体上湿模态各阶模态的最大变形量要小于干模态, 但是第5、12、13阶模态对应的变形量却要大一些。理论上当容器内充满水时, 容器受到水的作用, 其固有频率下降, 对应的振动幅度也会相应减小。通过对比2种状态下的假海振型, 如图4所示可以发现, 第5阶振型发生局部的改变, 假海筒体的振动显著减小,振动集中在循环水道且振动幅度变大; 第12、13阶的振型发生显著的改变, 从假海整体振动变为接收管局部振动, 振动幅度也相应变大。综上, 假海在水的作用下固有振型发生了变化, 导致假海某些模态的最大振幅变大。

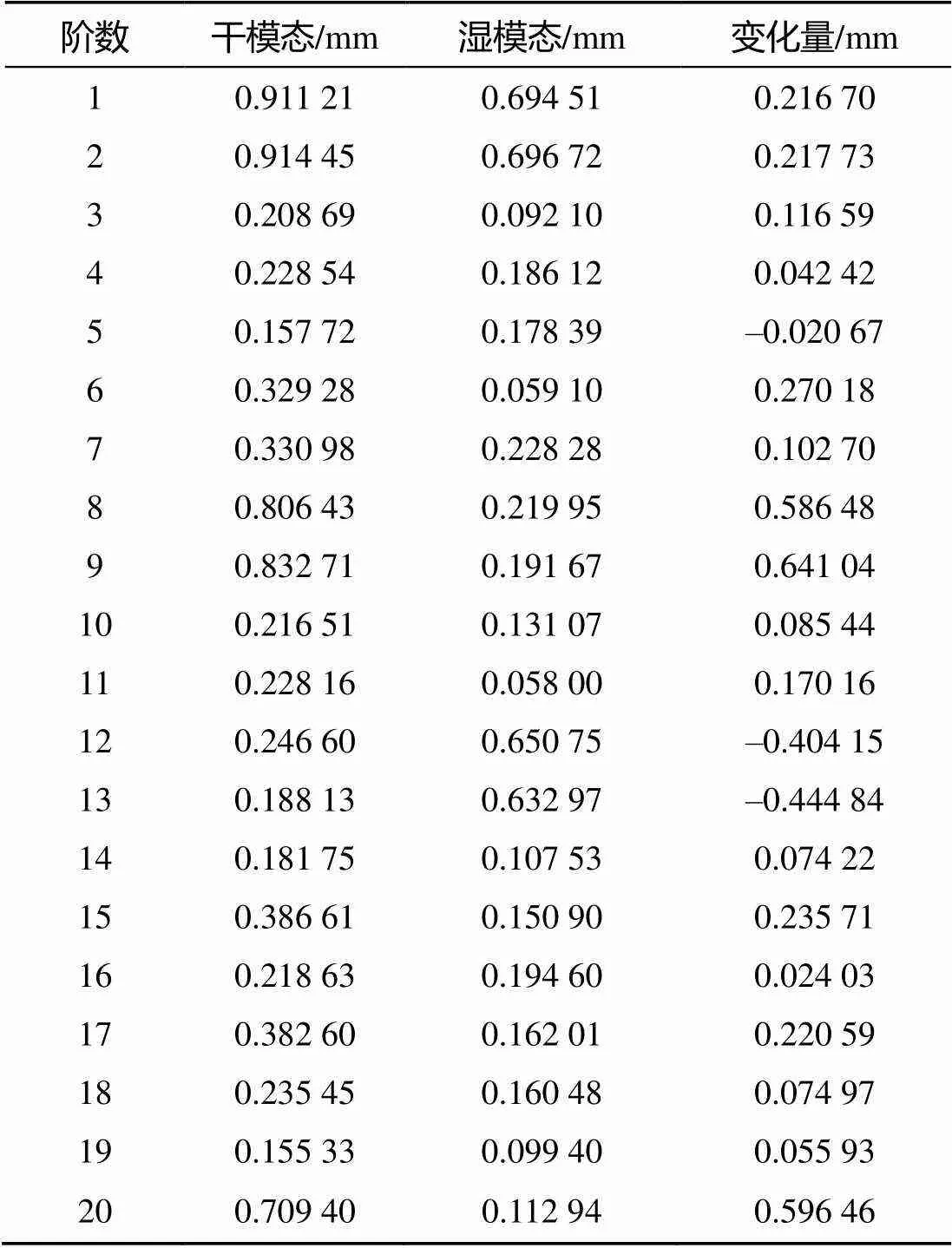
表5 各阶模态变形量对比

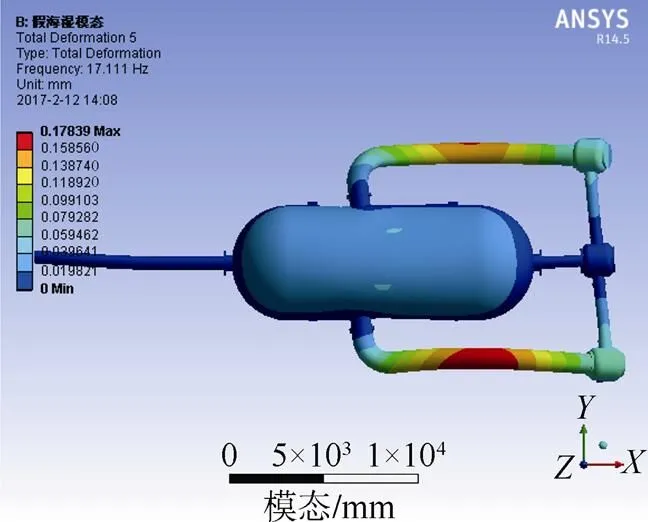
综合上述分析得出, 水对假海的振动特性存在巨大的影响, 不但降低了假海的固有频率, 还改变了某些模态的固有振型。

4 结论

文中首先验证了通过Workbench中的Acoustic Extension插件进行基于声固耦合算法的湿模态分析是可行的, 且具有较高的精度。并运用该方法对假海进行了湿模态的仿真分析, 将分析结果同干模态进行对比得出以下结论:

1) 充水对假海结构的振动特性具有显著的影响, 水的存在大大降低了结构的固有频率, 下降比例在–21.44% ~ –48.82%之间, 且固有频率下降比率总体同阶数成正比, 这一规律是符合液体对结构振动影响趋势的;

2) 充水使得假海相同振型的振动幅值变小,也使假海的某些固有振型发生改变, 从而使得振动幅度最大值发生异常变化, 故在假海设计时应充分考虑水对结构振动特性的影响。

[1] 段浩, 李经源. 鱼雷发射技术[M]. 北京: 国防工业出版社, 2015.

[2] 王昆, 刘进福, 韩晶, 等. 基于ANSYS Workbench的焊接机器人大臂预应力模态分析[J]. 机械工程师, 2014(2): 159-160.Wang Kun, Liu Jin-fu, Han Jing, et al. Pre-stressed Modal Analysis of the Welding Robot Arm Based on ANSYS Workbench[J]. Mechanical Engineer, 2014(2): 159-160.

[3] 李小彭, 赵光辉, 杨皓天, 等. 考虑结合面影响的组合梁非线性预应力模态分析[J]. 振动与冲击, 2014, 33(4): 17-21.Li Xiao-peng, Zhao Guang-hui, Yang Hao-tian, et al. Nonlinear Pre-stressed Modal Analysis for a Composite Beam Considering Influence of Joint Surface[J]. Journal of Vibration and Shock, 2014, 33(4): 17-21.

[4] 张光法. 潜深对半潜器附加质量影响分析[J]. 舰船电子工程, 2012, 32(11): 9-10.Zhang Guang-fa. Analysis of Influence of Submerged Depth on Adds Mass of Semi-submerged Device[J]. Ship Electronic Engineering, 2012, 32(11): 9-10.

[5] 李明, 尹云玉. 水下航行体动态响应计算的附加质量探讨[J]. 导弹与航天运载技术, 2008(4): 16-18.Li Ming, Yin Yun-yu. Effect of the Added Mass on Transverse Response Calculation of Submarine Vehicle in Exiting-water Process[J]. Missile and Space Vehicle, 2008(4): 16-18.

[6] 姜峰, 郑运虎, 梁瑞, 等. 海洋立管湿模态振动分析[J]. 西南石油大学学报自然科学版, 2015, 37(5): 159-166.Jiang Feng, Zheng Yun-hu, Liang Rui, et al. An Analysis of the Wet Modal Vibration of Marine Riser[J]. Journal of Southwest Petroleum University, 2015, 37(5): 159-166.

[7] 薛杰, 何尚龙, 杜大华, 等. 充液容器流固耦合模态仿真分析研究[J]. 火箭推进, 2015, 41(1): 90-97. Xue Jie, He Shang-long, Du Da-hua, et al. Study on Fluid-structure Coupling Modal Simulation of Liquid Filling Container[J]. Journal of Rocket Propulsion, 2015, 41(1): 90-97.

[8] 陈先亮. 基于流固耦合的车用蓄水瓶动力学分析[D]. 重庆: 重庆大学, 2014.

[9] 张双狮. 波纹管管道振动特性分析及测试[D]. 武汉: 武汉轻工大学, 2015.

[10] 杨鸣, 王辉, 段玉康, 等. 基于声-固耦合算法的储液容器湿模态分析[J]. 四川兵工学报, 2015, 36(5): 152-154.Yang Ming, Wang Hui, Duan Yu-kang, et al. Wet Mode Analysis of Liquid Storage Containers Based on Acoustic Structure Coupling Method[J]. Journal of Sichuan Ordnance, 2015, 36(5): 152-154.

[11] 马佳男. 格林函数在平面近场声全息技术中的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.

[12] 王焕定. 再论变形体虚功原理[J]. 力学与实践, 2011, 33(2): 93-95.Wang Huan-ding. The Deformation Principle of Virtual Work Theory Again[J]. Mechanics in Engineering, 2011, 33(2): 93-95.

[13] 缪旭弘, 钱德进, 姚熊亮, 等. 基于ABAQUS声固耦合法的水下结构声辐射研究[J]. 船舶力学, 2009, 13(2): 319-324.Miao Xu-hong, Qian De-jin, Yao Xiong-Liang, et al. Sound Radiation of Underwater Structure Based on Coupled Acoustic-structural Analysis with ABAQUS[J]. Journal of Ship Mechanics, 2009, 13(2): 319-324.

[14] 商德江, 何柞镛. 加肋双层圆柱壳振动声辐射数值计算分析[J]. 声学学报, 2001, 26(3): 193-201.Shang De-jiang, He Zuo-yong. The Numerical Analysis of Sound and Vibration from a Ring-stiffened Cylindrical Double-shell by FEM and BEM[J]. Acta Acustica, 2001, 26(3): 193-201.

[15] 姚煜中. 充液管道动力学建模与振动特性分析[D]. 上海: 上海交通大学, 2011.

(责任编辑: 许 妍)

Wet Modal Analysis of Pressurized Structure in Launcher SimulationExperiment Based on Sound-Structure Coupling Algorithm

CHEN Wei-bin, DUAN Hao, WANG Yun

(Kunming Branch of the 705 Research Institute, China Shipbuilding Industry Corporation, Kunming 650106, China)

During launcher simulation experiment, the pressurized structure called false sea, is internally filled with water, the modal in this case is called wet modal. In this paper, the simulated and experimental results of a tube full of water are compared to prove the feasibility that the Workbench acoustic extension module can be used to carry out wet modal simulation based on the sound-structure coupling algorithm. Then, the method is employed to simulate the false sea′s wet modal. The simulation results of wet modal and dry modal are compared to obtain the influence of water on the natural vibration characteristic of false sea. This study may provide a reference for the research on wet modal of water-filled structures.

false sea; sound-structure coupling; wet modal

陈炜彬, 段浩, 王云. 基于声固耦合算法的发射模拟试验承压结构湿模态分析[J]. 水下无人系统学报, 2017, 25(4): 365-370.

TJ635

A

2096-3920(2017)04-0365-06

10.11993/j.issn.2096-3920.2017.04.010

2017-02-15;

2017-02-28.

陈炜彬(1991-),男, 在读硕士, 主要从事鱼雷发射技术研究.