角接触球轴承径向刚度仿真

李传喜, 段 浩, 王 云



角接触球轴承径向刚度仿真

李传喜, 段 浩, 王 云

(中国船舶重工集团公司第705研究所昆明分部, 云南昆明, 650118)

角接触球轴承是涡轮泵发射系统中的关键元件之一。轴承的径向支撑刚度对涡轮泵发射系统的性能有着十分重要的影响, 为了获取可靠的轴承径向支撑刚度, 以Hertz接触理论和轴承几何关系为基础, 推导了角接触球轴承径向刚度计算模型, 考虑了系统轴向预紧载荷与径向载荷的耦合作用、径向间隙和过盈量, 分析了不同因素对轴承径向刚度的非线性影响规律。文中的分析结果可为旋转机械整体分析提供参考。

涡轮泵发射系统; 角接触球轴承; 径向刚度

0 引言

滚动轴承广泛应用于机械系统中, 是决定整个机械系统性能的关键元件之一[1]。在早期, 人们把滚动轴承处理为一个简单的线性模型, 但在工程实践中, 线性模型不能解释轴承元件间接触力与变形之间的非线性关系[2]。20世纪60年代, Jones提出了滚动轴承滚道控制理论用于解决滚动轴承动态性能分析问题。Harris结合弹性流体润滑理论首次建立了滚动轴承拟静力学分析模型, 分析了滚子和保持架的运动状态。Walters和Gupta先后建立了轴承动力学分析模型, 通过引入运动微分方程来描述轴承任意时刻的运动状态, 并用数值方法计算轴承元件的瞬态动力学特性[3]。但是, 无论是静力学分析方法, 还是动力学分析方法, 模型都较为复杂, 有些参数还需要通过试验确定, 而且计算机编程麻烦, 需要大量的求解时间。如果仅仅想获得轴承的支撑刚度, 目前普遍采用的是经验公式。

以往的轴承径向刚度经验公式计算中, 一般只考虑轴承所受的预紧力, 忽略轴承接触角的改变量和过盈配合量的影响, 也经常忽略轴承径向间隙的作用。文献[4]和文献[5]重新研究了轴承刚度计算公式, 但是没有考虑轴向载荷与径向载荷的耦合, 也没有考虑轴承在受载时参数的变化。在径向刚度计算中, 油膜的作用很复杂, 如果仅仅计算油膜的刚度与Hertz接触刚度的叠加, 轴承的径向刚度是减小的, 但是油膜的存在使滚动体与滚道之间的接触面积增大, 这一改变又使得刚度增加, 这个增加量很难计算。依照文献[6]给出的结论, 油膜对轴承刚度有一定的提升, 但提升的幅度不到1%, 所以文中忽略油膜的作用。

文章从Hertz接触理论和轴承几何关系出发, 考虑轴承轴向预紧力、径向间隙、过盈量、接触角和径向载荷的变化, 推导了角接触球轴承径向刚度计算模型, 验证了模型的可靠性, 分析了预紧力、径向载荷等因素对球轴承径向刚度的影响。

1 Hertz点接触理论

1.1 基本假设

Hertz点接触问题描述2个曲面弹性体仅在一点接触的情况, 接触区域内的应力应变具有局部性质, 即它们随着离开接触点距离的增大而迅速衰减。Hertz理论成立需依赖以下假设条件:

1) 两接触物体均为各向同性线弹性体, 接触区域满足小变形条件;

2) 接触区域表面为连续光滑表面, 载荷完全垂直于接触表面, 接触区域不存在摩擦;

3)接触区域的长半轴相对于物体接触区域的曲率半径是很小的, 满足弹性力学半空间基本解的条件, 可以应用半空间基本解分析力和位移。

1.2 弹性半空间基本解

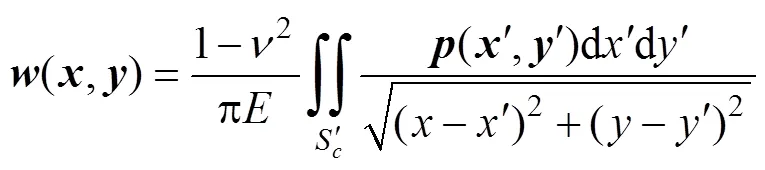
图1 压力p椭球分布

Fig. 1 Ellipsoidal distribution of pressure p

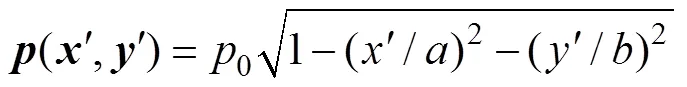
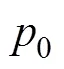
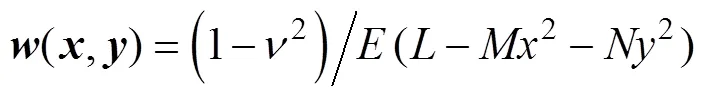
上式中各参数如下

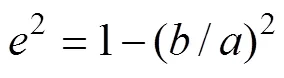
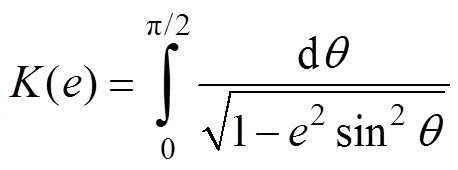
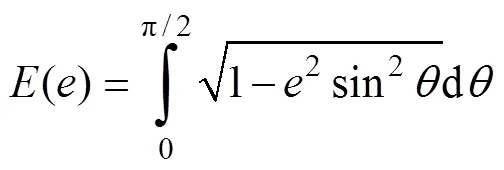
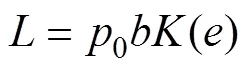
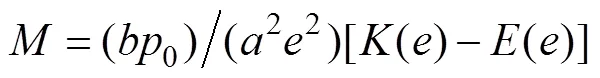
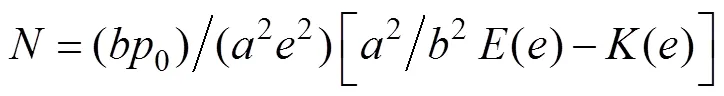
1.3 几何描述

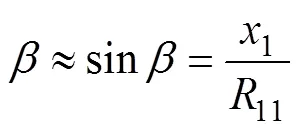
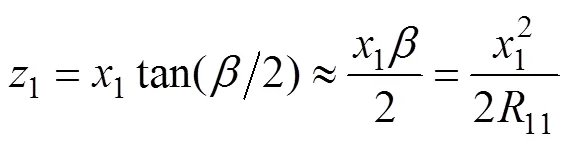
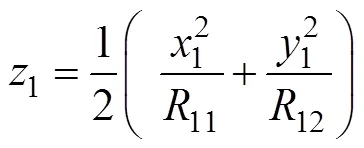
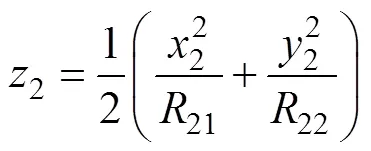
则这两点之间的距离为

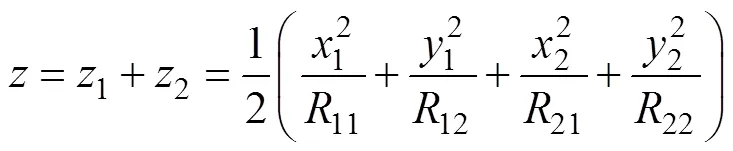
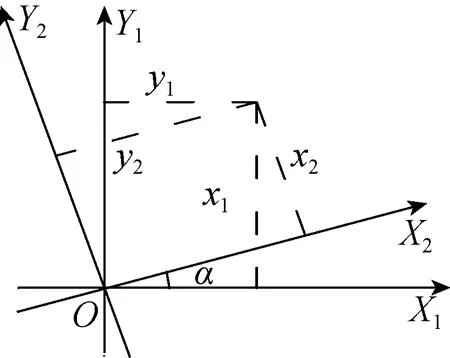
图3 坐标变换

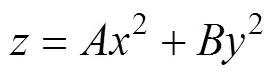
1.4 基本方程

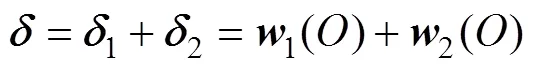
将式(1)、式(3)和式(15)代入式(16), 得

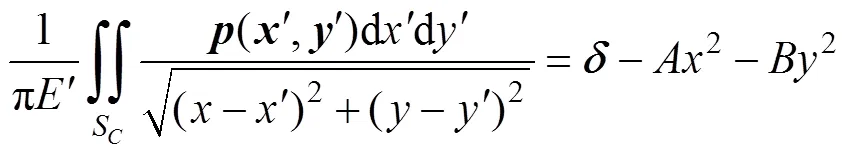
其中

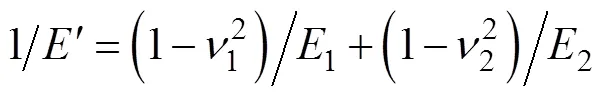
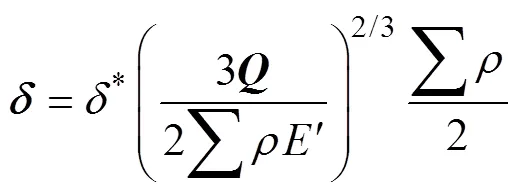
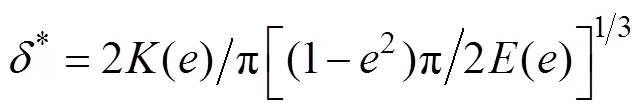
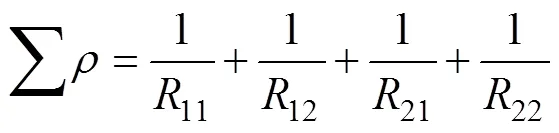
当运用数值计算方法解上述方程时, 比较耗时。Hamrock和Dowson[8]通过曲线拟合的方法给出了一组点接触问题的近似公式, 大大简化了计算。公式如下

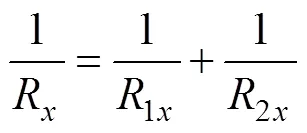
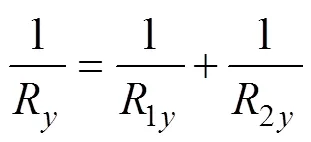
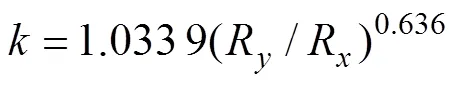
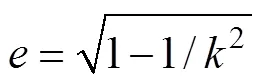
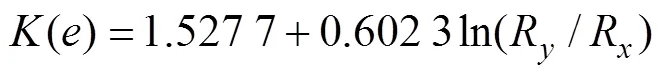
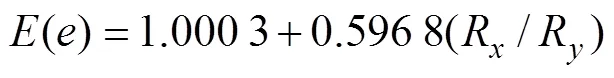
由上述计算得出的值, 与文献[4]给出的结论相比较, 误差不超过3%。

2 球轴承几何量计算

2.1 几何关系

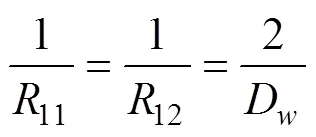
对于内滚道, 沟道曲率为(负号表示内滚道是凹陷曲面)

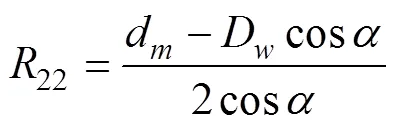
对于外滚道, 在纸平面内的沟道曲率为

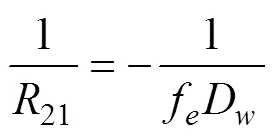
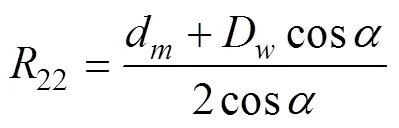
2.2 径向间隙

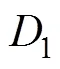
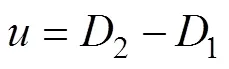
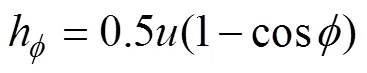
2.3 轴承过盈配合量及由过盈配合引起的接触 角变化

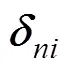
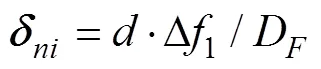
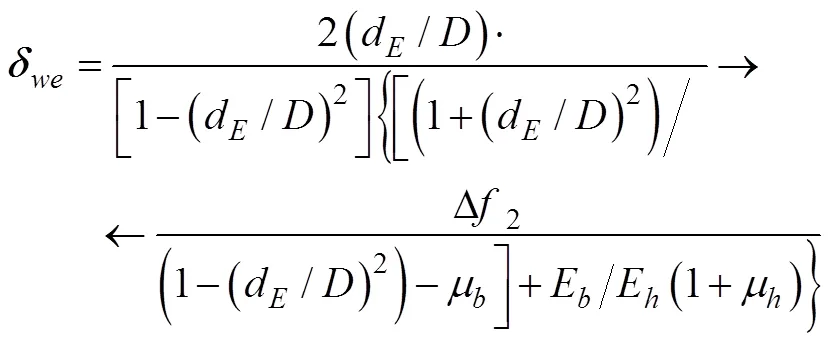
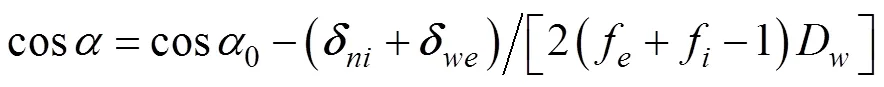
3 球与滚道之间载荷位移的关系

为了便于轴承的计算分析, 一般采用了刚性套圈假设, 即假设轴承在受载时内外套圈只表现为与滚动体接触区域的局部变形, 内外套圈的整体形状不发生变化, 依然为圆形套圈。这一假设大大简化了分析计算, 而且在一般情况下, 分析结果是完全可以接受的[4]。

式中,为柔度系数。钢球与2个滚道之间总的法向趋近量为

则有

3.1 轴向预紧载荷作用下的接触角计算

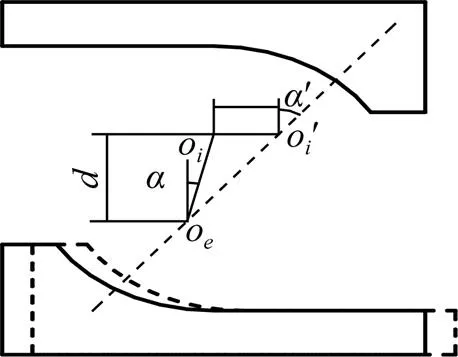
图5 轴向变形

由图5可知

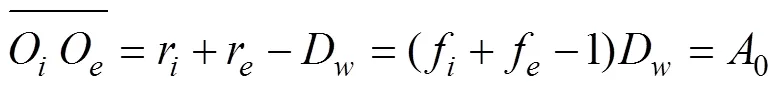
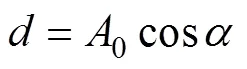
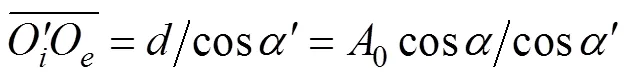
钢球与内、外滚道之间的法向接触变形为

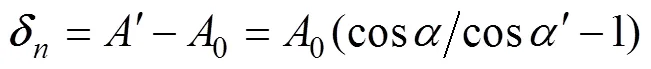
有轴承的平衡方程可以推导得

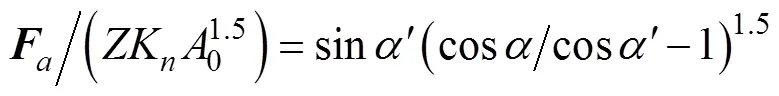
3.2 单个球轴承刚度受轴向预紧载荷和径向载荷的计算模型

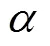
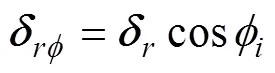
考虑到钢球与滚道之间的初始间隙和过盈量, 轴向预紧载荷引起的变形, 钢球与滚道之间总的接触变形为

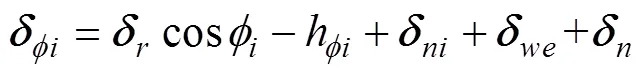
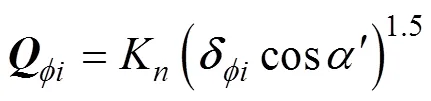
轴承的平衡方程为

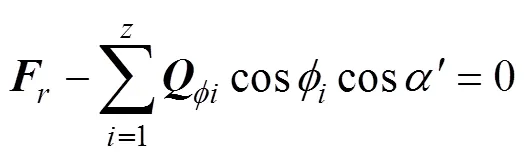
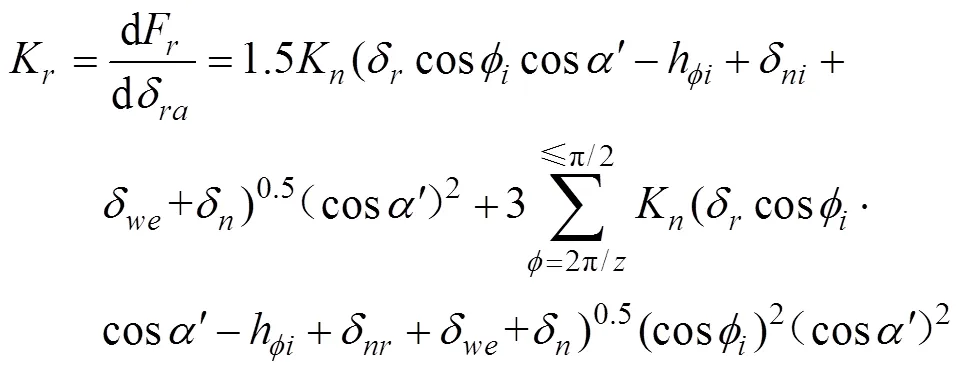
由上式可以看出, 轴承径向刚度不是一个常量, 它会随着位移的变化而变化。因此在提到轴承刚度时, 应指出与它对应的位移或载荷, 否则就没有意义。

4 模型验证

为了验证模型的正确性, 文中借鉴文献[9]和文献[10]的实验数值, 对7020C、7020A、7015C在不同预紧力下的径向刚度进行了仿真计算, 如表1所示, 相对误差基本在15%以内, 能够满足工程计算的需要。

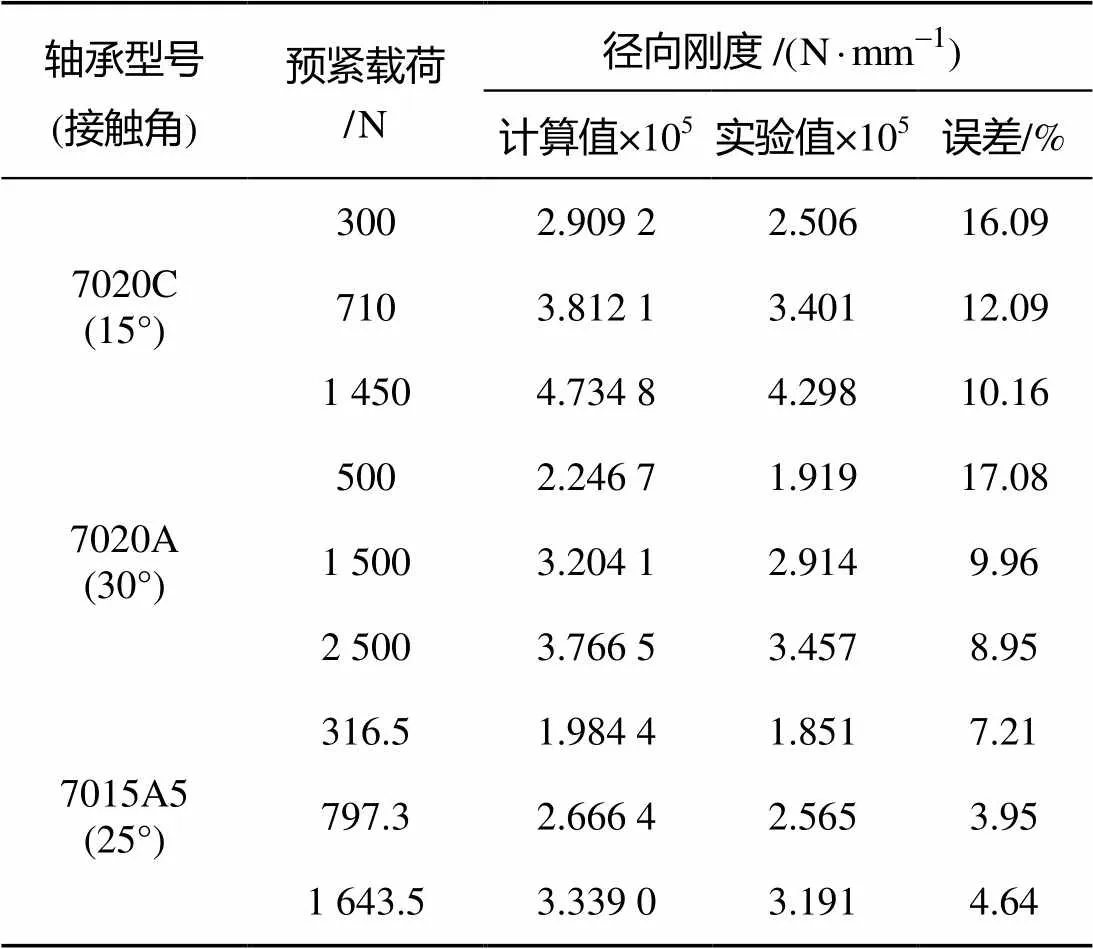
表1 理论计算与实验结果对比

5 轴承径向刚度影响因素

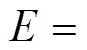
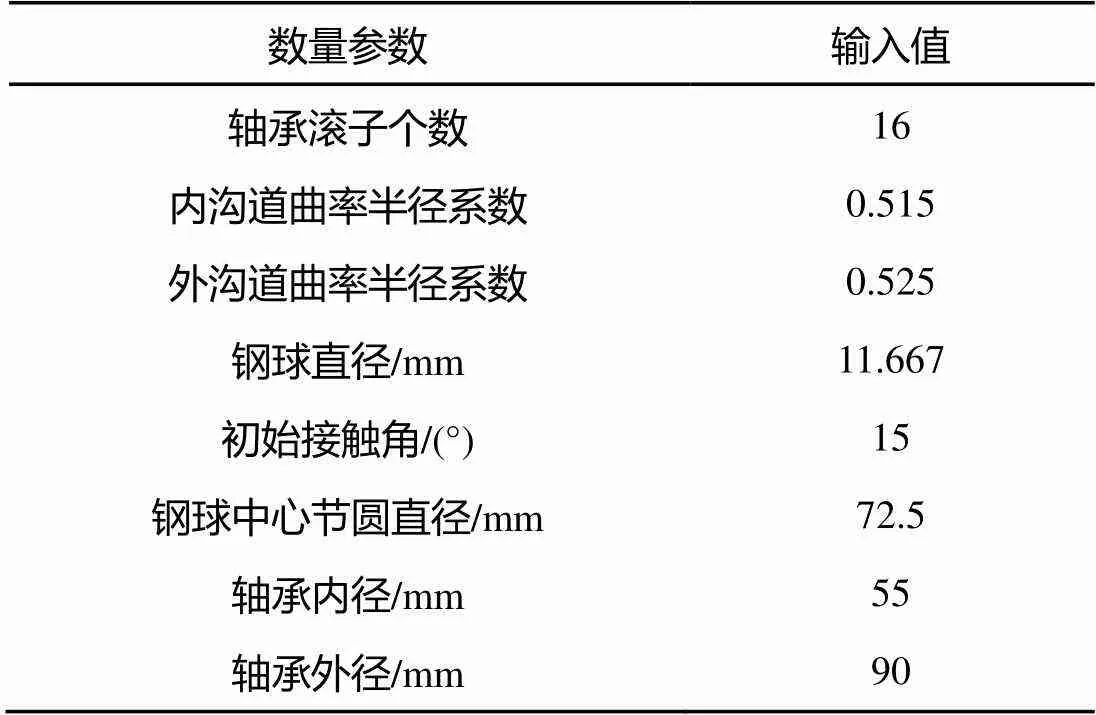
表2 7011C轴承初始参数

5.1 轴承径向刚度随轴向预紧载荷的变化

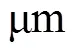
表3 径向刚度与轴向预紧载荷的关系

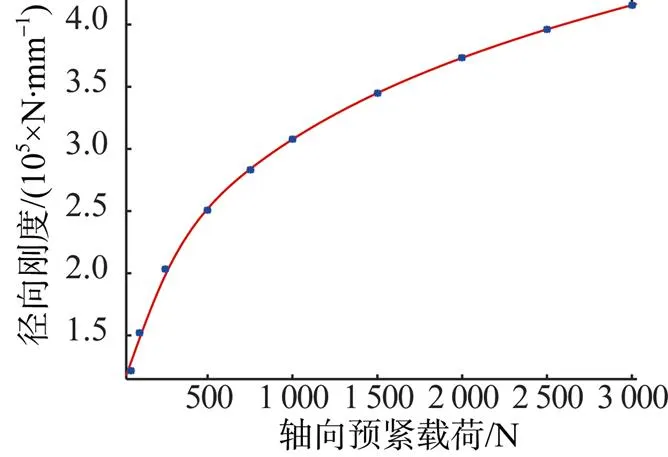
图6 径向刚度随轴向预紧载荷的变化

5.2 轴承径向刚度随轴承径向间隙的变化

轴承间隙是轴承的重要参数, 间隙包括轴向间隙和径向间隙, 轴承安装后轴向间隙一般很小, 且随着轴向预紧载荷的增大而减小, 可以不用考虑。径向间隙包括初始安装间隙和轴承磨损间隙, 如果轴承径向间隙过大, 将严重影响轴承的动态性能, 增大旋转机械的振动和噪声, 必要时必须替换掉径向间隙过大的轴承。径向间隙对于轴承径向刚度的影响如表4和图7所示, 此时轴向力为200 N、过盈量为零, 在轴承工作的初期, 随着径向间隙的增大, 轴承径向刚度急剧降低, 随着径向间隙的进一步增大, 径向刚度降低的速率减小, 曲线是非线性的。

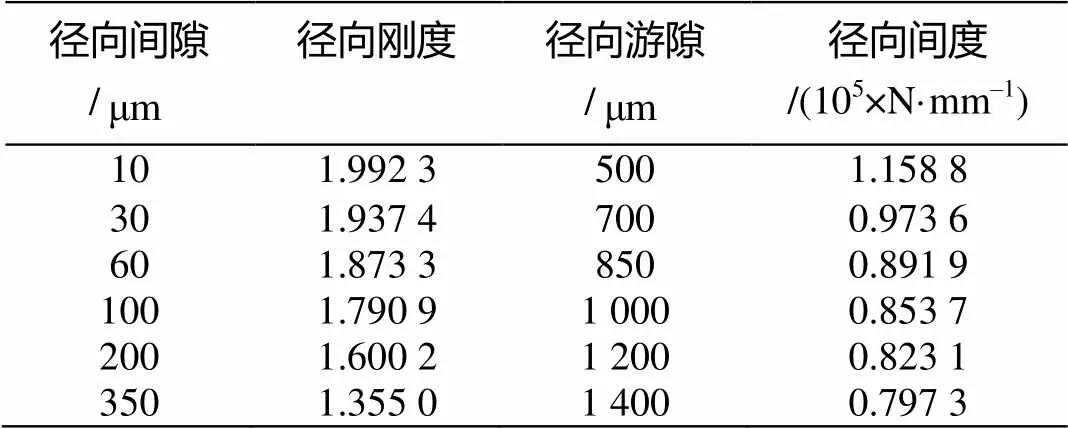
表4 径向刚度与径向间隙的关系

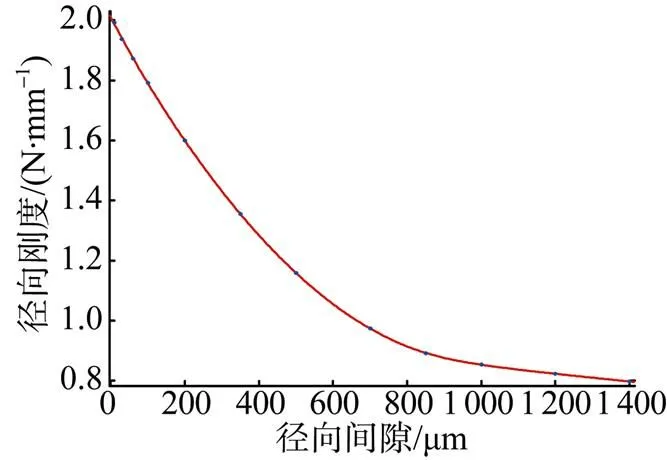
图7 径向刚度随径向间隙的变化

5.3 轴承径向刚度随安装过盈量的变化

表5 径向刚度与过盈量的关系

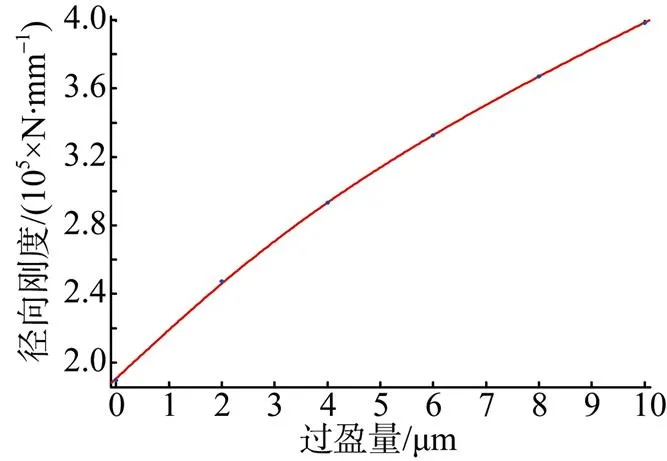
图8 径向刚度随过盈量的变化

5.4 轴承径向刚度在轴向预紧载荷和径向载荷耦合作用下的变化

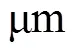
随着径向弹性变形的增大, 轴承径向刚度增大, 曲线也是非线性的。在有轴向预紧载荷的曲线上, 存在一个极大值和一个极小值。在仿真计算过程中, 发现在极大值附近的径向位移反方向上的滚动体接触距离出现了负值或零值。由接触理论知, 接触距离为负值或零值, 接触力为零, 不存在接触力为负值的情况, 所以计算过程中对接触力为负值的滚动体予以剔除, 不参与运算。从极大值到极小值的过程中, 在仿真运算中发现, 轴承滚动体所受负载荷或零载荷的数目一直增加, 到极小值时, 轴承中只有径向位移方向下半部分内的滚动体受力, 且随着径向载荷的增加, 也只有这一半滚动体受力。可以证明, 随着轴向载荷的增加, 极大值和极小值所对应的横坐标的位置向右移, 当轴向载荷足够大或径向位移足够小时, 极小值和极大值将相继不再出现。

表6 径向刚度(200 N轴向预紧载荷)与径向弹性变形的关系

表7 径向刚度(100 N轴向预紧载荷)与径向弹性变形的关系

表8 径向刚度(无轴向预紧载荷)与径向弹性变形的关系

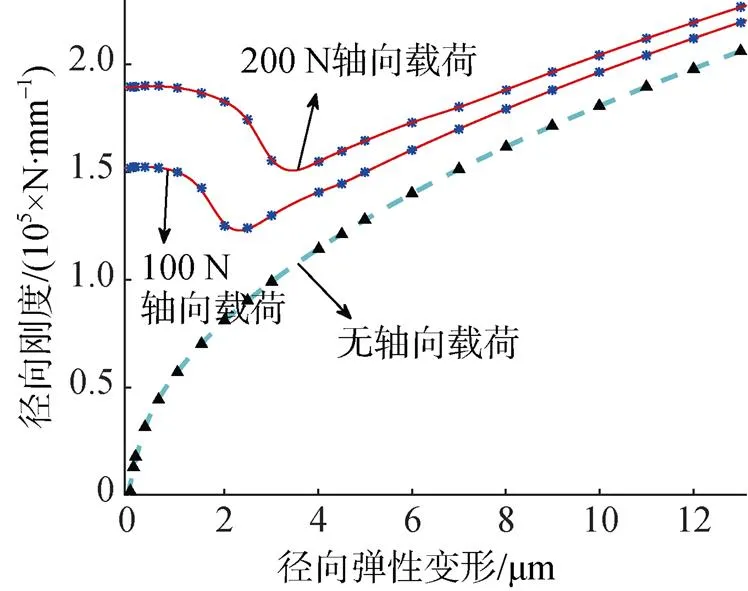
图9 径向刚度随径向弹性变形的变化

6 结论

文中根据Hertz接触理论, 重新推导了角接触球轴承径向刚度计算模型, 验证了模型的可靠性, 并通过理论计算, 分析了轴向预紧载荷、径向间隙和过盈量对角接触球轴承径向刚度的非线性影响规律, 以及轴向预紧载荷和径向载荷耦合作用下的轴承的径向刚度的变化规律。得到如下结论。

1) 文中建立模型相对误差基本在15%以内, 基本能够满足工程计算的需要。

2) 随着轴向预紧载荷的增大, 轴承径向刚度增大; 随着径向间隙的增大, 轴承径向刚度减小; 随着过盈量的增大, 轴承径向刚度增大。这3种情况轴承径向刚度的变化规律是非线性的, 变化率是逐渐减小的。

3) 轴向预紧载荷的存在可大幅度的提高径向位移较小时的轴承径向刚度, 可有效的减小机器的振动。

[1] 马国华, 胡桂兰. 滚动轴承弹性接触问题的数值计算[J]. 轴承, 2005(1): 1-3.Ma Guo-hua, Hu Gui-lan. Numerical Calculation of Elastic Contact Problem of Rolling Bearings[J]. Bearings, 2005(1): 1-3.

[2] Tandon N, Choudhury A. A Review of Vibration and Acoustic Measurement Methods for the Detection of Defects in Rolling Element Bearings[J]. Tribology International, 1999, 32(2): 469-480.

[3] 邓四二, 贾群义, 薛进学. 滚动轴承设计原理[M]. 第2版. 北京: 中国标准出版社, 2014.

[4] 罗继伟, 罗天宇. 滚动轴承分析计算与应用[M]. 北京: 机械工业出版社, 2009.

[5] 陈时锦, 张春玉. 轴承刚度矩阵的解析推导与计算机求解[J]. 轴承, 2006(2): 1-4.Chen Shi-jin, Zhang Chun-yu. Analytic Deduction and Computer Solution of Bearing Stiffness[J]. Bearing, 2006(2): 1-4.

[6] 杜秋华, 杨曙年. 考虑润滑和波纹度影响的球轴承径向刚度[J]. 振动与冲击, 2007, 26(10): 152-156.Du Qiu-hua, Yang Shu-nian. Radial Stiffness of Ball Bearing Considering the Influence of Lubrication and Waviness[J]. Vibration and Shock, 2007, 26(10): 152-156.

[7] 钱伟长, 叶开源. 弹性力学[M]. 北京: 科学出版社, 1980.

[8] Hamrock B J, Dowson. Ball Bearing Lubrication[M]. New York: John Wiley & Sons, 1981.

[9] 方兵, 张雷, 曲兴田, 等. 角接触球轴承刚度理论计算与实验[J]. 吉林大学学报(工学版), 2012, 42(4): 840-844. Fang Bing, Zhang Lei, Qu Xing-tian, et al. Theoretical Calculation and Experiment of Stiffness of Angular Contact Ball Bearings[J]. Journal of Jilin University, 2012, 42(4): 840-844.

[10] 邢济收, 戴曙. 预紧后角接触球轴承刚度计算[J]. 机床, 1990(5): 8-10.

[11] 王硕桂, 夏源明. 过盈配合量和预紧力对高速角接触球轴承刚度的影响[J]. 中国科学技术大学学报, 2006, 36(12): 1314-1320.Wang Shuo-gui, Xia Yuan-ming. Interference Magnitude and Preload Impact the Stiffness Influence of High Speed Angle Contact Ball Bearing[J]. Journal of University of Science and Technology of China, 2006, 36(12): 1314- 1320.

(责任编辑: 许 妍)

Simulation and Analysis on Radial Stiffness of Angular Contact Ball Bearing

LI Chuan-xi, DUAN Hao, WANG Yun

(Kunming Branch of the 705 Research Institute, China Shipbuilding Industry Corporation, Kunming 650118, China)

Angular contact ball bearing is one of the key components in turbopump launch system, and its radial stiffness is vital for the performance of the turbopump launch system. To obtain reliable radial stiffness of the angular contact bearing, this paper derives a formulas for calculating the radial stiffness according to the Hertz contact theory and the geometrical relationship of the bearing. This formula considers the coupling of axial preload and radial load, the radial clearance, and the interference magnitude. Moreover, the nonlinear influences of different factors on the radial stiffness are analyzed. This study may provide a reference for integral analysis of rotating machine.

turbopump launch system; angular contact ball bearing; radial stiffness

李传喜, 段浩, 王云. 角接触球轴承径向刚度仿真[J]. 水下无人系统学报, 2017, 25(4): 351-358.

TJ635; TH133.3

A

2096-3920(2017)04-0351-08

10.11993/j.issn.2096-3920.2017.04.008

2017-05-17;

2017-06-28.

李传喜(1990-), 男, 在读硕士, 研究方向为水下发射技术.