基于CFD/CSD耦合方法的旋翼气动弹性载荷计算分析

马砾， 招启军， 赵蒙蒙, 王博

南京航空航天大学 直升机旋翼动力学国家级重点实验室， 南京 210016

基于CFD/CSD耦合方法的旋翼气动弹性载荷计算分析

马砾， 招启军*， 赵蒙蒙, 王博

南京航空航天大学 直升机旋翼动力学国家级重点实验室， 南京 210016

为提高直升机前飞状态下旋翼非定常气动弹性载荷的预估精度，在旋翼气动弹性综合分析方法中引入旋翼CFD模块，建立了一套基于 CFD/CSD松耦合分析的计算方法和程序。为高效解决流固耦合方法中由于桨叶挥舞、扭转等弹性变形带来的旋翼贴体网格变形问题，采用基于代数变换方法的网格变形技术，桨叶运动变形量和旋翼气动力信息通过流固交接面传递。旋翼流场分析方法中，主控方程采用耦合S-A湍流模型的Navier-Stokes方程，围绕旋翼流场的网格采用结构嵌套网格方法生成，无黏通量计算采用Roe格式，时间推进采用双时间法。旋翼结构分析中，考虑旋翼配平，基于Hamilton变分原理和20自由度Timoshenko梁模型求解弹性旋翼非线性运动方程。分别对CSD和CFD方法进行验证，在此基础上，计算了SA349/2旋翼桨叶在前飞状态下的非定常气动力、挥舞弯矩、摆振弯矩和扭转力矩，并与飞行测试数据进行了对比。计算表明： CFD/CSD耦合方法可以显著提高旋翼非定常气动弹性载荷的分析精度，精确捕捉桨叶表面压强峰值、激波位置等，表明本文发展的旋翼CFD/CSD耦合方法可以有效地运用到旋翼气动弹性载荷的预测分析中。

旋翼； 气动弹性载荷； CFD/CSD耦合方法； Navier-Stokes方程； 网格变形技术； 前飞状态

旋翼是直升机主要的气动力来源，也是其主要振源之一，准确获取旋翼非定常气动弹性载荷是进行直升机减振优化、强度校核及气弹稳定性研究工作的前提[1]。对旋翼气动弹性载荷的准确预估也是旋翼气动弹性分析领域中最具挑战性的难题之一。一方面，直升机旋翼工作在复杂三维非定常气动环境中，非定常气动载荷特征明显；另一方面，由于直升机旋翼桨叶是细长柔性体，弹性桨叶在旋转过程中同时存在挥舞、摆振、扭转及轴向拉伸等多自由度的弹性变形运动，受非定常气动载荷的影响，这些运动之间存在非线性的耦合关系，从而产生复杂的结构(弹性)载荷，桨叶产生结构变形，继而影响气动力的重新分布。因此，旋翼桨叶的气动载荷和结构运动响应是相互依赖和相互耦合的。要准确预估直升机旋翼桨叶的气动弹性载荷，需要综合空气动力学、结构动力学和数值计算方法等多学科知识，构建合理的旋翼气动弹性综合分析方法[2]。

在早期旋翼气动弹性综合分析中，旋翼气动力的计算通常采用滑流理论、叶素理论等简单模型，导致气动性能计算精度较差，后来的自由尾迹方法虽然可以有效获得旋翼流场的诱导速度分布，提高了旋翼气动特性的计算精度，但在模拟由于黏性引起的流动分离现象及气动阻力时存在局限性。随着计算流体力学(CFD)技术的发展和计算机性能的大幅提高，以考虑黏性影响的Navier-Stokes方程为主控方程的CFD方法为准确分析旋翼流动细节及其气动特性提供了一个新途径。因此，将先进的CFD方法引入旋翼气动弹性综合分析中，构建旋翼CFD/计算结构动力学(CSD)耦合方法，提高旋翼气动弹性载荷的模拟精度已成为当前旋翼气动弹性综合分析领域的最新热点[3]。

在旋翼CFD/CSD耦合分析方面，1986年，Tung和Caradonna等[4]首次提出了旋翼CFD/CSD松耦合迭代方法，该方法得到了广泛认可。2006年，Potsdam等[5]利用松耦合方法将OVERFLOW-D 旋翼CFD求解器和CAMRAD-II旋翼CSD求解器耦合，对UH-60A旋翼在高速、低速、动态失速3种飞行状态下的载荷进行了预估，计算结果表明这种耦合方法对旋翼气动力和力矩有较高的预测精度。2013年，Zhao和He[6]采用基于Lagrange描述的黏性涡粒子(VVPM)与CFD/CSD程序结合，对UH-60A旋翼桨叶结构特性进行了模拟，尽管提高了旋翼在BVI状态下结构载荷的计算精度，但与试验值仍有一定误差。2015年，Lim[7]耦合了基于Navier-Stokes方程的OVERFLOW2软件和CAMRAD-II软件，考虑多段桨尖影响，对旋翼结构特性和气动特性尝试了优化设计并取得了初步结果。

国内在运用CFD/CSD耦合方法进行旋翼气动弹性分析研究方面起步较晚，仍处于发展阶段。2010年，王海[8]尝试进行了基于Euler方程的CFD/CSD耦合分析，并进行了简单的验证。2015年，王俊毅等[9]发展了基于Navier-Stokes方程的直升机前飞状态旋翼气动特性分析的CFD/CSD耦合方法，湍流模型采用了零方程的B-L模型，提高了旋翼气动载荷的预估精度，但针对旋翼弹性载荷及气动性能的研究尚未开展。综上所述，旋翼CFD/CSD分析方法中桨叶弹性变形对旋翼流场和非定常气动弹性载荷带来的影响研究还不够深入，为此需要提高旋翼非定常气动特性及弹性载荷的模拟精度，这对CFD方法的数值离散格式、湍流模型、气动弹性耦合策略和网格变形方法等都提出了很高的要求。

鉴于此，基于先进的CSD和CFD方法，建立了适合前飞非定常状态下直升机旋翼CFD/CSD耦合数值模拟方法。为了准确模拟黏性大分离流动，流场控制方程采用雷诺平均Navier-Stokes(RANS)方程，湍流模型采用一方程的S-A湍流模型，针对耦合过程中由于桨叶弹性变形带来的网格变形问题，发展了一套高效快速的网格变形方法、弹性网格挖洞方法和贡献单元搜索方法。应用所建立的方法，分别对旋翼结构动力学(CSD)模块和刚性旋翼流场分析(CFD)模块进行了验证。采用CFD/CSD耦合方法，通过对不同飞行状态下SA349/2旋翼桨叶的气动载荷、结构载荷以及流场的数值模拟，对前飞状态下弹性桨叶旋翼流场气流分离、激波失速、桨-涡干扰等现象进行了细致分析，揭示了旋翼非定常气动弹性载荷变化特性，得到了有意义的结论。

1 数值方法

1.1 CSD方法

1.1.1 结构动力学计算方法

采用Hamilton变分原理建立旋翼桨叶动力学方程[10]，在非保守力学系统中，从时刻t1到t2的运动中，系统的势能和动能与外力虚功的积分为零，其数学表达式为

(1)

式中：δU、δT和δW分别表示某一时刻桨叶的应变能的变分、动能的变分和外力所做的虚功的变分。

图1 桨叶单元节点自由度排列 Fig.1 Arrangement of degree of freedom of blade element node

将用插值型函数离散得到的相应位移代入变分表达式，可以得到

(2)

式中：q为单元自由度向量；KL和KNL分别为线性和非线性刚度矩阵；M为对称质量矩阵；C为非对称的科氏阻尼矩阵；KCF为离心力刚度矩阵；FCF为离心力向量；KI为分布力矩所导致的刚度型矩阵；FI为外力向量。

采用有限元法对式(2)单元阵进行组装，最后得到整个桨叶的运动方程：

(3)

本文采用改进Newmark-Beta方法[11]，对旋翼桨叶运动方程求解。

1.1.2 桨叶模态分析

为了确定桨叶的频率和振型，必须对桨叶进行固有特性分析，这也是为了验证所建立的桨叶结构数值分析模型能否较为准确地模拟真实旋翼的动力学特性，以便用于桨叶气弹耦合的分析中。模态分析中，假定桨叶不受气动外力的干扰，即认为是真空状态下的模态分析，则动力学方程可简化为

(4)

1.1.3 桨叶网格弹性变形策略

为兼顾计算效率，本文采用高效、高质量的代数变换方法来实现桨叶贴体网格变形[12]。通过CSD方法计算得到桨叶每一个方位角和剖面的弹性位移，便可以得到坐标转换矩阵Tdc和线性变形阵dlin，再针对桨叶网格所有坐标(x,y,z)进行代数变换，通过式(5)计算得到桨叶固连坐标系中的变形网格坐标：

(5)

式中：(xd,yd,zd)为桨叶网格变换后坐标。

图2为SA349/2旋翼桨叶贴体网格变形示意图，其中下方为变形前网格，上方为变形后网格。

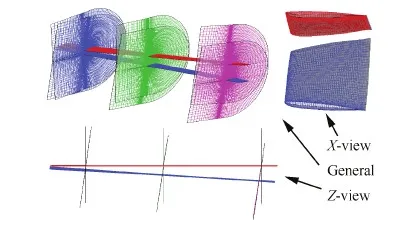
图2 桨叶网格变形示意图Fig.2 Schematic of blade grid deformation

1.2 CFD方法

1.2.1 网格生成方法

旋翼运动复杂，在旋转过程中伴随有挥舞、摆振和周期变距等运动。因此，本文使用了运动嵌套网格方法对旋翼流场进行数值模拟。本文的桨叶贴体网格和背景网格均采用结构网格方法。如图3所示，桨叶贴体结构网格采用C-O型网格。首先，采用求解Poisson方程[13]生成围绕二维翼型剖面的C型网格，为提高黏性计算的精度，采用Higenstock源项修正策略调整网格疏密和正交程度，为了准确捕捉附面层内流动，第1层翼型网格的壁面距离取为5×10-6c(y+≈1)，c为翼型弦长。然后，根据桨叶外形的翼型分布和扭转分布规律，沿展向对C型网格进行插值来获得桨叶段间的网格，桨根和桨尖处网格采用绕翼型中弧线翻折的方法生成。

图3 SA349/2旋翼桨叶网格示意图Fig.3 Schematic of SA349/2 rotor blade grid

前飞计算时，旋翼向前运动，涡向后脱出，则采用了长方体笛卡儿网格。对于不同的计算状态，为准确模拟旋翼桨尖涡的发展轨迹，对包含旋翼尾迹区域进行了加密(见图2)，利于有效计算流场速度空间分布等信息。在本文的旋翼CFD计算中，桨叶贴体网格大小为237×45×61(弦向×法向×展向)，背景网格大小为160×164×152(弦向×法向×展向)。

1.2.2 运动嵌套网格方法

在弹性桨叶流场计算过程中，由于桨叶每个时间步都存在弹性变形，旋翼旋转时的每个方位角都必须进行背景网格洞单元识别和桨叶网格贡献单元搜索。本文采用高效的“扰动衍射”[14]法来快速确定桨叶在背景网格中的洞边界。采用“最小距离方法”[15]进行背景网格人工内边界的贡献单元搜索，进而完成旋翼网格与背景网格之间的流场信息传递。图4给出了本文所采用的运动嵌套网格系统、洞边界单元以及搜索到的贡献单元示意图。

图4 运动嵌套网格系统示意图Fig.4 Schematic of moving-embedded grid system

1.2.3 流场计算方法

为精确模拟旋翼非定常流动特性，捕捉桨叶表面激波位置、流动分离等现象，采用积分形式的RANS方程作为旋翼贴体网格流场求解的控制方程[16]：

(6)

式中：V和S分别为控制体体积和表面积;n为控制体表面法矢；守恒变量、无黏通量和黏性通量分别为

其中：Vr为相对速度；Vt为牵连速度；p为压强；ρ为流体单元密度；E为单元总内能；[u,v,w]为气流速度；H为单元总焓能；τij和θi分别为黏性应力张量项和热通量项，与温度导数相关。

采用S-A[17]湍流模型，其计算量小，对计算复杂流动有很强的鲁棒性，且湍流的涡黏度场是连续的。在旋翼非定常流场计算中，本文采用双时间法进行求解。为了提高流场求解的效率，伪时间推进方法采用LU-SGS隐式格式[18]。首先对控制方程中的时间导数进行离散后得

(7)

式中：m为推进层数；Res为残值；Q=[ρ,u,v,w,p]为原始变量。然后采用LU-SGS隐式格式对式(7)进行求解。

空间离散采用有限体积法，采用Roe格式[19]计算无黏通量，具体为

|ARoe|i+1/2(WR-WL)]

(8)

式中：ARoe为平均雅可比矩阵，该矩阵考虑了近似Riemann问题的波的大小和传播方向，下标i+1/2表示单元交界面；WL和WR分别为交界面左右两侧的守恒量。

1.3 CFD/CSD耦合方法

本文采用松耦合[20-21]方式实现CFD程序与CSD程序的耦合，主要分为2个步骤：① 气动信息向结构计算的传递，主要通过传递CFD计算得到的气动力来实现。CFD程序在计算至少一周期以后获得一周期的升力、阻力和俯仰力矩，再代入结构计算程序(CSD)进行计算。② CFD气动计算中计入桨叶弹性变形作用，需要对网格进行弹性变形，由于CFD计算采用时间推进求解，因而需要在每步计算前对当前站点上的网格进行变形。本文松耦合计算的流程如图5所示。

步骤1分别对旋翼CFD模块和CSD模块进行初始化。

步骤2对采用基于简单升力线模型的旋翼CSD程序进行计算，得到操纵量以及一个桨叶旋转周期上每个方位角收敛的桨叶弹性轴处的变形量(位移和扭转角)。

步骤3将一个周期的桨叶弹性变形量导入网格变形模块，并完成桨叶贴体网格变形。

步骤4将变形后的桨叶贴体网格代入流场CFD程序，进行下一个周期的时间推进计算。

步骤5将一个周期桨叶(表面网格)上的非定常气动力和力矩通过插值传递到桨叶结构结点上，进行下一个周期的配平和桨叶结构响应(CSD)计算。

步骤6重复步骤2～步骤5的过程，直到旋翼配平量、桨叶结构响应和气动载荷收敛为止，输出流场及结构载荷等结果。

图5 旋翼配平及气动弹性耦合流程图Fig.5 Flowchart of rotor trim and aeroelastic coupling

2 模型验证

2.1 CSD模型验证

为验证本文发展的旋翼CSD方法的有效性，对文献[10]给出的样例旋翼模型进行验证。图6给出了本文计算得到的旋翼共振图。图中：1F、1L和1T分别表示一阶挥舞、一阶摆振和一阶扭转模态；Ω为转速。可以看出，CSD模块可以准确地计算旋翼桨叶的固有特性，各阶频率与试验值符合得都较好。

图7为模型旋翼在前进比μ为0.3时的响应分析与文献[10]计算比。图中：φ为方位角。可以看出，本文发展的旋翼CSD方法可以有效地计算前飞状态下旋翼的气动弹性响应，表明旋翼CSD模块为CFD/CSD耦合计算提供了一个良好的动力学分析模型。

图6 模型旋翼桨叶共振Fig.6 Resonance of model rotor blade

图7 前飞状态旋翼不同方位角桨尖响应Fig.7 Response of blade-tip with different azimuth angles in forward flight

2.2 CFD模型验证

本文计算了前飞无升力状态下刚性Caradonna-Tung旋翼[22]的桨叶表面压强系数Cp来验证旋翼CFD模型的有效性，计算状态参数为：前进比为0.2，桨尖马赫数为0.8。计算结果和试验值的对比如图8所示，R为旋翼半径。可见，计算结果与试验值吻合较好，表明本文的旋翼非定常流场计算方法能够有效地用于CFD/CSD耦合分析中的流场计算部分。

图8 前飞状态Caradonna-Tung旋翼桨叶表面的压强系数分布Fig.8 Distribution of pressure coefficient on blade surface of Caradonna-Tung rotor in forward flight

3 旋翼气动弹性载荷分析

3.1 旋翼桨叶模态分析

分别采用刚性旋翼CFD方法、自由尾迹方法[23]和CFD/CSD耦合方法对旋翼进行气动弹性载荷和旋翼流场分析。采用具有详细结构参数的SA349/2旋翼[24]作为验证算例。SA349/2旋翼基本参数如表1所示，其中的结构参数为UMARC的输入值。

表2为本文计算得到的SA349/2旋翼固有频率和CAMRAD软件[23]计算结果的对比。可以看出，2种方法吻合较好。

图9为本文计算得到的SA349/2旋翼共振与CAMRAD软件计算结果对比。可以看出，桨叶的固有频率随着转速的增大而增加，在工作转速下桨叶固有频率与CAMRAD软件计算值吻合较好。

表1 SA349/2旋翼基本参数[24]Table 1 Basic parameters of SA349/2 rotor[24]

表2SA349/2旋翼固有频率计算结果

Table2CalculationresultsofnaturalfrequencyofSA349/2rotor

ModeNaturalfrequency/HzCAMRAD[23]CalculatedRelativeerror/%1L0．590．58131．471F1．021．02110．1082F2．782．77580．151T4．164．17170．281

图9 SA349/2旋翼桨叶共振Fig.9 Resonance of SA349/2 rotor blade

图10为SA349/2旋翼桨叶的振型图，r为剖面沿桨叶展向位置；R为桨叶半径。可以看出，本文采用的CSD模型可以有效捕捉弹性旋翼桨叶的模态。

表3给出了本文计算的高速和低速2种不同飞行状态时的参数。表中：CT为旋翼拉力系数，σ为旋翼实度。

图10 SA349/2旋翼桨叶振型Fig.10 Vibration model of SA349/2 rotor blade

表3 SA349/2旋翼飞行试验状态基本参数Table 3 Basic parameters of SA349/2 rotor flight test

3.2 高速前飞状态桨叶气动弹性载荷及流场分析

采用CFD/CSD松耦合方法对高速飞行状态下的弹性SA349/2旋翼桨叶进行了载荷预测，并与文献[23]中的试验值进行对比。飞行状态1：前进比为0.378，CT/σ=0.071。图11为采用不同方法计算的在0.97R位置桨叶剖面压强分布和试验值的对比。可以看出，相比于传统刚性旋翼CFD方法，采用计入桨叶弹性变形的CFD/CSD耦合方法可以更加精确地捕捉桨叶表面压力峰值以及激波位置和强度，其中在150°方位角，由于流场计算中计入了旋翼在气动载荷作用下的弹性变形影响，桨叶表面未产生气流分离和激波，桨叶剖面压强分布得到缓和，这与试验值相一致，而在该方位角下刚性CFD计算结果仍有激波出现。

图11 飞行状态1下SA349/2旋翼桨叶表面的压强系数分布Fig.11 Distribution of pressure coefficient on blade surface of SA349/2 rotor in Case 1

图12为计算获得的SA349/2旋翼不同桨叶剖面的等效法向力系数Cn与试验值、刚性CFD以及自由尾迹方法计算结果的对比。图12(c)中4个小图是对应大图不同位置的剖面压强系数。可见，采用CFD/CSD耦合方法的旋翼气动载荷预测总体更贴合试验数据，由于引入CSD桨叶变形模块，扭转力矩对桨叶产生了一定的弹性变形，改变了桨叶剖面的气动分布，与实际情况相符，升力的幅值和相位相对于刚性CFD与试验值更加吻合，说明本文旋翼CFD/CSD耦合方法可以有效地预测直升机旋翼气动载荷，为结构载荷的预测提供一个较准确的外部载荷输入。

图13给出了旋翼桨叶剖面法向力系数在桨盘平面内的分布情况。可以看出，在桨叶前行侧，由于桨叶剖面相对来流速度较大，法向力系数相对较大的区域集中在桨尖区域，而在270° 后行桨叶一侧，靠近桨叶旋转中心处转速小于μΩR的一段桨叶上，桨叶剖面相对气流周向分量自翼型后缘吹向前缘，从而出现“反流区”，导致法向力出现负值。

图14给出了CFD/CSD耦合方法计算得到的不同方位角桨叶上表面压强分布，p为无量纲的桨叶表面压强大小。可以看出，在旋翼前行侧，由于桨叶的桨尖区域处于跨声速区，该区域将有激波产生，从而出现气流分离现象，导致压强梯度沿桨叶弦向较大，而后行桨叶桨尖区域表面展向流动比重较大，压强梯度沿桨叶弦向得到缓和。

图15给出了CFD/CSD耦合方法计算得到的旋翼桨叶在各个方位角处的表面流线及90° 方位角时桨尖附近表面流动细节。可以看出，旋翼后行桨叶沿展向的三维流动现象非常明显，而在桨叶前行侧，桨叶表面展向流动明显弱于旋翼后行侧。由于计算状态的前进比较大，属于高速前飞状态，在30°～90° 方位角处，桨尖附近会有气流分离现象出现，前行桨叶处于跨声速区，因而在该区域会有激波产生，这与图11计算的桨叶剖面压强分布规律相对应。

图12 飞行状态1下桨叶不同剖面法向力系数分布Fig.12 Distribution of normal force coefficient of blade on different cross-sections in Case 1

图13 法向力系数沿桨盘分布Fig.13 Distribution of normal force coefficient in the plane disk

图14 桨叶不同方位角上表面压强分布 Fig.14 Distribution of surface pressure of blade at different azimuth angles

图16给出了前进比为0.378时CFD/CSD耦合方法计算得到SA349/2旋翼桨叶展向不同剖面的非定常挥舞弯矩系数CFM与试验值及自由尾迹方法计算结果的对比。可以看出，挥舞弯矩相位与幅值捕捉较好，在高速前飞状态，桨叶的挥舞结构载荷在90°～220° 方位角内较小，但是在30° 附近和270° 附近载荷峰值得到了加强。

图17给出了非定常摆振弯矩系数CIM的计算结果对比。可以看出，摆振弯矩幅值基本一致，但是在桨叶后行侧相位捕捉有一定偏差，可能与缺少摆振阻尼器的模拟有关。

图18给出了扭转力矩系数CTM的计算结果对比。扭转力矩与试验值吻合较好，高速状态下，扭转载荷高频响应成分微弱，整体趋势较为平缓，90° 方位角附近出现抬头力矩峰值，而在180° 方位角附近出现低头力矩峰值。

图15 桨叶在不同方位角处的表面流线Fig.15 Surface streamlines of blade at different azimuth angles

图16 飞行状态1下挥舞弯矩系数对比Fig.16 Comparison of flap bending moment coefficient in Case 1

图17 飞行状态1下摆振弯矩系数对比Fig.17 Comparison of lag bending moment coefficient in Case 1

图18 飞行状态1下扭转力矩系数对比Fig.18 Comparison of torsion moment coefficient in Case 1

3.3 低速前飞状态桨叶气动弹性载荷分析验证

飞行状态2：前进比为0.140，CT/σ=0.065。图19为CFD/CSD耦合方法计算的旋翼桨叶气动载荷，并与文献[23]中的试验值、刚性CFD方法以及自由尾迹方法结果进行对比。可见，CFD/CSD耦合方法和刚性CFD方法在一定程度上都能较好地反映旋翼非定常气动载荷变化，而自由尾迹方法在低速状态下计算结果和试验结果在幅值和相位上都存在一定差距。由于前进比较低，该飞行状态下，旋翼桨-涡干扰严重，气动载荷的非定常效应较飞行状态1的高速前飞更加明显，在图19(b)和图19(c)中，测试剖面靠近桨尖，90° 和270° 处气动载荷振荡剧烈，相对于刚性CFD方法，本文发展的旋翼CFD/CSD耦合方法在预测桨-涡干扰时的气动载荷幅值方面更加精确。

图19 飞行状态2下桨叶不同剖面法向力系数分布Fig.19 Distribution of normal force coefficient of blade on different cross-sections in Case 2

图20 飞行状态2下挥舞弯矩系数对比Fig.20 Comparison of flap bending moment coefficient in Case 2

图20为飞行状态2下的桨叶剖面挥舞弯矩系数CFD/CSD耦合方法与试验结果及自由尾迹方法对比。CSD/CFD耦合方法计算得到的挥舞弯矩整体分布与试验值的对比呈现一致的变化趋势，从图20中可以看出，在270° 方位角处出现了一个明显的载荷峰值，这主要由于桨-涡干扰造成的冲量作用使桨尖处气动力载荷达峰值而引起的结果，而自由尾迹方法由于低速状态下非定常气动力计算存在一定误差，导致计算得到的非定常挥舞弯矩与试验值相比误差较大。

4 结 论

基于Navier-Stokes方程、弹性桨叶运动嵌套网格方法、网格变形方法和Hamilton变分原理，建立了一套用于旋翼非定常气动特性和气动弹性载荷分析的旋翼CFD/CSD松耦合方法，并进行了较系统的算例验证。

1) 流固耦合策略及桨叶弹性网格变形方法能够有效地进行CFD与CSD模块的气动力和弹性变形之间的信息交换。

2) 相比于刚性旋翼CFD方法，旋翼CFD/CSD耦合方法在高速前飞状态计算得到的桨尖区域桨叶剖面的压强分布相比于刚性桨叶明显改善，可以更准确地捕捉桨叶剖面压力峰值以及激波位置和强度，与实际情况相符；在低速前飞状态，可以更加准确地模拟由于桨-涡干扰引起的气动载荷非定常效应。

3) 相比于传统气弹耦合方法中的自由尾迹模型，旋翼CFD/CSD耦合方法可以更加准确地捕捉挥舞弯矩、摆振弯矩和扭转力矩的相位和幅值，结果反映气动载荷的精度对结构载荷的计算有重要意义。

相比于刚性旋翼CFD方法和自由尾迹方法，CFD/CSD耦合方法普遍适用于直升机高速前飞状态和低速前飞状态的气动弹性载荷预估，为旋翼气动弹性综合分析中的减振优化、强度校核及气动弹性稳定性研究工作提供基础。

[1] CONLISK A T. Modern helicopter rotor aerodynamics[J]. Progress in Aerospace Science, 2001, 37(5): 419-476.

[2] DATTA A. Fundamental understanding, prediction and validation of rotor vibratory loads in steady-level flight[D]. Park: University of Maryland, 2004.

[3] DATTA A, CHOPRA I. Prediction of the UH-60A main rotor structural loads using computational fluid dynamics/comprehensive analysis coupling[J]. Journal of the American Helicopter Society, 2008, 53(4): 351-365.

[4] TUNG C, CARADONNA F X, JOHNSON W. The prediction of transonic flows on an advancing rotor[J]. Journal of the American Helicopter Society, 1986, 32(7): 4-9.

[5] POTSDAM M, YEO H, JOHNSON W. Rotor airloads prediction using loose aerodynamic/structural coupling[J]. Journal of Aircraft, 2006, 43(3): 732-742.

[6] ZHAO J G, HE C J. Rotor blade structural loads analysis using coupled CSD/CFD/VVPM [C]//Proceedings of the 69th Annual Forum of the American Helicopter Society, Phoenix, 2013： 1452-1468.

[7] LIM J W. Consideration of structural constraints in passive rotor blade design for improved performance[J]. Aeronautical Journal, 2015, 119(1222): 1513-1539.

[8] 王海. 计入桨叶结构弹性的新型桨尖旋翼流场数值模拟研究[D]. 南京: 南京航空航天大学, 2010.

WANG H. Numerical simulation for the flowfield of new-tip rotors with effect of blade elasticity[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010 (in Chinese).

[9] 王俊毅, 招启军, 马砾. 直升机旋翼桨-涡干扰状态非定常气弹载荷高精度预估[J]. 航空动力学报, 2015, 30(5): 1267-1274.

WANG J Y, ZHAO Q J, MA L. High-precision prediction on unsteady aeroelastic loads of helicopter rotors in BVI condition[J]. Journal of Aerospace Power, 2015, 30(5): 1267-1274 (in Chinese).

[10] YUAN K, FRIEDMANN P. Aeroelasticity and structural optimization of composite helicopter rotor blades with swept tips:NASA CR-4665[R]. Washington, D.C.: NASA, 1995.

[11] YAMAKAWA H, OHNISHI T. Dynamic response analysis with many degrees of freedom using step-by-step transfer matrix method[J]. Transactions of the Japan Society of Mechanical Engineers C, 1982, 48(429): 672-681.

[12] DATTA A, SITARMAN J, CHOPRA I, et al. CFD/CSD prediction of rotor vibratory loads in high-speed flight[J]. Journal of Aircraft, 2006, 43(6): 1698-1709.

[13] HSU K, LEE S L. A numerical technique for two-dimensional grid generation with grid control at all of the boundaries[J]. Journal of Computational Physics, 1991, 96(2): 451-469.

[14] 赵国庆, 招启军, 吴琪. 旋翼非定常气动特性CFD模拟的通用运动嵌套网格方法[J]. 航空动力学报, 2015, 30(3): 546-554.

ZHAO G Q, ZHAO Q J, WU Q. A universal moving-embedded grid method for CFD simulation of unsteady aerodynamic characteristics of rotor[J]. Journal of Aerospace Power, 2015, 30(3): 546-554 (in Chinese).

[15] 赵国庆, 招启军, 王清. 旋翼翼型非定常动态失速特性的CFD 模拟及参数分析[J]. 空气动力学学报, 2015, 33(1): 72-81.

ZHAO G Q, ZHAO Q J, WANG Q. Simulations and parametric analyses on unsteady dynamic stall characteristics of rotor airfoil based on CFD method[J]. Acta Aerodynamica Sinica, 2015, 33(1): 72-81 (in Chinese).

[16] BLAZEK J. Computational fluid dynamics: Principles and applications, second edition[M]. Amsterdam: Elsevier, 2005: 16-18.

[17] SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows: AIAA-1991-0439[R]. Reston: AIAA, 1991.

[18] LUO H, BAUM J D, LOHNER R. A fast, matrix-free implicit method for compressible flows on unstructured grids[J]. Journal of Computational Physics, 1998, 146(2): 664-690.

[19] ROE P L. Approximate Riemann solvers, parameter vectors and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.

[20] JOHNSON W. Milestones in rotorcraft aeromechanics: NASA/TP-2011-215971[R]. Washington, D.C.: NASA, 2011.

[21] POTSDAM M, YEO H, JOHNSON W. Rotor airloads prediction using loose aerodynamic/structural coupling[J]. Journal of Aircraft, 2006, 43(5): 732-742.

[22] CARADONNA F X, LAUB G H, TUNG C. An experimental investigation of the parallel blade-vortex interaction: NASA TM-86005[R]. Washington, D.C.: NASA, 1984.

[23] 赵景根, 徐国华, 招启军. 基于自由尾迹分析的直升机旋翼下洗流场计算方法[J]. 兵工学报, 2006, 27(1): 63-68.

ZHAO J G, XU G H, ZHAO Q J. A calculating method of helicopter rotor downwash flowfield based on free wake analysis[J]. Acta Armamentarii, 2006, 27(1): 63-68 (in Chinese).

[24] HEFFERMAN R M, GAUBERT M. Structural and aerodynamic loads and performance measurements of an SA349/2 helicopter with an advanced geometry rotor: NASA TM-88370[R]. Washington, D.C.: NASA,1986.

(责任编辑： 鲍亚平)

Computation analyses of aeroelastic loads of rotor based onCFD/CSD coupling method

MALi,ZHAOQijun*,ZHAOMengmeng,WANGBo

NationalKeyLaboratoryofScienceandTechnologyonRotorcraftAeromechanics,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China

In order to improve the prediction accuracy of the unsteady aeroelastic load of the rotor in forward flight of the helicopter, the rotor CFD module is introduced into the comprehensive analysis method for rotor aeroelastic, and then an analytical model and corresponding code based on CFD/CSD loose coupling method are established. In order to solve the deformation problem of blade body-fitted grid caused by aeroelastic deflections such as flapping and torsional motion in rotor CFD/CSD coupling process, the blade grids are deformed using algebraic method, and blade motion deformation and rotor aerodynamic force information are transferred through the interface between fluid and solid. In the analysis method for rotor flowfield, the Navier-Stokes equations coupled with S-A turbulence model are used as governing equations, and then the rotor moving-embedded grids are constructed. The Roe scheme is employed in spatial discretization, and a dual-time algorithm is adopted for temporal discretization. In the analysis of the rotor structure, considering the rotor trim, the nonlinear equations for motion of elastic rotor are solved based on Hamilton variational principle and 20 degree of freedom Timoshenko beam model. The CSD and CFD methods are validated . Based on aforementioned work, the aeroelastic loads on the SA349/2 rotor blade, mainly including unsteady aerodynamic loads and moment in flapping, lagging and torsion direction, are calculated and compared with flight test data. Comparisons of the CFD/CSD calculated results with flight test data demonstrate that the CFD/CSD coupling method has high accuracy in calculating the rotor unsteady aerodynamic load and structural load, and can capture the peak of pressure and shock position accurately. The method proposed could be effectively applied to prediction analysis of the aeroelastic loads of the rotor.

rotor; aeroelastic load; CFD/CSD coupling method; Navier-Stokes equations; grid deformation technology; forward flight

2016-09-08;Revised2016-10-06;Accepted2016-11-09;Publishedonline2016-11-280922

URL：www.cnki.net/kcms/detail/11.1929.V.20161128.0922.002.html

s：NationalNaturalScienceFoundationofChina(11572156);AProjectFundedbythePriorityAcademicProgramDevelopmentofJiangsuHigherEducationInstitutions

2016-09-08；退修日期2016-10-06；录用日期2016-11-09； < class="emphasis_bold">网络出版时间

时间：2016-11-280922

www.cnki.net/kcms/detail/11.1929.V.20161128.0922.002.html

国家自然科学基金 (11572156)； 江苏省高校优势学科建设工程资助项目

*

.E-mailzhaoqijun@nuaa.edu.cn

马砾， 招启军， 赵蒙蒙, 等． 基于CFD/CSD耦合方法的旋翼气动弹性载荷计算分析J． 航空学报,2017,38(6):120762.MAL，ZHAOQJ,ZHAOMM,etal.ComputationanalysesofaeroelasticloadsofrotorbasedonCFD/CSDcouplingmethodJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):120762.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0292

V211.47

A

1000-6893(2017)06-120762-14

*Correspondingauthor.E-mailzhaoqijun@nuaa.edu.cn