曲外锥乘波体进气道实用构型设计和性能分析

贺旭照， 乐嘉陵

中国空气动力研究与发展中心 超高速空气动力学研究所/高超声速冲压发动机技术重点实验室，绵阳 621000

曲外锥乘波体进气道实用构型设计和性能分析

贺旭照*， 乐嘉陵

中国空气动力研究与发展中心 超高速空气动力学研究所/高超声速冲压发动机技术重点实验室，绵阳 621000

介绍了新型曲外锥乘波前体进气道(CCWI)的一体化设计方法，设计了理论构型并验证了设计方法。在几何参数约束下，获得了隔离段矩形出口，考虑前缘钝度及展向切除的乘波前体进气道构型。基于验证的数值仿真工具及计算网格策略，分析了几何切除及钝度和黏性对一体化构型性能的影响。在来流马赫数为4.0和6.0，迎角(AoA)在-4°～8° 范围内，对设计的乘波前体进气道的基本性能进行了雷诺平均Navier-Stokes数值仿真，结果表明，该乘波前体进气道具有较高的流量捕获和总压恢复特性，隔离段出口参数满足超燃冲压发动机入口需求。该新型乘波前体进气道一体化方案及研究结果为一体化曲外锥乘波飞行器及一体化乘波推进流道的研究奠定了技术基础。

乘波体； 进气道； 一体化； 实用化设计； 试验验证； 数值仿真

吸气式高超声速飞行器的推阻特性，还存在进一步提升优化的紧迫需求[1]。飞行器的升阻比是随飞行马赫数的增加而降低的[2]。同时发动机的比冲随飞行马赫数增加而减小[3]；在一般情况下，发动机捕获流量随飞行速度和高度的增加而减小。综合的结果是飞行器阻力增加，而发动机的推力减小。

从空气动力学的角度看，解决推阻问题，就要增加飞行器的升阻比和提高发动机的流量捕获性能。乘波构型是高升阻比飞行器的最佳选择，但基于现有乘波体设计方法获得的飞行器外形，存在较低的容积率、弯曲的异型结构及不易调节的气流压缩能力等缺陷[4]。

在高超声速条件下可以设计出具有优良性能的进气道[5-7]，如高的总压恢复能力和较高的流量捕获能力、较好的流动均匀性等。但进气道本身的设计并未充分考虑与飞行器前体的流动参数及几何外形的一体化。乘波构型的异型曲面结构，增大了进气道和乘波体的匹配难度，而采用人工修型的方法，会破坏乘波体以及进气道自身的流场结构，会带来附加的升阻比及进气性能损失，使得乘波体和进气道集成于飞行器前体后，很难达到单独设计的指标[8]。

在高超声速飞行器一体化设计方面，Mary和Mark[9]采用锥导乘波体，在锥形流场中流线追踪出进气道的唇罩，而进气道近似采用二维构型几何变换获得。Takashima和Lewis[10]、O’Brien和Mark[11]采用密切锥方法[12]生成前体，前体对称面部分有相对平缓的区域，通过贴合二维进气道的方法完成乘波体和进气道的耦合。Ryan和Mark[13]采用变楔角法生成乘波前体，在前体对称面附近设计了同样的平缓区域，贴合二维进气道与乘波体耦合。You[14]和Li[15]等主要是沿着展向采用密切内锥/外锥的方法获得一体化的前体进气道。现有的研究多停留在概念设计阶段，缺少详细的流动结构及参数的分析研究，以确认设计方法的可行性。同时一体化前体进气道在宽范围内的流动压缩特性，也应重点关注。设计的新型构型必须具有高容积特性和良好的结构可实现性。

笔者前期构建了一套密切曲面内锥乘波前体进气道(Osculating Inward turning Cone Wareriderforebody Inlet, OICWI)设计方法[16-17]，并完成了仿真和试验研究[17-18]。基于内锥的一体化前体进气道，流动压缩性能优良，但在装载容积和结构实现方面，存在进一步提升的空间。

本文介绍了新型曲外锥乘波前体进气道(Curved Cone Waverider forebody Inlet, CCWI)的一体化设计方法，设计了理论构型并完成了设计方法考核。在几何参数约束下，获得了考虑前缘钝度及展向宽度约束的实用化乘波前体进气道构型。基于验证的数值仿真及计算网格策略，分析了展向几何截断及钝度、黏性对一体化构型性能的影响，并在马赫数为4.0和6.0，迎角在-4°～8° 范围内，对设计的实用化乘波前体进气道的基本性能进行了黏性湍流数值仿真，获得了一体化构型的基本压缩性能。目前的研究工作为基于该新型乘波前体进气道的深入研究奠定了基础。

1 轴对称基准流场设计

设计曲外锥乘波前体进气道之前，先要获得外压和内压匹配的轴对称基准流场。轴对称基准流场的结构如图1所示。基准流场中包含了直锥压缩区A′HE、等熵压缩区HKE、型面过渡区KIE、唇罩激波反射区IEJ及激波消除内通道区域IJFG。

A′HE段为直锥流动区域，采用Taylor-Maccoll方程[19]求解该区域的流动参数。HKE为等熵压缩段，是采用特征线方法及流量匹配原理设计的[19-20]。KI是一条和HK相切于K点的三次曲线，该区域的流场参数由特征线EK上的流动参数及物面型线KI确定。IEJ为反射激波区域。设定唇罩型线EJ后，以过渡区域KIE的流场参数作为上游非均匀来流值，通过差值迭代求解反射激波的特征线过程[19-20]，获得激波区域IEJ的流场参数。对于激波消除内通道区域IJFG，基于IG型线及其上的马赫数分布，结合特征线JI上的流动参数及其上的流量，采用流量匹配特征线过程[19-20]，就可获得进气道内通道的上型面JF及消除激波内通道区域IJFG的流场。

本文给出的设计实例，是来流马赫数(Ma∞)为5.5，G点马赫数为3.4，初始直锥角为10°，唇口角为0° 的轴对称流场。基准流场的总收缩比为4.6，内收缩比为1.59。图2上半部分为特征线(Method of Characteristics, MOC)设计获得的基准流场的马赫数Ma云图，下半部分为设计状态下的基准流场的无黏数值仿真结果。数值模拟和特征线设计的流场马赫数分布一致，各流动压缩区域的波系结构相互吻合且和预期一致。内通道的马赫数分布均匀，无反射激波，出口马赫数在3.4左右，压缩系统的无黏总压恢复系数为0.75。图2中Rc为基准流场唇口处半径，x和y分别为轴向和法向坐标。

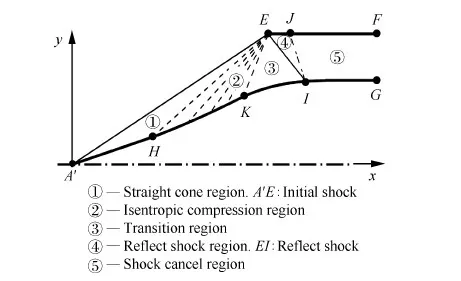
图1 轴对称基准流场结构示意图Fig.1 Schematic map of axisymmetric basic flow filed

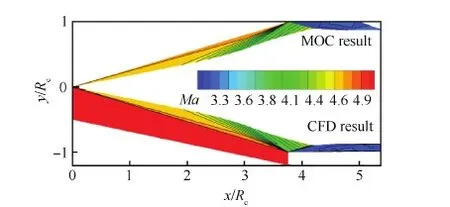
图2 特征线设计和CFD数值仿真结果的轴对称基准流场马赫数云图对比Fig.2 Comparison of Mach number contour of axisymmetric basic flow field of MOC design and CFD numerical simulation results

2 乘波前体进气道的一体化设计方法

2.1 理论构型的设计

密切曲外锥乘波前体进气道的设计，采用了一体化流线追踪和密切轴对称技术，是密切曲外锥乘波体[21]设计方法的进一步发展。图3为设计方法示意图。如图3(a)所示，在前体进气道的唇口平面，定义进气道唇口型线(Inlet Capture Curve, ICC)和乘波体前缘捕获型线(Front Capture Tube, FCT)。ICC和FCT型线的定义见文献[21]。

图3中，在ICC曲线上任一点，如E点，找到其曲率中心A点。通过AE可以构造一个密切面。密切面为垂直纸面的平面，其在前体进气道唇口截面上的投影为AE。密切方法假定密切面就是轴对称基准流场的轴对称面，将基准轴对称流场进行缩放，使得点A和对称轴重合，点E和轴对称流场唇罩初始点重合，这样就可以建立起密切面内对应点和基准轴对称流场的关系。

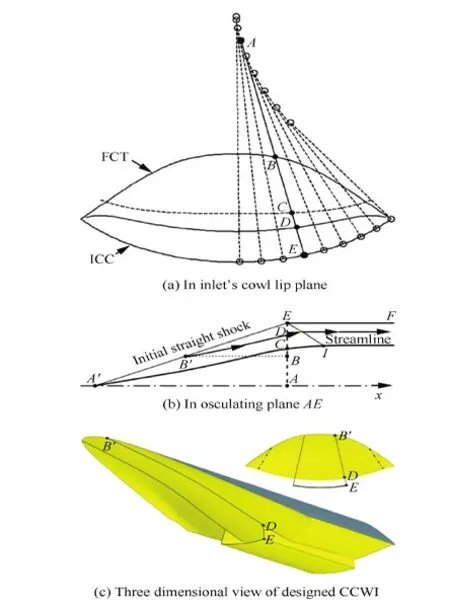
图3 曲外锥乘波前体进气道设计方法示意图Fig.3 Schematic map of CCWI design method

在密切面内，获得乘波前体进气道机体侧和唇罩侧型线的方法如图3(b)所示。密切面在进气道唇口截面上的投影线AE和FCT相交于B点；B点沿基准流场轴向向前延伸，与基准流场的前缘激波A′E相交于B′；始于B′，沿基准流场的流向从头到尾追踪一条流线；把图3(b)中的这条流线，按照示意图中对应点的关系，变换到图3(a)中，就获得了乘波前体进气道在密切面AE内的一条机体侧压缩型线。把图3(b)中的唇罩型线EF，按照相同的对应点关系，变换到密切面AE内，就获得了乘波前体进气道在AE平面内的一条唇罩型线。密切面AE内的2条压缩型线在三维空间中的形状关系，标识于图3(c)中。

沿着ICC逐点重复以上步骤，就可以获得乘波前体进气道机体侧及唇罩侧的整个三维压缩面。在实际应用中，根据流量捕获的需求，只用ICC中部区域的型线，生成进气道的唇罩型面。进气道内通道的侧壁采用位于同一密切面内的唇罩型线和机体侧压缩型线构成。图3(c)给出了生成的一体化密切曲外锥乘波前体进气道的三维视图，图中标识出了密切面AE内对应点，在三维视图中的位置。前体进气道的捕获面如图3(c)中的黑实线所示，其中黄色曲面为前体进气道的机体侧、唇罩侧及内通道侧壁压缩面，灰色曲面为前体进气道的上表面，暂由自由流面生成。所生成的一体化前体进气道构型，乘波前体和进气道自然一体化成型，整体构型流畅饱满，整个压缩面都由流面构成，压缩符合气动原理。目前设计的这款前体进气道理论构型，总收缩比为4.6，内收缩比为1.57。

2.2 理论设计结果对比分析

对设计的前体进气道理论构型，在设计状态Ma∞为5.5，迎角(AoA)为0°，开展了无黏数值仿真，并同设计结果进行了对比。数值仿真工具见3.1节介绍。计算网格有1 081万个，共23个物理块。表1 为内通道出口流动参数(质量加权马赫数Mamw、总压恢复pt、压升比p/p∞和流量系数φ)和设计结果的比较。

图4给出了计算获得的理论构型的流场结构示意图，图中L为前体前缘至进气道内通道出口的长度。图4(a)为等x截面上的马赫数等值线和壁面压力云图。前体激波紧密附着在乘波体侧缘上，高压区域封闭在了乘波体的压缩面内；进气道唇口和三维前体激波完全贴合，实现了三维激波封口的设计预期。图4(b)为前体进气道对称面上的马赫数和压力等值线云图，其流场结构和图2中的基准流场完全相似，唇口反射激波在机体侧无反射。图4(c)为内压缩段出口截面上的马赫数和压力云图，马赫数和压升数值分别在3.4 和10.0左右，均匀性好，且同基准流场出口参数相同。仿真和设计结果的一致性表明，提出的曲外锥乘波体进气道的一体化设计方法，理论上正确，具体设计过程可靠，是一种精确可靠的乘波前体进气道的一体化设计方法。

表1设计和无黏仿真内通道出口参数比较

Table1Parametercomparisonofdesignandinviscidsimulationresultsatexitofinnerinlet

ItemMamwptp/p∞ϕDesign3．4000．75010．301．000Finegrid3．4010．75210．320．996

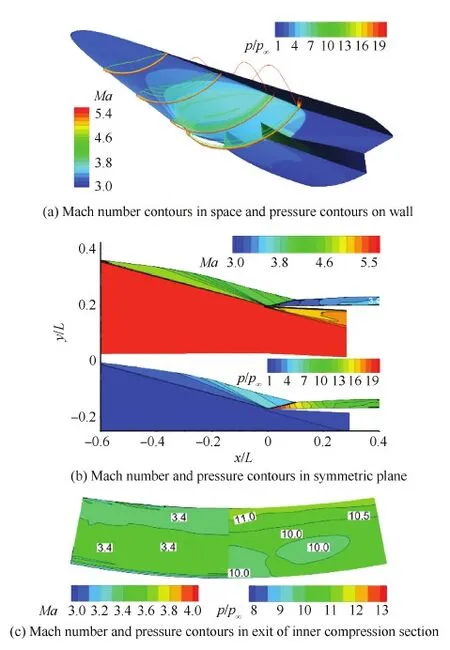
图4 设计状态曲外锥乘波前体进气道流场结构图 Fig.4 Flow field structures of prototype CCWI at design condition

2.3 实用化构型设计

本文所谓“实用化”的内涵，是指对图3(c)的理论构型进行了乘波前体侧缘及内通道侧缘的几何切除；始于异形喉道截面，设计了异形转矩形隔离段及对尖锐前缘做了钝化处理。对理论构型的乘波前体沿着图3(c)中位于密切面内的黑色虚线进行了切除。为了增强进气道的自启动特性，同时又不影响启动状态的流量捕获特性，从唇口前缘出发的69° 线(此线和马赫数为3.5时的唇口反射激波重合)，切除了部分内通道的侧壁，如图5所示。

由于理论构型的喉道截面，是类扇环的异形，从喉道开始，对内通道沿等x截面，进行了异形转矩形的几何形变[22]。如图5(a)所示，图中蓝色曲线为喉道截面型线，黑色矩形为隔离段出口截面型线。变换过程中，原始截面和变换后生成的截面的面心和面积都保持不变。最终获得的隔离段长120 mm，约为7倍的喉道对称面高度，隔离段出口的宽高比为5.2。对前体前缘和唇罩前缘分别做了0.5 mm和0.25 mm的钝度处理。最终获得的使用构型总长607.5 mm，捕获面积7 000 mm2。几何内外收缩比和原始理论构型一致。实用化构型的三维视图如图5(b)所示。

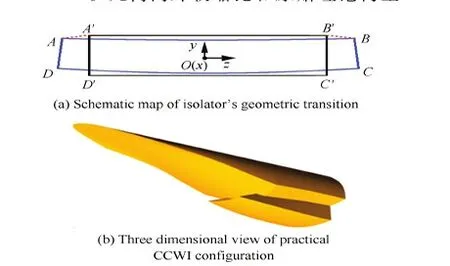
图5 隔离段几何变换及实用化CCWI构型三维视图Fig.5 Schematic map of isolator’s geometric transition and three dimensional view of practical CCWI configuration

3 性能仿真和分析

3.1 数值仿真验证

数值模拟采用了CFD软件AHL3D，AHL3D是内部开发的一款高超声速流动计算软件，具有好的可靠性[23]。为了验证数值工具和网格划分策略的可靠性，开展了计算试验对比研究。试验是在气动中心0.6 m三声速风洞中进行的[24]。采用PSI9016-9116型号压力测量系统测量进气道内壁面沿程静压，测压精度为满量程的0.05%。有关试验研究的详细结果将另文报道。图6为试验模型的风洞照片和测压点的位置分布图。

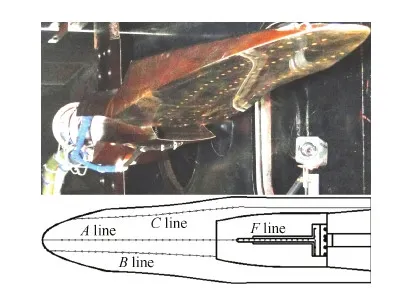
图6 风洞试验模型照片和测点位置示意图Fig.6 Photo of wind tunnel test model and pressure taps position

针对试验来流马赫数为4.03，总压p0=0.63 MPa，总温T0=288 K，迎角为0° 开展了计算试验的对比研究。计算雷诺数同试验值，为3.09×107/m。采用108块结构网格，网格数约4 100万，壁面第一层网格间距为1 μm，内通道流向网格分布301个。无黏通量构建格式是AUSMPW+(Advection Upstream Splitting Method by Pressure Weighted)，MUSCL(Monotone Upstream-centred Schemes for Conservation Law)插值方法用于重构网格面上的物理量。采用了两方程剪切应力输运(SST)湍流模型和壁面函数边界条件[23]。图7为该状态下，计算和试验获得的表面压力数据的对比。从压力分布趋势看，在外压缩部分，经头激波及曲面前体压缩后，壁面压力逐渐上升；在内通道前，型面略有膨胀以减小内通道的气流方向角，此时的壁面压力呈降低趋势；在进入内通道后，进气道上下对称面的压力在经过唇罩三维斜激波压缩后迅速上升，然后在隔离段内出现明显斜激波串。从对比结果看，外压缩区域的计算和试验结果完全一致；在内通道，由于存在复杂的三维斜激波反射及激波边界层干扰现象，计算和试验结果的对比域略有出入，但计算结果准确捕捉到了反射激波位置及压力变化的细微结构，压力分布的波峰波谷也吻合较好。整体来看，采用AHL3D和相应的计算网格策略，是可以可靠评估本文所关心的内外流耦合条件下的一体化前体进气道模型的通流压缩性能的。

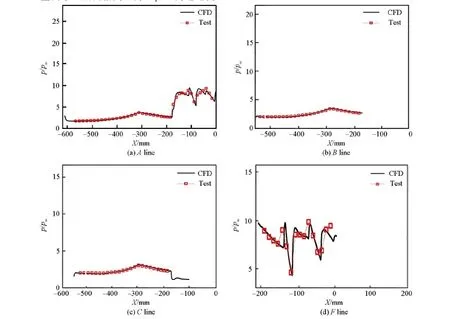
图7 来流马赫数为4.03，迎角为0°时，计算和试验静压分布对比Fig.7 Comparison of static pressure distributions of CFD and test simulation results at Ma∞=4.03, AoA=0°

3.2 实用化构型对性能影响分析

采用经过验证的数值软件和网格划分策略，分析了乘波前体及内收缩段前掠切除及黏性、钝度对图3(c)所示的原始理论构型性能的影响。计算条件同一体化CCWI的设计来流条件，即来流马赫数为5.5，迎角为0°。黏性计算时雷诺数同3.1节，即为3.09×107/m。

首先分析了乘波前体及内收缩段前掠切除对前体进气道基本压缩性能的影响。图8为切除构型在设计状态下的无黏流场马赫数三维结构及表面压力分布。在未做修型的完全乘波区域，激波紧贴前体侧缘，高压区被完全封闭在压缩面内。

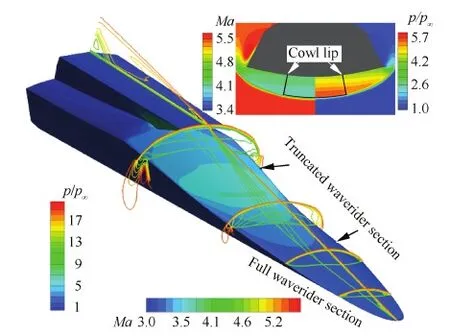
图8 几何切除一体化前体进气道的三维流场结构 Fig.8 Three dimensional flow field structure of geometrical truncated CCWI

在前体侧缘切除区域，靠近侧壁的激波有部分泄漏，但在流道捕获区域的激波结构未受任何影响，从唇口截面上的云图看，前体激波仍和唇口形状完全贴合，三维激波封口设计预期完全满足。表2 为原始构型和切除构型的内通道出口流动参数的无黏仿真结果的比较，质量加权马赫数、总压恢复、压升比及流量系数的差别甚微。以上结果说明，目前的侧向切除对一体化前体进气道设计状态下的流动压缩特性无影响。

表2理论、切除及钝度和黏性效应下CCWI的性能对比

Table2Performancescomparisonofprototype,truncatedandbluntnessviscousCCWI

ItemMamwptp/p∞ϕPrototype3．3980．75210．310．999Truncation3．4400．75010．340．994Bluntnessandviscosity2．780．5315．640．95

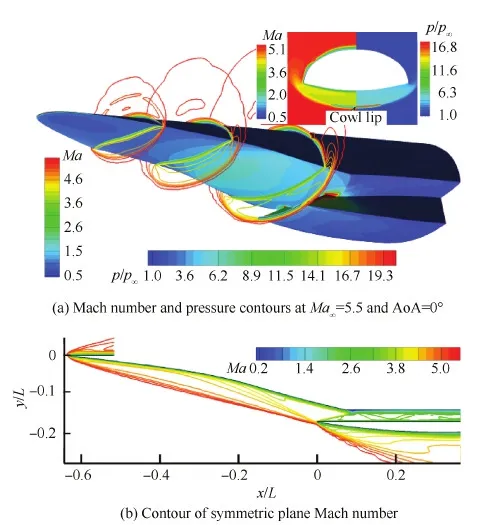
图9 设计状态CCWI三维流场结构及对称面马赫数和压力分布Fig.9 Three dimensional flow field structure and symmetric plane Mach number and pressure distribution of CCWI at design condition

在切除构型的基础上，进行了前缘钝度及隔离段整形处理。对其在设计点的性能进行了黏性湍流评估，以考核实用化修型及黏性效应对原始理论构型性能的影响，为将来该类构型的设计提供定量参考。图9(a)为实用化构型在来流马赫数为5.5，迎角为0° 时的空间马赫数等值线及机体表面压力云图。图9(b)为对称面的马赫数等值线图。由于钝度和黏性的影响，前体激波已经略微外溢，包裹住了进气道唇口；唇口的反射激波在机体侧出现了较弱的反射，且在唇口激波和机体侧边界层干扰区域存在较小的低速鼓包区，但未出现明显流动分离；完全乘波区域的激波略微溢出前体侧缘，但乘波特性依然明显。

图10为矩形隔离段出口流场的马赫数和压力云图。马赫数在核心区域的分布是比较均匀的，其质量加权数值为2.78。静压比在出口截面分布在14.0和16.5之间，质量加权数值为15.64，分布也是较为均匀的。质量加权的总压恢复系数为0.53；流量系数为0.95。表2最后一行列出了黏性、钝度及隔离段形变效应下的一体化CCWI构型的基本压缩性能。对比表2中的理论构型结果，在考虑黏性及实用化修型后，流量系数约有5%的降低；出口马赫数降低了0.6，约为来流马赫数的一半，符合超燃冲压发动机对流动压缩的需求；出口总压恢复减小0.2，压升增大了5倍的来流压力。前体进气道性能的损失主要是由钝度和黏性效应引起的。钝度和黏性效应，产生附着在壁面的低能边界层流动区域，边界层在进入进气道内通道后，连续反射的内通道斜激波串，作用到边界层上，强的逆压梯度进一步阻滞了边界层内的低速流动，使边界层增厚，造成了流动性能的损失。黏性效应无可避免，但可以考虑变前缘钝度设计，减小钝度对理论构型性能的影响，进一步考虑钝度和黏性条件下的边界层修正设计来减弱钝度和黏性效应对性能的负面影响。

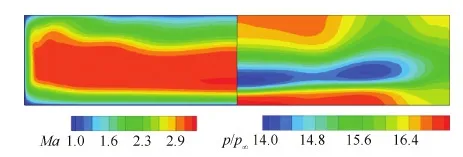
图10 设计状态CCWI隔离段出口马赫数和压力分布云图Fig.10 Mach number and pressure contours in isolator exit of CCWI at design condition

3.3 宽来流参数范围的一体化构型性能分析

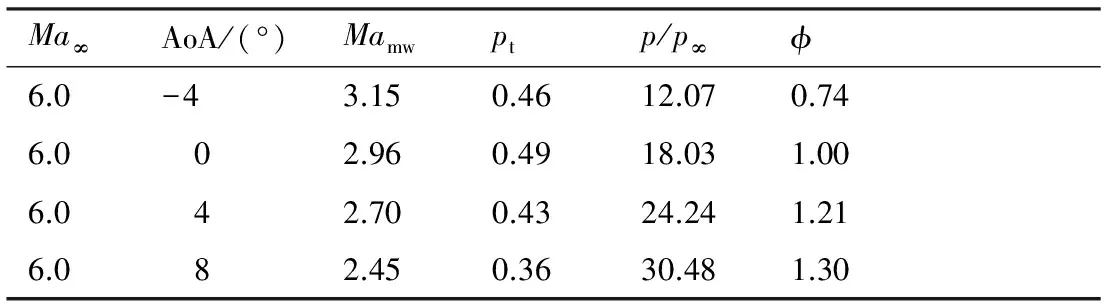
图11(a)为来流马赫数为6.0，迎角为0° 时，马赫数空间等值线及机体表面压力云图。由于来流马赫数大于设计马赫数5.5，若在无黏状态，前体激波应已进入唇罩内侧。但由于黏性和钝度的作用，来流马赫数为6.0，迎角为0° 时，前体激波正好交汇于唇口处，此时的流量系数恰好为1.0。前体全乘波区域的乘波特性依然明显。

图11(b)为来流马赫数为6.0，迎角在-4°～8° 时的对称面的马赫数等值线图。在迎角为0°时，前体激波和等熵压缩波正好相交于唇口；在迎角为 -4°、4° 和8° 时，前体激波都包裹住了唇口前缘。迎角为-4° 时，等熵压缩波基本相交于唇口前缘处，但前体激波距离唇口较远；而迎角为4° 和8° 时，等熵压缩波在唇口前已和前体激波相交，形成的交汇激波距离唇口前缘很近，预示在该迎角状态下的流量捕获性能较好。在所有迎角下，唇罩反射激波在内通道的反射并不强烈，但唇罩激波和机体边界层干扰区域已经出现了略微的流动分离区域，且随着迎角的增加而减小，原因是随着迎角的增大，前体对气流的压缩变强，此时的机体侧边界层变薄的缘故。

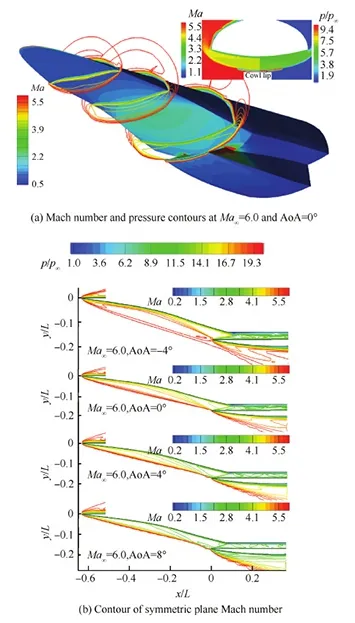
图11 来流马赫数为6.0时的流场结构和对称面马赫数等值线Fig.11 Flow field structures and symmetric plane Mach number at Ma∞=6.0

图12为马赫数为6.0，迎角为0°，隔离段出口截面马赫数和压力云图。从马赫数云图看，和图10比较，流动的核心区有所减小，此时的质量加权马赫数为2.96。压升散布的范围有所增大，说明不均匀度上升，其质量加权值为18.03。不均匀度增加的原因在于在内通道，相比较设计状态的情况，唇口的反射激波与机体侧物面相交于设计的消波点之后，激波反射在内通道增强了。表3给出了马赫数为6.0，不同迎角条件下的隔离段出口质量加权参数及流量系数。可以看出，流量系数较高，压升比和总压恢复系数较高，出口马赫数满足通常超燃冲压发动机入口需求(约为来流马赫数的一半)。本文及表2中的流量系数采用φ=m/ρ0v0s0计算，其中：m为进气道捕获流量；ρ0为来流密度；v0为来流速度;s0为迎角为0° 时的捕获面积。

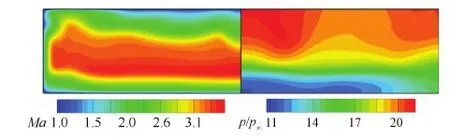
图12 来流马赫数为6.0，迎角为0° 时隔离段出口马赫数和压力云图Fig.12 Mach number and pressure contours in isolator exit at Ma∞=6.0 and AoA=0°

表3来流马赫数为6.0时的隔离段出口参数和流量比

Table3ParametersinisolatorexitandmassflowratiosatMa∞=6.0

Ma∞AoA/(°)Mamwptp/p∞ϕ6．0-43．150．4612．070．746．0 02．960．4918．031．006．0 42．700．4324．241．216．0 82．450．3630．481．30

图13(a)为来流马赫数为4.0，迎角为0° 时，空间马赫数等值线及机体表面压力云图。图13(b)为迎角在-4° ～8° 时的对称面的马赫数等值线图。在低马赫数端，前体激波已远离唇口前缘，但唇口截面捕获流管区域的马赫数分布仍然比较均匀；激波在前体侧缘有较明显的外溢现象，但高压区仍大部分封闭在前体压缩面内；等熵压缩面的压缩波和前体激波交汇于唇口外侧，且随着迎角的增加，交汇位置前移；各个迎角条件下，内通道的激波反射现象较弱，激波边界层作用区域未见明显的分离现象。

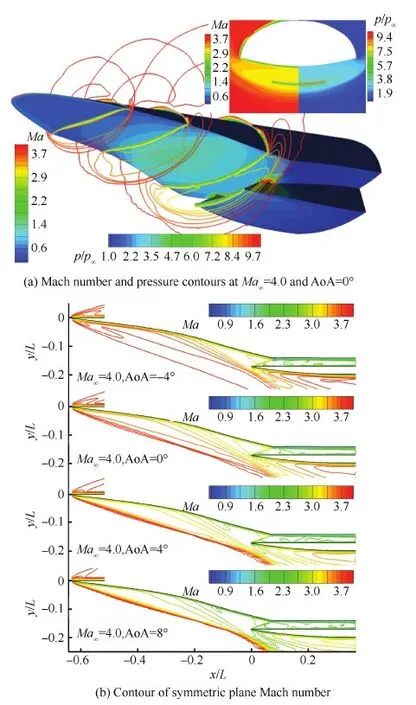
图13 来流马赫数为4.0时的流场结构和对称面马赫数等值线Fig.13 Flow field structures and symmetric plane Mach number at Ma∞=4.0

图14为来流马赫数为4.0，迎角为0° 时的隔离段出口马赫数和压力云图。从马赫数云图看，流动的核心区增大，且马赫数在核心区域分布均匀。压升分布也相对均匀，其数值在7.7～8.6。该状态下，质量加权马赫数为2.24，总压恢复系数为0.7，压升比为8.33，流量系数可达0.67。表4给出了迎角在-4°～8° 之间，隔离段出口质量加权参数及流量系数。总压恢复系数较高，0° 迎角时为0.7，且在0°～4° 迎角范围内还略有增加，这对小迎角飞行是有利的。流量系数较高，0° 迎角时为0.7左右。

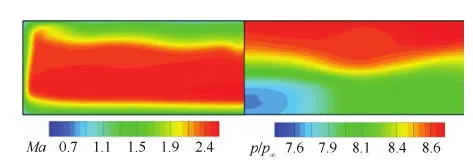
图14 来流马赫数为4.0，迎角为0° 时隔离段出口马赫数和压力云图Fig.14 Mach number and pressure contours in isolator exit at Ma∞=4.0 and AoA=0°

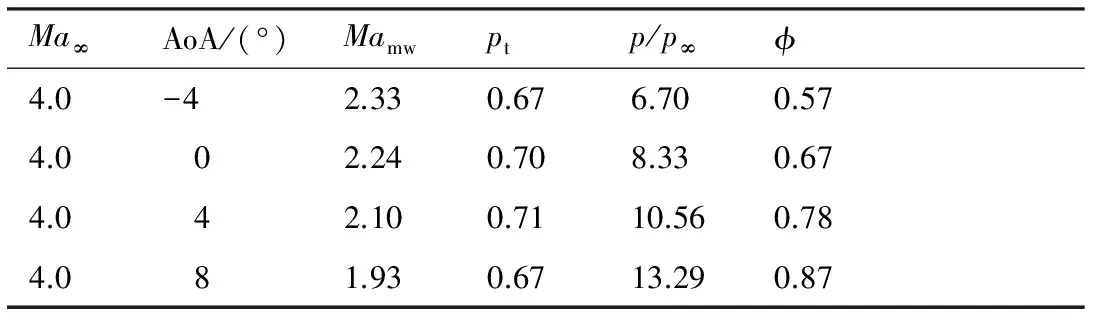
表4 来流马赫数4.0时的隔离段出口参数Table 4 Parameters in isolator exit at Ma∞=4.0

通过以上的分析表明，该实用化乘波前体进气道，具备较好的流动压缩能力。有关一体化构型的升阻特性，由于各种定义体系的差别，及考虑到需要站在飞行器的角度分析，这里不单独列出，但从前体的乘波特性上可以判断，该构型的升阻比，是好于同等条件下的升力体构型的。

3.4 与曲内锥乘波前体进气道的对比

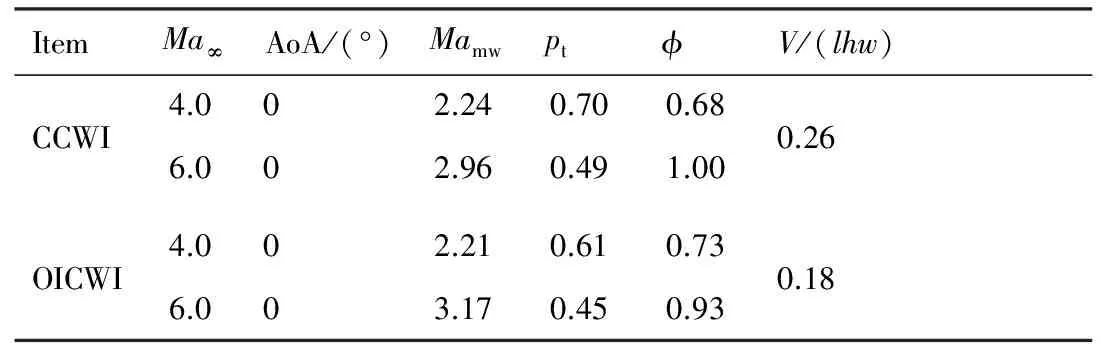
表5将CCWI的压缩性能及容积特性，同文献[16,18]的OICWI的对应特性进行了对比。同为考虑钝度、几何约束及黏性效应后的试验或数值仿真数据，在来流马赫数为4.0和6.0，迎角为0° 时，曲外锥和曲内锥乘波前体进气道的流动压缩能力类似，但总压恢复系数略高于后者。流量捕获系数在低马赫数段，OICWI的φ(0.73)略高于CCWI的(0.68)；而在高马赫数段正好相反。OICWI在经过侧缘切除及钝度修型后，对设计状态的流量捕获性能影响较大。容积性能，是采用2款构型至喉道处的体积V，除以各自到喉道处的长度l，最大宽度w和前体对称面前缘至喉道外罩下型面的高度h。外锥CCWI构型的容积率(0.26)明显优于内锥OICWI构型(0.18)，其外凸的前体压缩面，外形饱满，结构容积特性好，将为飞行器的装载性能的提升提供良好的构型保障，而较好的装载特性是实用化飞行器的基本要求。需要指出的是，这是两款基础型的乘波前体进气道的流动压缩性能的对比，它们的性能还可以通过对各自的基准流场的设计优化而进一步提升。

表5曲外锥和曲内锥乘波前体进气道性能对比

Table5PerformancecomparisonbetweenCCWIandOICWI

ItemMa∞AoA/(°)MamwptϕV/(lhw)CCWI4．002．240．700．686．002．960．491．000．26OICWI4．002．210．610．736．003．170．450．930．18

4 结 论

1) 创新性地提出并采用内外流匹配的一体化流线追踪技术，实现了曲外锥乘波体和类二元进气道符合气动压缩规律的整体式一体化设计。

2) 在设计状态，乘波前体及内收缩段切除，对理论构型的基本压缩性能无影响；考虑前缘钝度、隔离段修型及黏性效应后，流量系数仍达到0.95，整体压缩性能满足发动机入口需求。

3) 宽来流状态下的数值仿真结果表明，曲外锥乘波前体进气道具有较高的流量捕获率和较好的总压恢复性能，宽范围的压缩性能满足发动机的入口需求。

4) 同内锥乘波前体进气道相比，曲外锥乘波前体进气道的容积特性好，实用化修型对设计性能的影响小。

通过本文的研究，为新型曲外锥乘波体进气道同燃烧室和飞行器的一体化研究奠定了基础。

[1] RICHARD M, SCOTT M. X-51 development: A chief engineer’s perspective view[C]//17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference. Reston: AIAA, 2011: 13-17.

[2] KUCHEMANN D. The aerodynamic design of aircraft[M]. Oxford: Pergamon Press, 1978: 448-510.

[3] HEISER W H, PRATT D T. Hypersonic airbreathing propulsion[M]. Reston: AIAA Inc. Press, 1994: 32-33.

[4] HANEY J W, BEAULIEU W D. Waverider inlet integration issues: AIAA-1994-0383[R]. Reston: AIAA, 1994.

[5] BERENS T M,BISSINGER N C. Forebody precompression effects and inlet entry conditions for hypersonic vehicles[J]. Journal of Spacecraft and Rockets, 1998, 35(1): 30-36.

[6] BILLIG F S, BAURLE R A, TAM C J. Design and analysis of streamline traced hypersonic inlets: AIAA-1999-4974[R]. Reston: AIAA,1999.

[7] SMART M K. Design of three-dimensional hypersonic inlets with rectangular to elliptical shape transition[J]. Journal of Propulsion and Power, 1999, 15(3): 408-416.

[8] VIJAY S, ANDREW G, MARK S. Automated design optimization for the P2 and P8 hypersonic inlets[J]. Journal of Aircraft, 1997, 34(2): 308-316.

[9] MARY K L O, MARK J L. Optimized scramjet integration on a waverider[J]. Journal of Aircraft, 1992, 29(6): 1114-1123.

[10] TAKASHIMA N, LEWIS M J. Engine-airframe integration on osculating cone waverider-based vehicle designs: AIAA-1996-2551[R]. Reston: AIAA, 1996.

[11] O’BRIEN T F, MARK J L. Rocket-based combined-cycle engine integration on an osculating cone waverider vehicle[J]. Journal of Aircraft, 2001, 38(6): 1117-1123.

[12] SOBIECZKY H, DOUGHERTY F C, JONES K D. Hypersonic waverider design from given shock waves[C]//Proceedings of the 1st International Hypersonic Waverider Symposium. Washington, D.C.: NASA, 1990.

[13] RYAN P S, MARK J L. Design of an engine airframe integrated hypersonic missile within fixed box constraints: AIAA-1999-0509[R]. Reston: AIAA, 1999.

[14] YOU Y C, ZHU C X, GUO J L. Dual waverider concept for the integration of hypersonic inward-turning inlet and airframe forebody: AIAA-2009-7421[R]. Reston: AIAA, 2009.

[15] LI Y Q, AN P, PAN C J, et al. Integration methodology for waverider-derived hypersonic inlet and vehicle forebody: AIAA-2014-3229[R]. Reston: AIAA, 2014.

[16] 贺旭照, 周正, 倪鸿礼. 密切内锥乘波前体进气道一体化设计和性能分析[J]. 推进技术, 2012, 33(4): 510-515.

HE X Z, ZHOU Z, NI H L. Integrated design methods and performance analyses of osculating inward turning cone waverider forebody inlet(OICWI)[J]. Journal of Propulsion Technology, 2012, 33(4): 510-515 (in Chinese).

[17] HE X Z,LE J L, ZHOU Z, et al. Osculating inward turning cone waverider/inlet (OICWI) design methods and experimental study: AIAA-2012-5810[R]. Reston: AIAA, 2012.

[18] 周正, 贺旭照, 卫锋, 等. 密切曲内锥乘波前体进气道低马赫数性能试验研究[J]. 推进技术, 2016, 37(8)： 1455-1460.

ZHOU Z, HE X Z, WEI F, et al. The experimental studies of osculating inward turning cone waveriderforebody inlet (OICWI) at low Mach number conditions[J]. Journal of Propulsion Technology, 2016, 37(8): 1455-1460 (in Chinese).

[19] ZUCROW M J, HOFFMAN J D. Gas dynamics Vol.2: Multidimensional flow[M]. New York: John Wiley and Sons, Inc. Press, 1977: 112-266.

[20] BERNBARD H A. Design of supersonic inlets by a computer program incorporating the method of characteristics: NASA TN D-4960[R]. Washington, D.C.: NASA, 1969.

[21] HE X Z, LE J L,WU Y C. Design of a curved cone derived waverider forebody: AIAA-2009-7423[R]. Reston: AIAA, 2009.

[22] TRENT T, DAVID V W. Performance analysis of hypersonic shape changing inlets derived from morphing streamline traced flowpaths: AIAA-2008-2635[R]. Reston: AIAA, 2008.

[23] HE X Z,ZHAO H Y,LE J L. Application of wall function boundary condition considering heat transfer and compressibility[J]. Acta Aerodynamic Sinica, 2006, 24(4): 1138-1144.

[24] 0.6米×0.6米跨声速风洞(FL-23)[EB/OL].[2016-08-22].http://www.cardc.cn/DevRead.Asp?Channelld=4&Classld=19&ld=7#.0.6m×0.6 m transonic wind tunnel (FL-23)[EB/OL]. [2016-08-22].http://www.cardc.cn/Dev Read.Asp?Channelld=4&Classld=19&ld=7# (in Chinese).

(责任编辑： 张晗)

Design and performance analysis of practical curved cone waverider inlet

HEXuzhao*,LEJialing

LaboratoryofScienceandTechnologyonHypervelocity/ScramjetAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

The integration design method for the novel curved cone waverider forebody inlet (CCWI) is introduced, and a prototype CCWI is designed. The practical CCWI with rectangle exit isolator and leading edge bluntness is obtained under geometrical constrains. The cutting off and bluntness effects are evaluated using the validated numerical simulation tools. Reynolds average Navier-Stokes simulations are conducted at free stream Mach numberMa∞=4.0, 6.0, angle of attack (AoA) from -4° to 8°. The results show that the practical CCWI has high mass flow capture ratios and total pressure recovery at the simulation conditions. Its basic compression characteristics can meet the needs of scramjet combustors. The present study provides the possibilities for the integration study of CCWI with hypersonic vehicles and scramjet combustors.

waverider; inlet; integration; practical design; test verification; numerical simulation

2016-08-22；Revised2016-09-26；Accepted2016-11-04；Publishedonline2016-12-211520

URL：www.cnki.net/kcms/detail/11.1929.V.20161221.1520.012.html

NationalNaturalScienceFoundationofChina(51376192)

2016-08-22；退修日期2016-09-26；录用日期2016-11-04； < class="emphasis_bold">网络出版时间

时间：2016-12-211520

www.cnki.net/kcms/detail/11.1929.V.20161221.1520.012.html

国家自然科学基金 (51376192)

*

.E-mailhexuzhao@sina.com

贺旭照， 乐嘉陵． 曲外锥乘波体进气道实用构型设计和性能分析J． 航空学报,2017,38(6):120690.HEXZ,LEJL.DesignandperformanceanalysisofpracticalcurvedconewaveriderinletJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):120690.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0289

V235.213

A

1000-6893(2017)06-120690-11

*Correspondingauthor.E-mailhexuzhao@sina.com