执行器故障卫星的自适应模糊滑模容错控制*

屠园园 王大轶 李文博

1. 北京控制工程研究所, 北京100190 2. 北京空间飞行器总体设计部, 北京100094

执行器故障卫星的自适应模糊滑模容错控制*

屠园园1王大轶2李文博1

1. 北京控制工程研究所, 北京100190 2. 北京空间飞行器总体设计部, 北京100094

针对卫星控制系统执行器故障，考虑干扰与不确定性影响，设计了一种自适应模糊滑模容错控制器(AFSMC)。首先，将执行器故障、干扰以及模型不确定性统一描述为系统的广义总干扰；然后，为使系统能够在有限时间内快速稳定且避免奇异，设计了非奇异快速终端滑模控制器(NFTSMC)；其次，针对滑模系统固有的抖振现象，设计了自适应算法对系统广义总干扰进行补偿，减小了切换增益，并以自适应模糊系统逼近切换函数，柔化了输入信号，从而有效削弱了系统抖振，大大提高了控制精度；最后，对所提方法进行了数值仿真验证。

姿态跟踪；滑模控制；干扰补偿；自适应模糊；Lyapunov稳定性

随着航天技术的发展，越来越多的卫星在执行相关任务时，需要在机动过程中保持高精度的姿态稳定能力。结合实际工作环境，考虑运行过程中存在的干扰、噪声等恶劣情况，卫星的控制分系统不可避免地会发生故障[1-4]，尤其是长期处于高速运转状态的执行机构，其故障会严重影响控制精度[5-6]。为保证系统能够高精度地顺利完成既定任务，需提高其对执行器故障的鲁棒能力。因此，本文重点研究卫星在姿态跟踪过程中的容错控制问题。

由于滑模变结构控制技术在处理故障时无需故障诊断单元，具有良好的自主容错性能,且能克服系统各种不确定性因素的影响，对干扰和未建模动态具有较强的鲁棒性，近年来被广泛应用于航天器控制理论研究[7-10]。

然而，对滑模变结构控制而言，当系统轨迹到达切换面时，惯性使得运动点穿越切换面，产生抖振现象，不仅影响控制精度、增加能量消耗，还易激发系统中的高频未建模动态，破坏系统性能，甚至导致系统振荡或失稳，损坏控制部件。 针对该问题，一些学者提出了模糊滑模控制器的概念[11-13]，利用模糊系统对切换函数进行“模糊化”，以柔化控制信号，有效减弱系统由于不连续而引起的抖振现象。然而，由于模糊系统精度不高，自适应能力有限，难以有效抑制系统的突发故障、干扰以及模型不确定性等复杂因素对姿态精度的影响，因此限制了控制精度的进一步提高。

1 卫星运动建模

基于单位四元数，给出卫星运动学方程为：

(1)

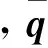
执行器故障的卫星动力学方程可以描述为：

(2)

其中，J∈3×3为卫星转动惯量，U∈3×m为执行器安装矩阵，Λ=diag{α1,α2,…,αm}为执行器失效因子矩阵，αi∈[0, 1],i=1,2,…,m；τ∈m为执行器输出列阵，f∈m，d∈3分别为执行器偏差故障和系统外部干扰。

qe=E(qd)q

(3)

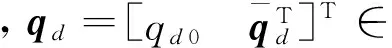
基于误差四元数，得到跟踪误差运动学方程：

(4)

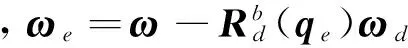
可推得航天器跟踪误差动力学方程：

(5)

考虑参数不确定性,假设实际的系统惯量矩阵为J=J0+ΔJ，其中，J0为已建模标称惯量矩阵，ΔJ为不确定部分，则式(5)可改写为：

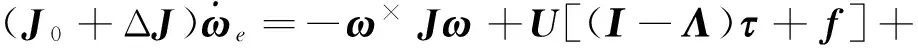
(6)

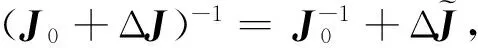
(7)

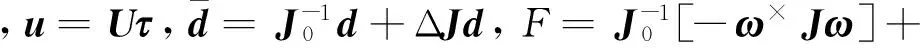
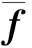
(8)

2 自适应模糊滑模控制器设计

为使卫星能够在有限时间内快速收敛，且有效避免奇异，本文选择非奇异快速终端滑模控制器为系统主控制器。相应滑模面表示如下：

(9)

其中，α,β>0, 1

p/q。

2.1 常规NFTSM控制器

常规的变结构控制器可以设计为：

u=ueq+uvss

(10)

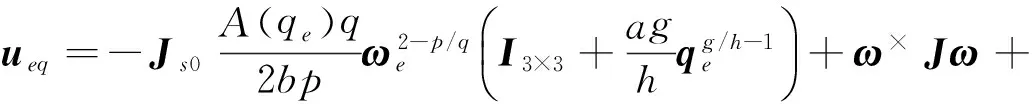
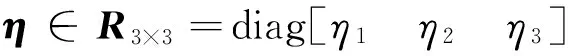
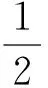
若存在：

(11)

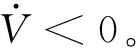
2.2 基于干扰补偿的NFTSM控制器

2.2.1 控制器设计

假设G∈3是系统的广义总干扰，包含执行器偏差故障、参数不确定性以及各种干扰力矩，满足若分别是G的估计值和理想观测值，则估计误差：

(12)

为使卫星能对期望姿态进行有效跟踪并加以保持，这里基于Lyapunov函数来设计控制器。选择Lyapunov函数如下：

(13)

其中，W-1∈3×3是正定对称矩阵。对上式求导：

(14)

结合式(9)和(14)可推得：

(15)

相应的控制器设计如下：

(16)

其中，φ是基于双曲正切的鲁棒控制项，

(17)

引入该项是为了补偿估计算法的近似误差。由双曲正切函数性质可知φ满足：STφ>0。

2.2.2 稳定性证明

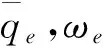
证明：选取Lyapunov函数如下：

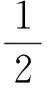
对时间t求导，并带入控制律式(16)得：

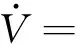
(18)

对比式(11)，可知引入干扰补偿后切换增益项η大大降低，有效削弱了系统的振颤。

当系统状态在滑模面上时，S=0，由滑模面定义式(9)得：

(19)

2.3 自适应模糊滑模控制器

控制律式(16)中的符号函数sign(S)是导致系统抖振的直接原因，非常不利于实际执行。为了能够既削弱系统抖振，又保持滑模变结构控制对执行器故障、模型不确定性以及干扰等实际因素的鲁棒性，本小节采用自适应模糊系统对符号函数进行逼近，该系统的输入为滑模面S，输出为符号函数的估计值。

设ufz=ηsign(S)，其各分量估计值为：

(20)

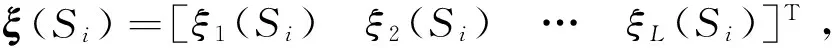
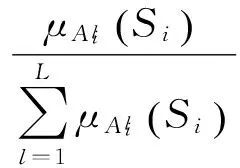
(21)

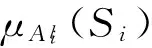
假设理想的调整参数向量为θ*，则实际调整参数的误差向量可以定义为：

(22)

基于Lyapunov函数可以推导参数θ的自适应律，建立如下Lyapunov函数：

(23)

对上式求导得：

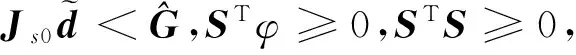
(24)

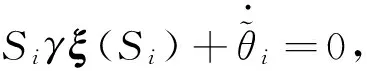
(25)

(26)

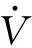
由式(22)可得调整参数的自适应变化律为：

(27)

对上述自适应模糊系统，定义模糊集：NB=负大，NM=负中，NS=负小，ZE=零，PS=正小，PM=正中，PB=正大。

隶属度响应函数为：

μNB=1/{1+exp(10(x+5π/6))}，
μNM=exp(-2(x+2π/3)2)，
μNS=exp(-2(x+π/3)2)，
μZE=exp(-2x2)，
μPS=exp(-2(x-π/3)2)，
μPM=exp(-2(x-2π/3)2)，
μPB=1/{1+exp(10(x-5π/6))}。

3 数值仿真

下面对本文提出的自适应模糊滑模容错控制器(AFSMC)的有效性进行数值仿真验证，并与常规NFTSMC、含干扰补偿的NFTSMC进行对比分析。期望运动模型参考文献[14]，卫星及控制器参数分别由表1～2给出，仿真结果如图1～4所示。

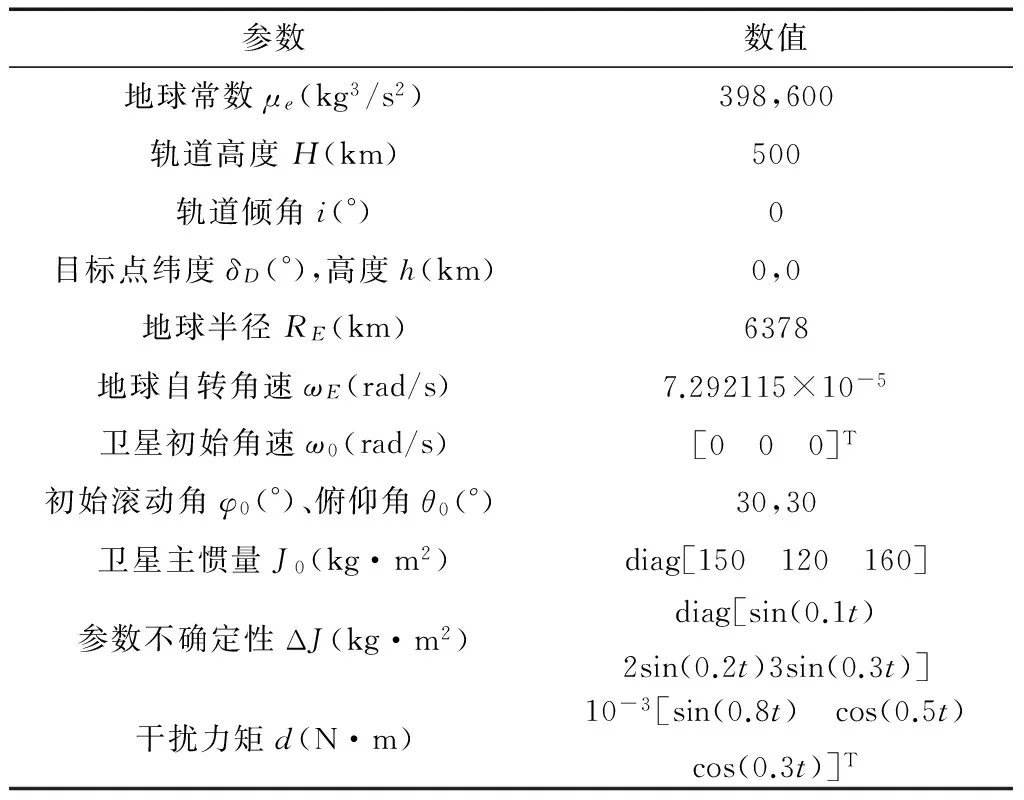
表1 卫星参数

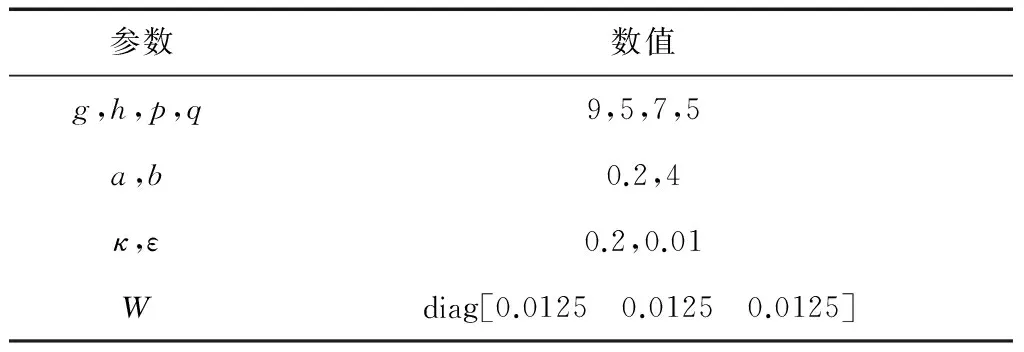
表2 控制器参数

观察图1～3可知，未发生故障时，在3种控制器作用下，系统均可于13s内稳定。采用常规NFTSMC的系统，受符号函数影响，存在明显抖振现象，稳定后控制力矩在0.0015N·m内振荡，误差角速度精度为0.003(°)/s，滚动轴与俯仰轴存在1°左右的偏差。引入干扰补偿以后，系统振颤现象明显减弱，控制力矩减小到0.001N·m，而控制精度并未显著提高。采用AFSMC的卫星，相比前2种情况，抖振现象明显削弱，误差角速度和姿态偏差角精度分别达0.0008(°)/s和 0.001°。

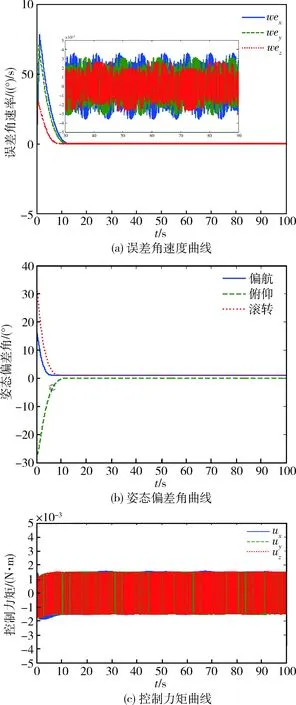
图1 常规NFTSMC仿真曲线

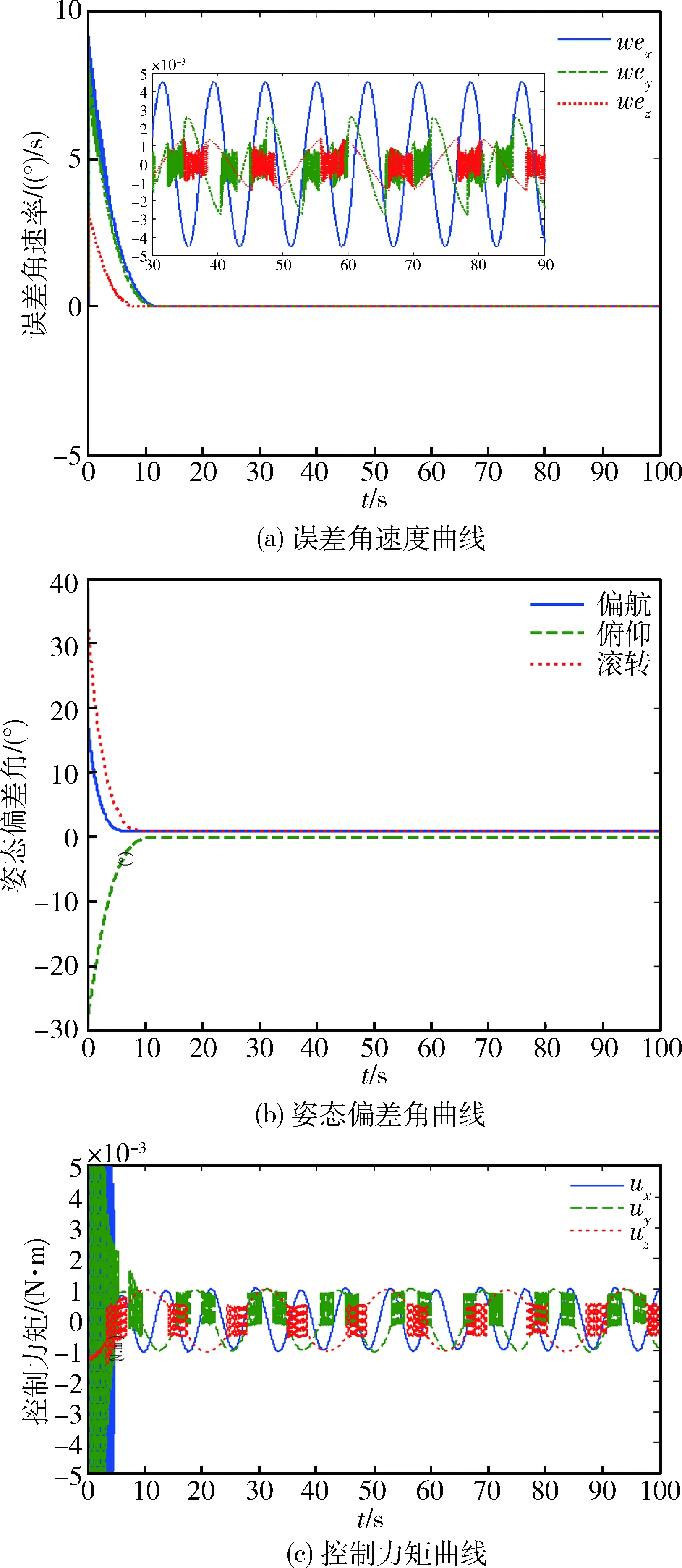
图2 加干扰补偿的NFTSMC仿真曲线

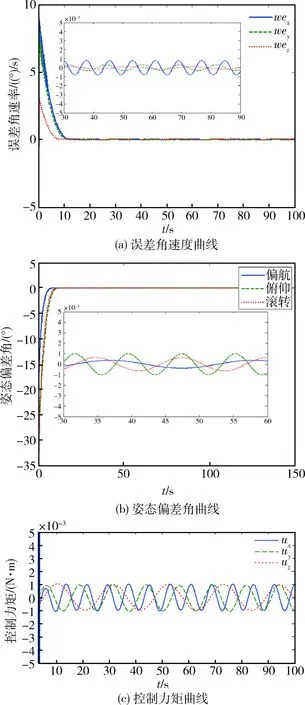
图3 AFNFTSMC仿真曲线

因此，可以得出结论：常规NFTSMC方法能够较好、较快地进行姿态跟踪，但变结构控制固有的抖振现象影响了系统实际性能、限制了姿态跟踪精度。在此基础之上，引入自适应干扰补偿器，可以减小切换增益，从而有效削弱系统振颤，但控制精度仍然没有显著提升。而本文所提AFSMC方法，进一步以自适应模糊模块逼近控制律中的切换项，不仅有效削弱了系统抖振，而且显著提高了控制精度。

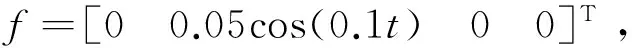
图4 AFNFTSMC容错曲线

4 结论

针对卫星姿态跟踪控制过程中可能发生的执行器故障，考虑干扰和模型不确定性等影响，设计了具有容错功能的自适应模糊滑模控制器。结合数值仿真，得到以下结论：该方法通过对系统广义干扰(执行器故障、干扰以及模型不确定性)进行实时补偿，减小了切换增益，并以自适应模糊系统来逼近切换函数，柔化了输入信号，有效削弱了滑模系统的固有抖振现象，大大提高了控制精度，无论是对于执行器失效故障还是偏差故障，均具有较高鲁棒性，能够使系统在故障以后，仍然能够维持在理想的精度范围内，具有一定的工程实际意义。

[1] Gao Z, Ding S X, Cecati C. Real-time Fault Diagnosis and Fault-tolerant Control [J]. IEEE Transactions on Industrial Electronics, 2015, 62(6):3752-3756.

[2] 李文博，王大轶，刘成瑞. 动态系统实际故障可诊断性的量化评价研究[J]. 自动化学报, 2014, 41(3):497-507.(Li Wenbo, Wang Dayi, Liu Chengrui. Quantitative Evaluation of Actual Fault Diagnosability for Dynamic Systems [J]. Acta Automatica Sinica, 2014, 41(3):497-507.)

[3] 段文杰，王大轶，刘成瑞．卫星控制系统离散积分滑模容错控制[J]．控制理论与应用，2015，32(2)：133-141. (Duan Wenjie, Wang Dayi, Liu Chengrui. Discrete-Time Integral Sliding-Mode Fault-Tolerant Controller for Satellite Control System [J]. Control Theory and Applications, 2015, 32(2): 133-141.)

[4] 项昌毅,杨浩,程月华,姜斌,刘成瑞. 卫星姿态控制系统的可重构性指标分配[J]. 航天控制, 2014,32(2):46-52. (Xiang Changyi, Yang Hao, Cheng Yuehua,et al. Reconfigurable Allocation of Satellite Attitude Control System[J]. Aerospace Control, 2014, 32(2):46-52.)

[5] 王世新, 邢琰, 王大轶. 基于能耗最优的卫星姿控系统推力器可重构性设计[J]. 航天控制, 2015, 33(5):46-53. (Wang Shixin, Xing Yan, Wang Dayi, et al. Reconfigurability Design for Thrusters of Satellite Attitude Control System Based on Optimal Energy Consumption[J]. Aerospace Control, 2015, 33(5):46-53.)

[6] 徐赫屿, 王大轶, 李文博. 卫星姿态控制系统的可重构性量化评价方法研究[J]. 航天控制, 2016, 34(4):29-35. (Xu Heyu, Wang Dayi, Li Wenbo. A Reconfigurability Evaluation Method for Satellite Control System Based on Gramian Matrix [J]. Aerospace Control, 2016, 34(4):29-35.)

[7] Vadali S R. Variable-structure Control of Spacecraft Large-Angle Maneuvers [J]. Journal of Guidance, Control and Dynamics, 1986, 9(2): 235-239.

[8] Wang B Q, Gong K, Yang D, Li J F. Fine Attitude Control by Reaction Wheels using Variable-Structure Controller [J]. Acta Astronautica, 2003, 52: 613-618.

[9] Ding S H, Li S H. Sliding Mode Control of Spacecraft Attitude with Finite-Time Convergence [C]. Proceedings of the 6th World Congress on Intelligent Control and Automation, Dalian, China. 2006: 830-834.

[10] 管萍，陈家斌．挠性卫星的自适应模糊滑模控制[J]. 航天控制, 2004, 22(4) :62-67.( Guan Ping, Chen Jiabin. The Adaptive Fuzzy Sliding Mode Control for Flexible Satellite [J]. Aerospace Control, 2004, 22(4) : 62-67).

[11] Chenga C H, Shua S L, Chengb P J. Attitude Control of a Satellite Using Fuzzy Controllers [J]. Expert Systems with Applications, 2009, 36: 6613-6620.

[12] 王蜀泉，尹逊和，赵光恒．用于卫星姿态机动控制的一种自适应模糊控制器 [J]．空间科学学报，2006，26(1):54-58．(Wang Shuquan, Yin Xunhe, Zhao Guanheng. An Adaptive Fuzzy Controller for Satellite Maneuver Control [J]. Chin. J. Space Sci., 2006, 26(1): 54-58.)

[13] Li J, Post M, Lee R．Real-Time Nonlinear Attitude Control System for Nanosatellite Applications [J]．Journal of Guidance Control，and Dynamics，2013，36(6):1661-1671.

[14] 叶东, 屠园园, 孙兆伟. 面向非沿轨迹成像的切比雪夫神经网络滑模姿态控制[J]. 航空学报, 2015, 36(9):3092-3104. (Ye Dong, Tu Yuanyuan, Sun Zhaowei. High-Precision Attitude Tracking Control System for Next-generation Smart Imaging Satellite Using Chebyshev Neural Network[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9):3092-3104.)

AFaultTolerantControlSystembyUsingAdaptiveFuzzySlidingModeforSatelliteswithActuatorFaults

Tu Yuanyuan1, Wang Dayi2, Li Wenbo1

1. Beijing Institute of Control Engineering, Beijing 100190, China 2. Beijing Institute of Spacecraft System Engineering, Beijing 100094, China

Anadaptivefuzzyslidingmodecontroller(AFSMC)isdesignedforthesatelliteregardingtheactuatorfaults,disturbanceandmodeluncertaintyduringtheattitudetrackingprocess.Firstly,thetrackingerrordynamicandkinematicmodelsarebuiltbasedonquaternionerror,wheretheactuatorfaults,disturbanceandmodeluncertaintyarecombinedwithageneralinterference.Then,anonsingularandfastterminalslidingmodecontroller(NFTSMC)isderivedasthemaincontrollertoguaranteethesystemstabilityinlimitedtimeforavoidingthesingularity.Byconsideringthechatteringinherentinslidingmodestructure,anadaptivelawisintroducedtocompensatethegeneralinterferencewhichefficientlyweakensthechatteringbyreducingtheswitchgain.Inordertofurtherimprovetheprecisionofthesystem,anadaptivefuzzysystemisusedtoapproximatethesymbolicfunctionintheslidingmodecontrol.Finally,numericalsimulationsontheattitudetrackingcontrolofspacecraftinthepresenceofenvironmentaldisturbanceandparametersuncertaintiesareperformed,whoseresultsshowthesystemusingAFSMCcanstabilizewithin13-and

*国家杰出青年科学基金(6152530);国家自然科学基金(61690215, 61640304, 61573060, 61203093)

theprecisionofattitudeangleandangularvelocitycanbe0.001°and0.0008(°)/s,respectively.Inaddition,thismethodcanmeettherequirementsoffault-tolerancewithfasterconvergencespeedandbetterrobustnessbycomparingwiththeconventionalNFTSMC.

Attitudetracking;Slidingmodecontrol;Interferencecompensation;Adaptivefuzzy; Lyapunovstability

V467

A

1006-3242(2017)05-0051-07

2017-04-27

屠园园(1992-)，女，江苏人，硕士研究生，主要研究方向为控制系统可重构性研究；王大轶(1973-)，男，黑龙江人，博士，研究员，主要研究方向为航天器制导、导航与控制，卫星可重构性及可诊断性评价与设计;李文博(1984-)，男，天津人，博士，高级工程师，主要研究方向为航天器可诊断、可重构性评价与设计。