基于Amorphous的无线传感器网络定位算法研究
北京信息科技大学自动化学院,北京 100101
一、引言
无线传感器网络(Wireless Sensor Networks)[1-3]作为一种全新的信息获取和处理技术,是当前在国际上备受关注的、涉及多学科高度交叉的前沿热点研究领域。
无线传感器网络的关键支撑技术之一是定位问题,定位问题也是无线传感器网络应用以及其他研究的基础,如地理环境监测、军事侦察、交通路况监测、抢险救灾、医疗卫生中对病人的跟踪等,所获取的监测数据需要有相应的位置信息,否则,这些数据就是不确切的,甚至会失去采集数据的意义。
全球定位系统(GPS)可以为地球表面绝大部分地区(98%)提供准确的定位。但是受到成本、功耗、体积等因素的限制,在大规模的无线传感器网络中,为每个传感器节点都安装GPS设备是不太实际的方法。所以现有的一些定位方法中只是让少数传感器节点配备有GPS设备,然后通过一些数学的方式来估算未知传感器节点的位置。
根据定位过程中是否测量实际节点间的距离,定位算法可分为:距离相关(Range-based)定位算法和距离无关(Range-free)定位算法。其距离相关的定位算法需要测量相邻节点间的绝对距离或方位,并利用节点间的实际距离来计算位置节点的位置,定位精度高,但对节点本身硬件要求较高。距离无关的定位算法是根据网络连通性等信息,利用节点间的估计距离计算节点位置,成本低、功耗小、抗噪能力强且硬件设备简单。Amorphous定位算法就是一种距离无关的定位算法。
Amorphous定位算法是由麻省理工大学的Radhika Nagpal等人提出的[4]。此算法是通过计算未知节点与锚节点之间的跳数,估计平均每跳距离,用未知节点与锚节点之间的跳数乘以平均每跳距离来计算未知节点到锚节点的距离,再利用最小二乘法来计算位置节点的未知。Amorphous定位算法简单,无需测距,实现容易。
现阶段对Amorphous定位算法的改进方法主要有:跳数修正[5];将已定位的未知节点转化为锚节点来帮助其他节点进行定位[6];而对Amorphous定位算法本身的参数优化研究较少。
本文详细分析了Amorphous定位算法本身的参数,并通过仿真对参数进行优化。仿真结果表明,通过参数优化可以有效的提高Amorphous定位算法的定位精度。
二、Amorphous定位算法步骤
Amorphous[4-6]定位算法计算未知节点的位置的过程可以分为下面三个步骤:
1、计算未知节点到各个锚节点的跳数
网络中的锚节点周期性的向邻居节点发送携带位置信息的跳数数据包,并且在初始化时将跳数值设置为0,当锚节点的邻居节点首次收到此广播信息后,首先更新自身到锚节点的最小跳数和对应的锚节点的信息,然后再将更新后的信息转发给其邻居节点,直到检测区域内所有待定位的节点都得到其到各锚节点的最小跳数。然后利用下式计算未知节点到各锚节点的跳数:
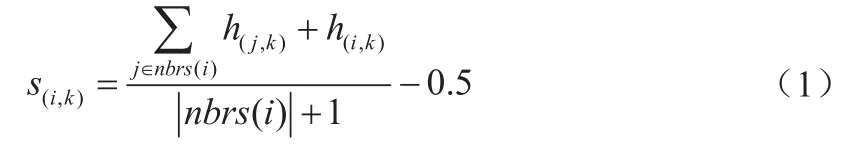
其中,s(i, k)—未知节点i到锚节点k的跳数;
h(j, k)—未知节点j到锚节点的k的最小跳数;
h(i, k)—未知节点i到锚节点k的最小跳数;
nbrs(i) —未知节点i的邻居节点的集合;
|nbrs( i)|—未知节点i的邻居节点的数目。
2、估算平均每跳距离
Amorphous算法是离线计算网络每跳距离的,它需要在网络部署之前就知道网络的平均连通度,下式可以离线计算网络平均连通度:

其中,nlocal—网络的平均连通度;
n—节点总数;
S—检测区域的面积;R—节点的通信半径。
然后,用下式计算平均每跳距离:
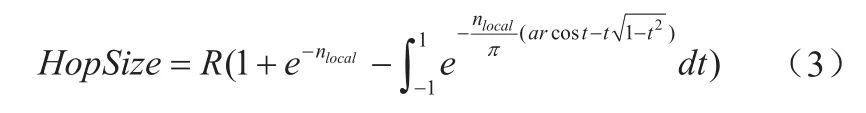
其中,HopSize—平均每跳距离;
nlocal—网络的平均连通度;
R—节点的通信半径。
Amorphous算法根据未知节点到各个锚节点的跳数和平均每跳距离来计算未知节点到各个锚节点的距离,计算公式如下:

其中,d(i,k)—未知节点i到锚节点k的距离;
HopSize—平均每跳距离;
s(i, k)—未知节点i到锚节点k的跳数;
3、计算未知节点的位置。
当未知节点获得到至少3个锚节点的距离时,可以通过最小二乘法来计算未知节点的坐标。未知节点X=(x,y)T的坐标可以通过下面的公式计算得到:

其中,(xn , yn) —表示第n个锚节点的坐标;
dn—表示未知节点到第n个锚节点的距离。
分别用公式(5)前(n-1)个方程减去最后一个方程,得:
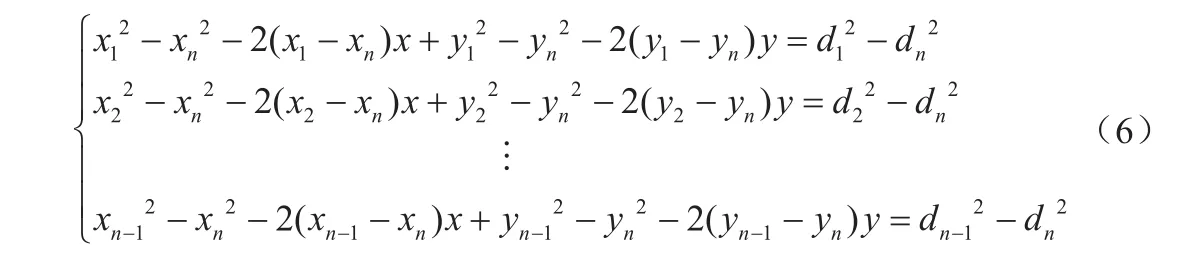
式(6)的线性方程可以表示成
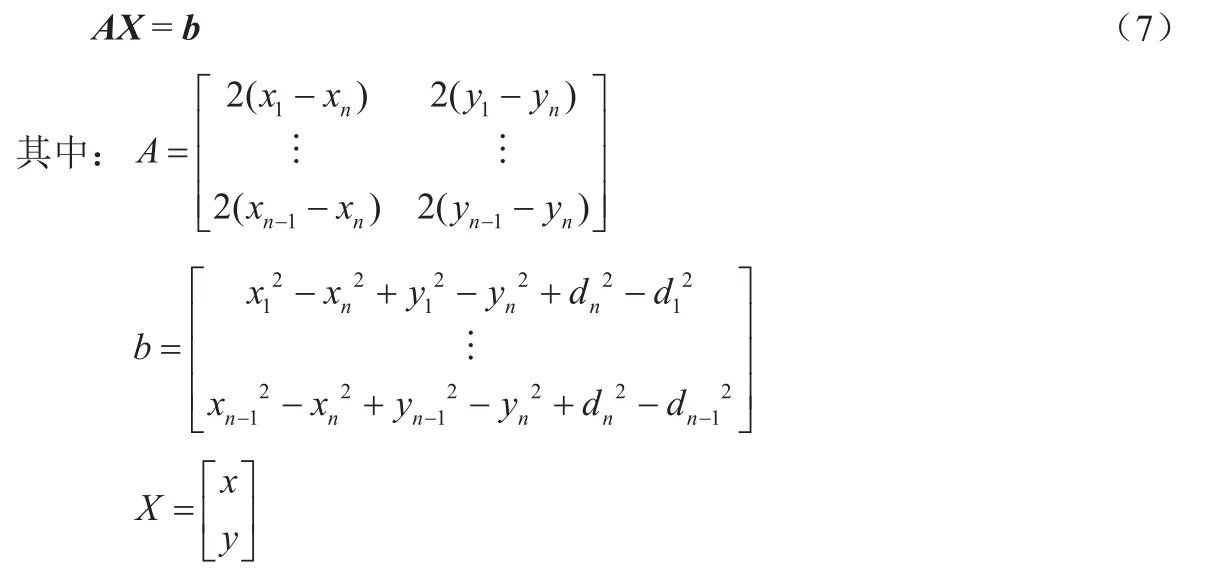
未知节点X 的坐标可以用标准的最小均方差估计方法得到,计算公式如下:

三、Amorphous算法的参数分析
1、锚节点的数目
Amorphous算法中,未知节点的位置是通过求解AX=b得到的。因为所有节点都是随机分布的,当有些锚节点的位置重叠或者距离很近,或者有些锚节点分布在一条直线上时,使得包含锚节点位置信息的矩阵A在求逆矩阵的时候出现奇异矩阵或者NAN等情况,进而影响未知节点的定位精度。
2、节点的通信半径
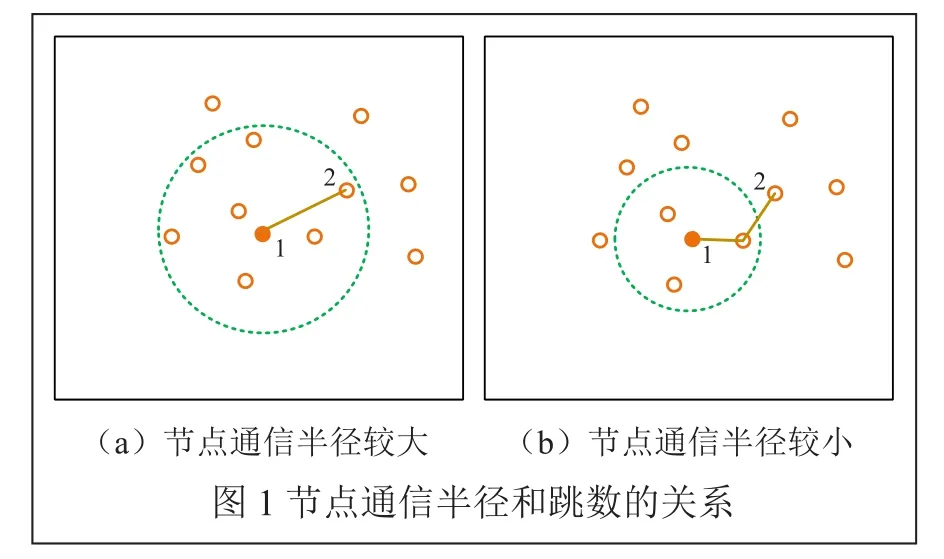
因为节点的跳数和节点的通信半径是有关系的,节点的通信半径发生变化时,节点之间的跳数也会发生变化。如图1所示,虚线圆表示1号节点的通信半径,图1(a)的节点通信半径大于图1(b)的节点通信半径,1号节点和2号节点的跳数在图1(a)中是1跳,在图1(b)中是两跳。而Amorphous算法正是利用未知节点与锚节点的跳数来计算未知节点的位置,所以节点的通信半径对定位精度有着很大的影响。
3、总节点的数目
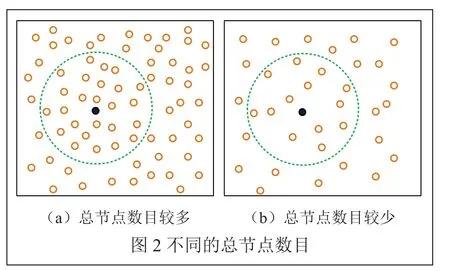
如图2所示,虚线圆表示黑色未知节点的通信半径,从图2中可以看出,当图2(a)和图2(b)的节点通信半径相同时,黑色未知节点的邻居节点数目不同,那么根据式(1)计算得出的黑色未知节点到锚节点k的跳数就会不同。进而最终得到的未知节点的定位精度就会不同。
四、仿真结果与分析
在100m×100m的无线传感器网络监测范围内,节点随机的分布,利用MATLAB 仿真工具,给出了当锚节点个数、节点通信半径和总节点数发生变化时,利用Amorphous算法得到的节点的定位误差的变化,仿真中给出的每一个数值都是50次仿真结果求得的平均值,并且给出了仿真结果分析。
当总节点个数为100,锚节点个数从3~30变化时,分别对节点通信半径R为20m、30m、40m时节点的定位误差进行了仿真。仿真结果如图3所示。
从图3中可以看出,节点通信半径不同时,当锚节点个数为10时,定位误差能达到较小值;当锚节点个数从3~8变化时,节点定位误差迅速减少;当锚节点个数继续增加时,定位误差趋于平缓。说明通信半径不同,当锚节点达到一定数量时,其对节点定位误差的影响将减小。

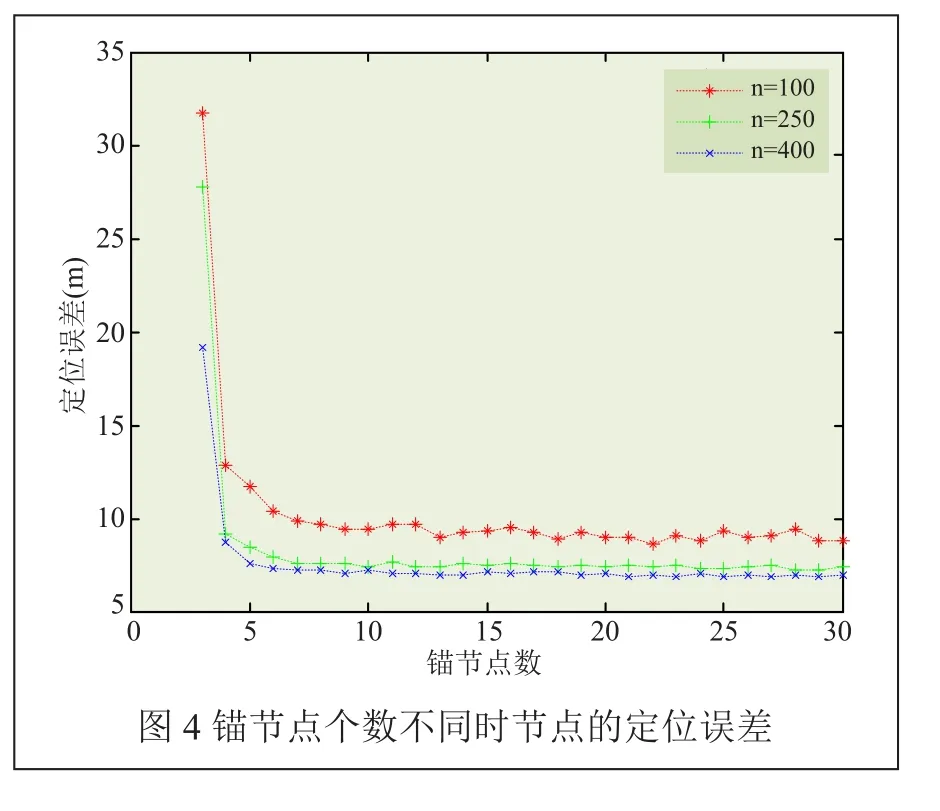
当节点通信半径为30m,锚节点个数从3~30变化时,分别对总节点数n为100、250、400时节点的定位误差进行了仿真。仿真结果如图4所示。
从图4中可以看出,总节点数目不同时,当锚节点个数为10时,定位误差能达到较小值;当锚节点个数从3~8变化时,节点定位误差迅速减少;当锚节点个数继续增加时,定位误差趋于平缓。说明总节点数目不同,当锚节点达到一定数量时,其对节点定位误差的影响将减小。
从图3和图4可以看出,当节点通信半径和总节点个数发生变化时,锚节点个数为10时,节点的定位误差能降到较小值。因为锚节点自身的成本比一般节点要高,所以在100m×100m的监测区域中,利用Amorphous算法进行定位时,取10个锚节点即可。
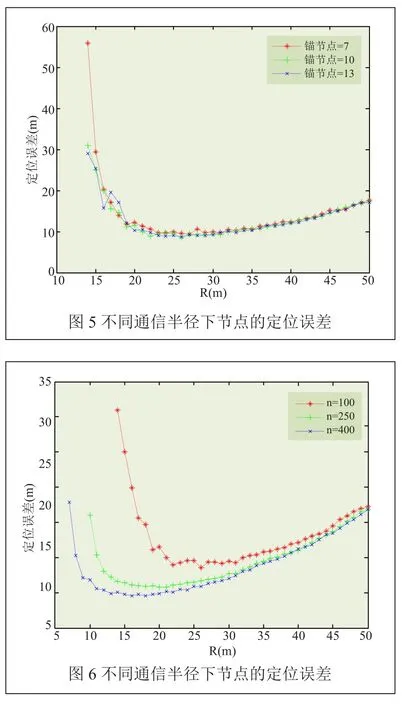
当总节点个数为100,通信半径从14~50变化时,分别对锚节点个数为7、10、13时节点的定位误差进行了仿真。仿真结果如图5所示。
从图5中可以看出,当通信半径从14~20m变化时,节点定位误差迅速减小,并且在通信半径为23m时定位误差达到了最小值,当通信半径继续增加时,节点的定位误差呈上升的趋势。说明在总节点个数为100,锚节点个数不同时,存在最优的通信半径。
由图3、4和5可以得出,在100m×100m的监测区域中,总节点个数为100时,随机分布10个锚节点,节点通信半径为23m时,定位误差可以达到较小值。
当锚节点个数为10且通信半径发生变化的情况下,对总节点个数为100、250、400时节点的定位误差进行了仿真。仿真结果如图6所示。
从图6中可以看出,总节点个数不同时,节点的最优通信半径也不同。当总节点个数为100时,在通信半径为23m时,节点定位误差可以达到较小值。当总节点个数为250时,在通信半径为16m时,节点定位误差可以达到较小值。当总节点个数为400时,在通信半径为13m时,节点定位误差可以达到较小值。
五、结论
本文对基于Amorphous的无线传感器网络定位算法进行了研究。 仿真结果表明,在100m×100m的无线传感器网络监测区域内,当锚节点个数连续变化时,在不同的总节点数目和通信半径下,锚节点数目达到一定数量时,其对节点定位误差的影响将减小;当通信半径连续变化时,总节点数目为100时,在不同的锚节点个数下,存在最优通信半径使定位误差达到最小值;当通信半径连续变化时,锚节点个数为10时,在不同的总节点个数下,存在不同的最优节点通信半径使定位误差达到最小值。所以利用最优节点通信半径使定位误差达到最小值。所以利用Amorphous算法进行定位时,由于传感器节点本身能量的限制和锚节点成本较高的原因,可以选择较优的参数来降低节点的定位误差。

