三维有偏权值张量分解在授课推荐上的应用研究

姚敦红，李石君，胡亚慧,3



三维有偏权值张量分解在授课推荐上的应用研究

姚敦红1,2，李石君2，胡亚慧2,3

(1. 怀化学院计算机科学与工程学院 湖南怀化 418000；2. 武汉大学计算机学院 武汉 430072; 3.空军预警学院四系 武汉 430010)

为解决现今学校授课安排无推荐依据这一实际问题，首先给出了一系列形式化方法用于规约教师的专业基础、课程难度及教学评价；定义了一种加权函数计算出每组专业基础、课程难度和教学评价的综合有偏权值；构建了一种基于“教师-课程-评价-权值”四元关系的三维有偏权值张量模型，张量元素使用综合有偏权值。在此基础上，设计了一种基于Tucker分解的算法，对张量进行高阶奇异值分解(HOSVD)得到降维后的近似张量，按课程分类实现了Top_授课推荐。实验结果表明，当迭代阈值达到一个合理值时，该方法能实现精准授课推荐，可作为一种新的智能化授课推荐方法应用于各类学校。

数据规约; 授课推荐; 张量分解; 三维有偏权值张量

推荐系统是对用户历史行为数据进行分析、预测并主动为用户给出相关推荐的系统。自文献[1]推出第一个推荐系统以来，涌现出了大量的推荐系统，特别是在电子商务、社交网络、搜索引擎等方面，如亚马逊基于兴趣的广告推荐、NEC研究院的CiteSeer搜索引擎、IBM的Websphere电商平台、阿里云推荐、京东推广、百度推广、博客挖掘、社交推荐等。这些推荐应用的实现一般是根据用户行为数据建立起的“用户-项目”二元关系挖掘分析而得。随着社会化标签的出现，又出现了“用户-产品-标签”的三元关系，使个性化推荐更趋向精准。

目前，推荐系统常用的技术有基于欧氏距离、Pearson相关系数、余弦相似性和Tanomi等最近邻启发式协同过滤推荐算法[2]；有基于上下文感知模型、潜在因子模型、贝叶斯模型、信任感知模型、聚类模型、最大熵模型[3]等协同过滤推荐算法；有以决策树、神经网络、向量、TF-IDF、自适应过滤、阈值设定等基于内容的推荐算法；还有其他如关联规则推荐、效用推荐、知识推理等算法，以及使用标签的图、标签的FolkRank、层叠、加权、变换、标签层次聚类[4]和张量分解的组合推荐算法等。

应用张量分解算法进行个性化推荐，在近年来也有了一些研究，文献[5-7]采用了融合某种关系或附加某种标签信息的张量分解推荐算法。文献[8-10]也有采用加权张量模型，即通过提取标注关键特征，再得出一个权值作为张量元素。

在现有研究中，还未曾涉及学校授课推荐。一直以来，学校授课安排没有一种好的推荐依据，很多是随教师意愿而为，或是强加给教师，这些方式未能使教学达到最优效果，难以提高教学质量。所以，在学校多年大量的教学数据中进行分析挖掘，找到一种实现精准授课推荐的方法，具有一定的现实意义和实用价值。

本文借鉴文献[11]的四元元组张量分解算法，优化文献[12]中提出的张量稀疏问题，设计一种基于Tucker张量分解的算法。并利用历史教学数据集进行授课推荐实验，验证该方法在授课推荐上的准确性。

1 基本概念

张量是高维数组的总称[14]，一维张量是向量，二维张量是矩阵，三维或以上的张量为高阶张量[6]。张量分解即HOSVD，是对高维数据进行特征提取，或是一种低秩逼近。常见的张量分解模型有：CP模型、Tucker模型[15]。Tucker模型将维张量分解成个维度上的低秩特征矩阵与一个核心张量的乘积，其本质是一种高阶主成分分析。如三维张量的Tucker分解为：

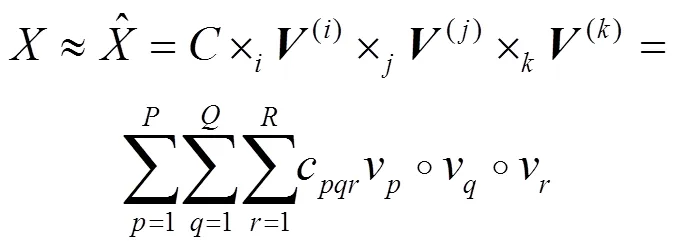
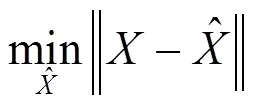
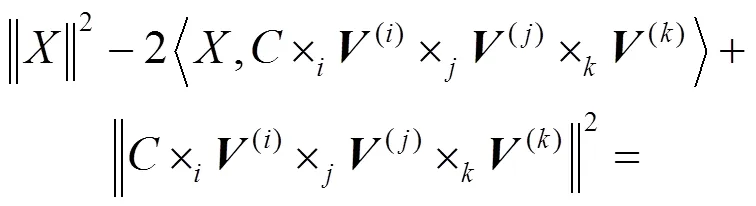
2 数据预处理

为构建用于授课推荐的有偏权值张量模型，和适应使用基于Tucker张量分解算法的要求，需对采集得到的相关教学数据进行预处理。首先从教师信息表、课程信息表及学生评教表等多个数据库表中，采用ETL方式构建一个事实星座模式的教学信息数据仓库，其结构如图1所示。图中，Course ID表示课程编号，Eva表示综合评价值，Sf(1)表示第1毕业学校因子，Sf(2)表示最后毕业学校因子，Pdb表示专业基础度。

然后采用下述定义对数据仓库中的相关属性进行规约处理：

定义1 毕业学校因子(school factor,Sf)：用来规约教师的毕业学校，按下列规则赋值，毕业于“985工程”与“211工程”高校Sf=0.4，毕业于“211工程”高校Sf=0.3，毕业于其他一本院校Sf=0.2，毕业于二本及以下院校Sf=0.1。

定义2 学位系数(degree coefficient,Dc)：用于规约教师取得的学位，本文约定博士、硕士、学士和无学位的Dc分别取0.4、0.3、0.2和0.1。

图1 事实星座模式结构图

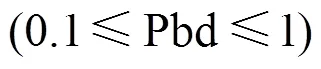
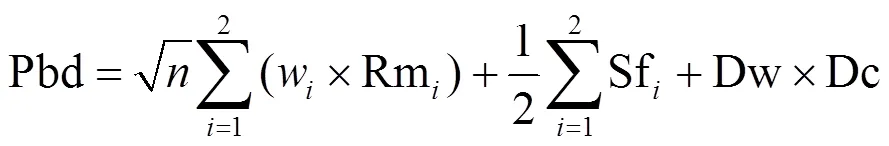
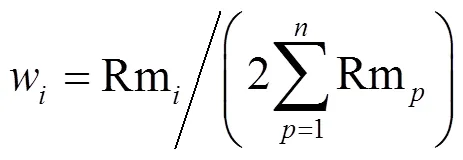
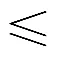
定义4 课程难度系数(curriculum difficulty coefficient, Cdc)(0.1≤Cdc≤1)：用于规范课程难度的指标，值越大表示课程难度越大。为使课程难度系数的评定趋于公认值，邀请校内外该专业优秀毕业生及专家教师在课程难度系数网上问卷调查，问卷调查中为每一专业的每门课程给出1～10个选项，每个专业总问卷份数不少于指定的阈值(如200)。然后将每门课程的难度系数规范化至区间[min，max] (本文中设min为0.1，max为1.0)上的一个难度系数，表示为：

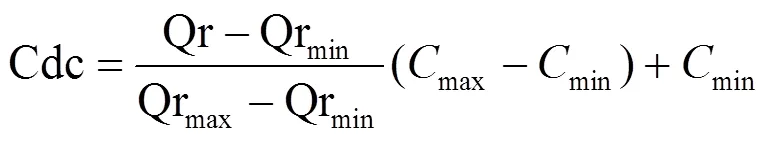
式中，Qr表示某门课程按专家教师问卷调查所占权重(0<<1)得到的难度值：

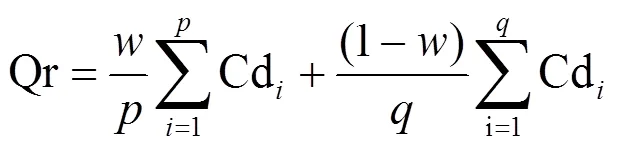
式中，为某专业回收的教师专家问卷份数；为回收的学生问卷份数；Cd为第门课程在问卷中所给出的难度系数值。

定义5 教师授课综合评价值(evaluation, Eva) (0.1≤Eva≤1)：表示教师所授的某一门课程总的综合评价分，分值越高表示越受欢迎。可采用最小-最大规范化方法将Eva规范化至区间[min，max](本文设min为0.1，max为1.0)上的一个综合评价值，表示为：

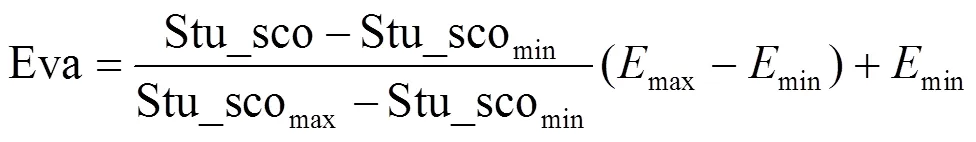
式中，Stu_scomin为某专业内所有课程中评价最低分值；Stu_scomax为评价最高分值；Stu_sco表示某教师所授同一课程，在个学期上学生评价分的总平均值：

3 模型及算法设计

3.1 三维有偏仅值张量模型

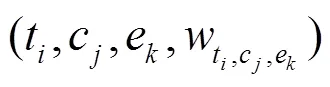
在实际应用中，课程集与教师集均是大数集，但每位教师所教授的课程仅占课程集中几个元素。这样势必会造成三维有偏权值张量中绝大部分元素为0，即构建的张量是非常稀疏的。

3.2 算法设计

输入：迭代收敛阈值和最大迭代次数max- iteration;

Begin

按教师()-课程()-评分()-权值()构建三维有偏权值张量;

for(=0;< max-iteration;++) {

for each∈[1,2,3] {

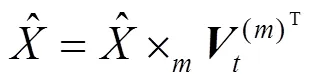
End

4 实验与结果分析

4.1 实验数据集

数据来源于某二本院校4年间728名任课教师、1 683门课程和256 632个真实评价原始记录，实验数据选用了某二级学院40名教师、128门课程以及465个评分(每位教师4年所授课程的学生评分的总平均值按式(9)计算)的记录数据。

设定不同的比重系数、Dw和，得到不同的实验数据集。根据定义3，不同的和Dw对Pbd有影响，表1为=0.7，Dw=0.4时的Pbd值。=0.5，Dw=0.2时，Pbd变化情况如表2所示。

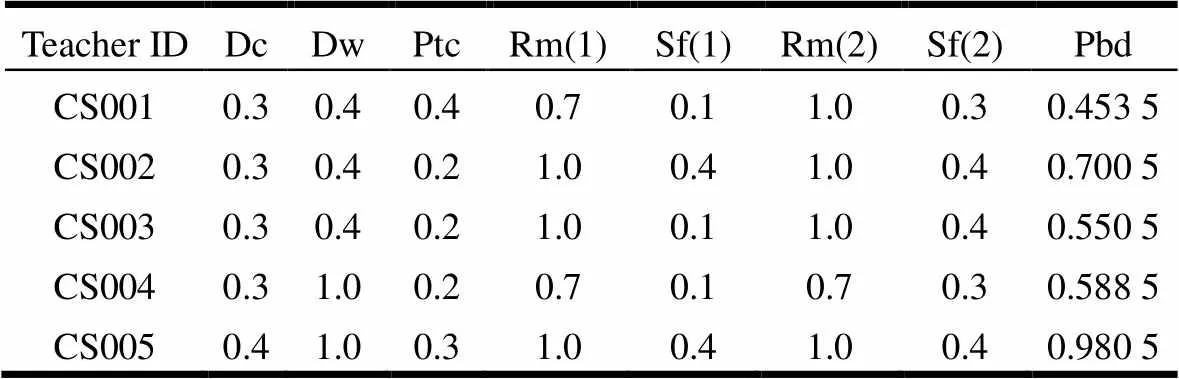
表1 教师信息维表(非全日制)

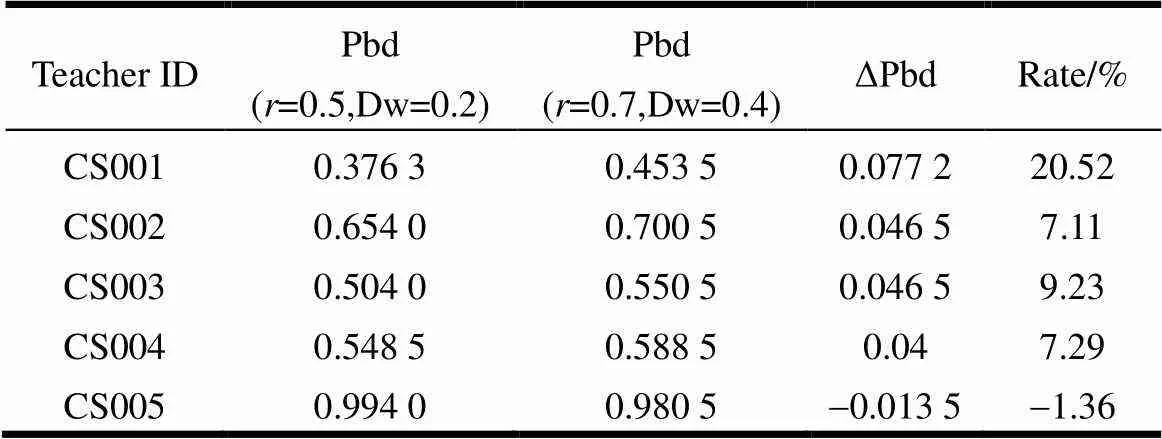
表2 Pbd变化情况

是确认课程难度中教师专家给出的值的比重，根据定义4可以很明显的看出，的变化对课程难度的评定也是有影响的，如表3所示。

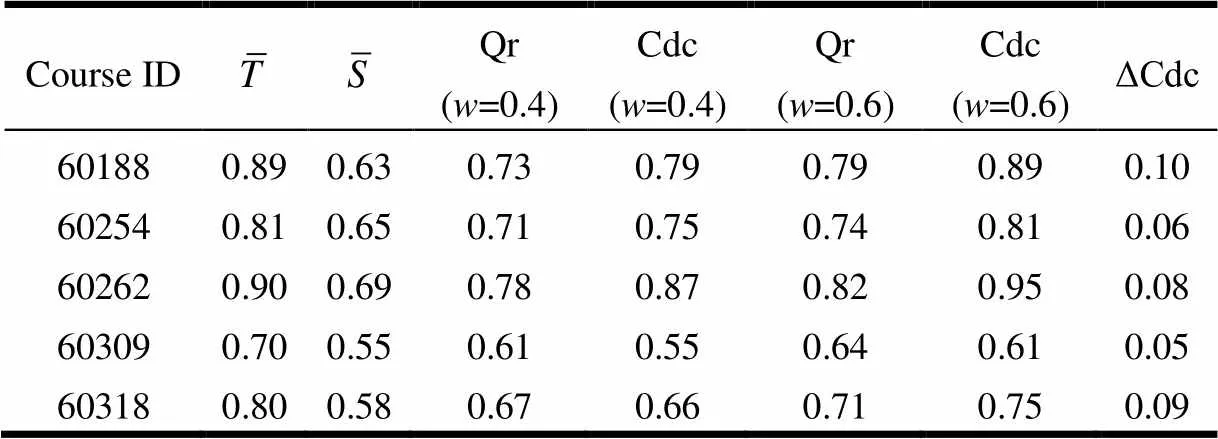
表3 w值对课程难度的影响

课程评价数据Eva按定义5中的式(9)和式(10)可以得到，如表4所示。

表4 学生评分

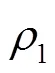
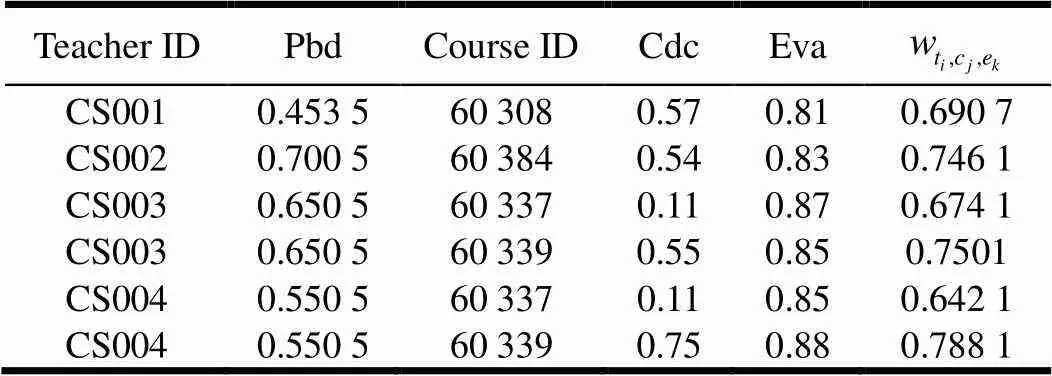
表5 实验数据集(E)

根据表5的实验数据，按有偏权值张量模型构建稀疏程度为90.92%的张量，其非0值元素在三维张量模型中的分布如图2所示。

图2 稀疏有偏权值张量X非零元素分布图

4.2 实验及结果分析

实验1：推荐精度与排序准确性

为了保证每门课程在训练集和测试集中都有数据，在实验数据集中，任选每门课程的20%作为测试集T，在余下的80%实验数据-T中随机选取每门课程的60%、70%、80%、90%和100%作为训练集，进行授课推荐实验。在每个不同比例的训练集上，将迭代收敛阈值分别设为0.005、0.001、0.000 5和0.000 1。

然后采用文献[17]中的平均绝对误差(mean absolute error, MAE)[18]评价指标来衡量各推荐实验的精度，定义如下：

采用P@[19](Precision at)来评价课程的前个被推荐教师的相关性(实验中仅考虑1、3、5这3种值)，该评价指标适合TOP_推荐评测：

经过实验发现，任选E-TE中60%、70%、80%、90%和100%的实验数据作为训练集实验时，不同迭代收敛阈值e下MAE结果如图3所示：

从图中可以看出，使用不同比例训练集的预测精度是不一样的，比例越高，预测精度越好；算法迭代收敛阈值越小，预测精度也越好。实验表明，迭代阈值小于或等于0.000 5，采用上述任一比例训练集，其平均绝对误差MAE均小于1。如果训练集大于余下的实验数据集的90%及以上，迭代阈值Î[0.000 1，0.005]，也可使MAE值小于1，在这些情况下，可认为预测精度达到要求。

固定迭代阈值=0.000 5，训练集任选-T的60%、70%、80%、90%和100%，在取不同时P@排序准确性对比如图4所示：

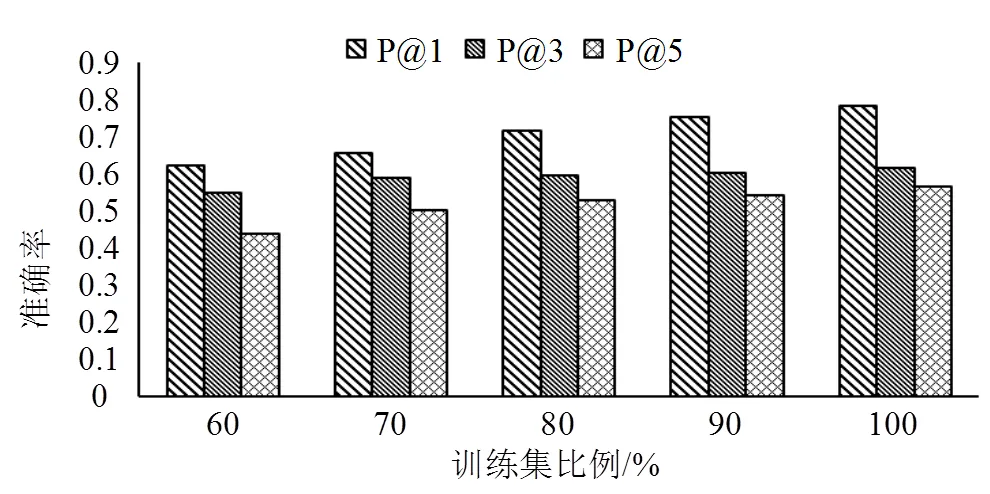
图4 不同比例训练集在不同N下的P@N对比图

从图中可以看出，训练集越大，算法排序准确性越高；值越小，排序准确性相对来说也会越高。

实验2：不同比重系数下的推荐对比

用一系列对比实验检验不同比重系数下的推荐差异，在每组对比实验中，约定从各实验数据集中任选每门课程的20%作为测试集，余下的80%作为训练集，算法迭代阈值=0.000 5，对比在同一门课程下的Top_5的推荐差异：

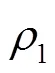
表6 不同r、Dw值下的Top_5推荐对比(Course ID=60 264)

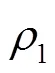
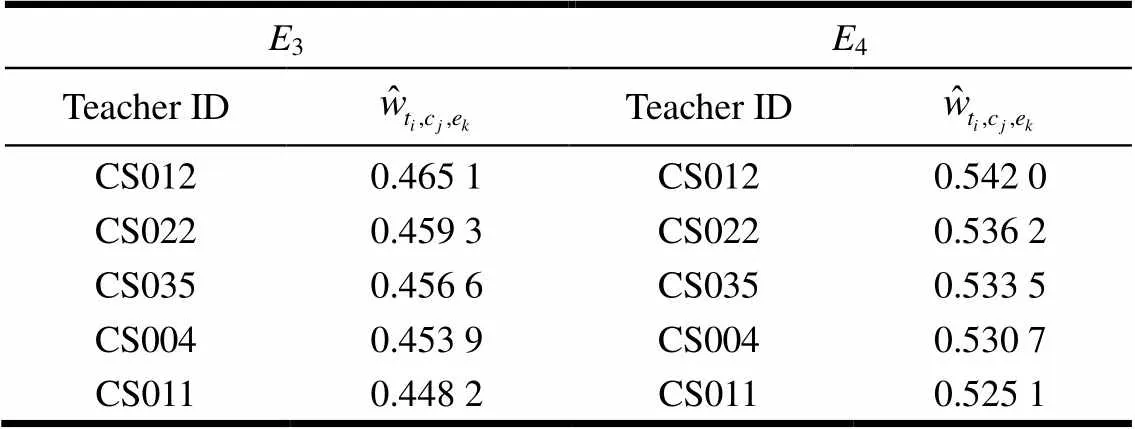
表7 不同w值下的Top_5推荐对比(Course ID=60 264)

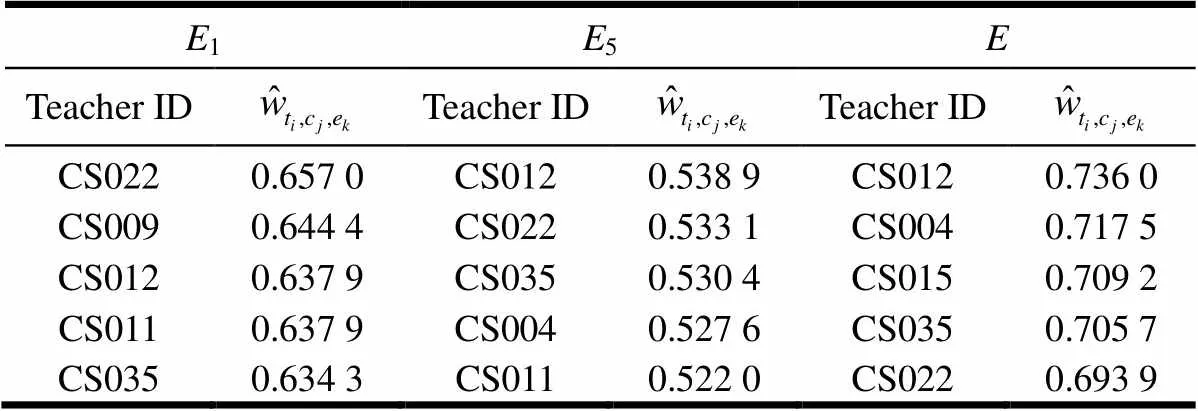
表8 不同偏重系数下的Top_5推荐对比(Course ID=60 264)

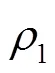
表9 任意比重系数下的Top_5推荐对比(Course ID=60 264)

上述实验表明，采用文中的形式化定义规约教师专业基础度、课程难度和课程评价，取综合有偏权值作为三维加权张量模型元素，使用Tucker分解算法，可按不同侧重点精确实现授课推荐。因此，建议每所学校根据自身需求设定授课推荐依据，选取合适的比重系数，获得较理想的推荐结果，有效地提高教学质量。

5 结束语

从授课安排无较好的推荐依据的实际问题出发，通过归约教师专业基础、课程难度及教学评价，定义具有偏重性的加权方法，构建基于“教师-课程-评价-权值”四元关系之上的三维有偏权值张量模型，使用基于Tucker的分解算法，成功地实现了精准授课推荐，解决了一直以来授课安排无推荐依据的现状，为实现智能化精准授课推荐找到了一种新方法。如何更好地结合教师年龄、职称、专业方向等特征，更进一步精确地和多样化地实现个性化授课推荐，将是下一步研究的重点。

[1] GOLDBERG D, NICHOLS D, OKI B M, et al. Using collaborative filtering to weave an information tapestry[J]. Communications of the ACM, 1992, 35(12): 61-70.

[2] 李聪, 梁昌勇, 马丽. 基于领域最近邻的协同过滤推荐算法[J]. 计算机研究与发展, 2008, 45(9): 1532-1538.

LI Cong, LIANG Chang-yong, MA Li. A collaborative filtering recommendation algorithm based on domain nearest neighbor[J]. Journal of Computer Research and Development, 2008, 45(9): 1532-1538.

[3] 于江德, 李学钰, 樊孝忠, 等. 最大熵模型的事件分类[J]. 电子科技大学学报, 2010, 39(4): 612-616.

YU Jiang-de, LI Xue-yu, FAN Xiao-zhong, et al. Event classification based on maximum entropy model[J]. Journal of University of Electronic Science and Technology of China, 2010, 39(4): 612-616.

[4] 叶茂, 陈勇. 基于分布模型的层次聚类算法[J]. 电子科技大学学报, 2004, 33(2): 171-174.

YE Mao, CHENG Yong. Hierarchical clustering algorithm based on distribution model[J]. Journal of University of Electronic Science and Technology of China, 2004, 33(2): 171-174.

[5] 廖志芳, 李玲, 刘丽敏, 等. 三部图张量分解标签推荐算法[J]. 计算机学报, 2012, 35(12): 2625-2632.

LIAO Zhi-fang, LI Ling, LIU Li-min, et al. A tripartite decomposition of tensor for social tagging[J]. Chinese Journal of Computers, 2012, 35(12): 2625-2632.

[6] 邹本友, 李翠平, 谭力文, 等. 基于用户信任和张量分解的社会网络推荐[J]. 软件学报, 2014, 25(12): 2852-2864.

ZOU Ben-you, LI Cui-ping, TAN Li-wen, et al. Social recommendations based on user trust and tensor factorization[J]. Journal of Software, 2014, 25 (12): 2852- 2864.

[7] 廖志芳, 王超群, 李小庆, 等. 张量分解的标签推荐及新用户标签推荐算法[J]. 小型微型计算机系统, 2013, 34(11): 2472-2476.

LIAO Zhi-fang, WANG Chao-qun, LI Xiao-qing, et al. Tag recommendation and new user tag recommendation algorithms based on tensor decomposition[J]. Journal of Chinese Computer Systems, 2013, 34(11): 2472-2476.

[8] 孙玲芳, 冯遵倡. 基于特征加权张量分解的标签推荐算法研究[J]. 江苏科技大学学报: 自然科学版, 2015, 29(6): 574-579.

SUN Ling-fang, FENG Zun-chang. Tag recommendation algorithm based on feature weighting and tensor decomposition[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2015, 29(6): 574-579.

[9] 孙玲芳, 李烁朋. 基于K-means聚类与张量分解的社会化标签推荐系统研究[J]. 江苏科技大学学报: 自然科学版, 2012, 26(6): 597-601.

SUN Ling-fang, LI Shuo-peng. Social tagging recommendation system based on K-means cluster and tensor decomposition[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2012, 26(6): 597-601.

[10] 张昌利, 龚建国, 闫茂德. 基于复杂网络的社会化标签语义相似度分析[J]. 电子科技大学学报, 2012, 41(5): 642-648.

ZHANG Chang-li, GONG Jian-guo, YAN Mao-de. Complex network based semantic similarity measure for social tagging systems[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(5): 642-648.

[11] SYMEONIDIS P, NANOPOULOS A, MANOLOPOULOS Y. A unified framework for providing recommendations in social tagging systems based on ternary semantic analysis[J]. IEEE Transactions on Knowledge & Data Engineering, 2010, 22(2): 179-192.

[12] SYMEONIDIS P, NANOPOULOS A, MANOLOPOULOS Y. Tag recommendations based on tensor dimensionality reduction[C]//Proceedings of the 2008 ACM Conference on Recommender Systems. New York: ACM, 2008: 43-50.

[13] ADOMAVICIUS G, TUZHILIN A. Toward the next generation of recommender systems: a survey of the state-of-the-art and possible extensions[J]. IEEE Transactions on Knowledge & Data Engineering, 2005, 17(6): 734-749.

[14] BADER B W, KOLDA T G. Tensor decompositions and applications[J]. Siam Review, 2009, 51(3): 455-500.

[15] TUCKER L R. Some mathematical notes on three-mode factor analysis[J]. Psychometrika, 1966, 31(3): 279-311.

[16] 余刚, 王知衍, 邵璐, 等. 基于奇异值分解的个性化评论推荐[J]. 电子科技大学学报, 2015, 44(4): 605-610.

YU Gang, WANG Zhi-yan, SHAO Lu, et al. Singular value decomposition-based personalized review recommendation [J]. Journal of University of Electronic Science and Technology of China, 2015, 44(4): 605-610.

[17] 朱郁筱, 吕琳媛. 推荐系统评价指标综述[J]. 电子科技大学学报, 2012, 41(2): 163-175.

ZHU Yu-xiao, LÜ Lin-yuan. Evaluation metrics for recommender systems[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(2): 163-175.

[18] BREESE J S, HECKERMAN D, KADIE C. Empirical analysis of predictive algorithms for collaborative filtering[C]//Proceedings of the Fourteenth Conference on Uncertainty in Artificial Intelligence. Madison, USA: ACM, 1998: 43-52.

[19] WANG L, MENG X, ZHANG Y, et al. New approaches to mood-based hybrid collaborative filtering[C]//The Workshop on Context-Aware Movie Recommendation. Barcelona: ACM, 2010: 28-33.

编 辑 叶 芳

A Three-Dimensional Partial Weight Tensor Model for Teaching Recommendation

YAO Dun-hong1,2, LI Shi-jun2, and HU Ya-hui2,3

(1. College of Computer Science & Engineering, Huaihua University Huaihua Hunan 418000; 2. School of Computer, Wuhan University Wuhan 430072; 3.The Fourth Department of Air Force Early Warning Academy Wuhan 430010)

To address the problem that the teaching arrangements are not on the basis of recommendation in current school, a series of formalized methods are used to specify teachers’ specialty foundation, course difficulty, and teaching evaluation first. Then, a kind of weighted function is defined to calculate the comprehensive partial weight for each group of teachers’ professional foundation, course difficulty, and teaching evaluation. Next, the three-dimensional tensor model with partial weight is built on the 4-tuples relation of teacher-course- evaluation-weight and the comprehensive weight is endowed to the tensor elements. Finally, on the basis of above，a new kind of decomposition algorithm based on Tucker Decomposition is designed to obtain the approximate tensor of dimensionality reduction with the higher-order singular value decomposition (HOSVD), achieving the Top-recommendation of teaching arrangements. Experiment results show that our proposed method can realize precise teaching arrangements recommendations when the iterative threshold value reaches a reasonable value, which can be used as a new intelligent recommendation method applied to the teaching arrangements in all kinds of schools.

data reduction; teaching recommendation; tensor decomposition; three-dimensional partial weighted tensor

TP391

A

10.3969/j.issn.1001-0548.2017.05.018

2016-03-17；

2017-05-05

国家自然科学基金(61272109)；湖南省教育厅科学研究项目(15C1086)

姚敦红(1972-)，男，副教授，主要从事数据挖掘、机器学习方面的研究.