高中数学作业结构调整的尝试
李建辉

中图分类号:G633.6 文献标识码:B文章编号:1672-1578(2017)09-0155-02
2011年起我们课题组以主动作业为主题,进行了许多有益的探索,形成了一些较典型和生动的高中数学作业新模式。
1.自选作业
做法:教师按教学单元提供大量的数学巩固性作业,教师只提一个每天完成作业的最低量的要求,让学生自由选择完成。
特色与优势:尊重了学生的选择,改善了作业效果,学生享受到了做作业的主人的快乐。
2.分层矫正作业
做法:教师在一个教学单元结束时进行"形成性测验",根据测验结果将学生分成"合格"和"需努力"两个层次。教师提供矫正作业,要求"需努力"的学生独立完成后交给"合格"的学生批改讲评。
特色与优势:班级授课制下学生的学习结果不会整齐划一的,教师不在教学单元开始时将学生进行层次划分,而在教学单元结束时划分。这样做有利于学生在教学单元的学习过程中学会自主选择作业。而矫正作业的分层次要求,有利于形成互帮互助的学习风气。提高学生完成作业的主动性和积极性。
以上两种作业模式均属于巩固性作业,以巩固"双基"为目的。
3.研究性作业
做法:①教师给定范围或专题,学生选题;②学生搜集整理资料;③反馈与修正;④形成作业成果;⑤汇报交流,进行评价。
特色与优势:教师给定范围,学生有更大的选择自由,完成时空跨度大,可以寻求合作伙伴,有创造性,与生活紧密结合,加速了个体的社会化,可以培养学生信息利用等能力。与传统作业比较,探索研究性作业有明显的优势:⑴探索研究性作业往往是综合的专题学习,学生在驾驭专题学习中容易成为学习活动的主人,有利于学生创新思维与能力的培养;⑵作业完成时间较长,作业反馈相应延迟,时空的广阔,有利于提高学生学习的自觉性,提高学生广泛搜集信息的意识和能力;⑶重视从单独完成到合作完成,有利于培养学生的合作精神;⑷作业过程、完成方式和评价方式等方面的开放性。
研究性作业是对传统作业的结构性调整,针对传统作业的弊端:"问题的提出是课本和教师;数据的提供是课本和教师;解答的外开放性;作业形式单一;作业不鼓励合作;重视结果而不重视过程;对作业的评价是被动评价。"而设计的作业模式。我们借鉴英特尔?未来教育理念,为学生提供与学习内容紧密相关的研究课题,学生带着问题,边学习,边研究,提高了数学学习的层次,把自己的研究成果与同学交流、共享,增强了学生学习数学的兴趣和信念,合作意识和创新精神也得到了培养。
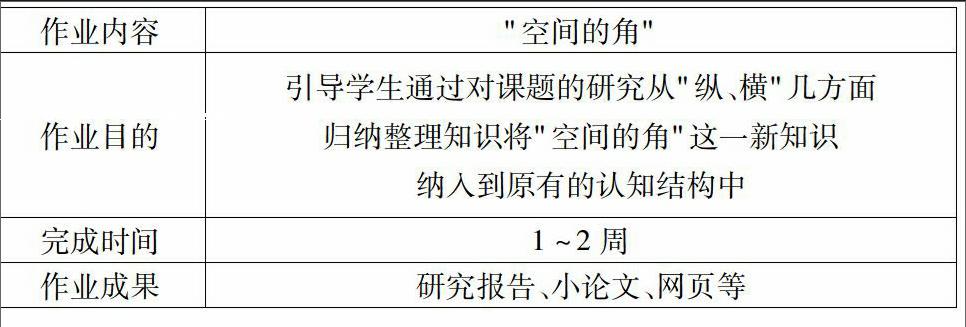
如,立体几何(华师大版《数学》第八章学完后,我们为学生提供了下面一个作业:
通过1~2周的饶有兴趣认真的合作研究,硕果累累,《试论空间角规定的合理性》、《异面直线所成角的确定方法》、《"擎天柱"与二面角的平面角的寻找方法》等等。通过交流,分享,同学们说我们对"空间的角"有了更深的认识。"空间的角"作业摘录如下:
"角是一个平面概念。空间的线线、线面、面面也会有角的形象,如直线与平面相交时就给我们以角的形象,但为什么要规定直线与该直线在这个平面内的射影所成的锐角为直线和平面所成的角呢?……"
"确定异面直线所成角的方法通常有两种方法。一、运用中位线定理,二、运用平行四边形。
例一:正三棱锥S-ABC中E、F分别是AB、SC的中点。设侧棱和底面边长都是a,求異面直线SE与BE所成的角的大小。
【分析】本题取EC的中点G,利用中位线定理可得∠GFB就是异面直线SE与BE所成的角。解三角形GFB即可得∠GFB=arccos23。
"求二面角的大小关键确定二面角的平面角我们研究发现如下图是确定二面角的平面角的一种最常用的方法,我们把线段PQ称为"擎天柱"因为有了它二面角的平面角就可有三垂线定理得到了。……"
……
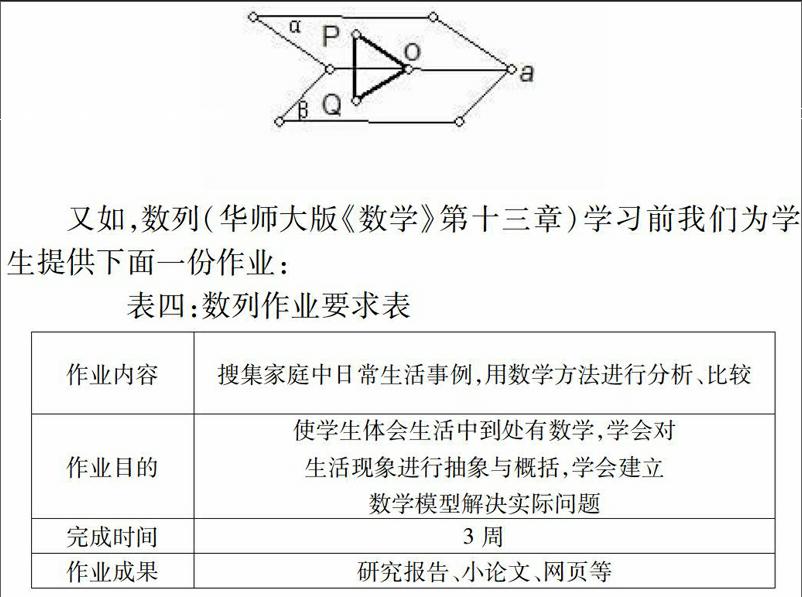
又如,数列(华师大版《数学》第十三章)学习前我们为学生提供下面一份作业:
3周后,同学们在成果交流会上,交流了《买那家的电视机合算》、《按揭贷款购房研究》、《家庭理财研究》等等研究成果。同学们说原来生活中处处有数学。
高中数学作业结构中应包含巩固性作业和研究性作业。巩固性作业主要是落实单元教学的知识目标,巩固基本知识和基本技能。培养学生的演绎、归纳的思维能力、运算能力和空间想象能力,培养学生的公理化与结构思想、函数思想及转化思想等数学思想方法。研究性作业是研究性学习的材料,主要是让学生学会搜集信息、处理数据、制作图表、分析原因、推出结论来解决实际问题的方法。学会把实际问题归结为数学模型,然后运用数学方法进行探索、猜测、判断、论证、运算、检验,使问题得以解决。学会使用数学语言表达和交流。培养学生实事求是的科学态度,顽强的学习毅力和独立思考、探索创新的精神和合作交流意识。
新型的高中数学作业结构在我校高二年级的数学教学的实践表明:新型的高中数学作业结构中不仅仅是知识的巩固和运用,还反映出学生智能结构的发展。我们的探索仅是一个开始,我们还将不断探索和实践。endprint

