Flow patterns and critical criteria of thermally strati fied shear flow in braided rivers

Li Gu*,Qiu-lan Li,Bo Dai,Zu-lin Hua,Xiao-ong Liu,K-jian Chu

aDepartment of Civil and Environmental Engineering,University of Alberta,Edmonton T6G 2R3,Canada bKey Laboratory of Integrated Regulation and Resource Development of Shallow Lakes,Ministry of Education,Hohai University,Nanjing 210098,China cZhenjiang Urban Planning and Design Institute,Zhenjiang 212000,China dJiangsu Transportation Institute,Nanjing 210098,China eNational Engineering Research Center of Water Resources Ef ficient Utilization and Engineering Safety,Hohai University,Nanjing 210098,China

Received 7 August 2016;accepted 12 May 2017 Available online 6 October 2017

Flow patterns and critical criteria of thermally strati fied shear flow in braided rivers

Li Gua,b,*,Qiu-lan Lic,Bo Daid,Zu-lin Huab,Xiao-dong Liue,Ke-jian Chue

aDepartment of Civil and Environmental Engineering,University of Alberta,Edmonton T6G 2R3,CanadabKey Laboratory of Integrated Regulation and Resource Development of Shallow Lakes,Ministry of Education,Hohai University,Nanjing 210098,ChinacZhenjiang Urban Planning and Design Institute,Zhenjiang 212000,ChinadJiangsu Transportation Institute,Nanjing 210098,ChinaeNational Engineering Research Center of Water Resources Ef ficient Utilization and Engineering Safety,Hohai University,Nanjing 210098,China

Received 7 August 2016;accepted 12 May 2017 Available online 6 October 2017

Flow characteristics of thermally strati fied shear flow in braided rivers are particularly complicated and poorly understood.In this study,a series of typical flow patterns was examined and their critical criteria were determined.Four flow patterns were identi fied:mixed,locally unstable,continuously strati fied,and two-layer flow.Temperature distributions of the four types of flow patterns were analyzed and compared.The critical Froude numbers for unstable flow,FDcr1,and stable flow,FDcr2,were determined to be 6 and 1,respectively,and comparison of FDcr1and FDcr2to the peak Froude numbers,FD1at the outer bank and FD2at the inner bank along the anabranch,allowed the flow patterns to be assessed.Then,a discriminant based on initial Jeffreys-Keulegan stability parameters was established to distinguish the flow stages from twolayer flow to completely mixed flow.It is indicated that the three critical Jeffreys-Keulegan parameters increased with the diversion angle of braided rivers.Results also show that,compared to the strati fied flow in straight and curved channels,it was more dif ficult for braided strati fied flow to maintain as two-layer flow,and it more easily became mixed flow.Consequently,empirical expressions for stability criteria of the thermally strati fied shear flow in braided rivers are presented.

©2017 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Braided river;Critical criterion;Empirical formula;Flow pattern;Temperature distribution;Thermally strati fied flow

1.Introduction

When a vertical density gradient is maintained along a stream,and the density remains strati fied throughout the channel,the flow is considered stable strati fied.Otherwise,it is considered mixed flow.Within stable strati fied flow,thereis an extreme state,i.e.,two-layer flow,where matter and energy exchanges rarely occur between the upper and lower fluids.

Strati fied flow in single straight or curved channels has been ■widely studied(Donda et al.,2015;García-Villalba and DelAlamo,2011;Huai et al.,2010;Schiller and Sayre,1975;Schmid et al.,2004;Williamson et al.,2015;Zeng and Huai,2005).The flow structure and temperature distribution of strati fied flow in a single channel are relatively simple compared to those in braided rivers.The hydraulic phenomena in the case when strati fied flow passes through a braided river are complex,and have been studied little,aside from some research on the homogeneous flow structure of braided rivers(Gu et al.,2014,2015;Hua et al.,2009;Richardson and Thorne,1998,2001;Yu et al.,2007).Hua et al.(2009)conducted physical model experiments on homogeneous flow in a typical braided river,and they observed two circulation cells of opposite rotation and a separation zone occurring near the outside wall in the entrance region of the anabranch.Gu et al.(2015)investigated flow structures of strati fied flow in a braided river with three discharges experimentally.However,strati fied flow patterns for different diversion angles and in flow ratios have not been systematically studied.

Research on stability criteria,in the form of dimensionless parameters,such as the Jeffreys-Keulegan stability parameter,Richardson number,and densimetric Froude number,has mainly focused on single channel cases.Keulegan(1949)experimentally investigated the stability of two-layer viscous strati fied flow.Following Jeffreys(1925),Keulegan(1949)derived the Jeffreys-Keulegan stability parameter as follows:

where ν is the kinematic viscosity,g is the gravitational acceleration,ρuis the fluid density of upper light flow,Δρ is the density difference across the interface,and V is the velocity of upper light flow.

Keulegan(1949)found that if the Reynolds number of the upper fluid was less than 450,for two-layer flow the critical Θ was 0.127.Otherwise,the critical Θ was 0.178,which meant that the critical Θ depended on fluid viscosity as well as the turbulent state between the two fluids.Sherekov et al.(1971)determined the critical Θ for each stage from two-layer flow to completely mixed flow,with Θ＞0.188 for two-layer flow and Θ＜0.085 for completely mixed flow.Hua and Chu(2008)conducted a large number of physical experiments in straight and curved channels with different diversion angles to explore the critical initial Jeffreys-Keulegan stability parameters,Θ0cr1and Θ0cr2(for mixed flow,the initial Jeffreys-Keulegan stability parameter Θ0is smaller than Θ0cr1,and for two-layer strati fied flow, Θ0is greater than Θ0cr2),and found that,for straightand curved channels of45°,90°,and 180°,Θ0cr1=0.04,0.05,0.06,and 0.07,and Θ0cr2=0.06,0.07,0.08,and 0.09,respectively.

Many investigators have contributed to our understanding of the stability conditions of strati fied flow using the Richardson number(Drazin,1958;Galperin et al.,2007;Miles,1961;Rohr and Van Atta,1987;Taylor,1931)and densimetric Froude number(Chu et al.,2008;Harleman,1961;Jin and Zhang,1992;Schiller and Sayre,1975).Thus,the stability properties of strati fied flow in straight and curved channels are understood,and corresponding stability criteria are available.However,the unstable state of strati fied shear flow through braided rivers,a common natural river pattern,remains unclear.Some special and unknown unstable processes of strati fied flow occur due to the suddenly increased cross-section at the bifurcation,the subsequent separation,and the streamline curve along each anabranch.Therefore,it is necessary to examine each stage from two-layer flow to completely mixed flow in braided rivers and explore the stability characteristics and criteria,as a requirement for the study of strati fied flow.

In this study, flow patterns of thermally strati fied shear flow in braided rivers with different diversion angles were explored,and corresponding relationships between stability criteria and the diversion angle were derived.

2.Model of strati fied flow in braided rivers

2.1.Experimental setup

The physical model of a symmetrical braided river with a middle bar that had a diversion angle of 90°is shown in Fig.1.Two independent in flow systems,cold and warm water,were used to generate the thermally strati fied flow.The flume consisted of a straight introduction segment(5 m long),braided segment(1.71 m long),and straight ef fluent segment(5 m long).Symmetrical anabranches 1 and 2 were separated by the middle bar,and L1 through L9 and R1 through R9 were typical cross-sections for analysis in anabranches 1 and 2,respectively.The bank near the middle bar was the inner bank,while the other was the outer bank.The widths of the straight segment and anabranches 1 and 2 were B0,B1,and B2,with B0=0.28 m,and B1=B2=0.2 m.A thin glass plate was set in the straight introduction segment at a height 0.15 m from the bottom to separate the upper(warm)and lower(cold)water.The depths of the warm and cold water were H1and H2,with H1=0.04 m and H2=0.15 m.The total water depth,H,was the sum of H1,H2,and the thickness of the middle glass plate,with H=0.193 m.Temperatures and flow rates in the upper and lower layers are denoted as T1,T2,Q1,and Q2,respectively.The temperature difference was set to 10°C.Velocity and temperature were measured with a Sontek threecomponent acoustic Doppler velocimeter and a digital thermometer,respectively.Other details of the experimental setup with a 90°diversion angle accorded with Li(2014)and Gu et al.(2015).

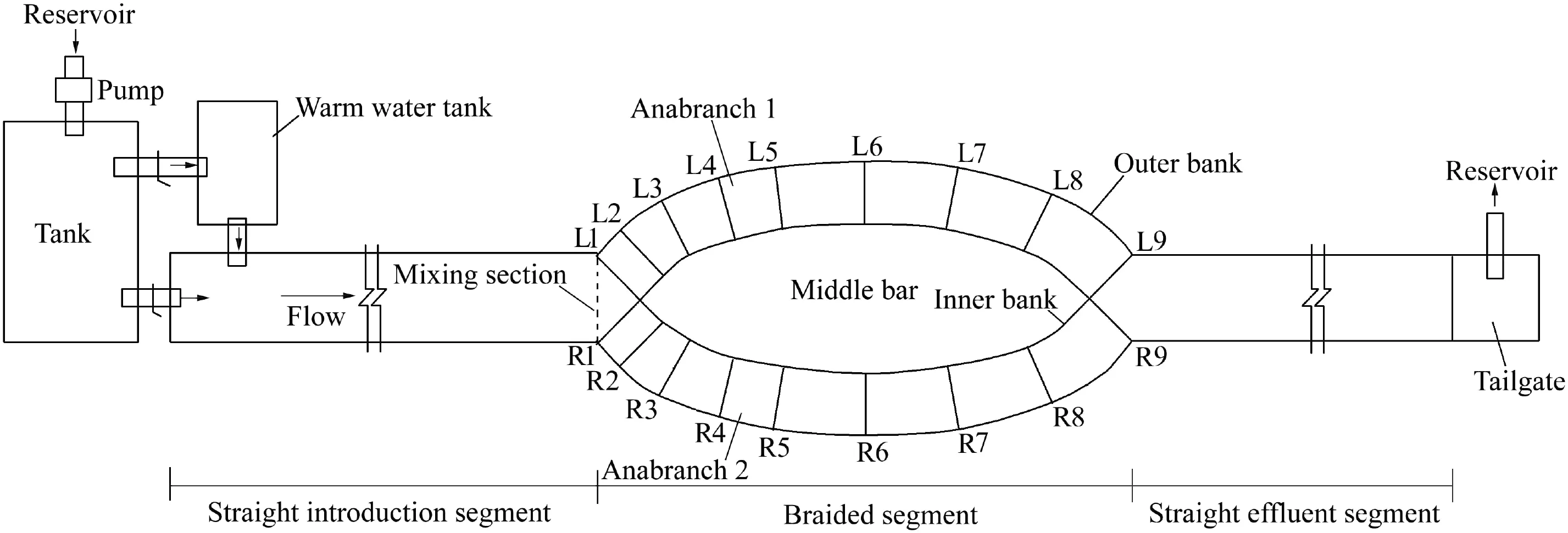
Fig.1.Sketch of braided river model.

2.2.Simulation conditions

Based on measurements from the physical model,a mathematical model,established and veri fied by Li(2014)and Wang(2015),was used to explore flow properties under a variety of conditions.Parameters of flow conditions are listed in Table 1,where θ is the diversion angle of the braided river;V1/V2is the velocity ratio of the upper and lower layers at the inlet;Vmis the overall mean inlet velocity;and Re is the mean Reynolds number,with Re=VmR/ν,where R is the hydraulic radius.The initial Jeffreys-Keulegan stability parameter is

where ρ1and ρ2are the fluid densities at the inlet of the upper and lower layers,respectively.

2.3.Governing equations and computational details

A three-dimensionalsecond-momentReynoldsstress model was established and used to simulate the strati fied flow in a braided river.The governing equations in tensor form are as follows:

where U is the time-averaged velocity;u is the fluctuating velocity;p is the static pressure;μ is the dynamic viscosity;βis the volume expansion coef ficient;k is turbulence kinetic energy;ε is the turbulence dissipation rate;T is the timeaveraged thermodynamic temperature(K);φ is the fluctuating temperature;t is time;the subscripts i,j,and l represent the directions of coordinate axes;ρ is the fluid density,with

Table 1 Flow conditions.

No-slip boundaries were applied at all sidewalls and the channel floor.The inlet boundary condition was determined by the measured velocity from experiments,and the outlet boundary condition was set as free flow.The top surface was speci fied as symmetry.The channel floor roughness was set as 0.009 for a smooth organic glass bottom.

Fig.2.Local computational meshes.

The simulation domain was divided into three segments:an upstream straight segment,a downstream straight segment,and a braided segment,as shown in Fig.1.The two straight segments were geometrically simple,and a structural mesh was generated,with the length,width,and height of each element being 0.1 m,0.01 m,and 0.01 m,respectively.Due to the complicated geometry of the braided segment,an unstructured and re fined mesh was generated(Fig.2).Moreover,meshes at the bed and the interface between warm water and cold water were also re fined.The simulation domain was divided into 480000 elements.

The experimental results in case 4 were used to validate the numerical predictions.Figs.3 and 4 illustrate the comparison of measured and calculated longitudinal velocity and temperature distributions at the outer bank,centerline,and inner bank in some typical cross-sections.The dimensionless velocity u*is non-dimensionalized by the overall mean inlet velocity Vm;and T*is the relative temperature increase,with T*= （T-T2）/（T1-T2）,where T1and T2are the temperatures of the upper and lower layers.z is the non-dimensionalized depth,with z=h/B0,where h is the water depth.As demonstrated in the figures,the velocity pro files and temperature distributions of the model simulation and experimental measurements show strong agreement.The mean absolute percentage errors(MAPEs)of the dimensionless velocity and relative temperature increase were less than 10%and 15%,respectively,which were considered reasonable for model prediction.

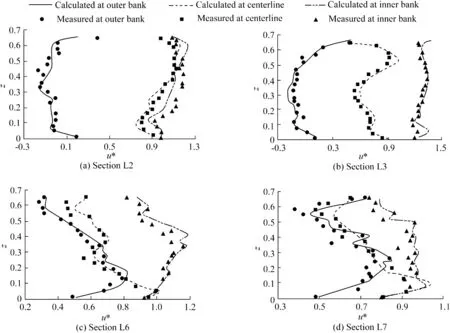
Fig.3.Comparison of measured and calculated longitudinal velocity distributions at outer bank,centerline,and inner bank in different sections in case 4.

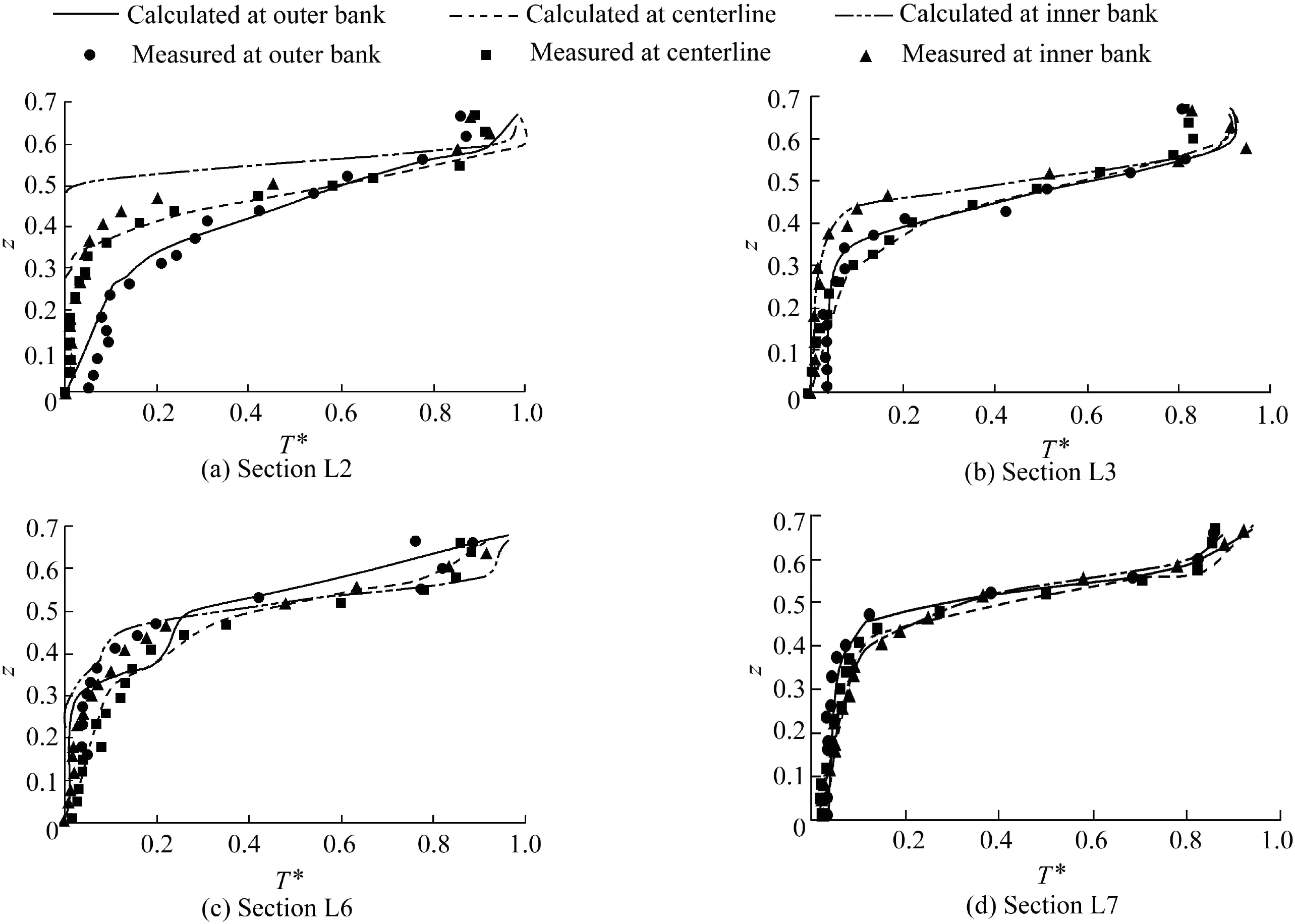
Fig.4.Comparison of measured and calculated distributions of relative temperature increase at outer bank,centerline,and inner bank in different sections in case 4.

3.Flow patterns and stability analysis

Simulation results from the model with the diversion angle of 30°showed that three typical flow patterns occurred with decreasing Θ0,as shown in Fig.5.In order to identify the typical characteristics and stability of different flow patterns,the densimetric Froude numbers of the vertical cross-sections were calculated.The densimetric Froude number is de fined as whereis the mean velocity of the cross-section,and ρsis the mean density of the surface layer warm water in the vertical pro file.

Fig.6 shows the relationship between FDand the relative distance xrel=s/H in anabranch 1,where s is the distance from the first section along the centerline of the anabranch.

The flow pattern in Fig.5(a)shows that the surface was always covered by warm water along the anabranch,the temperature gradient in the vertical direction was large,and there was a temperature gradient jump at the interface between cold water and warm water,where matter and energy exchanges were very few.Values of FDat the outer bank,centerline,and inner bank of each cross-section along the anabranch in this flow pattern were small and all below 0.8(Fig.6(a)).

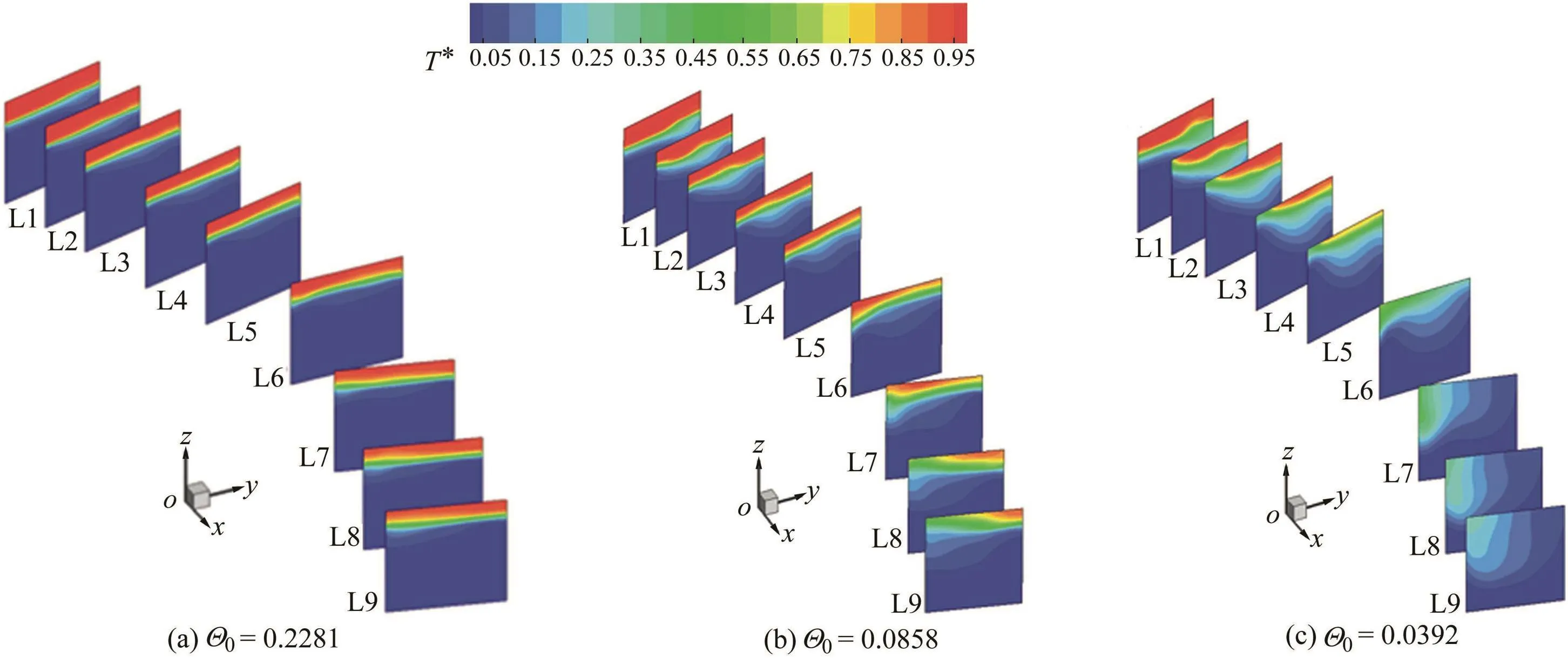
Fig.5.Dimensionless temperature contours of typical flow pattern in 30°model.

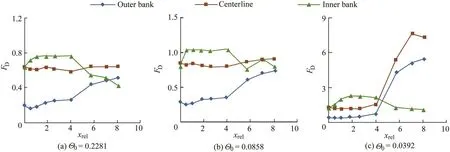
Fig.6.FDdistributions at outer bank,centerline,and inner bank for typical flow patterns in 30°model.

The flow pattern in Fig.5(b)shows that the surface was covered by warm water,a transition layer occurred between the cold and warm water layers,and the temperature gradient was relatively small.In this flow pattern,FDfluctuated at the inner bank along the anabranch,with the peak FDoccurring in the first half of the anabranch,whose value was a little greater than 1(Fig.6(b)).

The flow pattern in Fig.5(c)shows that signi ficant mixing between cold and warm water occurred in the latter half of the anabranch and in the exit section(L9)of the anabranch,and the outer bank was totally occupied by cold water.FDat the outer bank and centerline increased along the anabranch,and the peak FDat the outer bank occurred in the exit section L9(Fig.6(c)).

There were similarities in typical flow patterns,but also differences between models with different diversion angles.Simulation results of models with diversion angles of 45°,60°,75°,and 90°showed additional flow patterns to the previous three typical patterns.With the 90°model as an example(Fig.7),different flow patterns occurred in different cases.In the flow pattern shown in Fig.7(c),only a local region near the inner bank in the first half of the anabranch was occupied by cold water,and the remainder of the surface was covered by warm water.This is due to a secondary current pushing the cold water at the inner bank in the first half of the anabranch upward,causing instability.According to the variation of FDalong anabranch 1(Fig.8),the peak FDat the inner bank always occurred in the first half of the anabranch.Moreover,the peak FDat the outer bank occurred in the exit section L9.

The contours of dimensionless longitudinal velocity,u*,temperature,T*,turbulence kinetic energy,k*,and turbulence viscosityalong anabranch 1 in case 3 are shown in Fig.9.k*andwere normalized by the square of Vmand the maximum value of νt,respectively.High-turbulence zones occurred in the transition region between the high-and lowvelocity zones.

Thus,it can be inferred that a large FDvalue occurs with unstable flow,and a small FDvalue corresponds to stable flow.In addition,the peak FDat the outer bank along the anabranch almost occurs in the outlet section,and the peak FDat the inner bank occurs in the first half of the anabranch.Some key parameters are de fined as follows:

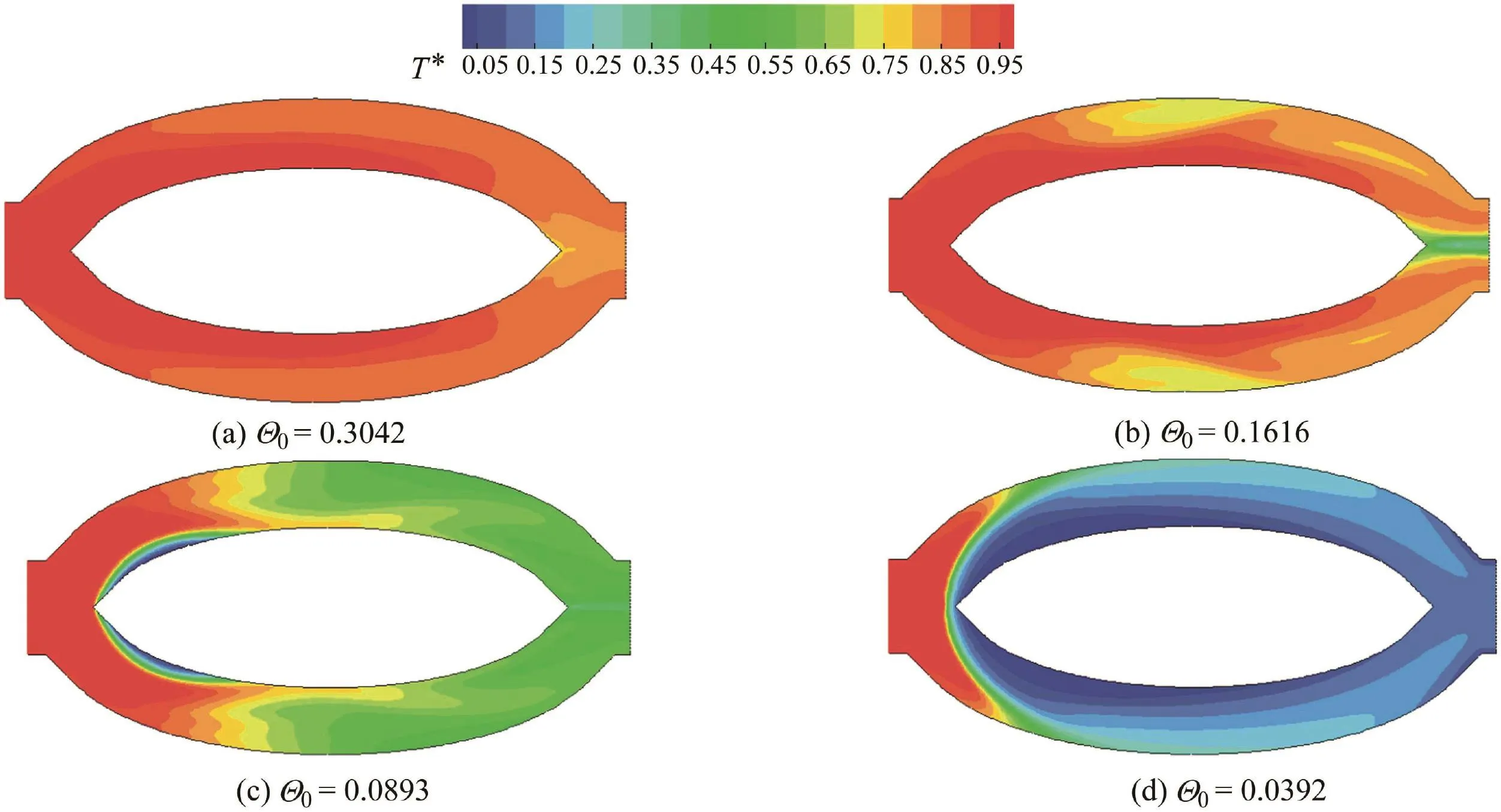
Fig.7.Dimensionless temperature contours of typical flow patterns in 90°model.

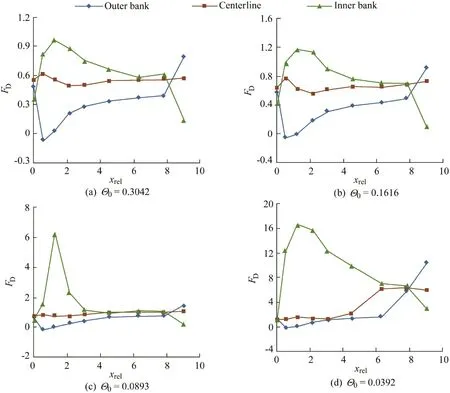
Fig.8.FDdistributions at outer bank,centerline,and inner bank for typical flow patterns in 90°model.

FDcr1is the critical value of FDfor unstable flow,such that when FD＞FDcr1,strati fied flow becomes unstable.FDcr2is the critical value of FDfor two-layer flow,such that when FD＜FDcr2,strati fied flow exhibits the two-layer flow pattern.FD1and FD2are the peak FDat the outer and inner banks along the anabranch,respectively.

In order to obtain values of FDcr1and FDcr2,relationships between FDand xrelat the outer bank and inner bank with different diversion angles for different initial Jeffreys-Keulegan stability parameters are analyzed,as shown in Fig.10.

From the flow patterns generated by numerical simulation and physical experiments,it was found that in the local zone with FD＜1,the interface was stable and two-layer flow could maintain.Meanwhile,in the local zone with FD＞6,the strati fied flow was unstable and water was mixed violently.Consequently,FDcr1=6,and FDcr2=1.Similar results were found by Chu et al.(2004).

Thus,through combinations of FDdistributions at the inner and outer banks(Fig.10)and simulated flow patterns,the following could be determined:

(1)When FD1＜1 and FD2＜1,two-layer flow occurred,in which there was marked interface and little flow exchange between the two layers.

(2)When FD1＞6,regardless of the value of FD2,mixed flow occurred,in which the interface at the outlet section had been completely destroyed.

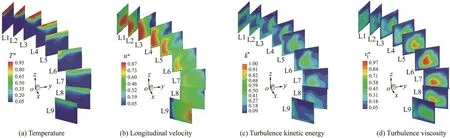
Fig.9.Dimensionless temperature,longitudinal velocity,kinetic energy,and turbulence viscosity distributions along anabranch 1 in case 3.

Fig.10.Variations of FDat outer bank and inner bank along anabranch 1 for braided river model with different diversion angles.

(3)When FD1＜6 and FD2＞6,locally unstable flow occurred,in which the unstable zone was only located at the inner bank in the first half of the anabranch.

(4)When FD1＜6 and 1＜FD2＜6,continuously strati fied flow occurred,in which a transition layer forms between the cold and warm water layers.

Thus,the flowpatternscanbeassessedthroughthevalueofFDfor braided rivers.However,the vertical distributions of fluid density and velocity along the anabranch must be measured,whichisatime-consumingandlabor-intensiveprocess.Notethat the flow patterns of strati fied flow are related to Θ0,which is determinedbytheinletvelocitiesandtemperaturesoftwolayers,and can be obtained more easily than FDalong the anabranch.Therefore,relationshipsbetween flowpatternsandcriticalΘ0for braided river models with different diversion angles should be established.Fig.11 shows the relationships between FD1,FD2,andΘ0,which can beusedtoobtainthecriticalΘ0.Notethatthe correlationbetweenthepeakFDandΘ0isnegative.Thus,simple and universal discriminants for flow patterns in braided rivers,namely,stability criteria,can be obtained.

Three critical values were de fined to distinguish different flow patterns: Θ0cr1is a value of Θ0corresponding to FD1=FDcr1in Fig.11(a),and Θ0cr2and Θ0cr3are values of Θ0corresponding to FD2=FDcr1and FD2=FDcr2,respectively,in Fig.11(b).Corresponding stability criteria are as follows:

(1) Mixed flow occurred when Θ0＜Θ0cr1, since FD1＞FDcr1.Θ0cr1=0.0354,0.0421,0.0457,0.0522,and 0.0613,respectively,for the 30°,45°,60°,75°,and 90°models.

(2)Locally unstable flow occurred when Θ0cr1＜ Θ0＜ Θ0cr2,since FD2＞FDcr1and FD1＜FDcr1.The strati fied flow was unstable at the inner bank and stable at the outer bank.Θ0cr2=0.0323,0.0423,0.0538,0.0777,and 0.0935,respectively,for the 30°,45°,60°,75°,and 90°models.Note that Θ0cr1=0.0354 for the 30°model,which means that the locally unstable flow pattern could not occur for this model,and flow remained mixed.Thus,Θ0cr2did not exist in the 30°model.Therefore,when Θ0cr2＜ Θ0cr1,irrational Θ0cr2values may be ignored.

(3)Two-layer flow occurred when Θ0＞Θ0cr3,since FD2＜FDcr2and FD1was always less than FD2at this time.Θ0cr3=0.1056,0.1115,0.1321,0.2501,and 0.2840,respectively,for the 30°,45°,60°,75°,and 90°models.

(4)Continuously strati fied flow occurred when Θ0cr2＜Θ0＜Θ0cr3.

The relationships between the critical initial Jeffreys-Keulegan stability parameter and diversion angle of braided river models were obtained:

Generally,their relationships were positive:the critical initial Jeffreys-Keulegan stability parameter increases with the diversion angle.

4.Discussion

V in Eq.(1)is actually the velocity difference between two layers due to the velocity of the lower heavy water being set to zero.Hua and Chu(2008)used the mean velocity of the crosssection to calculate the Jeffreys-Keulegan stability parameter Θ for the straight and curved channels with different diversion angles.For comparison,the velocity difference between two layers was calculated according to their experimental conditions,and the Jeffreys-Keulegan stability parameter was recalculated.It was found that,for the straight and curved channels with the diversion angle of 45°,90°,and 180°,mixed flow occurred when Θ0＜ Θ0cr1,with Θ0cr1=0.049,0.072,0.092,and 0.134,respectively,and two-layer strati fied flow occurred when Θ0＞ Θ0cr2,with Θ0cr2=0.097,0.124,0.171,and 0.250,respectively.

Fig.11.Relationships between FD1,FD2,and Θ0for braided river model with different diversion angles.

In this study,for braided strati fied flow with diversion angles of 30°,45°,60°,75°,and 90°,mixed flow occurred when Θ0＜Θ0cr1,with Θ0cr1=0.0354,0.0421,0.0457,0.0522,and 0.0613,respectively,and two-layer strati fied flow occurred when Θ0＞ Θ0cr3,with Θ0cr3=0.1056,0.1115,0.1321,0.2501,and 0.2840,respectively.There was a very large difference in the experimental conditions between this braided strati fied flow and the strati fied flow of Keulegan(1949),Sherekov et al.(1971),and Hua and Chu(2008).The difference made the critical Jeffreys-Keulegan parameter values hard to compare directly.However,it was found that the critical Jeffreys-Keulegan parameters increased with the diversion angle both in this study and in that of Hua and Chu(2008).Moreover,it seemed that,for braided strati fied flow,two-layer flow was more dif ficult to maintain,and flow more easily became mixed,as compared to the strati fied flow in straight and curved channels.

Moreover,the water depth of the lower layer in the braided strati fied flow was set at 0.15 m.This depth was considered to be suf ficient because,for stable strati fied flow,the interface thickness was about 2 cm just below the upper light layer(Chu,2006),and the bottom friction and shear could not infl uence the interface.Moreover,from the results of physical experiments(Gu et al.,2015)and numerical simulation in all cases,warm water from the upper layer was not found to move to the bottom in the anabranch before the strati fied flow became completely mixed.

5.Conclusions

The evolution from two-layer flow to completely mixed flow was systematically examined for a braided river.The densimetric Froude number FDwas calculated for each crosssection in the braided river with different diversion angles to identify typical flow patterns.

The peak FDat the inner bank always occurred in the first half of the anabranch for continuously strati fied and two-layer flow,and sharply increased for locally unstable flow.In contrast,mixed flow showed high FDvalues at the outer bank in the secondary half of the anabranch,and the peak FDoccurred in the exit section.

The critical Froude numbers for unstable flow,FDcr1,and two-layer flow,FDcr2,were found to be 6 and 1,respectively.Peak values FD1at the outer bank and FD2at the inner bank were compared with FDcr1and FDcr2,and four distinct flow patternsweredistinguished:two-layer,locally unstable,continuously strati fied,and mixed flow.Locally unstable flow occurred in the 45°,60°,75°,and 90°models,but did not occur in the 30°model.Moreover,compared to the strati fied flow in straight and curved channels,it was more dif ficult for braided strati fied flow to maintain as two-layer flow,and it more easily became mixed flow.

The critical initial Jeffreys-Keulegan stability parameter is more easily obtained than FD1and FD2.Three critical parameters for distinguishing the four flow patterns were determined,and empirical formulas for the relationship between the criticalinitialJeffreys-Keulegan stability parameterand diversion angle θ of the braided river model were established.It was found that the critical initial Jeffreys-Keulegan parameter increased with the diversion angle of the braided river model.

The results of the present study will help us to understand the characteristics of strati fied flow in braided rivers,and provide a signi ficant basis for further research on strati fied flow in rivers.

Chu,K.J.,Hua,Z.L.,Wang,H.M.,Xing,L.H.,2004.Experimental investigation on stability of strati fied shear flows in open channel with a bending angle of 45°.J.Hohai Univ.Nat.Sci.32(6),640-643.

Chu,K.J.,2006.Laboratory Investigation and Numerical Simulation of Thermally Strati fied Shear Flow(Ph.D.Dissertation).Hohai University,Nanjing(in Chinese).

Chu,K.J.,Hua,Z.L.,Xing,L.H.,Gu,L.,2008.Entrainment and shear instability of strati fied flow in curved flume with 90°bend.In:Proceedings of 16th IAHR-APD Congress and 3rd Symposium of IAHRISHS Advancesin WaterResourcesand HydraulicEngineering,pp.551-555.

Donda,J.M.M.,van Hooijdonk,I.G.S.,Moene,A.F.,Jonker,H.J.J.,van Heijst,G.J.F.,Clercx,H.J.H.,van de Wiel,B.J.H.,2015.Collapse of turbulence in stably strati fied channel flow:A transient phenomenon.Q.J.R.Meteorol Soc.141(691),2137-2147.https://doi.org/10.1002/qj.2511.

Drazin,P.G.,1958.The stability of a shear layer in an unbounded heterogeneous inviscid fluid.J.Fluid Mech.4(2),214-224.https://doi.org/10.1017/S0022112058000409.

Galperin,B.,Sukoriansky,S.,Anderson,P.S.,2007.On the critical Richardson number in stably strati fied turbulence.Atmos.Sci.Lett.8(3),65-69.https://doi.org/10.1002/asl.153.

García-Villalba,M.,DelA■lamo,J.C.,2011.Turbulence modi fication by stable strati fication in channel flow.Phys.Fluids 23(4),045104.https://doi.org/10.1063/1.3560359.

Gu,L.,Yuan,H.,Hua,Z.L.,Wang,L.L.,Li,Q.L.,Jiao,Z.N.,2014.Turbulence characteristics of strati fied flow in braided river with varied velocity ratios and width ratios.J.Hohai Univ.Nat.Sci.42(2),130-136.https://doi.org/10.3876/j.issn.1000-1980.2014.02.007.

Gu,L.,Li,Q.L.,Hua,Z.L.,Wang,L.L.,Yuan,H.,2015.Thermal-hydraulic characteristics of strati fied shear flow in braided rivers.J.Hydraulic Res.53(6),747-759.https://doi.org/10.1080/00221686.2015.1060269.

Harleman,D.R.F.,1961.Strati fied flow.In:Streeter,V.(Ed.),Handbook of Fluid Dynamics,Chapter 26.McGraw-Hill,New York.

Hua,Z.L.,Chu,K.J.,2008.Experiments and Numerical Simulations on Characteristics of Thermally Strati fied Flow.Science Press,Beijing(in Chinese).

Hua,Z.L.,Gu,L.,Chu,K.J.,2009.Experiments of three-dimensional flow structure in braided rivers.J.Hydrodyn Ser.B 21(2),228-237.https://doi.org/10.1016/S1001-6058(08)60140-7.

Huai,W.X.,Li,Z.W.,Qian,Z.D.,Zeng,Y.H.,Han,J.,Peng,W.Q.,2010.Numerical simulation of horizontal buoyant wall jet.J.Hydrodyn Ser.B 22(1),58-65.https://doi.org/10.1016/S1001-6058(09)60028-7.

Jeffreys,H.,1925.On the formation of water waves by wind.Proceedings R.Soc.A Math.Phys.Engineering Sci.107(742),189-206.https://doi.org/10.1098/rspa.1925.0015.

Jin,H.S.,Zhang,S.N.,1992.Stability and numerical simulation of turbulent strati fied flows.Hydro Sci Engineering 6(2),121-131(in Chinese).

Keulegan,G.H.,1949.Interfacial instability and mixing in strati fied flows.J.Res.Natl.Bureau Stand.11(43),487-500.

Li,Q.L.,2014.Turbulent Characteristics Near Interface of Thermally Stratifi ed Shear Flow in Braided River(M.E.Dissertation).Hohai University,Nanjing(in Chinese).

Miles,J.W.,1961.On the stability of heterogeneous shear flows.J.Fluid Mech.10(4),496-508.https://doi.org/10.1017/S0022112061000305.

Richardson,W.R.,Thorne,C.R.,1998.Secondary currents around braid bar in BrahmaputraRiver,Bangladesh.J.HydraulicEngineering 124(3),325-328.https://doi.org/10.1061/(ASCE)0733-9429(1998)124:3(325).

Richardson,W.R.,Thorne,C.R.,2001.Multiple thread flow and channel bifurcation in a braided river:Brahmaputra-Jamuna River,Bangladesh.Geomorphology 38(3-4), 185-196. https://doi.org/10.1016/S0169-555X(00)00080-5.

Rohr,J.,Van Atta,C.,1987.Mixing ef ficiency in stably strati fied growing turbulence.J.Geophys.Res.92(C5),5481-5488.https://doi.org/10.1029/JC092iC05p05481.

Schiller,E.J.,Sayre,W.W.,1975.Vertical temperature pro files in open-channel flow.J.Hydraul Div.101(6),749-761.

Schmid,B.H.,Hengl,M.A.,Stephan,U.,2004.Salinity-induced density strati fication in near-laminar open-channel flows.J.Hydraulic Engineering 130(12),1206-1210.

Sherekov,I.A.,Netjuhalio,A.P.,Teleshkin,E.D.,1971.Research investigation of transfer process in two-dimensional strati fied flow.In:Proceedings of the XIVth Congress of the International Association for Hydraulic Research(IAHR),pp.217-226.

Taylor,G.I.,1931.Effect of variation in density on the stability of superposed streams of fluid.Proceedings R.Soc.A Math.Phys.Engineering Sci.132(820),499-523.https://doi.org/10.1098/rspa.1931.0115.

Wang,L.L.,2015.Lateral Circulation Characteristics and Temperature Distribution of Thermally Strati fied Flow in Braided River(M.E.Dissertation).Hohai University,Nanjing(in Chinese).

Williamson,N.,Arm field,S.W.,Kirkpatrick,M.P.,Norris,S.E.,2015.Transition to stably strati fied states in open channel flow with radiative surface heating. J. Fluid Mech. 766, 528-555. https://doi.org/10.1017/jfm.2014.711.

Yu,X.M.,Tan,G.M.,Zhang,Y.,Zhao,P.,2007.Experiment on transportation characteristics of flow and sediment in distributaries channel.Engineering J.Wuhan Univ.40(4),9-12.https://doi.org/10.3969/j.issn.1671-8844.2007.04.003(in Chinese).

Zeng,Y.H.,Huai,W.X.,2005.Numerical study on the stability and mixing of vertical round buoyant jet in shallow water.Appl.Math.Mech.26(1),92-100.https://doi.org/10.1007/BF02438370.

This work was supported by the National Natural Science Foundation of China(Grants No.51379058,51379060,and 51479064),the Priority Academic Program Development of Jiangsu Higher Education Institutions(PAPD Project),and the Fundamental Research Funds for the Central Universities(Grants No.2016B06714 and 2014B07814).

*Corresponding author.

E-mail address:guliqc@hhu.edu.cn(Li Gu).

Peer review under responsibility of Hohai University.