对相控阵雷达副瓣的双极化干扰研究

韩 昭，胡 东

(南京电子技术研究所，江苏 南京 210039)

对相控阵雷达副瓣的双极化干扰研究

韩 昭，胡 东

(南京电子技术研究所，江苏 南京 210039)

相控阵雷达普遍采用自适应数字波束形成技术，能够有效对抗副瓣干扰。随着计算能力的提升，波束形成算法可以做到接近实时运算。这导致多点源闪烁干扰、重复噪声干扰等以往有效的方法效果也被大大削弱。自适应波束形成技术的原理是窄带条件下多个雷达天线单元接收到同一干扰机的信号高度相关。由于天线单元必然存在交叉极化分量，不同单元的交叉极化方向图有较大的幅相不一致性。基于这一点，利用一台干扰机产生2路极化不同的干扰信号，能够改变多个天线单元接收到数据的固有的相关性，从而消耗更多的雷达空域自由度。理论分析和仿真结果证明了上述结论。

雷达副瓣；自适应数字波束形成；双极化干扰；相控阵雷达

0 引 言

现代相控阵雷达普遍采用多通道数字阵，模数采样后联合多通道数据进行数字信号处理，达到干扰抑制的目的[1]。多通道联合的处理方法主要有自适应数字波束形成(ADBF)、自适应副瓣对消(ASLC)以及空时二维自适应处理(STAP)等技术。这3种技术在对抗副瓣有源干扰时，本质上是一样的，区别在于ADBF 是直接在波束形成时抑制干扰，ASLC在固定波束下依靠辅助天线，STAP在空域基础上联合时域，目的是为了对抗由于载机运动导致频谱展宽的高强度杂波。这些技术对副瓣干扰有很强的抑制效果，使得电子对抗面临着很大的挑战[2]。本文以ADBF为例，分析了其算法处理的本质是窄带条件下阵元间接收数据的高度相关性，指出时域及频域的调制都难以提高干扰效果。雷达的接收天线普遍存在交叉极化分量，而且交叉极化方向图存在不一致性。当采用双极化干扰时，如果2个极化分量单独可控，那么雷达抑制一个干扰源需要消耗更多的自由度。理论推导及仿真证明了该结论。

1 ADBF原理

为方便讨论，考虑一维等距线阵与方位角，雷达阵元接收到从某一方向入射的信号可表示为如下的向量形式：

(1)

式中：aJ为信号幅度；λ为雷达中心频率对应的波长；θ为方位入射角。

由于雷达的窄带处理特性，信号进入雷达接收机后要经过窄带滤波，滤波后的带宽远远小于雷达载频，从而信号可以近似表示成式(1)形式。

ADBF的处理可以用图1所示的框图表示，目的是保持目标信号增益的同时抑制有源干扰信号。假设此时雷达波束指向为θ0，M个干扰源所在方位为θ1～θM，那么约束方程可以表示为：

容易看出，ABDF的最优权值实际上就是线性方程组的解，天线阵元的数量N对应着系统的空域自由度，保持波束主瓣增益需要消耗1个自由度，1个干扰源需要1个自由度去对消，因此，为了使方程组有解，干扰源的数目不能大于N-1。在实际的处理过程中，事先并不知道干扰源所在角度，因此不能直接列出上面的方程组，而是使用大量数据样本基于统计意义下的最小方差无偏估计进行求解，求出的最优权值为：

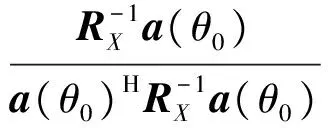
(3)

式中：a(θ0)为目标的导向矢量，也就是主波束指向。

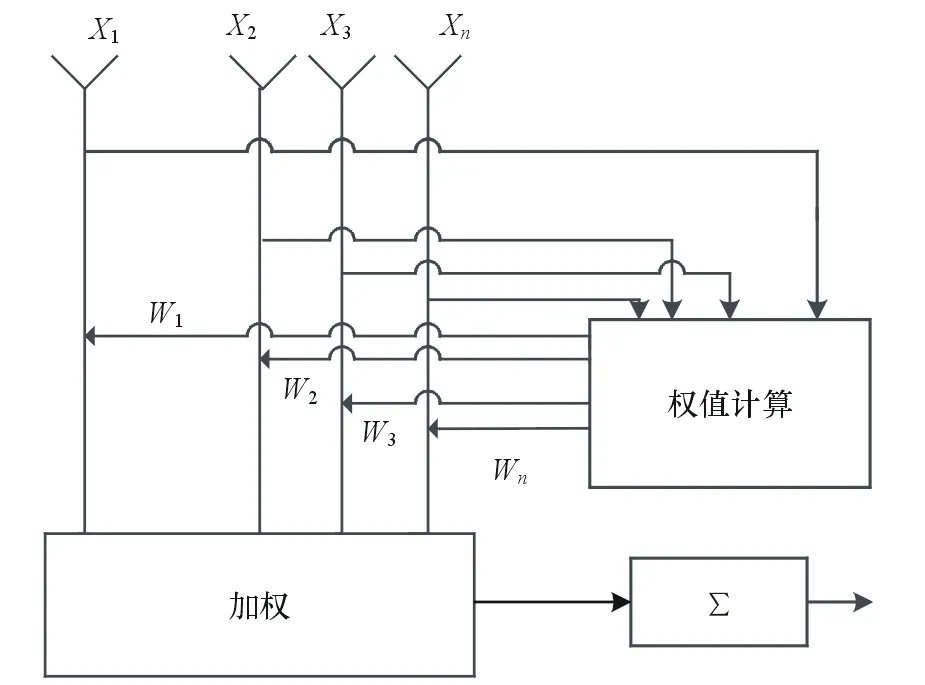
图1 ADBF实现框图

虽然表达形式有所改变，但本质依然是利用信号间的线性关系进行对消[3-5]。

2 天线对信号幅相的影响

针对ADBF对消干扰的原理，从外场录取了某相控阵雷达不同数字通道接收的干扰数据进行相关度分析，结果如图2所示。

图2上部是通道1的数据，下部是通道2的数据，左侧是一段时间内的信号幅度，右侧是时频图。可以看到，从一个固定方位到达的干扰信号在不同数字通道高度相关，可以求出两通道的幅度相关性超过99%。从时频图也可以看到，两通道接收到的信号是一致的。这种相关性与干扰波形没有关系，只要在处理过程中能够获取到足够的干扰信号样本，就可以完成对消，因此，ADBF对抗各种类型的副瓣干扰都能取得不错的效果。

对抗ADBF的思路大致可以分为2种：一是时域控制干扰信号，使得雷达难以选取合适的样本；二是利用一个干扰源尽量多地消耗雷达空域自由度，从而节约干扰成本。对于现代雷达的处理方式，第1种思路越来越难，因此本文考虑第2种思路。

一般情况下，雷达天线是水平极化或垂直极化，在有主极化分量的同时，还有交叉极化分量，也可以理解为任何实际的天线极化形式都是椭圆极化，只是一般情况下交叉极化分量比较小。对于相控阵雷达的天线单元来说，主极化的一致性一般是比较好的，但交叉极化却随着各种因素在不同天线间表现出较大差异。从前面的理论分析中知道，因为干扰在不同通道产生信号的线性关系，所以一个干扰源方位只能消耗雷达一个自由度。如果干扰引入交叉极化分量，并且交叉极化的幅相不一致性改变了这种关系[6-9]，那么就可能实现单个干扰源消耗雷达多个自由度的目的。

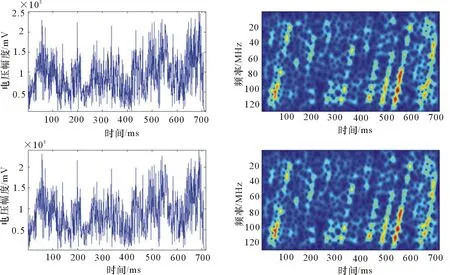
图2 数字通道间数据幅度图与时频图

雷达用来进行ADBF处理的每个阵元的包含幅相影响的增益可以表示成向量的形式，天线对主极化信号的幅相影响为：

A‖=G‖((1+δ1‖)ejφ1‖,(1+δ2‖)ejφ2‖,…,

(1+δN‖)ejφN‖)

(4)

天线对交叉极化信号的幅相影响为：

A⊥=G⊥((1+δ1⊥)ejφ1⊥,(1+δ2⊥)ejφ2⊥,…,

(1+δN⊥)ejφN⊥)

(5)

式中：符号‖表示水平极化分量；⊥表示垂直极化分量。

假设水平极化为主极化，如果仅考虑天线的主极化分量，这种幅相不一致会对最优权值的形成产生影响，使得期望方向的增益降低，但并不影响干扰信号的抑制；而如果同时考虑交叉极化分量，结果则有所不同。

3 双极化干扰理论分析

天线对信号的影响由式(4)、式(5)表示，分析过程按干扰信号的极化方式不同分情况考虑。

3.1 干扰为纯线极化

当干扰信号为纯线极化，与天线主极化方向夹角为θ，幅度为aJ，那么，经天线后在雷达通道产生的信号为：

J‖=aJG‖cosθ((1+δ1‖)ejφ1‖，

(6)

J⊥=aJG⊥sinθ((1+δ1⊥)ejφ1⊥,

(7)

此时，只有一个干扰源，如果要分别抑制这2个极化的干扰，权值的选择应满足:

(8)

方程组(8)中，第1个方程是为了保证目标增益，第2个方程是对消干扰的主极化分量，第3个方程对消干扰的交叉极化分量，显然第2个与第3个方程线性无关，但这并不能更多地消耗雷达自由度。因为抑制干扰并不需要分别使主极化和交叉极化为0，而是干扰信号总和为0，所以方程组(8)的后两式应合并改写为:

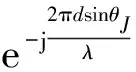
(9)

由于天线增益和幅相误差在比较小的空域、频域范围内一般为定值，可以看到，在式(9)中，虽然由于各种误差以及交叉极化的存在使表达式变得复杂，但是对于干扰方来说可调节的参数只有aJ，无论如何调整都不影响整个关系式。可以得到结论，即使考虑幅相误差与交叉极化，ADBF仍然只需要一个自由度抑制线极化干扰。

3.2 干扰为纯圆极化或纯椭圆极化

当干扰为纯圆极化或纯椭圆极化，可以得到与干扰是纯线极化相同的结论。这是因为圆极化或椭圆极化都可以看成是2路正交线极化的合成，并且这2路信号的幅相之间相关，即幅度之比为定值，且有固定相位差。当2路正交线极化幅度相等、相位相差90°时，为圆极化；当2路正交线极化幅度不相等或相位相差不为90°整数倍时，为椭圆极化。

不论极化方式如何改变，求解使得干扰信号对消的权值总能用一个方程表示，而且方程中可以调整的参数只有干扰信号幅度aJ；因此，如果只使用一路干扰，无法实现消耗雷达更多自由度的目的。

3.3 2路极化方式不同的干扰

为方便讨论，考虑干扰源从一个角度发出分别对应雷达主极化和交叉极化的干扰，并且2路干扰的幅度、相位都可以独立改变。假设干扰的幅度分别为aJ1和aJ2，那么抑制干扰的方程可以表示为：

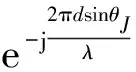
(10)

由于aJ1和aJ2都是可调整的，对于不同的快拍，改变aJ1和aJ2，就可以让阵元间接收到的数据关系发生变化，从而使得一个自由度无法完整地表示阵元间干扰数据的关系。但是这种情况也不是无法完成对消，显然可以看到，如果把它们看成2个独立的互不相关的干扰，那么如(8)所示的方程组后两式可以对它们分别进行抑制，只是在这种情况下，从一个物理位置发出的干扰就需要2个雷达空域自由度才能实现对消。

如果2路干扰的极化方式是任意的，由于总可以将其分解成对应雷达主极化和交叉极化，所以并不影响上述结论。

4 仿真验证

使用Matlab仿真了在这种情况下干扰所产生的效果。仿真模型取一维线阵，阵元数为10个，只考虑方位角，目标位于方位50°，5台干扰设备分别位于30°、40°、60°、70°、80°。每台干扰设备都包含独立可控的主极化与交叉极化干扰，主极化方式与雷达一致。仿真过程中同时考虑雷达阵元的主极化与交叉极化幅相误差，雷达天线主极化增益比交叉极化增益平均大25 dB，结果如图3和图4所示。

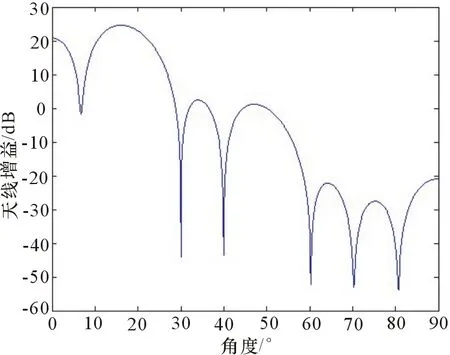
图3 无交叉极化干扰情况

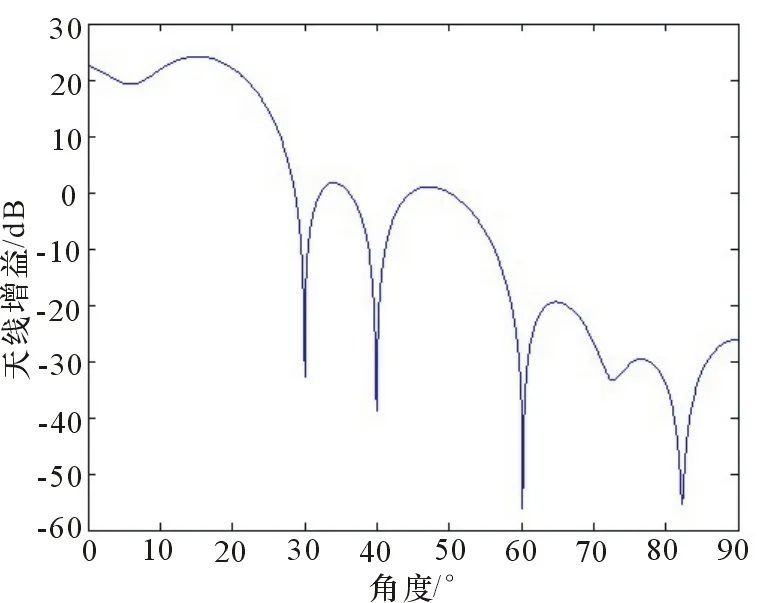
图4 有交叉极化干扰情况

图3和图4是补偿了幅相一致性后的主极化方向图，因此，横坐标角度与实际角度是对应的。从图3可以看到，不考虑交叉极化时，由于干扰源数量小于空域自由度，在5个干扰方向都形成了零陷。图4显示了在考虑交叉极化的情况下，虽然交叉极化的天线增益小于主极化，但仍然要消耗雷达的空域自由度。由于对消干扰的同时要保证期望方向增益，自由度不足，没有形成70°、80°的零陷。

如果把雷达阵元数减少为8个，仿真结果如图5和图6所示。

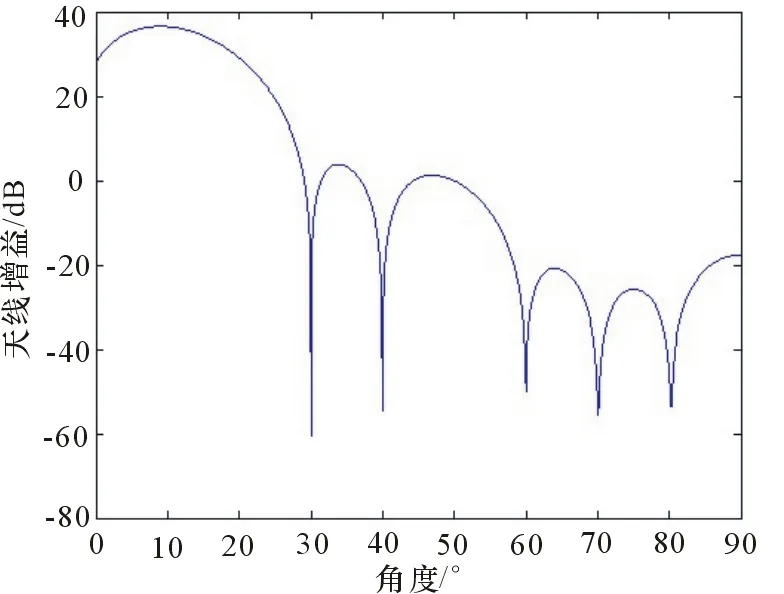
图5 无交叉极化干扰情况

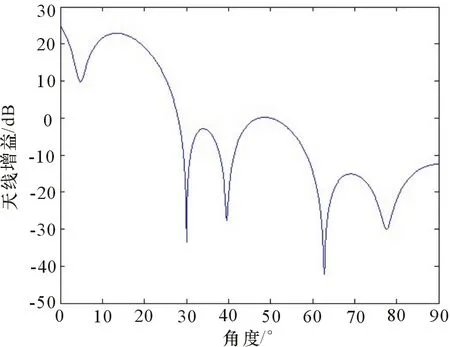
图6 有交叉极化干扰情况

可以看到，没有交叉极化干扰时，仍有充足的自由度对消主极化干扰；而对于有交叉极化的情况，进一步减少自由度会使得对消效果继续降低。对于仿真的情况，60°、70°、80°都没有形成零陷，30°、40°的干扰抑制效果也有所下降。仿真图中，50°为期望方向，为了计算方便，仿真过程没有考虑单阵元方向图与为降低副瓣的加权，所以出现了非期望方向增益大于期望方向，并不影响讨论问题的核心。

5 结束语

从上面的分析可知，由于天线交叉极化的存在，交叉极化方向图的不一致性使得干扰方可以实现一个干扰源消耗雷达2个空域自由度。这是由于虽然干扰从一个物理方向发出，但交叉极化和主极化信号在不同通道间反映出不同的线性关系。如果交叉极化干扰和主极化干扰是相关的，那么合成后的干扰会表现出稳定的极化方式，仍然可以用一个线性方程代表抑制干扰的表达式；而如果它们相互独立，则可以看成2个干扰，从而消耗雷达2个自由度。

由于一般情况下天线的交叉极化增益比主极化增益低，所以交叉极化的干扰强度比较弱。但对于雷达来说，稍微抬高底噪可能就会大幅降低其发现概率或增大虚警率。在体系化作战的今天，使用大量低成本的无人设备组网协同工作是一种趋势，可以在减少一半设备平台的基础上对雷达实施干扰，便能够得到作战效能的大幅提升，因此，该方法具有重要意义。

[1] 李仙茂,罗景青.多方位干扰对抗雷达旁瓣对消的效果分析[J].航天电子对抗，2003(6)：25-28.

[2] 齐立峰，冯新喜，侯宏伟.雷达旁瓣对消系统攻防对抗技术研究[J].现代雷达，2003，25(4):12-15．

[3] 李森，李彦志，张国毅，等.对自适应旁瓣对消系统的闪烁干扰方案研究[J].现代雷达，2012，34(2)：51-54.

[4] 宁勇.对相控阵雷达旁瓣干扰方法研究[J]．电子对抗，2009(6)：1-7.

[5] 侯民胜，朱莹，樊晓明.单脉冲雷达的闪烁干扰技术研究[J]．现代电子技术，2009(15)：1-3.

[6] 王永良，吴仁彪.通遭不一致性、互耦对最优阵列处理器的影响[J].系统工程与电子技术，1993，15(2):49-55.

[7] WORMS G J.About the influence of polarization agile jammers to adaptive antenna array[C]//IEEE Proceeding of Radar 95,USA,1995:619-623.

[8] 倪晋麟，苏为民，储晓彬.幅相不一致性对自适应阵列性能的影响[J].应用科学学报，2000，18(3):41-44.

[9] 倪晋麟，郑学誉，何东元.单元交叉极化对自适应阵列性能的影响[J].电子与信息学报，2002，24(1):97-101.

StudyofDual-polarizationJammingtoPhasedArrayRadarSide-lobe

HAN Zhao,HU Dong

(Nanjing Research Institute of Electronic Technology,Nanjing 210039,China)

Phased array radars generally use adaptive digital beam-forming (ADBF) technology,which can effectively antagonize side-lobe interference.Along with the advancement of calculation capability,beam-forming algorithm can be close to the real time operation,which leads to the effect of effective methods in the past such as multi-source blinking jamming,repeat noise jamming,etc.have been greatly weakened.The principle of ADBF technology：under the condition of narrow band,the signals from the same jammer

by multiple radar antenna units are highly correlated.The cross-polarization component is inevitable in the antenna unit,and there are large differences of amplitude/phase in the cross-polarization antenna pattern of different units.Based on this,this paper uses one jammer to produce two jamming signals with different polarization mode,which can change the inherent correlation of the received data from the antenna units,thereby more spatial freedom degrees of radar are consumed.Theoretical analysis and simulation results prove the above conclusion.

radar side-lobe；adaptive digital beam-forming;dual-polarization jamming;phased array radar

TN972.1

A

CN32-1413(2017)05-0001-05

10.16426/j.cnki.jcdzdk.2017.05.001

2017-05-15