一类多面集投影算子方向导数的研究

刘勇进，李若男

(沈阳航空航天大学 理学院，110136)

基础科学与工程

一类多面集投影算子方向导数的研究

刘勇进，李若男

(沈阳航空航天大学 理学院，110136)

首先刻画了一类多面集的对偶锥和极锥，进而给出了这类多面集上投影算子方向导数的具体计算方法，研究结果不仅为该类多面集投影算子广义次微分的刻画提供了技术支持，也为相关优化问题的灵敏度分析和算法收敛性分析奠定了理论基础。

投影算子；多面集；方向导数；对偶锥；极锥

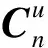
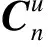
(1)

其中0≠ui∈-,+。上述定义的多面集与加权l1、l范数上图锥有着密切的联系，其中加权l1范数上图锥记为定义为

加权l范数上图锥记为定义为

其中W=diag(w1,w2,…,wn)是对角矩阵，且其对角线元素wi>0，i=1,2,…,n，‖·‖1表示的是l1范数，‖·‖表示的是l范数，也即，对任意的由此看出加权l1、l范数上图锥就是这类多面集的特殊形式。

2011年，修乃华[6]等对加权l范数上图锥投影算子进行了研究，并给出其具体表达式。刘梅娇等[7]于2013年利用闭凸锥上投影算子应满足的条件，分情况讨论给出了l1范数上图锥的计算公式。刘勇进等[8]在2013年的文章里提出了计算在半封闭空间和盒子变量上的向量投影的快速算法，最终可以用来计算Ky-Fank范数上图锥的投影算子。2014年，丁超等[9]在他们的文章中给出了l1、l范数上图锥投影算子的计算方法，并且讨论了其方向导数的具体表达形式。2015年，刘勇进等[10]详细研究了加权l1/l上图锥投影算子的微分性质，主要包括投影算子的方向导数、B次微分和Clarke广义Jacobian矩阵等。2016年，刘勇进等[11]又给出了一类特殊闭凸锥，即非负卦限上投影的l1范数上图锥，较为丰富的理论结果，着重研究了它的变分和微分性质，详细地描述了其对偶锥、切锥、法锥和临界锥的表达形式，并刻画了它的方向导数、B次微分和Clarke广义Jacobian矩阵等。

记号说明：如果I是一个集合，则|I|表示集合I的基数。若C是闭凸集，则intC表示C的内部，bdC表示C的边界。为方便起见，在有限维实Hilbert空间上，内积均记为〈·,·〉，它诱导的范数记为‖·‖。

设H是有限维实Hilbert空间，令C是H上的闭凸集，则C的对偶锥定义为

C*:=y∈H:〈x,y〉≥0,∀x∈C，

且有C的极锥C°:=-C*。

记ΠC(·)为闭凸锥C上的投影算子，即对任意给定的x∈H，ΠC(x)是如下凸优化问题的唯一最优解：

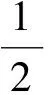
s.t.y∈C。

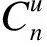
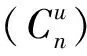
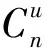
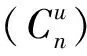
(2)

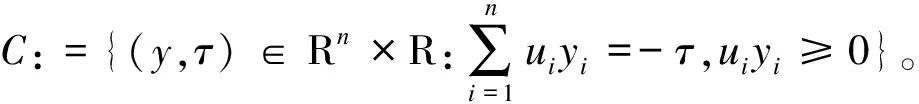
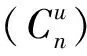
(3)

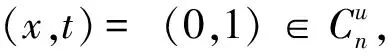
(4)

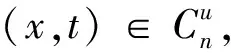
(5)

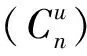
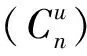
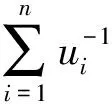
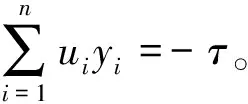
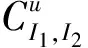
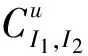
引理1 假设给定(x,t)∈Rn×R和u∈Rn。令π是{1,2,…,I2}的一个排序使得

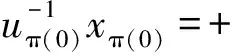
定义

且对于i=1,2,…,n有

推论1假设给定(x,t)∈Rn×R和u∈Rn，我们有以下结论：

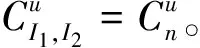
其中

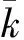
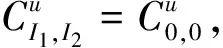
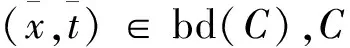
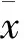
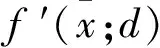
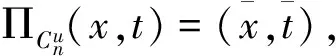
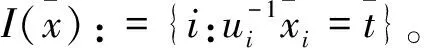
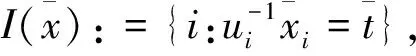
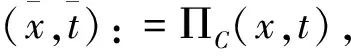
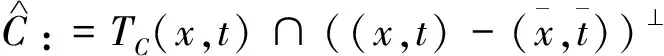
根据推论1，对给定的(x,t)∈Rn×R和u∈Rn，定义指标集α,β和γ为

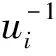
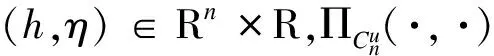
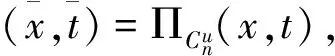
(6)

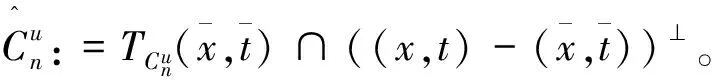
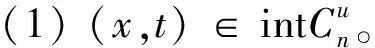
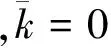
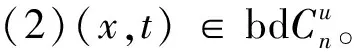
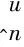
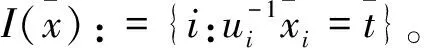
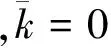
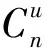
由此可得

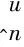
则由(6)可得

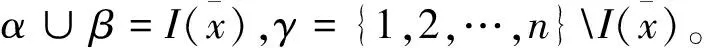
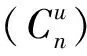
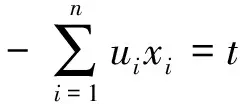
则有

由此推得

由(6)可以推知

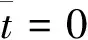
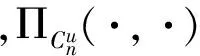
3 结论

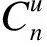
[1] BONNANS J F,SHAPIRO A.Perturbation analysis of optimization problems [M].Springer,New York,2000.

[2] 张立卫,吴佳,张艺.变分分析与优化 [M].北京:科学出版社,2013.

[3] BONNANS J F,RAMIREZ C H.Perturbation analysis of second-order cone programming problems[J].Mathematical Programming,2005,104(2):205-227.

[4] WANG Y,ZHANG L W.Properties of equation reformulation of the Karush-Kuhn-Tucker condition for nonlinear second order cone optimization problems[J].Mathematical Methods of Operations Research 2009,70(2):195-218.

[5] SUN D F.The strong second order sufficient condition and constraint nondegeneracy in nonlinear semidefinite programming and their implications[J].Mathematics of Operations Research,2006,31(4):761-766.

[6] 王英楠,修乃华.几类非对称矩阵锥分析 [D].北京:北京交通大学,2011.

[7] 刘梅娇,单锋,姜永.范数锥投影算子的计算[J].数学进展,2013,42(4):563-568.

[8] LIU Y J,WANG S Y,SUN J H.Finding the projection onto the projection onto the intersection of a closed half-space and a variable box[J].Operations Research Letters,2013,41(3):259-264.

[9] DING C,SUN D F,TOH K C.An introduction to a class of matrix cone programming[J].Mathematical Programming,2014,144(1-2):141-179.

[10]LIU Y J,HAN N,WANG S Y,etal.Differential properties of the metric projectors over the epigraph of the weighted and norm[J].Pacific Journal of Optimization,2015,11(4):737-749.

[11]LIU Y J,WANG L.Properties associated with the epigraph of the l1 norm function of projection onto the nonnegative orthant[J].Mathematical Methods of Operations Research,2016,84(1):205-211.

[12]韩宁,刘勇进,刘梅娇.一类闭凸锥上投影算子的计算[J].沈阳航空航天大学学报,2013,30(5):88-91.

[13]CLARKE,F H.Optimization and nonsmooth analysis [M].New York:John Wiley & Sons,1983.

[14]HARAUX P T.How to differentiate the projection on a convex set in Hilbert space[J].Journal of the Mathematical Society of Japan,1977,29:615-631.

[15]PANG J S.Newton′s method for B-differentiable equation[J].Mathematics of Operations Research,1990,15(1-3):149-160.

Researchonthedirectionalderivativeoftheprojectoroveraclassofpolyhedralsets

LIU Yong-jin，LI Ruo-nan

(College of Science,Shenyang Aerospace University,Shenyang 110136,China)

This paper characterizes the specific structure of the dual cone and the polar cone of a class of polyhedral sets and then presents the explicit formula of the directional derivative of the projector over this kind of polyhedral sets.The results achieved in this paper provide technical support for the characterizations of the generalized differential of the polyhedral sets,as well as lay theoretical foundations for the sensitivity analysis and the convergence analysis of methods for the related optimization problems.

projector;polyhedral sets;directional derivative;dual cone;polar cone

2017-09-08

国家自然科学基金面上项目(项目编号：11371255);辽宁省“百千万人才工程”项目(项目编号：辽百千万立项[2015]51号)

刘勇进(1977-)，男，江西赣州人，教授，主要研究方向：优化理论与方法、矩阵优化、数值计算，E-mail：yjliu@sau.edu.cn。

2095-1248(2017)05-0081-05

0221.2

A

10.3969/j.issn.2095-1248.2017.05.012

(责任编辑：刘划 英文审校：靖可)