以椭圆为例研究圆锥曲线的由来及其解析定义

江西省宜春中学2018届高三（22）班 宋 禹

以椭圆为例研究圆锥曲线的由来及其解析定义

江西省宜春中学2018届高三（22）班 宋 禹

高中数学教材将椭圆、双曲线、抛物线归在圆锥曲线章节中，这在当时给我及许多初学的同学带来了一些疑惑。不管是第一定义、第二定义还是性质与判断，这三种曲线似乎都与圆锥并无联系，为什么它们会被命名为圆锥曲线呢？

为了解开这个疑惑，笔者查阅资料研究圆锥曲线的发展历史。原来，最初这几种曲线就是用平面切割圆锥得到的，故命名为圆锥曲线。在2000多年前，古希腊数学家阿波罗尼斯在他的著作《圆锥曲线》中，记载了用不同角度的平面去截一个二次锥面，得到的交线中就包括椭圆、双曲线、抛物线及一些退化情形（圆和直线）。而我们现在所熟知的圆锥曲线的定义和性质，是在16世纪以后才由数学家们陆续发现的，之后对于圆锥曲线的研究更多偏向于解析几何方向，包括直角坐标系和极坐标系中。

然而，为什么用一个平面截圆锥就能得到椭圆等曲线？这些曲线为什么能满足解析几何下的定义？这仍然是困扰许多高中学生的问题。本文以椭圆为例，从平面几何和立体几何的角度证明，用平面截圆锥所得曲线确实可以满足椭圆的解析定义。因直接研究平面截圆锥较烦琐，本文先从证明平面截圆柱所得“圆柱曲线”为椭圆开始说明。

一、平面截圆柱

首先证明用一个平面截圆柱的侧面所得曲线为椭圆，具体可以简化为如下模型。

例1 如图1，平面α截圆柱得到曲线C，求证：曲线C为椭圆。

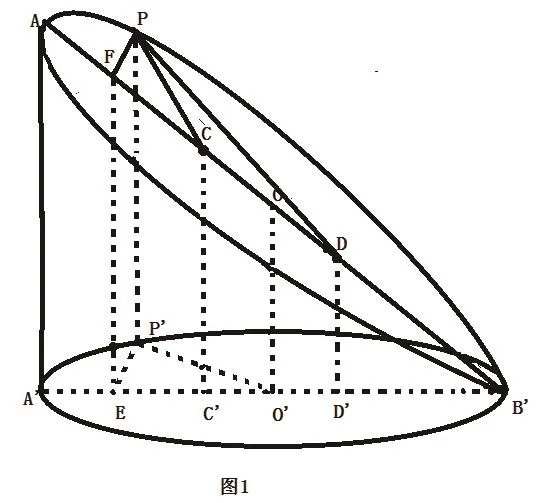
图1

分析：令A'B'＝ 2r，AA'＝ 2h，AB'＝2a，则有r2+h2=a2,证明椭圆可以通过其定义“到两定点的距离之和等于常数”来证明，但关键之处就是要确定椭圆的焦点位置，这里可以应用先猜后证的思想。图中可猜想其“长轴”为2a，“短轴”为2r，则得出其焦距为2h，如果在AB上取两点C、D，使CO＝DO＝h，那C、D可能就是两焦点，这之后如果能证明曲线上任意一点P，使得PC+PD=2a,问题就解决了。

证明：在线段AB上取C、D两点，使CO＝DO＝h，做出如图所示的辅助线，其中PF⊥AB'，P'E⊥A'B'，易得四边形PP′EF是矩形。

设P'E＝y，EO'＝x,则x2+y2=r2，

PC2=PF2+FC2=P'E2+（FE-CC'）2+（EO'-C'O'）2，

所以曲线C是以2a为长轴，2r为短轴，2h为焦距的椭圆。

这只是证明的第一步，只证明了所谓的“圆柱曲线”为椭圆。如果能证明平面截圆锥侧面所得曲线在底面的投影是一个圆，那么运用这个模型就可以直接得出该曲线可以是椭圆的结论，但投影是不是圆有待证明。

二、先猜后证

例2 如图2，平面α截圆锥形成曲线C，曲线C在圆锥底面的投影是不是圆？

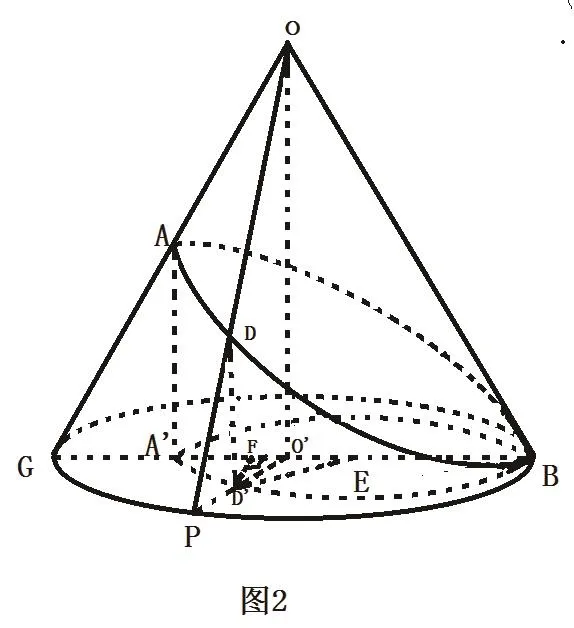
图2

思路：同样是先猜后证的思想，猜想它是个圆，之后找等量关系，即其上任意一点到圆心的距离相等。若能证明其是圆，问题便迎刃而解，若不是圆，用字母表示很难证出，最快的方法就是用特殊值法判断其有没有可能是圆。

解：用特殊值法判断。设底面圆半径R=1，圆锥的高H=3，AA'=2h=2，则h=1,取底面圆上任意一点P，连接PO',PO,PO交曲线C于D，PO'交曲线BA'于D'，曲线C的投影是曲线BA'，所以DD′与底面垂直。

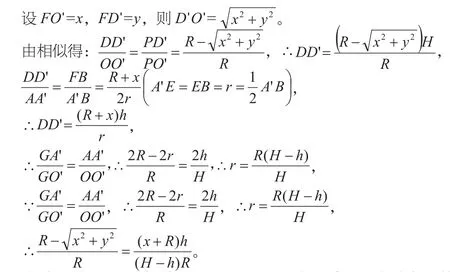
这样就得到了x,y的关系式，现在只需要将任意一个符合条件的x的值带入，求出ED'的值，将其与EA'比较，就可初步判断其是否可能为圆。

∴D'E≠A'E,所以曲线C在圆锥底面的投影不是圆。

这样便不能运用之前的那个模型，通过此方法也就无法说明曲线C为椭圆，所以这部分只当作先猜后证以及特殊值法的一种运用，激发读者想到更好的方法。

三、平面截椭圆柱

既然二中的投影不是圆，笔者就自然而然地想到了是椭圆，还是通过一中的方法，首先证明平面截椭圆柱得到的图形是椭圆。

例3 如图3，平面α截椭圆柱得到曲线C，求证：曲线C为椭圆。

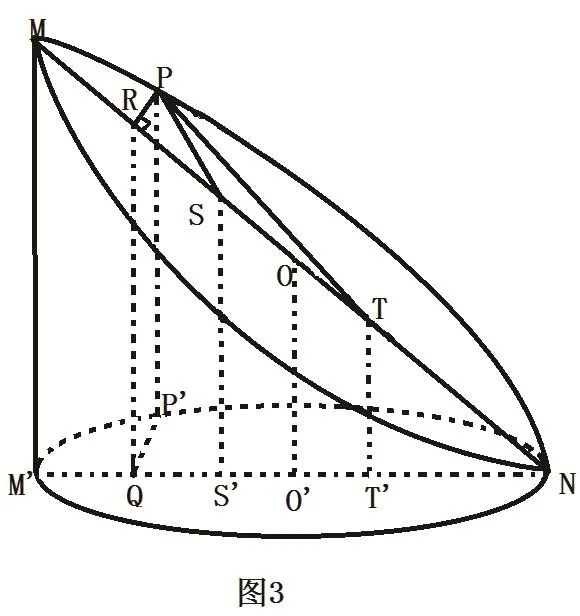
图3

分析：类似于一中先猜后证的思想方法，先找出其“焦点”位置令NM'=2a，MM'=2h，MN=2A，则有

设底面椭圆的半短轴长（即是曲线C的“半短轴”长）为b，曲线C的半焦距为C，则有同样的道理，只要在曲线C上找一点P，使得两“焦点”S、T的距离之和PS+PT=2A,即可得证。

解：设NM'=2a，MM'=2h，MN=2A，底面椭圆的半短轴长为b，则有在M、N上取两点S、T，使得SO=OT=C（其中

令m=PS+PT,化简可得：m=2A，所以曲线C为椭圆。

接下来，如果能证明圆锥曲线（椭圆）在底面圆的投影是椭圆，那么运用这个模型就可以解决这个问题了，这里就不再进行深入讨论读者有意可继续探究。

四、探究过程中发现的结论

回顾“一”中的探究过程，笔者发现了这样一个现象：

所证椭圆AB的离心率

在三角形BAA'中，sin∠ABA'=仔细观察发现，该角是平面与圆柱底面所成的二面角，所以可概括为：sinθ=e。（θ为平面截圆柱时，平面与圆柱底面所成二面角的大小，e为所截的椭圆的离心率）

本文是笔者为解开自己和同学们关于圆锥曲线的疑惑所做的研究，证明了椭圆的几何定义与解析定义的等价性，也发现了一些有益的结论，其中反复运用了先猜后证的思想。猜证思想是数学中重要的工具之一，许多伟大的数学定理都是科学家们先有大致的猜测再经过严格的证明得到。同样，在高中数学解题中，这也是一种很重要的思想，但是在实际操作过程中，同学们往往猜测之后没有严格证明，或者在证明过程中碰到困难就轻易放弃猜想，如在本文二中发现平面截圆锥所得曲线的投影不是圆后，就认为该曲线不是椭圆。这些问题都是同学们常犯的问题，希望本文能为大家对于猜证思想的运用带来更深的认识，大胆假设，细心求证！