高速公路交通流元胞自动机建模及大货车的影响分析
杨柳,龙科军,黄中祥
高速公路交通流元胞自动机建模及大货车的影响分析
杨柳,龙科军,黄中祥
(长沙理工大学公路工程教育部重点实验室,湖南长沙,410114)
在分析国内4车道高速公路交通特性的基础上,根据动机将换道分为无倾向型和有倾向型,描述法定换道规则,建立相应的元胞自动机模型,用实测交通流参数标定和验证模型。研究结果表明:随着大货车比率增大,大货车对快车道的占用增多,小客车速度降低,上述变化在大货车比率小于0.25时更显著并与密度相关;当大货车比率很小时,随着大货车动力性能降低,小客车速度降低,换道和冲突增多,这些变化在中密度区最显著;在临界密度附近,随着大货车比率变化,可随机观察到典型的移动瓶颈和偏析效应。
高速公路;双车道交通流;大货车;换道规则;元胞自动机;模拟
通过建立交通流模型,可实现对交通流现象的再现、解释和预测。王殿海等[1]根据建模思想将微观模型分为交通工程类和统计物理类,前者侧重于精确拟合实际驾驶参数来准确描述微观驾驶行为,后者侧重于用简单的微观驾驶规则来展现复杂的交通流宏观特性。不同模型对交通流现象的解释存在差异。贾宁 等[2]认为,模型是对现实的抽象描述,可能会存在局限,但只要能反映被模拟对象的关键特性就是有效的。元胞自动机模型属于统计物理类,因其具有离散、简洁、灵活、高效等特点而被广泛运用。以WOLFRAM[3]提出的184号规则为基础,NAGEL等[4]提出了单车道元胞自动机模型,简称NaSch或NS模型,能再现自发堵塞和时走时停波等现象。随后,各种改进模型不断被提出,以模拟更加复杂的交通现象。CHOWDHURY等[5]对单车道模型进行了分类总结。RICKERT等[6]以NaSch模型为基础提出了在双车道均质交通条件下的对称和不对称换道规则。CHOWDHURY等[7]将RICKERT换道规则扩展到快慢车混合交通条件下。NAGEL等[8]对双车道模型换道规则进行了归纳。杨柳等[9]将四车道高速公路在快慢车混行条件下的换道规则分为4种,建立了对应的元胞自动机模型,分析了各种换道规则造成的交通流运行差异。史峰等[10]建立了双车道环岛模型。敬明等[11−12]建立了考虑前车运动影响的双车道模型,探讨了更新步长和元胞尺寸对模拟结果的影响。国内高速公路以双向4车道居多,大货车占比高、尺寸大且性能差,严重影响小客车运行,容易引发移动瓶颈、造成拥堵甚至事故,使道路实际通行能力远低于设计通行能力,因此,探寻大货车对高速公路交通运行的影响规律,对改善交通现状具有重要意义。钟连德等[13]研究了高速公路交通流参数与事故率之间的关系,认为大车比率、大小车速度差和饱和度是影响交通安全的主要参数。梁国华等[14]在分析高速公路移动瓶颈的基础上,研究了大车比率对交通流稳定性的影响。刘有军等[15]考察了密度和慢车比率对高速公路流量、速度和换道的影响。肖瑞杰等[16−17]针对单车道和双车道情形,考察了车辆长度和速度对客货混合交通流的影响。付强等[18]分析了低速货车对不同类型驾驶人跟车行为的影响,建立了一种基于车头间距的跟车模型。冯树民等[19]建立了一种能表达高速公路货车结件行对的双车道元胞自动机模型,分析了货车结伴特性及对交通流的影响。上述研究还存在以下问题:1) 建模时没有充分考虑国内高速公路的车辆特性和换道规则;2) 对模型的参数标定和验证缺失或不充分;3) 没有全面分析大货车对交通流的影响。针对上述问题,本文作者首先分析我国高速公路的交通特性,然后提出相适应的元胞自动机模型,再用实测交通流参数标定和验证模型,最后通过模拟实验探讨大货车比率和动力性能对高速公路交通流的宏观影响规律。
1 国内高速公路交通特性与建模
1.1 高速公路交通特性
小客车和大货车是国内高速公路上的主要车型。小客车长度小、速度高、加减速性能好,大货车则相反。在高速公路平直路段的自由流状态下,小客车和大货车的期望速度分别为120 km/h和75 km/h[20]。
车辆只有遵守法定交通规则行驶,才能减少相互干扰,保证车流安全有序运行。我国现行的高速公路交通规则遵循2004年颁布并实行的“道路交通安全法实施条例”规定,当同向有2条车道时,左车道为快车道(或小客车道),右车道为慢车道(或客货车道)。小客车对2条车道都有使用权,大货车应使用慢车道,但可借用快车道超车,完成超越后应驶回慢车道。
1.2 纵向行驶规则建模
NaSch模型[4]高度简洁地描述了车辆运动中的加速、减速、安全性、随机性等本质问题,经过了长期实践检验,证明了其有效性。本文对其进行如下改进:1) 将加速步和确定性减速步合并为调整速度步; 2) 考虑车辆最大加速度;3) 考虑慢化减速度的随机性。在时间→+1过程中,按照如下规则演化。
1) 调整速度:→min(expect,),expect= min(+max,max);
2) 随机慢化:以概率令→max(-,0),rand(0,1)<,=randInt(1,max);
3) 更新位置:→+。
式中:expect为车辆期望速度;为车辆与前车的间距;max为车辆最大加速度,车辆按照优先使用最大加速度的原则行驶;max为车辆最大速度;为车辆慢化概率;rand(0,1)表示在区间[0,1]随机取值;为随机慢化时的减速度;max为车辆最大慢化减速度;randInt(1,max)表示在区间[1,max]随机取整数值,一般取max=max。
1.3 换道规则建模
法定交通规则表明不同类型的车辆在不同车道上的换道动机存在区别。为了描述这种区别,本文将换道分为无倾向型和有倾向型。
1) 无倾向型换道。车辆优先保持在当前车道行驶,换道只是为了改善行车条件。换道的动机条件是:只有在当前车道不能按期望速度行驶且邻道前方的行驶条件比当前车道好的情况下,才会产生换道动机。
2) 有倾向型换道。车辆优先换至邻道行驶,对邻道具有明显的倾向。换道的动机条件是:只要在邻道能按期望速度行驶或邻道前方的行驶条件不比当前车道差的情况下,就会产生换道动机。
综合以上分析,换道的充分条件可表述如下。
1) 动机条件:无倾向型换道应满足<min(other,expect),有倾向型换道应满足other≥min(,expect,expect= min(+max,max);
2) 安全条件:back other≥safe。
3) 随机条件:以概率c换道,即rand(0,1)<c。
式中:other为车辆与邻道前车的间距;back other为车辆与邻道后车的间距;safe为安全间距,保证车辆换道后与邻道后车不发生碰撞,取邻道后车的最大速度;c为车辆换道概率。
将换道分为有倾向型和无倾向型后,便能清晰描述我国四车道高速公路的换道规则,见表1。

表1 四车道高速公路换道规则
2 模型参数标定与验证
模型必须用真实交通流参数进行参数标定和验证后才能用于交通流模拟,模拟实验用VC++编程实现。
2.1 现场交通调查
交通调查的目的是获取通过调查断面的所有车辆的行驶车道、轴距、速度和车头时距等参数,计算密度和大货车比率,分车道分车型统计流量、速度、车道使用率、车头间距等交通流参数,作为验证模型的依据。调查对象为G4高速公路长沙段,调查路段限速120 km/h,调查方向为由北向南,调查日期为2014-01-15,天气为阴但能见度较好。通过现场踏勘,调查位置选定路线平直、路面状况良好、离匝道出入口较远的基本路段。
交通流数据采集用AxleLight RLU11路侧激光交通调查仪进行。该调查仪能根据轴距、轴数和轴组数将车辆分为13种类型。现场调查数据显示小客车和大货车占绝大多数,通过聚类分析,将轴距小于或等于3.8 m的车辆归为小客车,其他车辆归为大货车。
2.2 模型参数取值
模型参数可分为3类:模拟控制参数、交通参数和随机参数。综合文献[4−20]和实测交通流参数,对模型参数取值。
1) 模拟控制参数:元胞长度取3.5 m,采用周期边界和初始均匀分布,时间步长为1 s,每个样本运行10 000 s,统计5 000~10 000 s的运行数据,取50个样本进行统计平均。
2) 交通参数:道路长度取7 000 m,小客车长度7 m,最大速度126 km/h,最大加速度14 m/s,大货车长度14 m,最大速度75.6 km/h,最大加速度7 m/s。
3) 随机参数:慢化概率=0.2,换道概率c=0.8。
2.3 实测结果与模拟结果对比
根据实测参数,模拟实验条件设置为:密度=5.8辆/km,大货车比率=0.34,综合考虑天气和实际速度分布,小客车最大速度取113.4 km/h。大货车实测结果和模拟结果见表2,通过对比发现:模拟结果在流量、速度和车辆分布方面的各项统计参数都非常接近实测结果,能反映高速公路交通流的现实特性,证明参数取值合理、模型有效。

表2 实测结果和模拟结果对比
3 大货车影响的元胞模拟分析
为了全面探讨大货车比率和动力性能对交通流的影响,运用本文提出的元胞自动机模型进行模拟实验。为便于分析实验结果,定义以下统计特征量。
1)换道率,定义为车辆平均换道次数与统计时长的比值。合理换道可以改善交通状况,提高行车速度,但频繁换道会扰乱交通运行,增加行车风险。
2)车道使用率,定义为车辆使用某车道的平均时间与统计时长的比值,能描述车辆在各车道的分布情况,可反映客货车的分道行驶情况和相互干扰程度。
3)冲突率,定义为车辆平均急刹车次数与统计时长的比值。当减速度大于最大加速度时视为急刹车,冲突率可反映前后车之间的干扰程度。
交通最大流态所对应的密度称为临界密度,低于临界密度的区间分为低密度区和中密度区,合称中化密度区,高于临界密度的区间分为高密度区和致密区。模拟实验密度区间取0~60辆/km,不考虑致密区。实验结果被绘制成流量、速度、换道率、车道使用率、冲突率等参数与密度的关系曲线及时空斑图。
3.1 大货车比率的影响分析
为考察大货车比率的影响,分别取0,0.05,0.25,0.50和0.75,其余参数取值见2.2节,实验结果及分析如下。
不同大货车比率下的流量与密度关系见图1。从图1可见:最大流量随着的增大而减小,当≥0.25时,值对中低密度区的流量影响较小。
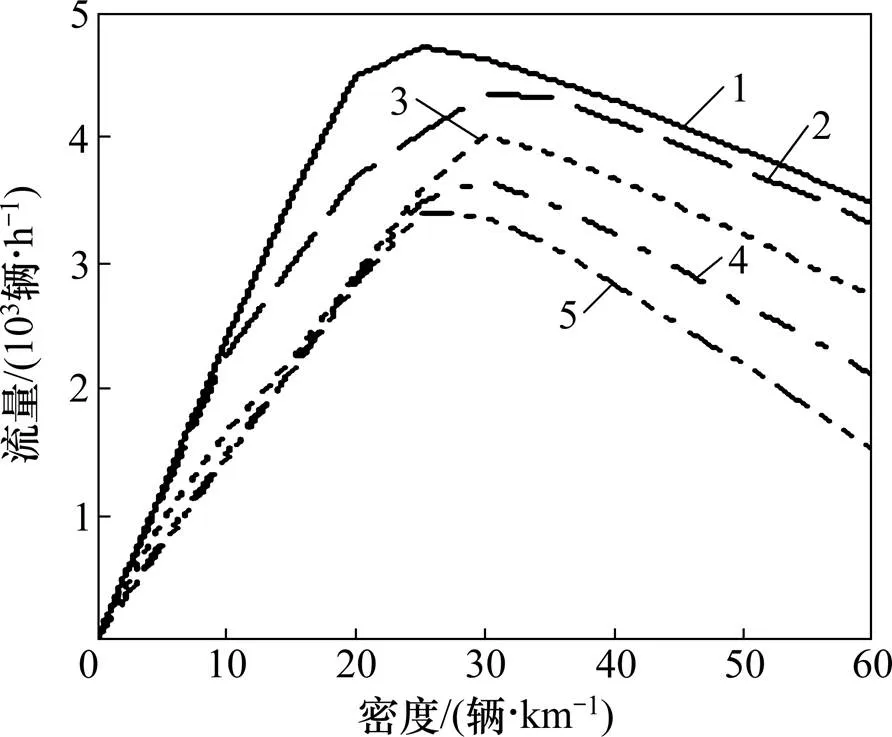
R:1—0;2—0.05;3—0.25;4—0.50;5—0.75。
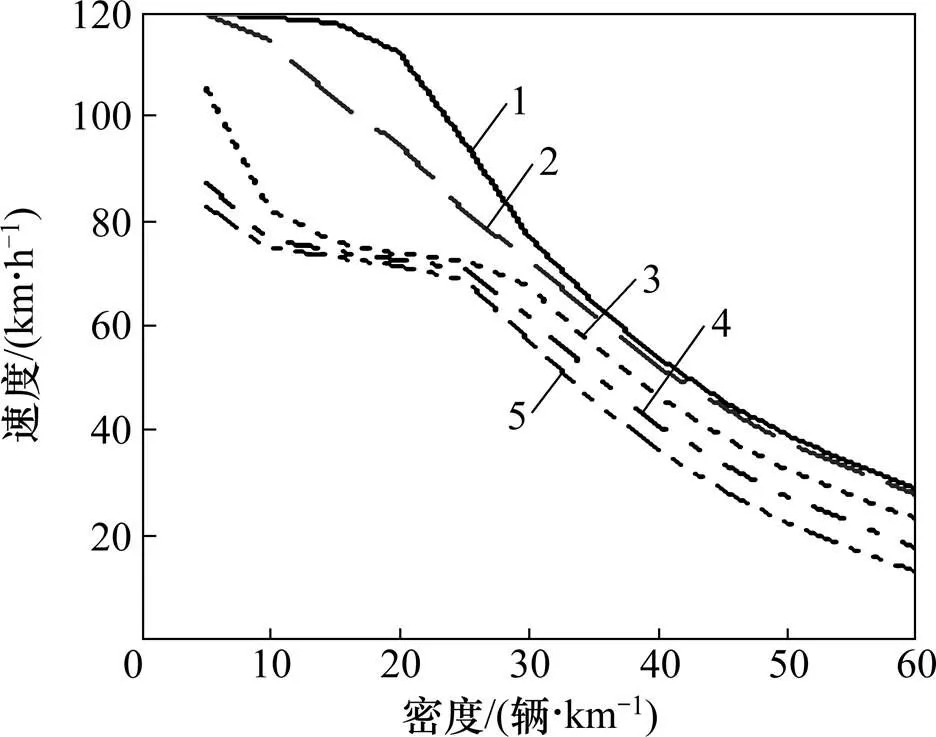
不同大货车比率下小客车速度与密度的关系见图2。从图2可见:小客车速度随增大而下降,在中低密度区下降明显,但在中密度区且≥0.25时,小客车速度变化较小。实验结果表明:在中低密度区,大货车速度不受影响;增大会同时导致快车道和慢车道速度降低。
不同大货车比率下小客车换道率与密度的关系见图3。从图3可见:混入大货车后,小客车换道率明显增大;在低密度区,越大,小客车换道率越大,这种变化在<0.25时更显著。在不同下,小客车换道率−密度曲线的变化趋势不尽相同,=0时存在双峰值,=0.05时存在单峰值,≥0.25时呈单调递减。
R:1—0;2—0.05;3—0.25;4—0.50;5—0.75。

R:1—0;2—0.05;3—0.25;4—0.50;5—0.75。
不同大货车比率下大货车的慢车道使用率与密度的关系见图4。从图4可见:大货车主要使用慢车道,但其使用率随着增大而减小,这种变化在<0.25时更显著;在不同下,大货车对慢车道的使用率在中低密度区随着密度的增大而减小,在高密度区基本不变。实验结果表明:由于大货车的影响,小客车主要使用快车道,其使用率在低密度区随着的增大而减小。
不同大货车比率下小客车冲突率与密度的关系见图5。从图5可见,对小客车冲突率影响显著,在不同下,随着密度增大,小客车冲突率先增大后减小,越大,其峰值对应密度越小。

R:1—0;2—0.05;3—0.25;4—0.50;5—0.75。
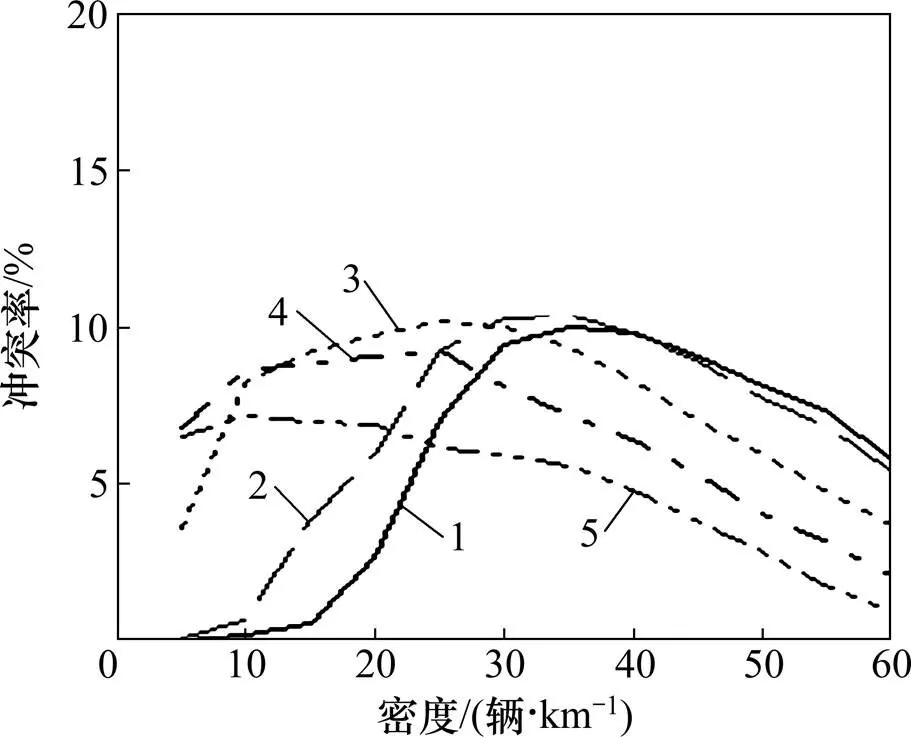
R:1—0;2—0.05;3—0.25;4—0.50;5—0.75。
图6所示为=25辆/km即临界密度附近不同下的时空斑图。斑图含义如下:竖直向上为位移方向,水平向右为时间方向,灰色代表小客车,黑色代表大货车。从图6(a)和(b)可见:在=0.05时,大货车全部在慢车道行驶,快车道不受大货车干扰。从图6(c)和(d)可见:在=0.1时,极少数大货车不时驶入驶出快车道,对快车道的小客车形成一定干扰。从图6(e)和(f)可见:在=0.25时,快车道上总有少量大货车在行驶,快车道的小客车受到严重阻碍。从图6(g)和(h)可见:在=0.5时,尽管大多数大货车使用慢车道,2条车道还是处于被大货车严重阻滞的状态。
图6还反映了2种典型的交通现象:1)移动瓶颈,表现为大货车前方出现较大空隙,是大货车占用快车道行驶随机所致;2) 偏析效应,可分为车道偏析效应和车型偏析效应,前者表现为客货车分道行驶,越小越明显,后者表现为同种车型结队行驶,越大越明显。

(a) 快车道(R=0.05);(b) 慢车道(R=0.05);(c) 快车道(R=0.1);(d) 慢车道(R=0.1);(e) 快车道(R=0.25);(f) 慢车道(R=0.25);(g) 快车道(R=0.5);(h) 慢车道(R=0.5)
3.2 大货车动力性能的影响分析
为考察大货车动力性能的影响,大货车最大速度max分别取126.0,100.8,75.6和50.4 km/h,对应的最大加速度max分别取14.0,10.5,7.0和3.5 m/s2。本文只考察大货车占比很小的情况,取0.05,其余参数取值见2.2节,实验结果及分析如下。
大货车不同最大速度max下的流量与密度的关系见图7。从图7可见:在中密度区,max对流量的影响较大,max越小,对应的最大流量越小,临界密度越大。在低密度区和高密度区,max对流量影响较小。
大货车不同最大速度max下小客车速度与密度的关系见图8。从图8可见:在中密度区,max对小客车速度的影响较大,max越小导致小客车速度越低。在低密度区和高密度区,max对小客车速度影响较小。
大货车不同最大速度max下小客车换道率与密度的关系见图9。从图9可见:随着max减小,小客车换道率明显增大,在中密度区增大最显著。实验结果表明,在中低密度区,大货车换道率随着max减小而减小。

vmax/(km∙h−1):1—126.0;2—100.8;3—75.6;4—50.4。

vmax/(km∙h−1):1—126.0;2—100.8;3—75.6;4—50.4。
大货车不同最大速度max下大货车的慢车道使用率与密度的关系见图10。从图10可见:大货车对慢车道的使用率随着max减小而增大。若大货车比小客车性能差,则当<20辆/km时,大货车几乎全部在慢车道行驶,当>20辆/km时,大货车对慢车道的使用率陡降。实验结果表明:max对小客车分布的影响主要体现在中低密度区,max越小,小客车对快车道的使用率越大。

vmax/(km∙h−1):1—126.0;2—100.8;3—75.6;4—50.4。

vmax/(km∙h−1):1—126.0;2—100.8;3—75.6;4—50.4。
大货车不同最大速度下小客车冲突率与密度的关系见图11。从图11可见:小客车冲突率在中密度区随着max影响较大,在低密度和高密度区受max影响较小;随着密度增大,小客车冲突率先增大后减小,峰值出现在临界密度附近。

vmax/(km∙h−1):1—126.0;2—100.8;3—75.6;4—50.4。
4 结论
1)本文对换道的分类和对法定换道规则的描述是合理的,建立的元胞自动机模型能反映现实交通的关键特性和现象,表明模型是有效的。
2) 大货车比率对交通运行影响显著。大货车比率越大,会导致大货车对快车道的占用越多,小客车速度越,低密度区小客车的换道和冲突越多。上述变化在大货车比率小于0.25时更显著,并与密度相关。
3) 当大货车比率很小时,大货车动力性能对交通运行也有显著影响。大货车动力性能越差,虽然大货车对快车道的占用越少,但还是会导致小客车速度越低,换道和冲突越多。上述变化在中密度区最显著。
4) 在临界密度附近,随着大货车比率变化,可随机观察到典型的移动瓶颈、车道偏析效应和车型偏析效应。上述现象还有待进一步实证和定量研究。
[1] 王殿海, 金盛. 车辆跟驰行为建模的回顾与展望[J]. 中国公路学报, 2012, 25(1): 115−127. WANG Dianhai, JIN Sheng. Review and outlook of modeling of car following behavior[J]. China Journal of Highway and Transport, 2012, 25(1): 115−127.
[2] 贾宁, 马寿峰. 最优速度模型与元胞自动机模型的比较研究[J]. 物理学报, 2010, 59(2): 832−841. JIA Ning, MA Shoufeng. Comparison between the optimal velocity model and the Nagel-Schreckenberg model[J]. Acta Physica Sinica, 2010, 59(2): 832−841.
[3] WOLFRAM S. Statistical mechanics of cellular automata[J]. Reviews of Modern Physics, 1983, 55(3): 601−644.
[4] NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J]. Journal of Physics I, 1992, 2(12): 2221−2229.
[5] CHOWDHURY D, SANTEN L, SCHADSCHNEIDER A. Statistical physics of vehicular traffic and some related systems[J]. Physics Reports, 2000, 329(4): 199−329.
[6] RICKERT M, NAGEL K, SCHRECKENBERG M, et al. Two lane traffic simulations using cellular automata[J]. Physica A: Statistical Mechanics and its Applications, 1996, 231(4): 534−550.
[7] CHOWDHURY D, WOLF D E, SCHRECKENBERG M. Particle hopping models for two-lane traffic with two kinds of vehicles: effects of lane-changing rules[J]. Physica A: Statistical Mechanics and its Applications, 1997, 235(3): 417−439.
[8] NAGEL K, WOLF D E, WAGNER P, et al. Two-lane traffic rules for cellular automata: A systematic approach[J]. Physical Review E, 1998, 58(2): 1425−1437.
[9] 杨柳, 黄中祥, 况爱武. 换道规则对高速公路双车道交通流的影响[J]. 中南大学学报(自然科学版), 2016, 47(5): 1752−1759.YANG Liu, HUANG ZHongxiang, KUANG Aiwu. Influence of lane-changing rules on two-lane traffic flow of freeway[J]. Journal of Central South University (Science and Technology), 2016, 47(5): 1752−1759.
[10] 史峰, 周文梁, 刘芬芳, 等. 基于元胞自动机的双车道环岛交通流特性研究[J]. 中南大学学报(自然科学版), 2010, 41(4): 1616−1622. SHI Feng, ZHOU Wenliang, LIU Fenfang, et al. Two-lane roundabout traffic flow characteristics based on cellular automaton[J]. Journal of Central South University (Science and Technology), 2010, 41(4): 1616−1622.
[11] 敬明, 邓卫, 王昊, 等. 基于跟车行为的双车道交通流元胞自动机模型[J]. 物理学报, 2012, 61(24): 331−339. JING Ming, DENG Wei, WANG Hao, et al. Two-lane cellular automaton traffic model based on car following behavior[J]. Acta Physica Sinica, 2012, 61(24): 331−339.
[12] 敬明, 邓卫, 季彦婕, 等. 更新步长和元胞尺寸对元胞自动机模型的影响[J]. 吉林大学学报(工学版), 2013, 43(2): 310−316. JING Ming, DENG Wei, JI Yanjie, et al. Influences of time step and cell size on cellular automaton model[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(2): 310−316.
[13] 钟连德, 孙小端.高速公路安全与交通流特征参数关系[J]. 北京工业大学学报, 2013, 39(2): 251−256.ZHONG Liande, SUN Xiaoduan. Relationship between traffic flow and safety on freeway[J]. Journal of Beijing University of Technology, 2013, 39(2): 251−256.
[14] 梁国华, 程国柱, 王春艳, 等. 高速公路大型车混入率与交通流稳定性关系[J]. 长安大学学报(自然科学版), 2014, 34(4): 120−126.LIANG Guohua, CHENG Guozhu, WANG Chunyan, et al. Relationship between mixing rate of freeway large vehicles and traffic flow stability[J]. Journal of Chang’an University (Natural Science Edition), 2014, 34(4): 120−126.
[15] 刘有军, 李可, 余俊, 等.四车道高速公路跟驰换道模型与参数激励[J]. 中国公路学报, 2014, 27(12): 96−105.LIU Youjun, LI Ke, YU Jun, et al. Car-following and lane-changing modeling and parametric excitation on four-lane expressway[J]. China Journal of Highway and Transport, 2014, 27(12): 96−105.
[16] 肖瑞杰, 孔令江, 刘慕仁.车辆的长度和速度对单车道混合交通流的影响[J]. 物理学报, 2007, 56(2): 740−746.XIAO Ruijie, KONG Lingjiang, LIU Muren. The influence of the length and the velocity of vehicles on the mixed traffic flow in one-lane highway[J]. Acta Physica Sinica, 2007, 56(2): 740−746.
[17] 潘卫军, 杨凯.车辆长度和速度对双车道交通流的影响[J]. 西南交通大学学报, 2013, 48(2): 335−342.PAN Weijun, YANG Kai. Influence of vehicle length and velocity on mixed traffic flow in two-Lane traffic flow[J]. Journal of Southwest Jiaotong University, 2013, 48(2): 335−342.
[18] 付强, 杨晓芳, 王建蓉.低速货车影响下不同类型驾驶员的跟车行为[J]. 公路交通科技, 2013, 30(9): 134−139.FU Qiang, YANG Xiaofang, WANG Jianrong. Car-following behaviors of different types of driver under low-speed truck impact[J]. Journal of Highway and Transportation Research and Development, 2013, 30(9): 134−139.
[19] 冯树民, 聂涔, 胡宝雨. 基于元胞自动机的高速公路货车结伴行为研究[J]. 交通运输系统工程与信息, 2016, 16(5): 97−103.FENG Shumin, NIE Cen, HU Baoyu. Partnering behavior of truck platoon on freeway based on cellular automaton[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(5): 97−103.
[20] 柴华, 周荣贵, 谢军. 基于公路运行速度设计的标准车型分类标准[J]. 中国公路学报, 2010, 23(S1): 13−18.CHAI Hua, ZHOU Ronggui, XIE Jun. Standard vehicle type classification criteria based on highway operating speed design[J]. China Journal of Highway and Transport, 2010, 23(S1): 13−18.
(编辑 陈灿华)
Modeling with cellular automata and influence analysis of trucks on freeway traffic flow
YANG Liu, LONG Kejun, HUANG Zhongxiang
(Key Laboratory of Highway Engineering of Ministry of Education,Changsha University of Science & Technology, Changsha 410114, China)
Based on the analysis of traffic characteristics of four-lane freeways in China, lane-changing types were classified into tendentious and non-tendentious ones according to the motivation, and the legal lane-changing rules were described concisely. The corresponding cellular automaton model was proposed, which was calibrated and verified with the measured traffic flow parameters. The results show that, with the increase of the truck ratio, the fast lane occupation by trucks increases and the speed of cars decreases. The above changes are more significant when the truck ratio is less than 0.25 and is correlated with the density. When the truck ratio is very small, as the truck power performance degrades, the speed of cars decreases and the lane-changing rate and conflict rate of cars increase. The above changes are most significant when the density is in the medium range. When it is near the critical density, the typical moving bottlenecks and segregation effects can be observed at random when the truck ratio changes.
four-lane freeway; two-lane traffic flow; truck; lane-changing rule; cellular automata; simulation
10.11817/j.issn.1672−7207.2017.10.033
U491.1+12;U491.2+6
A
1672−7207(2017)10−2800−08
2016−10−12;
修回日期:2016−12−23
国家自然科学基金资助项目(51338002,51678076,51408058);湖南省教育厅资助项目(16B008);长沙理工大学公路工程教育部重点实验室开放基金资助项目(KFJ130101)(Projects(51338002, 51678076, 51408058) supported by the National Natural Science Foundation of China; Project(16B008) supported by Education Department of Hunan Province; Project(KFJ130101) supported by Open Fund of the Key Laboratory of Highway Engineering of Ministry of Education, Changsha University of Science & Technology)
杨柳,博士,讲师,从事交通流和公路市政CAD研究;E-mail:yangliuemail@163.com

