考虑风电与负荷时序性的分布式风电源选址定容

初 壮，乔福泉

（东北电力大学电气工程学院，吉林 132012）

考虑风电与负荷时序性的分布式风电源选址定容

初 壮，乔福泉

（东北电力大学电气工程学院，吉林 132012）

配电网中分布式风电源选址定容时，计及风电机组出力和节点负荷的时序性特征。利用蒙特卡洛模拟MCS（Monte Carlo simulation）对一年内每小时风速进行抽样，并求出对应的风机出力。综合考虑每小时风机出力效率以及对应的节点小时负荷负载率，构建小时场景，利用改进K-means聚类法进行场景聚类。根据聚类后每个场景的风机出力效率均值、负荷负载率均值以及对应场景的概率，以配电公司最小年费用成本为目标函数，利用改进遗传算法对分布式风电源进行选址定容。对33节点算例的仿真分析结果表明，风机出力与节点负荷的时序特性对分布式风电源的选址定容有重大影响，同时也验证了所提模型及方法的有效性。

分布式风电源；时序性；场景；改进K-means聚类法

随着能源危机、环境危机逐渐加剧，分布式电源，尤其是以风电为代表的可再生能源类型的分布式电源越来越受到重视。分布式风电源DWG（distributed wind generation）具有灵活、环保等优点，通常靠近用户侧安装。一般而言，DWG的接入能减少配电线路上的功率流动，从而使网络损耗降低、节点电压质量得到改善[1-3]，配电网运行水平得到提高，而运行水平的提高程度则与DWG的位置与容量具有直接关系[4]。文献[5]研究了在不考虑负荷新增节点情况下，以配电网网损费用等为目标的分布式电源规划。文献[6]则建立了以配电网污染气体排放量、总费用和系统电压偏差为目标的多目标分布式电源选址定容优化配置模型。文献[7]提出了旨在解决电力市场环境下进行多种分布式电源的选址、定容和技术组合问题的静态模糊多目标模型。

然而，DWG、光伏发电等出力具有随机性、波动性，它们对降低网损等提高电网运行水平的影响程度不但与其位置和容量有关，还与它们时序特性有关。随着配电网中DWG渗透率越来越高，DWG的时序特性对配电网运行水平的影响也会越来越大。文献[8]考虑了风电机组出力的随机性以及负荷的不确定性，将机会约束规划应用到DWG的选址定容中。文献[9]采用场景构建法来处理不确定性因素，但其场景是主观划分的。文献[10-11]中考虑了分布式电源以及负荷的时序特性，选择春夏秋冬四季的典型日进行分析，不能全面反映一年内的时序特性。

分布式电源选址定容问题的特点决定了其数学模型是一个整数规划模型。关于模型的求解，学者们已经提出一些比较有效的方法。文献[5]提出一种自适应变异粒子群算法AMPSO（adaptive mutation of particle swarm optimization），对分布式电源进行优化规划，克服了粒子群算法易早熟的问题；文献[6]采用非线性变异操作避免了粒子群算法陷入局部最优，扩大了粒子的搜索空间；文献[9-11]则采用遗传算法对规划模型进行求解，并对遗传算法采取了不同的改进措施。

本文研究了考虑配电网DWG出力与负荷水平全年时序特性的分布式风电源的选址定容问题。根据每小时风机出力效率以及对应的节点小时负荷负载率，构建小时场景，利用改进K-means聚类法进行场景聚类。以配电网公司最小年费用成本为目标函数，利用改进遗传算法对建立的数学模型进行求解。

1 时序性建模及场景构建

1.1 风速的概率分布及风机出力

风机出力主要受风速的影响，一般认为，风速的概率分布满足2参数的Weibull分布，其概率密度函数和分布函数[12]分别为

式中：v为风机叶轮轮毂处的风速；e和c分别为Weibull分布的形状参数和尺度参数；V为给定风速，m/s。给定分布参数e和c后，风能特征即可确定。

风机有功出力与风速的关系可近似表示为

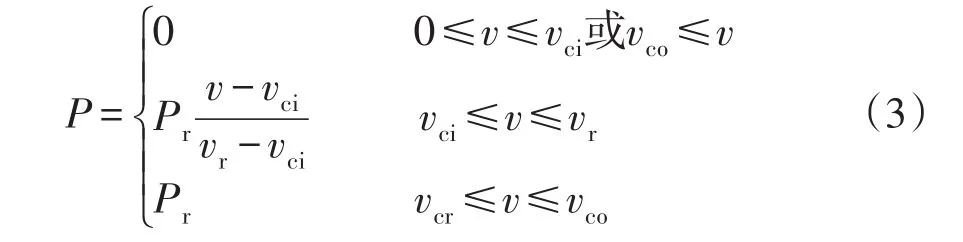
式中：Pr为风机的额定功率；vci、vr和vco分别为风机的切入风速、额定风速和切出风速。

1.2 年时序负荷

分析待规划区域节点负荷的历史数据，以小时为单位，得到各个负荷节点的年时序负荷负载率曲线。

1.3 场景构建

（1）根据风速概率分布模型，利用蒙特卡洛模拟MCS（Monte Carlo simulation）对每小时风速进行抽样，得到年时序风速曲线。由于风能特征主要与分布参数e、c有关，考虑到某地区风速在不同时段分布情况不尽相同，因此，本文在模拟风速时，不同月份采用不同的e、c值。

（2）由风机有功出力与风速的关系，即得风机有功出力时序曲线。

（3）根据风机有功出力时序曲线与负荷时序曲线，得到对应的风机出力效率PDWG曲线与负载率PL曲线，可得PDWG－PL小时场景。

（4）利用改进K-means聚类法对小时场景聚类，聚类后得到K个场景。

1.4 基于改进K-means聚类法的场景聚类

K-means聚类是著名的划分聚类算法，算法的基本步骤如下[13]。

步骤1设定聚类个数K，并从n个数据中随机选择K个样本作为初始聚类中心Zk（k=1，2，…，K）。

步骤2根据聚类中心计算每个对象Xi（i=1，2，…，n）到各个聚类中心的距离，根据最小距离原则进行划分类别。

步骤3计算新的聚类中心，即

式中：Ck为第k类所有对象；Nk为第k类包含的对象数。

步骤4重复步骤2和步骤3，直到分类不再变化。

可以看出，原始的K-means聚类法需要事先人为设定聚类的个数，并且其初始聚类中心是随机产生的，容易使结果陷入局部最优。而文献[14]根据Sturges经验公式来确定聚类数K，并利用层次聚类法得到K-means聚类的初始聚类中心，然后进行聚类。

人为或采用经验公式确定聚类数K不可避免地带有一定主观性。为了降低此种影响，本文采用遗传算法与K-means相结合的方法[15]，利用遗传算法的全局搜索特性来自主获取K值，并根据X的范围，均匀地随机生成初始聚类中心。在聚类计算过程中，聚类的个数K与聚类中心的位置都是优化变量，以改善聚类结果的合理性。结合本文问题，聚类主要工作内容阐述如下。

（1）采用二进制编码，每个个体代表一种聚类数K。

（2）根据每个个体对应的K值以及生成的初始聚类中心进行聚类。适应度函数为

式中：EK为某一类个体中，所有个体到该类质心的距离之和；DK为K个质心之间距离的最大值。

（3）选择、交叉、变异操作，产生下一代种群。

（4）遗传算法终止条件：①达到最优解连续不变最大代数；②达到遗传算法的最大迭代次数；③为第g代最优个体的目标函数，Fg-1为第g－1代最优个体的目标函数。

2 DWG选址定容的数学模型建立

2.1 数学模型中场景数量的选取

通过聚类分析，得到配电网系统的年时序特性可以聚类为K个场景。建模所面临的问题是，优化模型中是否应该计入所有K个场景。一方面，如果计入所有场景，部分场景出现的概率较低，但这些场景对应的约束条件对优化计算过程一直产生影响，使DWG选址定容优化的可行空间变小。另一方面，如果不计入部分场景，则优化结果对应的DWG的位置和容量在这些不计入场景投入运行可能出现潮流越限等不满足运行约束的情况。不过，考虑到DWG运行时可以“弃风”，第2个问题可以通过“弃风”使运行约束得到满足。

因此，为使DWG尽可能达到最优配置，提高配电系统的整体效益，优化模型中的场景数不一定要取总场景数。记选址定容优化计算中用到的场景数为K′，它与聚类计算所得的聚类数亦即总场景数K之间的关系为

在以下研究中，本文考虑将场景按照出现概率进行排序，分别选取不同的K′个概率相对较大的场景进行分析，求出K′个场景下DWG的选址定容结果，再将该选址定容方案代入全场景情况下配电系统效益函数计算全年费用，进而比较分析选取不同K′情况下的优化结果及相应全场景运行费用。选取全场景运行费用最小对应的优化结果配置DWG。因为总场景数较小，采用上述“枚举”K′的方法是可行的。

2.2 目标函数

以配电系统K′个场景下费用最小构造目标函数，这一费用为K′个场景下网络有功损耗费用、由上级电网购买的有功费用、DWG的投资及运行维护年费用之和减掉引入DWG所带来的环境收益，即

式中：ΔPk为场景k下的网络有功损耗；Ptrans,k为场景k下的由上级电网购买的有功；PDWG,k为场景k下的DWG发出的有功；f（k）为场景k出现的概率；CD，total为风机总的固定投资；α为风机固定投资年平均费用系数，为折现率，n为风机使用年限；T为一年内小时数；Cp为电网电价；CpD为DWG的运行维护成本，元/（MW·h）；Cu为传统火电单位发电量的环境成本。

2.3 约束条件

（1）潮流方程约束为

式中：k=1,2,…,K′；PGi，k、QGi，k分别为场景k下节点i的有功和无功电源注入量；PLi，k、QLi，k分别为场景k下节点i的有功和无功负荷；Ui，k为场景k下节点i的电压幅值。

（2）线路功率潮流约束为

式中：Pi，k为场景k下线路i流过的有功功率；Pi，max为线路i的最大允许有功功率。

（3）分布式风电源容量约束为

式中：Pi，D为节点i处的 DWG 容量；Pi，Dmax为节点i处允许接入的DWG容量上限；PD，total为配电网中接入DWG的总容量；λ为允许接入分布式电源的最高比例；PL，total为配电网总的额定功率。

3 利用改进遗传算法对DWG进行选址定容

本文采用一种改进遗传算法求解场景数为K′时式（6）～式（9）构成的优化数学模型。

3.1 染色体编码

本文采用十进制整数编码，X={X1，X2，…，Xm}，每条染色体代表一种规划方案，染色体的长度定义为允许接入分布式风电源的节点数，染色体上每位基因的大小代表对应节点接入DWG的台数，即代表接入DWG的容量。

3.2 遗传算子

选择算子时采用精英保留策略，即将前一代个体中适应度最高的几个个体直接遗传给下一代。交叉、变异算子中采用自适应交叉、变异概率[16-17]。

3.3 求解步骤

求解的主要步骤如下。

步骤1根据第1节中方法建立小时场景，然后利用改进K-means法进行聚类，得到K个场景，并按出现的概率排序。

步骤2取K′个场景，利用改进遗传算法进行DWG选址定容优化计算，求出此时的DWG的选址定容结果；然后，在该DWG配置情况下，计算计入全部K个场景情况的全场景运行费用。在计算全场景运行费用时，DWG按照时序特性发电很有可能出现不满足在优化配置中没有计及的K-K′个场景的约束条件式（9），即DWG的发电功率越限。在这些越限场景下，DWG的发电功率取为约束条件决定的功率上限，对应的是DWG出现弃风的情况。

步骤3对比分析不同K′值时，DWG的选址定容结果、目标函数值与全场景运行费用值。DWG选址定容的完整计算流程如图1所示。

图1 求解算法流程Fig.1 Solving process of algorithm

4 算例分析

本文通过IEEE 33节点配电系统（如图2所示）对所提模型及方法进行验证，配电网参数参考文献[18]，系统电压等级12.66 kV，其中节点6、7、23、24、25、26、27、29、31、32允许DWG接入。DWG的总装机容量不超过总额定负荷功率的30%，单个DWG容量为50 kW，切入风速、切出风速、额定风速分别为3.5 m/s、25 m/s、9.5 m/s。

图2 33节点配电网Fig.2 33-node distribution network

考虑到不同时间段风速分布特征不同，本文中不同月份采用不同的e、c值[19]。假定一年有8 760个小时，最后24 h的负载率采用第1天的值，负荷负载率见文献[20]。风速及负荷负载率年时序曲线如图3所示。

图3 风速及负载率年时序曲线Fig.3 Annual timing curves of wind speed and loading rate

根据风速曲线得到对应的风机出力效率曲线，再结合负载率年时序曲线，即可得到PDWG－PL小时场景。利用改进K-means聚类算法对小时场景进行聚类，聚类后得到28个场景，聚类结果见表1。

考虑到有些场景的概率相对较低，选取不同K′个场景进行对比分析。由表1看出相邻场景的概率相差并不大，因此，本文选择K′=4，8，12，16，20，24，28。不同K′值下的DWG选址定容结果以及总成本如表2和表3所示。

由表2和表3可以看出，不同K′值下的DWG选址定容结果以及全场景运行费用有一定区别。

（1）从目标函数值看，考虑单一场景情况时，目标函数在满足约束条件下取得的值最小，随着场景数的增加，目标函数值在下降。这是因为考虑的场景数越多，问题的约束条件越多，问题的可行域越小，数量较少场景下的优化方案在数量较多场景下变成了不可行方案。

表1 聚类结果Tab.1 Clustering results

表2 不同K′值下的DWG选址定容结果Tab.2 Result of DWG’s locating and sizing with different values ofK′

表3 不同K′值下的优化目标函数值与全场景运行费用对比Tab.3 Comparison between objective function values with different values ofK′and their operation costs in all scenarios万元

（2）从全场景运行费用看，随着优化计算考虑的场景数逐渐增加，全场景运行费用的变化趋势是先减小、再增大。这一情况说明，在场景数较少时，约束条件较少，DWG的安装量较多，系统网损下降与环境效益增加产生的收益高于DWG的安装成本；而在考虑场景数较多时，DWG安装数量很少，对网损下降与环境效益增加影响都不大，所以在场景数多于一定数量之后，优化时考虑更多的场景数，全场景运行费用变化也不大。

可见，优化计算考虑过多的场景数会使优化空间变小，从而影响配电系统实际运行时的效益；优化时考虑单一场景（或较少场景），如果这些场景负荷较低，则接入DWG对降低网损、提高环境效益影响都不大，使得DWG成本成为影响目标函数值的主要因素，从而使DWG接入数量较少，而全场景运行费用下降也较少。根据表3中的结果，本文选择K′=8时的DWG选址定容方案。

此外，在不考虑负荷与风电时序性的情况下对DWG进行选址定容，并将结果代入本文K′=8的情况下（考虑时序性）进行对比分析，结果如表4所示。

表4 DWG的选址定容结果及总成本对比Tab.4 Comparison between results of DWG’s locating，sizing and total costs

由表4中的结果对比可以看出，不考虑时序性时DWG的接入容量有所增加，然而电网总成本却增加很多，主要是由于弃风情况比较严重，风电利用率较低，进一步说明了本文中DWG选址定容时考虑DWG与负荷的年时序特性的必要性、合理性。

5 结 语

本文在对分布式风电源选址定容时，充分考虑了风速及节点负荷的时序变化这一特征，规划结果更接近实际情况。根据风速及负荷特征建立小时场景，并采用改进K-means聚类法对小时场景进行聚类，可以有效减少场景数量，提高模拟、求解速度。对比分析了选取部分概率相对较大的场景后，分布式风电源的接入情况，从而得到尽可能好的分布式风电源的配置结果。通过比较考虑分布式风电源及负荷的年时序特性，与不考虑二者时序性的选址定容结果，可以看出，二者的年时序特性对分布式风电源的选址定容有重要影响。

[1]王志群，朱守真，周双喜，等（Wang Zhiqun，Zhu Shouzhen，Zhou Shuangxi，et al）.分布式发电对配电网电压分布的影响（Impact of distributed generation on the distribution system voltage profile）[J].电力系统自动化（Automation of Electric Power Systems），2004，28（16）：56-60．

[2]Borges C L T，Falcao D M.Impact of distributed generation allocation and sizing on reliability，losses and voltage profile[C]//IEEE Power Technology Conference，Bologna（Italy），2003．

[3]于建成，迟福建，徐科，等（Yu Jiancheng，Chi Fujian，Xu Ke，et al）.分布式电源接入对电网的影响分析（Analysis of the impact of distributed feneration on power grid）[J].电力系统自动化学报（Proceedings of the CSU-EPSA），2012，24（1）：138-141．

[4]胡骅，吴汕，夏翔，等（Hu Hua，Wu Shan，Xia Xiang，et al）.考虑电压调整约束的多个分布式电源准入功率计算（Computing the maximum penetration level of multiple distributed generators in distribution network taking into account voltage regulation constraints）[J].中国电机工程学报（Proceedings of the CSEE），2006，26（19）：13-17．

[5]叶德意，何正友，臧天磊（Ye Deyi，He Zhengyou，Zang Tianlei）.基于自适应变异粒子群算法的分布式电源选址与容量确定（Siting and sizing of distributed generation planning based on adaptive mutation particle swarm optimization algorithm）[J].电网技术（Power System Technology），2011，35（6）：155-160．

[6]栗然，申雪，钟超，等（Li Ran，Shen Xue，Zhong Chao，et al）.考虑环境效益的分布式电源多目标规（Multi-objective planning of distributed generation considering environmental benefit）[J].电网技术（Power System Technology），2014，38（6）：1471-1478．

[7]曾鸣，杜楠，张鲲，等（Zeng Ming，Du Nan，Zhang Kun，et al）.基于多目标静态模糊模型的分布式电源规划（Distributed generation planning based on multiobjective static fuzzy model）[J].电网技术（Power System Technology），2013，37（4）：954-959．

[8]张节潭，程浩忠，姚良忠，等（Zhang Jietan，Cheng Haozhong，Yao Liangzhong，et al）.分布式风电源选址定容规划研究（Study on siting and sizing of distributed wind generation）[J].中国电机工程学报（Proceedings of the CSEE），2009，29（16）：1-7．

[9]Martins V F，Borges C L T.Active distribution network integrated planning incorporating distributed generation and load response uncertainties[J].IEEE Transactions on Power Systems，2011，26（4）：2164-2172．

[10]李亮，唐巍，白牧可，等（Li Liang，Tang Wei，Bai Muke，et al）.考虑时序特性的多目标分布式电源选址定容规划（Multi-objective locating and sizing of distributed generators based on time-sequence characteristics）[J].电力系统自动化（Automation of Electric Power Systems），2013，37（3）：58-63，128．

[11]徐迅，程浩忠，倪炜，等（Xu Xun，Cheng Haozhong，Ni Wei，et al）.考虑环境成本和时序特性的微网多类型分布式电源选址定容规划（Optimal site selection and capacity determination of multi-types of distributed generation in microgrid considering environment cost and timing characteristics）[J].电网技术（Power System Technology），2013，37（4）：914-921．

[12]丁明，吴义纯，张立军（Ding Ming，Wu Yichun，Zhang Lijun）.风电场风速概率分布参数计算方法的研究（Study on the probabilistic distribution parameters of wind speed in wind farms）[J].中国电机工程学报（Proceedings of the CSEE），2005，25（10）：107-110．

[13]毛国君.数据挖掘原理与算法[M].北京：清华大学出版社，2005．

[14]陈凡，刘海涛，黄正，等（Chen Fan，Liu Haitao，Huang Zheng，et al）.基于改进k-均值聚类的负荷概率模型（Probabilistic load model based on improvedk-means clustering algorithm）[J].电力系统保护与控制（Power System Protection and Control），2013，41（22）：128-133．

[15]刘婷，郭海湘，诸克军，等（Ling Ting，Guo Haixiang，Zhu Kejun，et al）.一种改进的遗传k-means聚类算法（An improved genetick-means algorithm for optimal clustering）[J].数学的实践与认识（Mathematics in Practice and Theory），2007，37（8）：104-111．

[16]兰华，王伟，王韵然，等（Lan Hua，Wang Wei，Wang Yunran，et al）.基于小生境遗传算法的风光互补发电系统配置优化（Configuration optimization of wind/photovoltaic hybrid power systems based on niche genetic algorithms）[J].东北电力大学学报（Journal of Northeast Dianli University），2010，30（4）：31-35．

[17]张国强，彭晓明（Zhang Guoqiang，Peng Xiaoming）.自适应遗传算法的改进与应用（Improvement and application of an improved adaptive genetic algorithm）[J].船舰电子工程（Ship Electronic Engineering），2010，187（1）：83-84．

[18]麻秀范（Ma Xiufan）.含分布式电源的配电网规划与优化运行研究（Research on Planning and Optional Operation of Distribution Network Including Decentralized Generation）[D].北京：华北电力大学电气与电子工程学院（Beijing：School of Electrical and Electronic Engineering，North China Electric Power University），2013．

[19]龚伟俊，李为相，张广明（Gong Weijun，Li Weixiang，Zhang Guangming）.基于威布尔分布的风速概率分布参数估计方法（The estimation algorithm on the probabilistic distribution parameters of wind speed based on Weibull distribution）[J].可再生能源（Renewable Energy Resources），2011，29（6）：20-23．

[20]邵黎（Shao Li）.计及负荷变化的配电网可靠性评估模型与算法研究（Study on Model and Algorithm for Electrical Distribution Network Reliability Considering the Load Changing）[D].重庆：重庆大学电气工程学院（Chongqing：College of Electrical Engineering，Chongqing University），2007．

Locating and Sizing of Distributed Wind Generation Considering Wind Generation and the Timing Characteristics of Load

CHU Zhuang，QIAO Fuquan
（School of Electrical Engineering，Northeast Electric Power University，Jilin 132012，China）

In this paper，the timing characteristics of wind turbine output and node loads are considered during the locating and sizing of distributed wind generation（DWG）in distribution network.The hourly wind speeds in one year are sampled using Monte Carlo simulation（MCS），and the corresponding wind turbine output is obtained.Then，hourly scenarios are constructed considering both the hourly output efficiency of the wind turbine and the corresponding hourly loading rate at nodes，and an improvedK-means clustering algorithm is used to perform scenario clustering.According to the clustering results，which include the average of wind turbine output efficiencies，the average of loading rates，as well as the probability of the corresponding scenario，an improved genetic algorithm is employed to locate and size the DWG with the minimum annual cost of a distribution company as an objective function.The simulation results of a 33-node distribution network show that the timing characteristics of wind turbine output and node loads have a significant impact on the locating and sizing of DWG.Meanwhile，the effectiveness of the proposed model and method is verified.

distributed wind generation（DWG）；timing characteristic；scenario；improvedK-means clustering algorithm

TM715

A

1003-8930（2017）10-0085-06

10.3969/j.issn.1003-8930.2017.10.015

2015-10-12；

2017-03-15

初 壮（1973—），男，博士，副教授，研究方向为电力系统优化运行。Email：chuzhuang@hotmail.com

乔福泉（1990—），男，硕士研究生，研究方向为含分布式电源的配电网规划。Email：qiaofuquan007@163.com